Graebel W.P. Advanced Fluid Mechanics
Подождите немного. Документ загружается.


134 Surface and Interfacial Waves
The constants of integration can be evaluated by noting that at both the crests and
the troughs of the waves the slope is zero. Thus,
2
=
3 −h
trough
h
crest
− −L
h
crest
h
trough
L
where L =
2C
g
−h
crest
+h
trough
and L ≤h
trough
≤ ≤ h
crest
(4.7.8)
The magnitude restriction on L comes about because the right-hand side must always
be positive to match the left-hand side.
Applying the conditions at the crest and trough of the waves, the constants D and
H are found to be given by
D
2
=gLh
trough
h
crest
H=−
h
trough
+h
crest
h
trough
h
crest
−
1
L
(4.7.9)
The solution can be advanced further by letting = h
trough
+h
crest
−h
trough
cos
2
.
Then the equation for the displacement becomes
d
dx
2
=
3h
crest
−L
h
crest
h
trough
L
1−
h
crest
−h
trough
h
crest
−L
sin
2
This can be integrated to give x as a function of and also the wavelength. The result is
x =
0
dp
1−k
2
sin
2
p
=Fk (4.7.10)
where =wavelength = 2
/2
0
dp
1−k
2
sin
2
p
=2Fk/2
and k
2
=
h
crest
−h
trough
h
crest
−L
and =
h
crest
h
trough
L
3h
crest
−L
Here, x is measured from the wave crest, and Fk is the incomplete elliptic function
of the first kind. (When = /2, it becomes the complete elliptic integral of the first
kind.) The function that is essentially the inverse of F, giving ! as a function of x,is
=h
trough
+h
crest
−h
trough
cn
2
x
(4.7.11)
where cnx/ = cos is called the cnoidal function, and the wave described by
equation (4.7.11) is the cnoidal wave.
The remaining task is to determine the constant C. From equation (4.7.1) it is seen
that C can be expressed in the form C =c
2
/2+gh, where h is the average depth and c is
the speed necessary to hold the wave steady. The amount of fluid in one wavelength is
h =
0
dx =
/2
0
dx
dp
dp = 2
/2
0
h
crest
−h
crest
−h
trough
sin
2
p
1−k
2
sin
2
p
dp
4.7 Shallow-Depth Free Surface Waves—Cnoidal and Solitary Waves 135
or
h =2
LFk/2 +h
crest
−LEk/2
/ (4.7.12)
where Ek/2 =
/2
0
1−k
2
sin
2
pdp is the complete elliptic integral of the sec-
ond kind.
The procedure for completing the solution for a specific case is as follows. First,
choose three of the variables—say, h
trough
h
crest
, and L—since their relative magnitudes
are known. From equation (4.7.10) and (4.7.12) k can be found, as well as x as a function
of the local wave elevation. Since C = c
2
/2 +gh, it follows from equation (4.7.8) that
c =
gL +h
trough
+h
crest
−h. Thus, all of the parameters of the problem have been
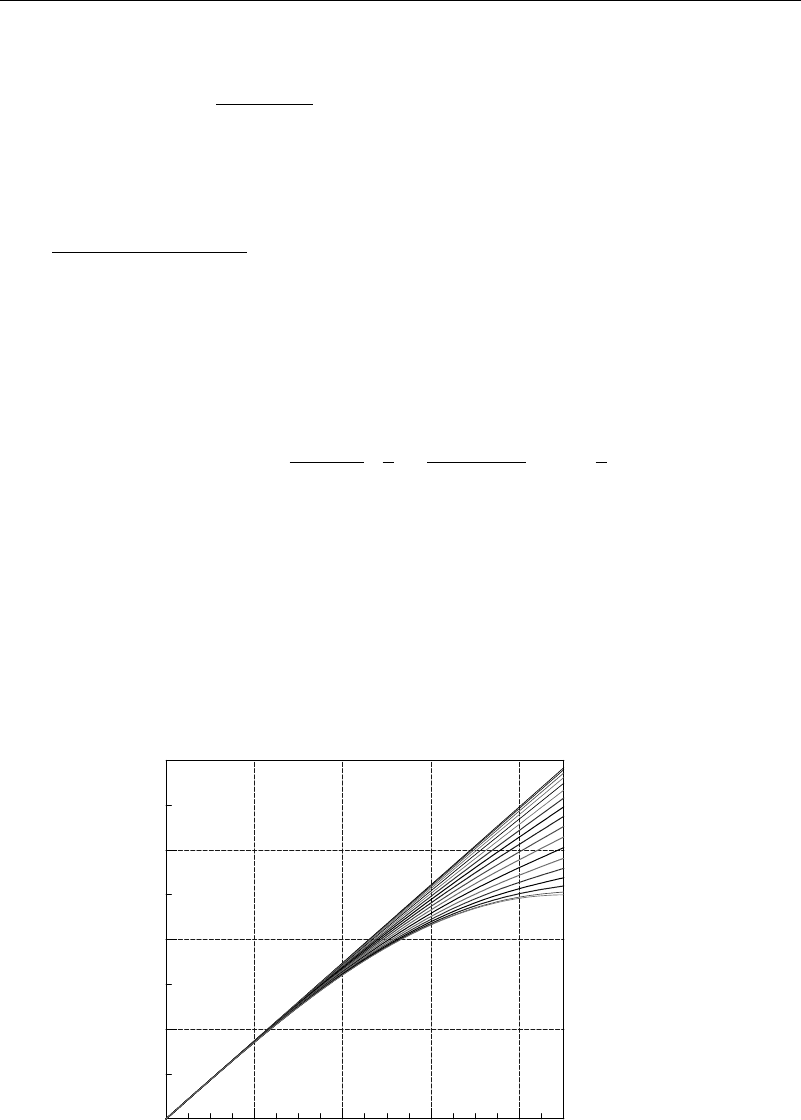
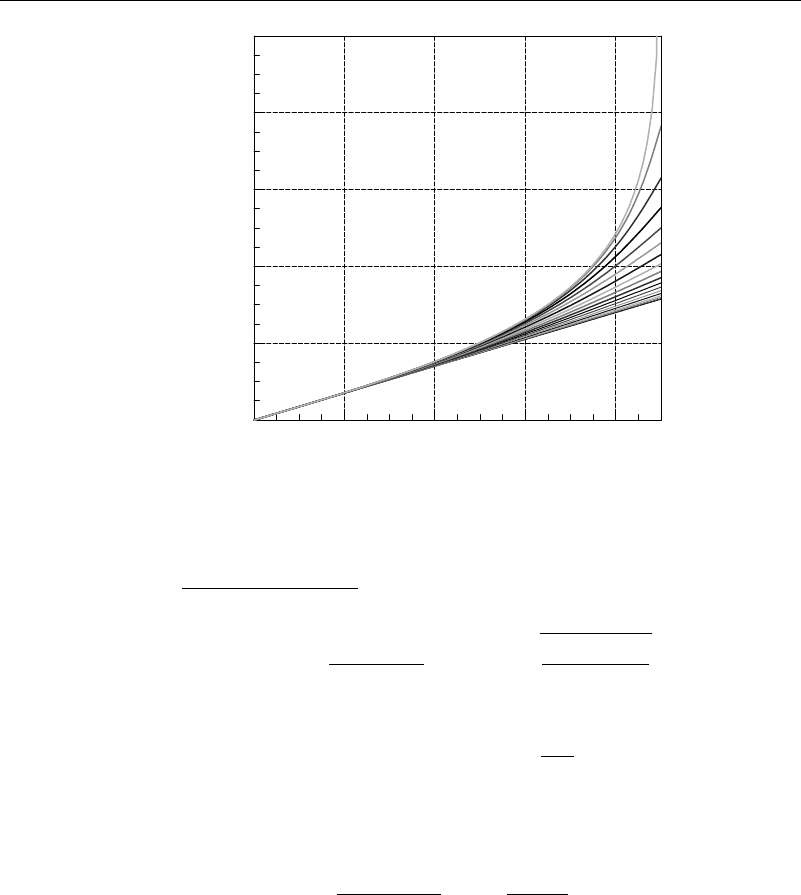
determined. Plots of the elliptic functions are given in Figures 4.7.1 and 4.7.2, where
=sin
−1
k is expressed in degrees. Values of these functions are shown in tables in the
Appendix.
A more elaborate presentation of this material is given in Wehausen and Laitone
(1960, §31). Their procedure is to make x dimensionless using the wavelength x/ and
y dimensionless by a representative depth h y/h and then writing equation (4.7.2) as
x y = Gx/ +
n =1
−1
n
"
2n
2n!
y
h
2n
d
2n
Gx/
dx/
2n
"=
h
This form clarifies what is meant by the statement that the more G is differentiated, the
smaller the terms become, and also allows better assessment of the order of accuracy
of the results.
As approaches unity, equation (4.7.10) can be integrated in a simpler form. This
value of # gives a wave whose wavelength approaches infinity. It is called the solitary
wave, with L →h
trough
=h
. The result is
1.6
5
30
40
50
70
90
k
1.2
0.8
0.4
0.0
20 40
φ
E(k,
φ
)
60 800
Figure 4.7.1 Elliptic function Ek
136 Surface and Interfacial Waves
5
k
85
90
80
5
50
60
70
4
3
2
1
0
φ
F(k,
φ
)
0 20406080
Figure 4.7.2 Elliptic function Fk
2
=
3 −h
2
h
crest
−
h
crest
h
2
, which can be integrated to give
=h
+
h
crest
−h
cosh
2
05$x
with $ =
3h
crest
−h
h
2
h
crest
(4.7.13)
The speed necessary to keep this wave stationary can be found in this case by realizing
that far upstream the constant C in equation (4.6.13) is C =c
2
/2+gh
. Putting this in
the expression for L in equation (4.6.18) gives c =
gh
. Conversely, this would be
the speed at which the wave travels in otherwise still water.
Wehausen and Laitone (1960, §31) show that there is a theoretical limit to the
height of finite amplitude waves, given by
h
crest
−h
trough
h
max
=
8
2
9
2
+2
(4.7.14)
At this amplitude theory shows that there is a reversal in the vertical velocity near the
crest. For the solitary wave this has a value of 8/11 = 07273. Experiments with these
waves show that as the wave amplitude approaches this limit, the wave starts to break.
4.8 Ray Theory of Gravity Waves for Nonuniform Depths
When the depth of the flow is variable, particularly in shallow regions where depth is
comparable to wavelength, observations of waves from the shoreline show waves both
steepening and changing direction. To understand this phenomena, the approach must
be altered a bit from the previous.

4.8 Ray Theory of Gravity Waves for Nonuniform Depths 137
Since a three-dimensional problem is now being considered, choose z as being the
direction perpendicular to the free surface. The waves will be considered small so that
the linearized theory can be used. The governing equations are then
2
=0in0≤z ≤−hx y (4.8.1)
t
+g = 0onz =0 (4.8.2)
t
=
z
on z =0 (4.8.3)
z
=v
z
=−
x
h
x
+
y
h
y
on z =−hx y (4.8.4)
Since equation (4.8.4) involves products of function of x and y, methods such as
separation of variables cannot be used for general functions h(x,y).
To simplify the equations, certain assumptions must be made concerning the relative
values of the various quantities. The easiest way to do this is to deal with dimensionless
quantities. L will be taken to be an appropriate length, possibly a wavelength, measure
in the x-y plane, and changes in the z direction will be taken to occur at a faster rate
than in the x-y directions. Thus, "L will be the appropriate scale in the z direction. Our
dimensionless coordinates will then be X = x/L Y = y/L Z = z/"L, and H = "h/L.
The appropriate time dimensionalization is T =t
√
"g/L.
As a result of this,
x
=
1
L
X
y
=
1
L
Y
z
=
1
"L
Z
and
t
=
"g
L
T
Thus, our equations become
2
2
+
1
"
2
2
Z
2
=0in0≤ Z ≤−Hx y (4.8.5)
where
2
=i
X
+ j
Y
2
2
=
2
X
2
+
2
Y
2
Also,
"g
L
T
+g = 0
"g
L
T
=
1
"L
Z
on Z =0 (4.8.6)
1
"
Z
=−"
X
H
X
+
Y
H
Y
on Z =−H (4.8.7)
If these are rearranged and is solved for, the result is
"
2
2
2
+
2
Z
2
=0in0≤ Z ≤−Hx y (4.8.8)
=−
"
gL
T
T
=
1
"
3
gL
Z
on Z =0 (4.8.9)
138 Surface and Interfacial Waves
The displacement can be eliminated from consideration by differentiating the first
result in equation (4.8.9) and using it in the second. Thus,
Z
=−"
2
X
H
X
+
Y
H
Y
on Z =−H (4.8.10)
"
2
2
T
2
+
Z
=0onZ =0 (4.8.11)
To proceed with a solution, recall that in the constant-depth case there were solutions
like e
ikx−%t
to represent traveling waves. Here, in correspondence with this, write
XYZT =fX Y Ze
isXYT /"
. Substituting this into our equations yields
"
2
2
2
f +i"2
2
s ·
2
f +f
2
2
s +
2
f
Z
2
−
2
s
2
f
=0in0≤Z ≤−Hxy
f
Z
−
s
T
2
f
+i"
2
s
T
2
f =0onZ =0
f
Z
+i"f
2
s ·
2
H +"
2
2
f ·
2
H =0onZ=−H
As yet neither L nor " have been defined. In the constant depth case, it was seen
that the quantity kx −t corresponds to our sX Y T/", where k is the wave number
and the circular frequency. In analogy with this, it is customary to choose the scaling
so that s/T =1, which assumes the circular frequency
√
g/"L is independent of time,
and to write k =
2
s
as a wave number that depends on X and Y . This equation for k
is called the eikonal equation in geometric optics. (Eikonal is the Greek word for “ray.”
It sounds much more impressive than the short word ray.) The surfaces s = constant
are wave fronts, or lines of constant phase, and
2
s is a vector normal to the wave front
and represents a ray.
If everything has been scaled properly, the terms not multiplied by " should be
handled first. From them it is found as the lowest approximation to f that
f
0
=A
0
x y cosh kZ +H with k tanh kh =1 (4.8.12)
Checking back with the constant depth case, the results are the same, but now the wave
number k is a function of the horizontal coordinates.
The amplitude solution can be continued by writing
f =f
0
+
n =1
"
n
cosh kZ +HA
n
XYZ
and substituting into the equations and collecting terms on powers of &. The process is
tedious but straightforward. The approach is discussed in Meyer (1979).
Of main interest, however, is how a wave front moves. To carry out a solution
numerically, one would start with a given wave front (i.e., a given value of s). At any
given depth, H is known, so k can be found. The eikonal equation plus the known
directionality of
2
s at any point (perpendicular to the wave front) is then integrated
to find the ray direction and establish a new wave front. The process repeats until a
boundary is encountered.
Note that it is possible that rays can cross one another, just as light rays cross when
focusing a beam of light. The intersection of two rays is called a caustic. Where they
intersect, our theory predicts infinite amplitude of the wave. In fact, our theory breaks
Problems—Chapter 4 139
down there, just as it does at the envelopes of the rays. The same happens in geometric
optics theory. In both cases a different scaling is needed.
To summarize, in dimensional terms the various quantities in terms of dimensional
units are given by
dimensional wave number →k
D
=
1
"
2
s
=
k
"L
,
dimensional circular frequency →
D
=
1
"
s
T
=
g
"L
,
dimensional wave speed →c
D
=
D
k
D
=
√
"gL
k
,
dimensional wave length →
D
=
2
k
D
=
2"L
k
.
The monograph by Mader (1988) presents more details as well as numerical pro-
grams for calculating the progress of such waves.
Problems—Chapter 4
4.1 For a monochromatic (a single wavelength) traveling wave on a deep layer
of fluid, the potential and the elevation are given by xt =−ace
ky
coskx −ct,
xt =a sin kx −ct. The kinetic and potential energies contained in one wavelength
are
KE =
1
2
0
−
0
x
2
+
y
2
dx −ctdy and PE =
1
2
g
0
2
dx −ct
Show that the two energies are equal. This is called the principle of equi-partition of
energy.
4.2 Find the wavelengths to be expected for standing waves on the free surface of
a rectangular tank a by b, with depth d.
4.3 Find the wavelengths to be expected for standing waves on the free surface of
a cylindrical tank of radius a and depth d.
4.4 Two fluids of different densities are separated by an interface at y = 0. The
fluids can each be considered to have infinite extent. Find the speed at which interfacial
waves travel, including the effects of surface tension. The linearized surface tension
condition can be taken as p =
2
x
2
.
4.5 Find the possible interfacial waves in a canal, where the bottom layer of depth
a has a higher density than the top layer of thickness b. The top layer is open to
the atmosphere. Neglect surface tension. (Ships moving in fjords where the top layer
is brackish and the lower layer is salty can notice increased ship drag due to waves
generated at the interface of the two fluids.)

Chapter 5
Exact Solutions of the Navier-Stokes
Equations
5.1 Solutions to the Steady-State Navier-
Stokes Equations When Convective
Acceleration Is Absent 140
5.1.1 Two-Dimensional Flow
Between Parallel Plates 141
5.1.2 Poiseuille Flow in a
Rectangular Conduit 142
5.1.3 Poiseuille Flow in a Round
Conduit or Annulus 144
5.1.4 Poiseuille Flow in Conduits
of Arbitrarily Shaped Cross-
Section 145
5.1.5 Couette Flow Between
Concentric Circular
Cylinders 147
5.2 Unsteady Flows When Convective
Acceleration Is Absent 147
5.2.1 Impulsive Motion of a Plate—
Stokes’s First Problem 147
5.2.2 Oscillation of a Plate—
Stokes’s Second Problem 149
5.3 Other Unsteady Flows When
Convective Acceleration Is Absent 152
5.3.1 Impulsive Plane Poiseuille
and Couette Flows 152
5.3.2 Impulsive Circular Couette
Flow 153
5.4 Steady Flows When Convective
Acceleration Is Present 154
5.4.1 Plane Stagnation Line
Flow 155
5.4.2 Three-Dimensional Axisymme-
tric Stagnation Point Flow 158
5.4.3 Flow into Convergent or
Divergent Channels 158
5.4.4 Flow in a Spiral Channel 162
5.4.5 Flow Due to a Round Laminar
Jet 163
5.4.6 Flow Due to a Rotating
Disk 165
Problems—Chapter 5 168
5.1 Solutions to the Steady-State Navier-Stokes Equations
When Convective Acceleration Is Absent
Because of the mathematical nonlinearities of the convective acceleration terms in the
Navier-Stokes equations when viscosity is included, and also because the order of the
Navier-Stokes equations is higher than the order of the Euler equations, finding solutions
is generally difficult, and the methods and techniques used in the study of inviscid
flows are generally not applicable. In this and the following chapters, a number of cases
140
5.1 Solutions to the Steady-State Navier-Stokes Equations When Convective Acceleration Is Absent 141
where exact and approximate solutions of the Navier-Stokes equations can be found are
discussed.
In particular, for flows where the velocity gradients are perpendicular to the veloc-
ity, the convective acceleration terms vanish. The results are then independent of the
Reynolds number. Several such cases will be considered.
5.1.1 Two-Dimensional Flow Between Parallel Plates
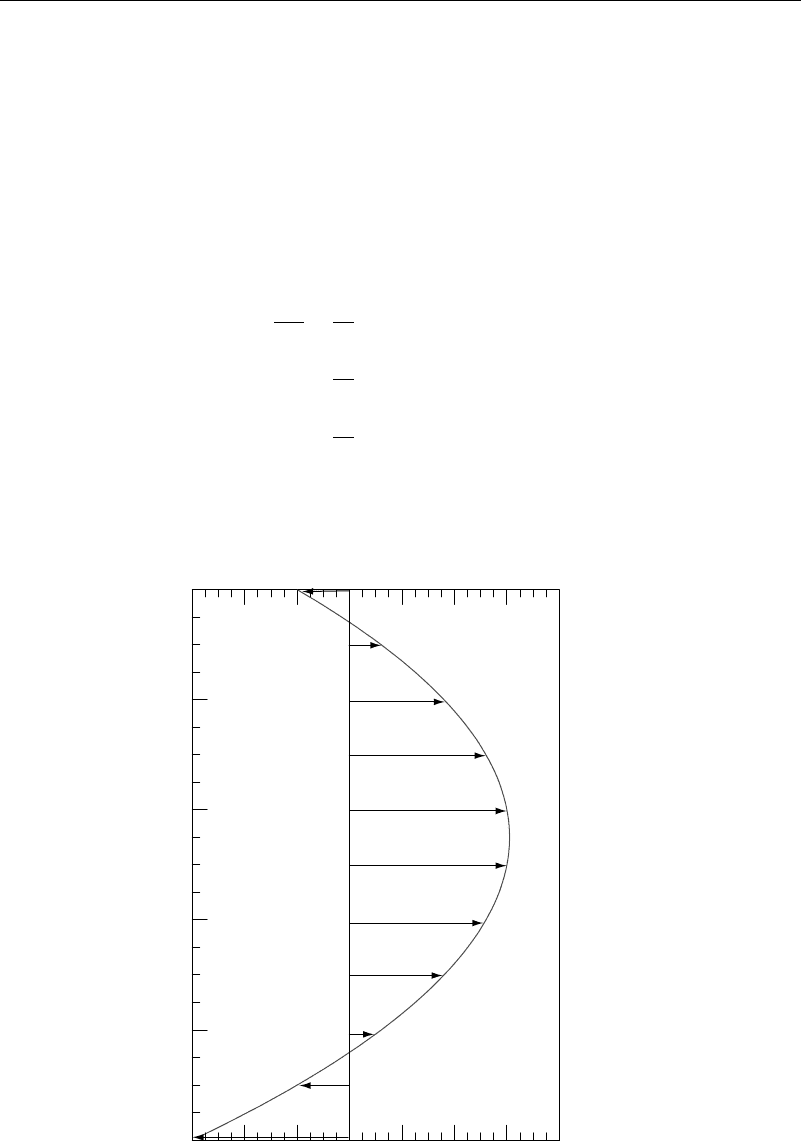
Consider flow between parallel plates as shown in Figure 5.1.1. Write the velocity in
the form v = uy 0 0, which automatically satisfies the continuity equation. With
gravity acting in the plane of the figure, the Navier-Stokes equations then become
d
2
u
dy
2
=
p
x
−g cos
0 =
p
y
−g sin (5.1.1)
0 =
p
y
where is the angle between the x-axis and the direction of gravity. Since the viscous
terms are functions of at most y, and since from the second and third equation p must
0.40.30.20.10.0–0.1–0.2–0.3
0.2b
0.4b
0.6b
0.8b
u
(y )
y
b
Figure 5.1.1 Plane Poiseuille-Couette flow
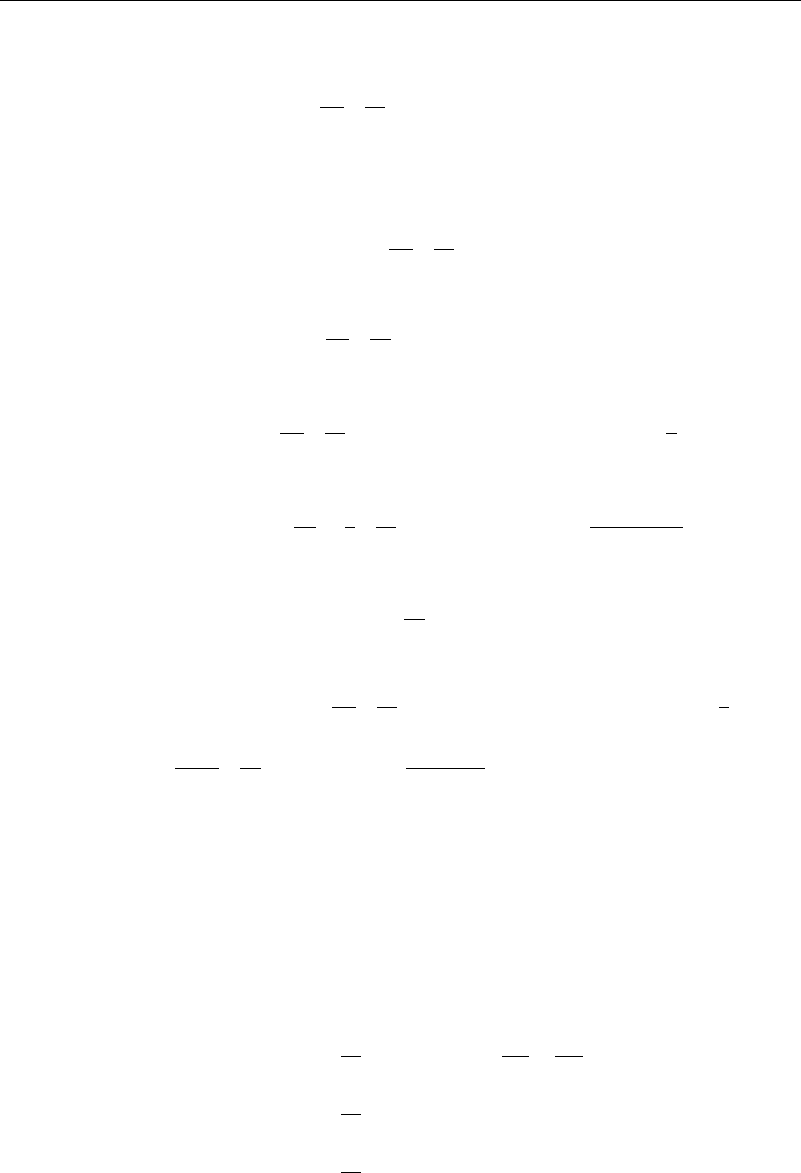
142 Exact Solutions of the Navier-Stokes Equations
be linear in y and independent of z p/x must be a constant. Thus, integration of
equation (5.1.1) gives
u =
1
2
p
x
−g cos
y
2
+c
1
y +c
2
where c
1
and c
2
are constants of integration.
If there is an upper plate at y = b moving with velocity U
b
, and a lower plate at y = 0
moving with velocity U
0
, then applying these conditions to our expression for u yields
U
0
=
c
2
2
p
x
−g cos
and
U
b
=
1
2
p
x
−g cos
b
2
+c
1
b +c
2
Solving for c
1
and c
2
gives
uy =
1
2
p
x
−g cos
y
2
−by +U
0
+U
b
−U
0
y
b
(5.1.2)
with a shear stress given by
xy
y =
du
dy
=
1
2
p
x
−g cos
2y −b +
U
b
−U
0
b
(5.1.3)
a pressure by
px y =
p
x
x +gy sin +p
0
(5.1.4)
and a volumetric discharge per unit width of
Q =a
b
0
udy=a
b
0
1
2
p
x
−g cos
y
2
−by +U
0
+U
b
−U
0
y
b
dy
=
−ab
3
12
p
x
−g cos
+ab
U
b
−U
0
2
(5.1.5)
The terms in the velocity that are associated with the pressure gradient and body forces
are called the Poiseuille flow terms. The terms due to the motion of the boundaries are
called the Couette flow terms.
5.1.2 Poiseuille Flow in a Rectangular Conduit
For flows in a rectangular conduit, the analysis is similar to that in the previous section
with of course one more space dimension, since the velocity depends on both y and z.
Letting v = uy z 0 0, the Navier-Stokes equations for this flow are
0 =−
p
x
+g cos +
2
u
y
2
+
2
u
z
2
0 =−
p
y
+g sin (5.1.6)
0 =−
p
y
5.1 Solutions to the Steady-State Navier-Stokes Equations When Convective Acceleration Is Absent 143
0.6
z
/b
y
/b
0.4
0.2
0.0
–0.2
–0.4
–0.6
0.0 0.2 0.4 0.6 0.8 1.0
Figure 5.1.2 Rectangular conduit—stream surfaces
with u = 0 on the (stationary) walls at 0 ≤ y ≤ b −05a ≤ z ≤ 05a as shown in
Figure 5.1.2.
Separation of variables suggests taking
u
s
=
1
2
p
x
−g cos
y
2
−by +YyZz
The terms quadratic in y are needed to make the equation homogeneous so that the
method of separation of variables works. Inserting this into equation (5.1.6) gives
0 =
d
2
Y
dy
2
Z +Y
d
2
Z
dz
2
, which after dividing by YZ becomes
1
Y
d
2
Y
dy
2
=−
1
Z
d
2
Z
dz
2
=a constant—say, −k
2
Solving these equations leads to Y being made up of sines and cosines of ky and Z
being hyperbolic sines and hyperbolic cosines of kx. Applying the no-slip boundary
conditions and symmetry in z eliminates the cosine and sinh functions. To meet the
remaining condition, it is necessary that k =
n
b
, where n is any positive integer. After
summing these in a Fourier series, the result is
u
x
=
1
2
p
x
−g cos
y
2
−by +
n=1
A
n
sin
ny
b
cosh
nz
b
(5.1.7)
with shear stress components
xy
=
u
x
y
=
1
2
p
x
−g cos
2y −b +
n=1
A
n
n
b
cos
ny
b
cosh
nz
b
xz
=
u
x
z
=
1
2
p
x
−g cos
n=1
A
n
n
b
sin
ny
b
sinh
nz
b
(5.1.8)
