Graebel W.P. Advanced Fluid Mechanics
Подождите немного. Документ загружается.


114 Irrotational Two-Dimensional Flows
Laurent series:Iffz is analytic on and between two concentric circles C and C
with center at z
0
is a point inside C, then fz can be expanded in positive and negative
powers of z −z
0
. It is convergent everywhere inside the ring-shaped region between C
and C
.
fz =
n=−N
a
n
z −z
0
n
(3.11.11)
Here, a
n
=
1
2i
(
fzdz
z−z
0
n+1
.
If N =, the function f is said to have an essential singularity at z
0
.IfN is a
positive nonzero number, f is said to have a singularity called a pole of order N at z
0
.
An example of an essential singularity is e
1/z
. Examples of poles of order one and two
are 1/z and 1/z
2
, respectively. Essential singularities are seldom encountered in flow
problems, while poles of orders one to four are frequently encountered in computing
forces and moments due to sources, sinks, vortices, and doublets.
You have no doubt already encountered the Taylor/Laurent series for real functions
in calculus classes. You may have wondered at that time why the expansion of 1/1−x
about the origin failed at both x =+1 and x =−1. The circle domains required by these
theorems affords an explanation of that question.
Example 3.11.1 Find the force exerted on a circular cylinder, center at the origin, and
with a radius a, in a uniform stream with circulation
Solution. From our earlier work, the complex potential is
w = U
z +
a
2
z
+
i
2
ln z
Thus,
dw
dz
2
=
U
1−
a
2
z
2
+
i
2z
2
=U
2
1−2
a
2
z
2
+
a
4
z
4
+
iU
z
1−
a
2
z
2
−
2z
2
When this is inserted into equations (3.11.8) and (3.11.9), Cauchy’s theorems tell us
that the only contribution is from the first order pole. Thus,
X = 0Y=U M =0
Problems—Chapter 3
3.1 a. Find the equation that the stream function must satisfy in order to represent
an irrotational flow in two dimensions. Use cylindrical polar coordinates.
b. Use separation of variables in the form r = RrT, and find the
equations that R and T must satisfy.
3.2 Show that for steady two-dimensional incompressible flow the acceleration can
be written as
dw
dz
∗
d
2
w
dz
2
∗
.

Problems—Chapter 3 115
3.3 It is sometimes convenient to regard a uniform flow as a source at minus
infinity and a sink at plus infinity, To demonstrate this, consider the potential for a
source of strength m at −a 0 and a sink of equal strength at a 0. Fix z, and expand
the complex potential in a Taylor series of z/a. Show that as a and m each go to infinity
such that their ratio remains constant, the result is a uniform stream of speed U =m/a.
3.4 Show that, if w
1
z represents the complex potential of a two-dimensional
irrotational flow and has no singularities in
z
<a, then wz = w
1
z +w
1
∗
a
2
/z
represents the same flow with a circle of radius a introduced at the origin. The
star represents that the complex conjugate of w
1
z is to be taken. This is known
as the circle theorem. It is a two-dimensional counterpart of the Weiss sphere
theorem.
3.5 Use the circle theorem to find the complex potential for a circular cylinder of
radius a in a flow field produced by a counterclockwise vortex of strength located
at the point z = b, where b>a. Also find the location of the stagnation points on the
circle.
3.6 a. Write the complex potential for a uniform stream, a source of strength 2m
at −a 0, and sinks of strength m at (0, 0) and (a, 0).
b. Find the equation of the closed streamline.
c. What is the length of the closed body when m/2aU =2/3a=2?
3.7 A line vortex with circulation 10 is placed in a corner at (2, 3). There are walls
at x = 0 and at y =0.
a. Write the complex potential for the vortex and two corners.
b. Find the induced velocity at the vortex.
3.8 Find the complex velocity potential for a line vortex at the origin and between
two parallel walls at x = 0y±a. Hint: Multiple mirrors are frequently encountered in
clothing stores, generating multiple reflections.
3.9 Show that the flow past a flat plate on the real z-axis is given by wz =
Ua cosh −i+
i
2
, where z =a cosh and U represents a uniform stream. The angle
is the angle between the plate and the uniform stream. The plate is at 0 ≤Imag
≤1
in the plane.
3.10 Show that the flow of fluid inside a rotating elliptical cylinder with semimajor
axes a and b is given by wz =iAz
2
. Find A in terms of the geometry and angular rate
of rotating. Hint: The boundary condition is =
1
2
x
2
+y
2
+constant.
3.11 Show that the flow of fluid outside a rotating elliptical cylinder with semi-
major axes a and b is given by wz = iAe
−2
, where z = c cosh . Find A in terms
of the geometry and angular rate of rotating. Hint: The boundary condition is =
1
2
x
2
+y
2
+constant.
3.12 a. Write the complex potential for a line vortex of circulation located at
z =ih and a line vortex of circulation − located at z =−ih. Show that the
x-axis is a streamline and so can be considered an infinite flat plate.
b. Calculate the pressure on the surface of the plate from the Bernoulli equation,
letting the pressure at infinity be zero. Integrate this pressure over the entire
length of the plate in order to find the force acting on the plate due to the
vortex.

116 Irrotational Two-Dimensional Flows
c. If a pair of sources, each of strength m, had been used, what would the
force be?
3.13 Using the method of images, find the complex potential for a vortex located
along the centerline of a channel of width a. The vortex is at point (b, 0), and the
channel is in the region x>0 −a/2 ≤y ≤a/2.
3.14 Show that the flow about a circular arc can be found using the Joukowski
transformation with an intermediate translation of axes that puts the origin on the vertical
axes. This means that both the leading and trailing edges lie on the surface of the arc.
3.15 Show that the transformation that maps the interior of the sector 0 ≤ ≤/n, n
an integer, in the z plane onto the upper half of the plane is =z
n
. Then if w =A A
real, represents a uniform stream in the plane, find the corresponding flow in the
z plane.
3.16 The infinite strip shown can be regarded as a two-sided polygon and hence the
Schwarz-Christoffel transformation can be used to transform it into the upper-half plane.
Find the transformation that puts A and D at infinity and B and C at the origin in the upper-
half plane. Take the width of the strip to be h.
C
D
BA
–∞∞
–∞∞
z plane
B, C DA
ζ plane
Figure P3.16 Problem 3.16—Infinitely long strip
3.17 The semi-infinite strip shown can be regarded as a three-sided polygon, hence
the Schwarz-Christoffel transformation can be used to transform it into the upper-half
plane. Find the transformation that puts A and D at infinity and B and C at plus and
minus one in the upper-half plane. Take the width of the strip to be h.
AB DC
–1 1
ζ plane
–∞∞
D
z plane
B
C
A
∞
Figure P3.17 Problem 3.17—Semi-infinitely long strip
Problems—Chapter 3 117
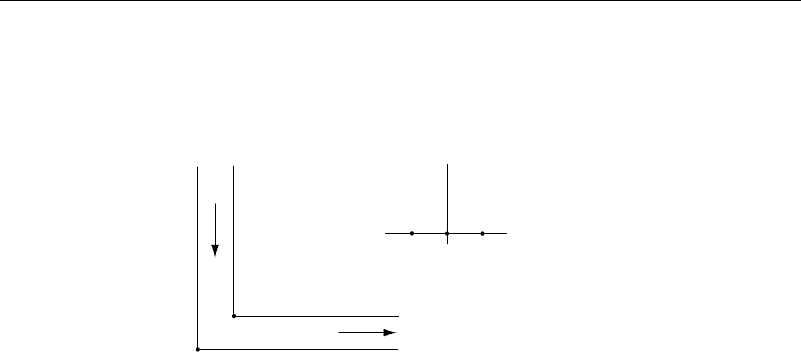
3.18 The Schwarz-Christoffel transformation can be used to transform the right-
angle 90-degree bend shown into the upper-half plane. The bend can be thought of
as a four-sided polygon. Find the transformation that places the corner A at 1, B at the
origin, C at −1, and D at infinity in the plane.
B
B
–∞
z plane
U
D
ζ plane
C
–1
1
A
A
C
D
∞
Figure P3.18 Problem 3.18—Elbow

Chapter 4
Surface and Interfacial Waves
4.1 Linearized Free Surface Wave
Theory 118
4.1.1 Infinitely Long Channel 118
4.1.2 Waves in a Container of
Finite Size 122
4.2 Group Velocity 123
4.3 Waves at the Interface of Two
Dissimilar Fluids 125
4.4 Waves in an Accelerating
Container 127
4.5 Stability of a Round Jet 128
4.6 Local Surface Disturbance on a Large
Body of Fluid—Kelvin’s Ship
Wave 130
4.7 Shallow-Depth Free Surface Waves—
Cnoidal and Solitary Waves 132
4.8 Ray Theory of Gravity Waves for
Nonuniform Depths 136
Problems—Chapter 4 139
Many different mechanisms for wave propagation in fluids exist. Compressibility of both
liquids and gases allows for compression waves such as sound waves and shock waves.
These generally have quite large velocities of propagation. Normally, they cannot be
seen by the human eye without suitable instrumentation or lighting. Waves on surfaces
and interfaces, on the other hand, are generally slower and can be observed easily.
Gravity, inertial forces, surface tension, and viscosity are also important mechanisms in
generating waves.
Much of the work presented in this chapter was originated by three English scien-
tists: Lord Kelvin (born William Thomson, 1824–1907), Lord Rayleigh (born William
Strutt, 1842–1919), and Sir Horace Lamb (1848–1934). The names in the literature for
the first two can be confusing, because, for example, both Kelvin and Thomson are
used, depending on whether the date of publication preceded or followed the bestowing
of honors. Much of the work is summarized in the books by Rayleigh (1945) and Lamb
(1932), and in the lengthy review in Wehausen and Laitone (1960).
4.1 Linearized Free Surface Wave Theory
4.1.1 Infinitely Long Channel
Consider the case of small amplitude waves in a two-dimensional channel of constant
depth h, an infinite length in the x direction, and having a uniform stream of velocity
118

4.1 Linearized Free Surface Wave Theory 119
U. It is convenient to choose a coordinate system with an origin on the undisturbed
free surface. When dealing with an unsteady flow problem with a free surface, it is
necessary to find the pressure by using the Bernoulli equation. Therefore, working with
the velocity potential, rather than the stream function, is indicated.
Write the total velocity potential in the form =Ux +
, where
represents the
velocity field due to the waves. The equations to be solved are then
2
=0 (4.1.1)
such that
y
=v
y
=0ony =−h (4.1.2)
Also, if the free surface is elevated an amount xt from the static position, then
p
=−
t
+
2
2
+g
+
1
R
1
+
1
R
2
=constant on y = (4.1.3)
and
D
Dt
=
y
=v
y
on y = (4.1.4)
(see Figure 4.1.1). Here, is the surface tension and R
1
and R
2
are the principal radii
of curvature. Since the pressure above the free surface is constant and can be taken as
gauge pressure, it can usually be set to zero.
Equation (4.1.4) states that the free surface moves up and down with a velocity
equal to the vertical component of the fluid velocity. If this problem were to be solved
with all nonlinearities included, it would be necessary to work instead with the vector
, which is the total vector displacement of a fluid particle on the free surface, and to
replace equation (4.1.4) by
D
Dt
=
D
Dt
=
1
2
2
−g
y
on the free surface D/Dt = v. Here, is the vertical component of .
Even though equation (4.1.1) is linear, the boundary conditions equations (4.1.3)
and (4.1.4), together with the fact that the free surface position is a priori unknown
make the problem highly nonlinear. Only in a few very special cases can a closed form
expression be found. Instead, consider the case of waves whose amplitude is small
h
x
y
Static position
η
Figure 4.1.1 Wave definitions—two dimensions

120 Surface and Interfacial Waves
compared to their wavelength, and replace the exact free surface conditions in equations
(4.1.3) and (4.1.4) by the linearized conditions
t
+U
x
+g =
2
x
2
on y =0 (4.1.5)
t
+U
x
=
y
on y =0 (4.1.6)
Here, the problem has been simplified still further by imposing equations (4.1.5) and
(4.1.6) at the static position y =0 rather than on the actual surface. The problem is now
amenable to analysis by the method of separation of variables.
Start by assuming that can be written as the superposition of terms like
xyt =Tt Xx Yy (4.1.7)
and insert this form into equation (4.2.1). The result is
TX
xx
Y +TXY
yy
=0
Divided by , this becomes
X
xx
/X +Y
yy
/Y = 0
Since the first term depends only on x and the second depends only on y, this relationship
can hold throughout the flow region only if each term is itself a constant. Thus,
Y
yy
/Y =−X
xx
/X = constant =k
2
say
The form of the constant k
2
has been selected by “looking ahead” at the solution. It
is expected that the disturbance will be oscillatory in the x direction and also that it
will die out away from the free surface. Making this decision now is not necessary,
but it does save a lot of cumbersome and confusing notation later on. Experience with
separation of variables problems, and a little foresight, can be very useful in avoiding a
morass of symbols.
The X solutions are then trigonometric functions of kx, and the Y solutions are
hyperbolic functions of ky. Taking equation (4.1.2) into account, using DeMoive’s
theorem that e
i
=cos +i sin , write
X = Ae
ikx
+Be
−ikx
(4.1.8)
Y = D cosh ky +h (4.1.9)
Since both D and T multiply the still unknown constants A and B in X, at this
point D and T can be combined with A and B, letting
=cosh ky +h
Ate
ikx
+Bte
−ikx
Guided by this form for the velocity potential, choose
=Fte
ikx
+Gte
−ikx
Substituting these expressions into equations (4.1.5) and (4.1.6), it is found that for
these boundary conditions to be satisfied for all x it is necessary that
A =
1
k sinh kh
dF
dt
+ikUF
B=
1
k sinh kh
dG
dt
−ikUG
(4.1.10)

4.1 Linearized Free Surface Wave Theory 121
and
F =−
cosh kh
g +k
2
dA
dt
+ikUA
and G =−
cosh kh
g +k
2
dB
dt
−ikUB
(4.1.11)
Combining these equations and letting
2
=k tanh kh
g +k
2
(4.1.12)
results in
A =−
1
2
d
2
A
dt
2
+2ik
dA
dt
−k
2
U
2
A
and B =−
1
2
d
2
B
dt
2
−2ik
dB
dt
−k
2
U
2
B
These have solutions like A = e
−ikUt
ke
it
+ke
−it
, B = e
ikUt
ke
it
+
ke
−it
.
Combining these results gives finally
=cosh ky +h
e
ikx−Ut
ke
it
+ke
−it
+e
−ikx−Ut
ke
it
+ke
−it
(4.1.13)
=i
sinh kh
e
ikx−Ut
ke
it
−ke
−it
+e
−ikx+Ut
ke
it
−ke
−it
(4.1.14)
These represent a wave traveling upstream with a velocity U ±/k and are called
traveling waves. The parameters k and are called the wavenumber and circular
frequency, respectively. The wavelength of the wave is given by = 2/k and the
wave speed relative to the uniform speed by
c =
k
=
1
k
g +k
2
tanh kh (4.1.15)
For depths large compared to the wavelength (the long wave case) tanh kh ≈ 1 and
c ≈
g +k
2
2
. For shallow depths, tanh kh ≈ kh and c =
k
=
hg +k
2
.If
surface tension effects are not important, the wave speed reduces to c ≈
√
gh and could
have been found by elementary momentum considerations.
The fact that the wave speed depends on the wave number means that the wave
is dispersive. That is, if a wave consists of two or more wave numbers, as the wave
propagates, each component moves at a different speed, so the wave disperses, or
changes shape, as it travels.
Since waves on a very large body of water are being considered, with x extending
to infinity in both directions, there are no boundary conditions left to determine k.
Thus, there can be a continuous spectrum of k. The linearity of the problem allows for
superposition of wave numbers, leading to a solution in the form of a Fourier integral.
This is conveniently written as
xyt =
−
xytkdk
xyt =
−
xytkdk (4.1.16)

122 Surface and Interfacial Waves
where is given by equation (4.1.12). Information on the initial shape and velocity of
the disturbance is necessary to determine , and , and to be able to carry out the
integrations.
Undersea earthquakes generate waves of very long wavelengths, giving rise to
waves called tsunamis, which can travel at very high speeds across the ocean. In deep
water these waves are of small amplitude, and ships encountering such waves at sea may
not experience much if any of a disturbance as the waves pass. However, as the waves
approach shallow water near the shore, the previous results for wave speed show that
they slow down and, by exchanging their kinetic energy for potential energy, steepen
drastically, frequently causing catastrophic damage and loss of life. This explanation
also can be used to understand wave amplification and breaking of waves on beaches.
Waves caused by high winds such as hurricanes can be of large amplitude near the
driving force but do not tend to steepen as much.
4.1.2 Waves in a Container of Finite Size
If there are walls at the ends of our channel, reflections will occur and the traveling
wave form of the solution is no longer convenient for describing the behavior of the
flow. Instead of the e
±ikx
in equation (4.1.8) a better selection is to use cos kx and sin
kx. If the channel is bounded at x =0 and at x =L, then /x = 0 at those locations.
This rules out the use of sin kx and requires that sin kL = 0. This gives k = n/L,
where n is any positive integer greater than zero. Our solution now becomes
=
n =0
A
n
t cos
nx
L
cosh ky +h (4.1.17)
The boundary conditions still to be satisfied are
t
+g =
2
x
2
on y =0 (4.1.18)
and
t
=
y
on y =0 (4.1.19)
The U term has been dropped because the boundaries do not allow a uniform stream.
Taking the displacement of the form =
n =0
F
n
t cos nx/L and applying
equations (4.1.18) and (4.1.19) results in
n =0
dA
n
dt
cos
nx
L
cosh kh =−
n =0
g +
n
2
2
L
2
F
n
cos
nx
L
n =0
dF
n
dt
cos
nx
L
=
n =0
kA
n
sinh kh cos
nx
L
Using the orthogonality properties of the cosines by multiplying each side of the above
by cosmx/L and then integrating over the channel length gives
dA
n
dt
cosh kh =−
g +
n
2
2
L
2
F
n
dF
n
dt
=kA
n
sinh kh
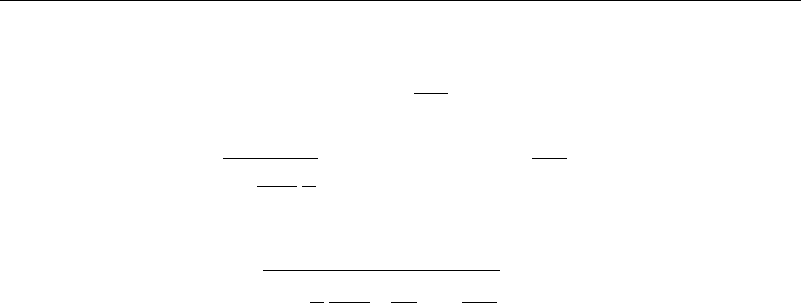
4.2 Group Velocity 123
Solving these for A
n
and F
n
results in
=
n =0
a
n
sin t +b
n
cost cos
nx
L
cosh ky +h (4.1.20)
=−
n =0
cosh kh
g +
n
2
2
L
2
a
n
cost −b
n
sin t cos
nx
L
(4.1.21)
with
n
=
g +
n
2
2
L
2
n
L
tanh
nh
L
(4.1.22)
The solutions in equations (4.1.21) and (4.1.22) are in the form of Fourier series, whose
coefficients can be found by imposing initial conditions on and /t. The solution
given by equations (4.1.20) and (4.1.21) is referred to as a standing wave.
It is important to understand how the physics and mathematics have interacted.
Laplace’s equation is said to be of elliptic type. This type of equation governs phenom-
ena such as steady-state heat transfer, deformation of membranes, and flow in porous
media. Normally, waves are not anticipated when dealing with such equations. The
free surface conditions have altered the physics of the situation, giving solutions that
in mathematics are more usual to equations of hyperbolic type—equations that permit
waves.
Wave behavior was clearly seen in the case where the channel extended to infinity
in the x direction. When the x extent was finite, this wave nature was concealed by the
form of the solution. Consider, for instance, a wave that starts out traveling to the right.
It will have a solution of the form e
imx −t
. When it encounters a wall, it is reflected
and becomes a left-traveling wave with the form e
−imx +t
. This wave is reflected
at the left wall, and the process repeats endlessly. The presence of the wall selects
waves—that is, it allows only certain wave numbers to be present. The form of the
solution in turn breaks down the exponential e
imx ±t
into sin mx cosmx sint, and
cost—thus disguising the traveling wave nature of the solution. The infinite domain
case with no walls present and solutions like e
imx ±t
results in traveling waves with the
general solution of the form fx −ct +gx +ct. In the finite domain case, because of
reflections from walls, solutions like sin mx sin t or cos mx cos t result in standing
waves after startup conditions have occurred.
4.2 Group Velocity
In the previous section it was stated that because the wave speed depended on the wave
number, the waves were dispersive. That means that if a wave shape is broken down into
Fourier components and more than one wave number is present, the wave shape would
change as the wave proceeds. If one observes an isolated group of waves traveling with
nearly the same wavelength, some of the waves are observed to proceed through the
group until it approaches the front of the group. At that point they appear to die out.
The process is then repeated by other waves.
