Готман Э.Г. Стереометрические задачи и методы их решения

Подождите немного. Документ загружается.

положим: a = x

, b = y

, c = z

. Тогда доказываемое неравенство приво-

дится к виду:

+ y

+ z

− 3xyz > 0.

Многочлен, стоящий в левой части неравенства, разложим на множи-

тели:

+ y

+ z

− 3xyz = (x + y)

+ z

− 3xy(x + y + z) =

= (x + y + z)(x

+ y

+ z

− xy − yz − zx).

Из приведённого выше неравенства следует, что

+ y

+ z

− xy − yz − zx > 0.

Учитывая, что x + y + z > 0, получаем:

+ y

+ z

− 3xyz > 0.

Равенство здесь имеет место тогда и только тогда, когда x = y = z, что

для исходного неравенства равносильно условию a = b = c.

Из неравенства

√

abc 6

a + b + c

следует, что если a + b + c = k, где k —

постоянное число, то abc 6





, причём равенство имеет место тогда

и только тогда, когда a = b = c.

Другими словами, произведение нескольких (в приведённом слу-

чае — трёх) положительных переменных сомножителей, сумма которых

постоянна, имеет наибольшее значение при равенстве сомножителей.

Точно так же, с умма нескольких положительных переменных сла-

гаемых, произведение которых постоянно, имеет наименьшее значение

при равенстве слагаемых.

Пользуясь этими следствиями, можно получить экономные решения

ряда геометрических задач на максимум и минимум.

Предварительно поле зно решить несколько примеров на нахождение

экстремальных значений функций э лем ентарными способами. Напри-

мер, следующие.

Найти наименьшие значения функций:

1) y = 4x +

, x > 0 (y = 4 при x =

);

2) y = x

− 4x + 3 (y = −1 при x = 2).

Найти наибольшие значения функций:

3) y = x

√

4 − x

, 0 < x < 2 (y = 2 при x =

√

2);

4) y = x

(a − 2x), 0 < x <

Представим функцию y в виде произведения: y = x ·x ·(a −2x). Так

как сумма сомножителей — постоянное число: x + x + (a − 2x) = a, то

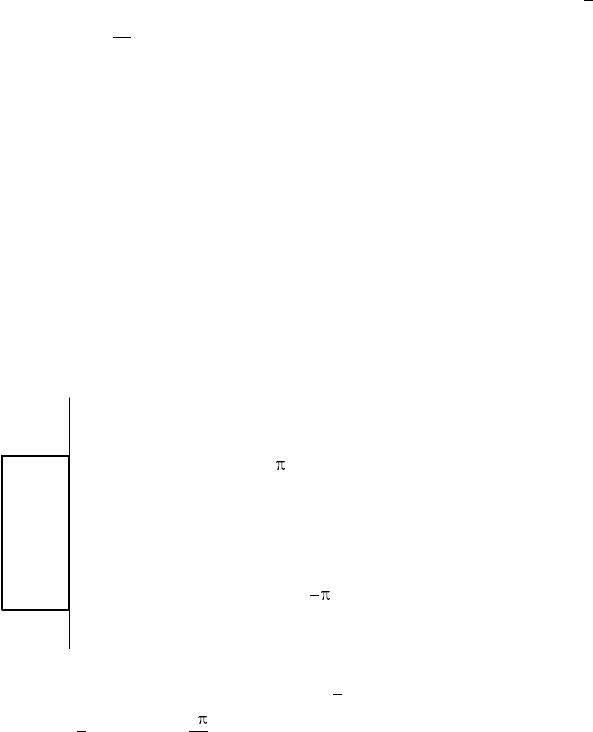
функция y принимает наибольшее значение при x = a −2x, т. е. x =

при этом y

max

Большинство стереометрических задач на отыскание наибольших

и наименьших значений решается аналитически. Чаще всего ис польз у-

ется соответствующая формула, выбирается независимая переменная,

которую обычно обозначают буквой x, получают функцию, выражаю-

щую величину, наибольшее или наименьшее значение которой требу-

ется найти, оп ред ел яют границы изменения аргумента x. Получен ная

функция иссл едуется элементарными методами или средствами мате-

матического анализа.

П р и м е р 1. Найти прямоугольник данного периметра 2p, который

вращением вокруг одной из своих сторон образует цилиндр наибольше-

го объёма.

Р е ш е н и е. Пусть прямоугольник ABCD вращается вокруг сторо-

ны CD (рис. 27). Согласно условию задачи AB + BC = p. Введём неза-

B C

p −x

Рис. 27

висимую переменную: BC = x. Тогда AB = p −x. Объём

V цилиндра, полученного при вращении прямоугольни-

ка, выразится функцией:

V = x

(p − x), 0 < x < p.

Наибольшее значение функции V можно найти без

использования производной. Представим выражение V

следующим образом:

V =

x · x(2p − 2x).

Так как сумма сомножителей, содержащих x, постоян-

на и равна 2p, то их произведение будет наибольшим

при x = 2p −2x, т. е. x =

p. Высота цилиндра при этом

будет равна

p и V

max

Независимую перемен ную обычно можно выбрать разными сп особа-

ми. Её желательно выбрать так, чтобы более коротким путём получить

выражение искомой функции и чтобы это выражение было по возмож-

ности более простым.

П р и м е р 2. В сферу радиуса R вписан конус. При какой высоте

конуса его объём будет наибольшим?

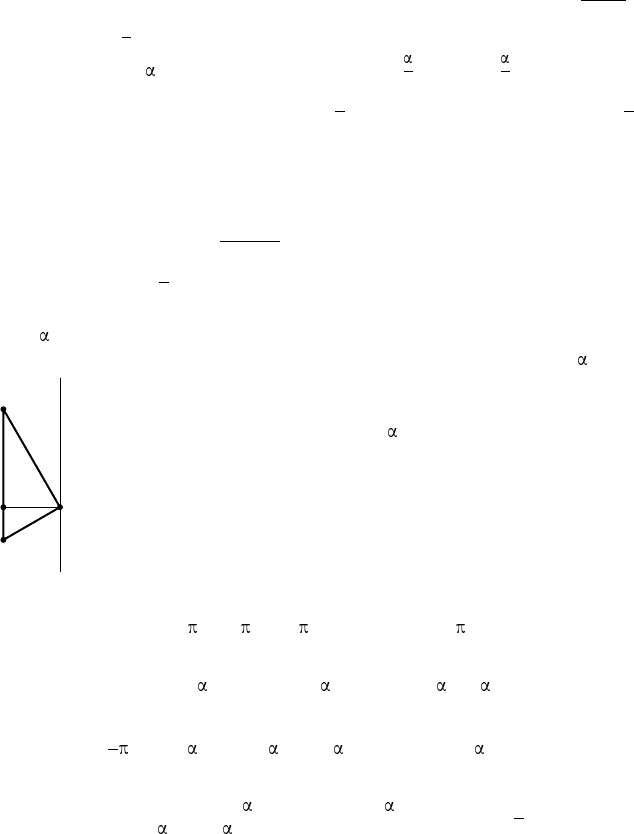
Р е ш е н и е 1. Обозначим через r и h радиус основания и высоту

конуса соответственно. Осевое сечен ие конуса — равнобедренный тре-

угольник ABN, вписанный в окружность, диаметр MN которой равен

DA B

Рис. 28

2R, ND — высота конуса, AD — радиус его

основания (рис. 28). Воспользуемся формулой

объёма конуса:

V =

За независимую переменную удобно при -

нять h. Так как ∠M AN = 90

◦

, то треугольник

MAN — прямоугольный и в силу известной

теоремы планиметрии сразу получаем:

= MD · DN, или r

= (2R − h) · h.

Таким образом, объём V конуса есть функция

переменной h:

V =

(2R − h)h

, 0 < h < 2R.

Наибольшее значение функции V можно почти устно найти без исполь-

зования производной. Рассмотрим произведение

(4R − 2h) · h · h.

Сумма положительных сомножителей постоянна, она равна 4R, значит,

произведение будет наибольшим при h = 4R − 2h, откуда h =

Итак, при h =

R объём конуса — наибольший и, как легко подсчи-

тать, V

max

Р е ш е н и е 2. Примем за независимую переменную величину угла

наклона образующей конуса к плоскости его основания, обозначим

∠DAN = x (см . рис. 28). Переменные h и r можно выразить чер ез R

и x из прямоугольных треугольников AM N и ADN. Получим:

AN = 2R sin x, h = AN sin x = 2R sin

x, AD = 2R sin x cos x.

Значит, V =

sin

x cos

x, 0

◦

< x < 90

◦

Потребовались более длинные вычисления, чем при решении задачи

первым способом. Покажем, что наибольшее значение функции V снова

можно найти без применения производной.

Функция V имеет наибольшее значение одновременно с функцией

y = 2 sin

x cos

x, или y = sin

x · sin

x · (2 − 2 sin

x),

т. е. при sin

x = 2 − 2 sin

x. Отсюда sin x =

. Остаётся найти соот-

ветствующее значение h. Подставив найденное значение sin x в формулу

h = 2R sin

x, пол учим h =

Заметим, что наибольшее или наим ен ьшее значение комбинации

тригонометрических функций иногда очень просто найти, если исполь-

зовать подходящие формулы тригонометрии. Приведём примеры.

Найти наибольшее значение функции:

1) y = sin x cos x, 0

◦

< x < 180

◦

Используя формулу синуса двойного аргумента, получаем: y =

sin 2x

Значит, y

max

при x = 45

◦

2) y = sin x sin( − x). О т в е т. y

max

= sin

при x =

3) y = sin x + cos x.

Используя формулу sin x +cos x =

√

2 sin(x + 45

◦

), получаем y

max

√

при x = 45

◦

4) y = a sin x + b cos x.

Воспользуемся тождеством:

(a sin x + b cos x)

+ (a cos x − b sin x)

= a

+ b

Откуда a sin x + b cos x 6

√

+ b

. Равенство имеет место тогда и только

тогда, когда tg x =

П р и м е р 3. Прямоугольный треугольник с гипотенузой c и острым

углом вращается вокруг оси, проведённой через вершину прямого угла

Рис. 29

параллельно гипотенузе. При каком значении угла пло-

щадь поверхности тела вращения будет наибольшей?

Р е ш е н и е. Пусть прямоугольный треугольник ABC

с гипотенузой AB = c и углом , вращается вокруг оси l,

параллельной AB (рис. 29). Поверхность те ла вращения

состоит из боковой поверхности цилиндра с образующей c

и боковых поверхностей двух конусов. Радиусы оснований

как цилиндра, так и конусов, равны высоте CD треуголь-

ника ABC.

Введём обозначения: CD = r, BC = l

, AC = l

. Пло-

щадь S поверхности вращения выражается формулой:

S = 2 cr + rl

+ rl

, или S = r (2c + l

+ l

Из прямоугольных треугольников ABC и ACD имеем:

= c sin , l

= c cos , r = c sin cos .

В итоге получаем:

s =

sin 2 (2 + sin + cos ), где 0

◦

< < 90

◦

Надо найти наибольшее значение функции S. Замечаем, что наиболь-

шее значение функции sin 2 равно 1 при = 45

◦

, а наибольшее зна-

чение функции sin + cos , как показано выше, равно

√

2, также при

= 45

◦

. Значит, и S имеет наибольшее значение при = 45

◦

, причём

max

(2 +

√

2).

Замечаем, что тот же результат можно было бы получить и геомет-

рическим путём, доказав, что высота CD, как и сумма катетов l

+ l

прямоугольного треугольника ABC, имеют наибольшее значение, когда

AC = BC, или = 45

◦

. Ясно, что если наибольшее значение функции S

находить с помощью производной, то вычисления будут очень громозд-

кими.

Далеко не все геометрические задачи на экстремум можно решить

с помощью элементарных приёмов. Поэтому важно овладеть общим

методом решения задач с пр им ене ни ем производной. Рассмотрим сле-

дующую задачу.

П р и м е р 4. Через диагональ правильной четырёхугольной приз-

мы проведена плоскость, пересекающая оба основания. Высота приз-

мы h, длина диагонали основания 2r. Найти наибольшее и наименьшее

значения площади сечения при 1) h = 2, r = 3; 2) h = 4, r = 9.

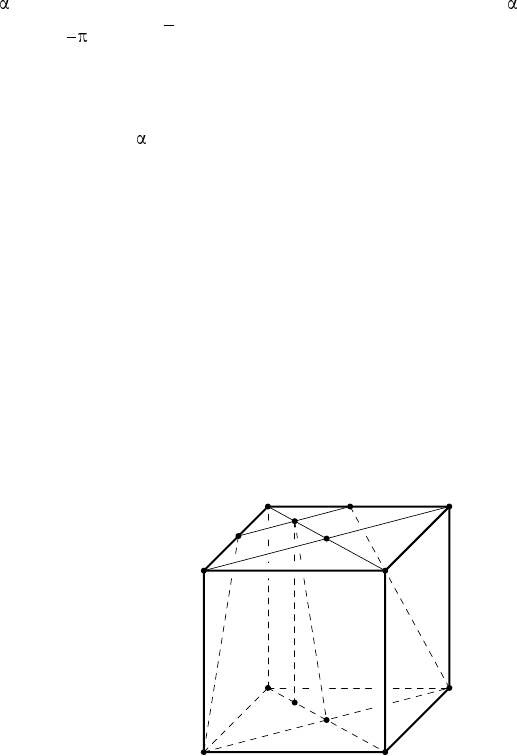
Р е ш е н и е. Пусть ABCDA

— правильная четырёхуголь-

ная приз ма, через диагональ AC которой проведена плоскость, пересе-

кающая отрезок B

в некоторой точке M (рис.

30). Центры квадратов

Рис. 30

ABCD и A

обозначим соответственно O и O

. Плоскость A

является плоскостью сим метр ии призмы. Поэтому достаточно рассмот-

реть случай, когда точка M принадлежит отрезку B

. Сечением

призмы является равнобочная трапеция ACEF , которая вырождается

в равнобедренный треугольник, если точка M совпадает с точкой B

и в прямоугольник, если M совпадает с точкой O

Призма симметрична относительно плоскости B

BD, MO — ось сим-

метрии сечения ACE, EM = MF = B

Проведём перпендикуляр MN к плоскости основания. Обозначив

M = x, имеем EF = 2x, NO = r − x,

MO =

(r − x)

+ h

Площадь сечения ACEF равна

S = (r + x)

(r − x)

+ h

, где 0 6 x 6 r.

Функция S положительна на отрезке [0; r] и имеет производную в каж-

дой его точке. Следовательно, задача сводится к нахождению наиболь-

шего и наименьшего значений функции y:

y = S

= (r + x)

− 2rx + r

+ h

)

на отрезке [0; r].

Найдём производную от функции y:

= 2(r + x)(2x

− 2rx + h

Так как r + x > 0, то y

= 0, если

− 2rx + h

= 0. (1)

1) При h = 2 и r = 3 уравнение (1) имеет вид

− 3x + 2 = 0,

откуда x

= 1 и x

= 2. Вычислив значения функции

= (3 + x)

(3 − x)

+ 4

в этих точках и на концах промежутка [0; 3], заполним таблицу 1.

Та б л и ц а 1

x 0 1 2 3

(x) 3

√

13 ≈ 10,8 8

√

2 ≈ 11,3 5

√

5 ≈ 11,1 12

Сравнивая найденные значения, видим, что функция S

принима-

ет наибольшее и наименьшее значения на концах промежутка [0; 3],

наибольшую площадь имеет диагональное сечение ACC

, а наимень-

шую — треугольник ACB

2) При h = 4 и r = 9 уравнение (1) имеет вид

− 9x + 8 = 0.

Отсюда x

= 1 и x

= 8. Вычислив значения функции

= (9 + x)

(9 − x)

+ 16

в этих точках и на концах промежутка [0; 9], составим таблицу 2.

Та б л и ц а 2

x 0 1 8 9

(x) 9

√

97 ≈ 88 40

√

5 ≈ 89 17

√

17 ≈ 70 72

По таблице видно, что функция S

принимает наибольшее значение

в точке x

= 1 и наименьшее в точке x

= 8.

Задача интересна тем, что при одних значения параметров функция

имеет экстремальные значения в критических точках, при других — на

концах промежутка. Ещё несколько задач такого рода вкл ючено в § 11.

§10. Применение элементарных методов

181. Среди п рямоугольных параллелепипедов с данной диагональю

найдите тот, который имеет наибольшую площадь полной поверхности.

182. а) Какую наибольшую площадь боковой поверхности может

иметь правильная четырёхугольная призма с данной диагональю d?

б) Из всех прямоугольных параллелепипедов с д анной диагональю

найдите тот, который имеет наибольшую площадь боковой поверхности.

183. Каковы должны быть размеры открытого бассейна данного объ-

ёма V , чтобы на облицовку его стен и дна пошло наименьшее количество

материала?

∗ ∗ ∗

184. а) В данный треугольник впишите прямоугольник наибольшей

площади так, чтобы одна сторона прямоугольника лежала на большей

стороне треугольника.

б) В данный конус впишите цилиндр с наибольшей площадью боко-

вой поверхности.

185. В данный конус впишите цилиндр наибольшего объёма.

186. В правильную четырёхугольную пирамиду впишите прямо-

угольный параллелепипед наибольшего объёма так, чтобы одна грань

параллелепипеда лежала в плоскости основания пирамид ы, а вершины

противоположной грани принадлежали боковым рёбрам.

∗ ∗ ∗

187. а) Из всех цилиндров, вписанных в данную сферу, найдите тот,

который имеет наибольшую площадь боковой поверхности.

б) В сферу вписан цилиндр с наибольшей площадью полной поверх-

ности. Чему равно отношение площади сферы к площади поверхности

цилиндра?

188. В сферу радиуса R вписана правильная n-угольная пирамида.

Какова должна быть высота пирамиды, чтобы её объём был наиболь-

шим?

∗ ∗ ∗

189. Около шара радиуса R описан конус. При какой высоте конуса

его объём будет наименьшим? Докажите, что

V > 2V

где V — объём конуса, V

— объём шара.

190. В правильную четырёхугольную пирамиду вписан куб так, что

четыре его вершины принадлежат боковым рёбрам пирамиды, а осталь-

ные четыре — плоскости её основания. Докажите, что

где V

— объём куба, V — объём пирамиды. При каком условии имеет

место равенство?

∗ ∗ ∗

191. Из квадратного листа жести со стороной a требуется сделать ко-

робку без крышки, вырезая по углам квадраты и загибая затем получа-

ющиеся выступы так, чтобы коробка получилась наибольшего объёма.

Каковы должны быть длины сторон вырезанных квадратов?

192. Боковое ребро правильной четырёхугольной пирамиды равно l.

При каком отношении высоты пирамиды к стороне основания объём

пирамиды будет наибольшим? Чему равен этот объём?

193. Образующая конуса равна l и составляет с основанием угол .

При каком значении объём конуса будет наибольшим? Чему равен

этот объём?

∗ ∗ ∗

194. Длины двух противоположных рё бер тетраэдра равны x, а все

остальные имеют длину, равную 1. Выразите объём тетраэдра как

функцию x. При каком значении x объём тетраэдра имеет наиболь-

шее значение?

195. Длина одного бокового ребра четырёхугольной пирамиды рав-

на x, все остальные рёбра имеют длин у, равную 1. Выразите объём

тетраэдра как функцию x. При каком з начении x объём пирамиды при-

нимает наибольшее значение?

∗ ∗ ∗

196. Куб, ребро которого равно a, пересекается плоскостью, прохо-

дящей через его диагональ. Какую наименьшую площадь может иметь

сечение и при каком угле наклона сечения к плоскости основания?

197. а) Тетраэдр ABCD пересечён плоскостью, параллельной его

рёбрам AD и BC. Найдите периметр сечения, если AD = BC = a.

б) Тетраэдр ABCD пересечён плоскостью так, что в сечении полу-

чился четырёхугольни к. Какое наименьшее значение может при ним ать

периметр сечения, если AD = BC = a, BD = AC = b, CD = AB = c?

198. Основанием пирамиды SABCD служит параллелограмм ABCD.

Через вершину A и середину K ребра SC проведена плоскость, пересе-

кающая рёбра SB и SD в точках M и N . Докажите, что

V 6 V

где V — объём пирамиды SABCD, а V

— объём пирамиды SAM KN.

При каком условии каждое неравенство обращается в равенство?

199. a) Докажите, что дл я любых положительных чисел a

, a

, . . . , a

и b

, b

, . . . , b

имеет место неравенство

+ b

+ . . . +

+ b

√

+ b

где a

+ a

+ . . . + a

= a, b

+ b

+ . . . + b

= b. При этом неравенство об-

ращается в равенство, если

= . . . =

б) Из всех треугольников ABC с общим основанием AB и данной

высотой CH най дите тот, который имеет наименьший периметр.

в) Из всех тетраэдров ABCD с общим основанием ABC и данной

высотой DH найдите тот, который им еет наименьшую площадь боковой

поверхности.

200. а) Докажите, что для любых действительных чисел a

, a

и b

, b

выполняется неравенство

+ a

+ b

причём равенство имеет место только, если

(неравенство

Коши—Буняковского).

б) Дан те траэдр ABCD, рёбра AD, BD, CD которого попарно пер-

пендикулярны, причём AD = a, BD = b , CD = c. Докажи те, что для

любой точки M, лежащей в грани ABC, сумма s расстояний от вер-

шин A, B и C до прямой DM удовлетворяет неравенству

s 6

2(a

+ b

+ c

При каком положении DM имеет место равенство? Рассмотрите част-

ный случай: a = b =

√

6, c = 2.

201. Из точки A, расп оложенной вне плоскости, проведены к ней пер-

пендикуляр AO и наклонные AB и AC. Известно, что BO = 1, CO = 2

√

и ∠BOC = 45

◦

. Найдите расстояние AO, при котором ∠BAC = 45

◦

. Ка-

кое наибольшее значение может принимать этот угол?

202. Около сферы описан конус. Какую наименьшую площадь боко-

вой поверхности может иметь конус, если площадь сферы равна Q?

203. Около сферы радиуса r описана правильная четырёхугольная

пирамида. При каком угле наклона боковой грани к плоскости основа-

ния площадь полной поверхности пирамиды будет наименьшей? Най-

дите значение этой площади.

§11. Применение производной

204. Бак цилиндрической формы должен вмещать V литров воды.

Каковы должны быть его размеры, чтобы площадь его поверхности без

крышки была наименьшей?

205. При каких размерах открытая цилиндрическая ванна с полу-

круглым поперечным сечением, поверхность которой равна S, имеет

наибольшую вместимость?

206. Консервная банка данного объёма V имеет форму цилиндра.

Каковы должны быть её размеры, чтобы на её изготовление пошло ми-

нимальное количество жести?

∗ ∗ ∗

207. В сферу радиуса R вписан цилиндр. При какой высоте цилиндра

объём его будет наибольшим?

208. Какой наибольший объём может име ть правильная треугольная

призма, вписанная в сферу радиуса R?

209. Объём правильной треугольной призмы равен V . Каковы долж-

ны быть высота и сторона основания, чтобы площадь полной поверхно-

сти призмы была наименьшей?

210. Около полушара радиуса r описан конус так, что центр основа-

ния конуса совпадает с центр ом шара. При какой высоте конус а объём

его будет наименьшим?