Готман Э.Г. Стереометрические задачи и методы их решения

Подождите немного. Документ загружается.

255. Докажите, что радиус сферы, вписанной в прямоугольный тет-

раэдр, может быть вычислен по формуле

r =

+ S

− S

a + b + c

где a, b, c — длины боковых рёбер , S — п лощад ь основания тетраэдра.

256. В плоскости основания ABC прямоугольного тетраэдра ABCD

взята точка L, одинаково удалённ ая от боковых граней. Докажите, что

l = DL =

abc

√

ab + bc + ca

(отрезок DL называется биссектрисой тетраэдра).

257. а) Докажите, что для всякого прямоугольного треугольника

с катетами a, b и гипотенузой c имеет место неравенство

a + b 6 c

√

б) Докажите, что площади граней прямоугольного тетраэдра удо-

влетворяют неравенству

+ S

6 S

√

где S — площадь основания.

При каком условии имеет место равенство?

258. Докажите, что площадь основания прямоугольного тетраэдра

и радиус описанной около него сферы связаны соотношением

√

3 6 2R

259. а) Докажите, что для всякого прямоугольного треугольника

имеют место неравенства:

h 6 (

√

2 + 1)r 6 l 6

√

S 6

a + b

√

c = R.

б) Докажите, что для всякого прямоугольного тетраэдра справедли-

вы неравенства:

h 6 (

√

3 + 1)r 6 l 6

√

abc

√

2(S

+ S

) 6

В каком случае каждое из этих неравенств обращается в равен-

ство?

260. В сферу радиуса R вписан прямоугольный тетраэдр, высота

которого h. Найдите боковые рёбра тетраэдра, если R = 3 и h = 2.

261. Какое наименьшее значение может иметь объём прямоугольного

тетраэдра, высота которого равна 2 м?

§14. Ортоцентрический тетраэдр

262. а) Докажите, что если высоты AA

и BB

тетраэдра ABCD

пересекаются, то его рёбра AB и CD перпендикулярны. Верна ли обрат-

ная теорема?

б) Докажите, что если две высоты тетраэдра пересекаются, то две

другие высоты также пересекаются.

263. а) Докажите, что если две пары противоположных рёбер тетра-

эдра взаимно перпендикулярны, то рёбра третьей пары также перп ен-

дикулярны.

б) Докажите, что все четыре высоты тетраэдра или их продолжения

пересекаются в одной точ ке тогда и только тогда, когда противополож-

ные рёбра тетраэдра перпендикулярны.

264. Докажите, что тетраэдр является ортоцентрическим тогда

и только тогда, когда выполнено одно из следующих условий:

а) основание одной из высот тетраэдра есть ортоцентр соответству-

ющей грани;

б) суммы квадратов противоположных рёбер равны;

в) бимедианы тетраэдра равны.

265. а) Высоты AA

и BB

тетраэдра ABCD пересекаются в точ-

ке H. Докажите, что точка H лежит на общем перпендикуляре прямых

AB и CD.

б) Докажите, что в ортоцентрическом тетраэдре общи е перпенди-

куляры трёх пар противоположных рёбер проходят через ортоцентр

тетраэдра.

266. Докажите, что в ортоцентрическом тетраэдре все плоски е углы

при одной вершине одновременно либо острые, либо прямые, либо ту-

пые, и одна из граней — остроугольный треугольник.

267. а) Докажите, что угол C треугольника ABC острый, прямой

или тупой , в зависимости от того, будет ли s < 0, s = 0 или s > 0, где

s = m

−

+ b

)

(a = BC, b = AC и m

— медиана треугольника, проведённая из верши-

ны C).

б) Докажите, что все плоские углы при вершине D ортоце нтри че-

ского тетраэдра ABCD острые, прямые и ли тупые, в зависимости от

того, будет ли s < 0, s = 0 или s > 0, где

s = m

−

+ b

+ c

)

(a = DA, b = DB, c = DC и m

— медиана тетраэдра, проведённая из

вершины D).

268. а) Докажите, что во всяком треугольнике ABC центр O опи-

санной окружности, центроид M и ортоцентр H принадлежат одной

прямой, причём OH = 3OM (прямая Эйлера).

б) окажите, что центр O описанн ой сферы, центроид M и орто-

центр H ортоцентрического тетраэдра ABCD принадлежат одной пря-

мой, причём точки O и H симметричны относи тельн о точки M (прямая

Эйлера ортоцентрического тетраэдра).

269. а) Докажите, что середины трёх сторон треугольника, осно-

вания трёх его высот и середины отрезков, соедин яющих ортоцентр

с вершинами треугольника, лежат на одной окружности (окружность

девяти точек).

б) Докажите, что в ортоцентрическом тетраэдре ц ен троиды четы-

рёх граней, основания четырёх высот тетраэдра и точки, которые делят

каждый из отрезков, соединяющих ортоцентр с вершинам и, в отноше-

нии 1 : 2, считая от ортоцентра, лежат на одной сфере (сфера 12 точек).

§15. Равногранный тетраэдр

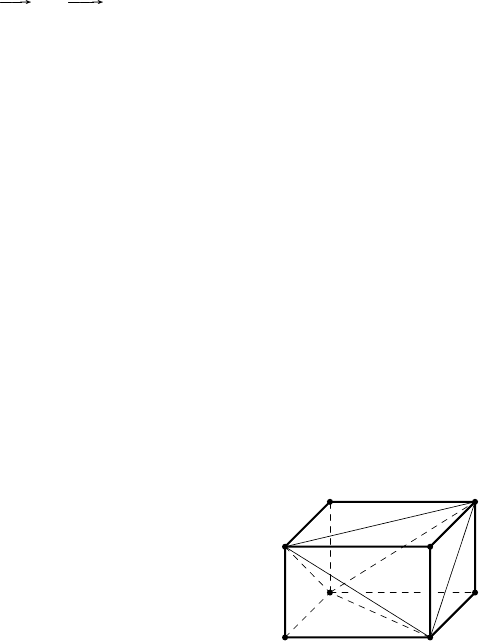
Тетраэдр называется равногранным, ес ли все его грани равны. Та-

кой тетраэдр можно построить. Проведём скрещивающиеся диагонали

Рис. 34

AB и CD двух противоположных граней

прямоугольного параллелепипеда. Легко до-

казать, что их концы являются вершина-

ми тетраэдра ABCD, противоположные рё-

бра которого равны, и, следовательно, рав-

ны и грани (рис. 34).

Обратно, если ABCD — равногранный

тетраэдр, то через каждое его ребро можно

провести плоскость, параллельную проти-

воположному ребру, и тем самым достроить

тетраэдр до прямоугольного параллелепи-

педа. Такое построение иногда помогает решить зад ачу о тетраэдре.

Рассмотрите сначала несколько простых задач.

270. а) Периметры четырёх граней тетраэдра равны. Докажите, что

противоположные рёбра тетраэдра равны.

б) Все грани тетраэдра — равные треугольники. Докажите, что про-

тивоположные рёбра равны.

271. Докажите, что грани равногранного тетраэдра — остроугольные

треугольники и сумма плоских углов при каждой вершине равна 180

◦

Верно ли обратное утверждение?

∗ ∗ ∗

272. Докажите, что тетраэдр равногранный тогда и только тогда,

когда выполняется одно из следующих условий:

а) бимедианы являются его осями симметрии;

б) медианы равны;

в) бимедианы попарно перпендикулярны;

г) суммы п лоск их углов при каких-либо трёх вершинах равны 180

◦

273. а) Гран и ABC и ABD тетраэдра ABCD равновелики. Докажи-

те, что общий перпендикуляр прямых AB и CD проходит через середи-

ну ребра CD.

б) Докажите, что если площади всех граней тетраэдра равны, то

тетраэдр равногранный.

274. Докажите, что тетраэдр равногранный тогда и только тогда,

когда его высоты равны.

∗ ∗ ∗

275. Около тетраэдра описан параллелепипед так, что скрещива-

ющиеся рёбра являются диагоналями противоположных граней па-

раллелепипеда. Докажите, что тетраэдр является равногранным тогда

и только тогда, когда описанный параллелепипед прямоугольный.

276. В тетраэдре ABCD проведены медианы DA

, DB

, DC

его

граней DBC, DAC, DAB. Докажите, что тетраэдр A

является

равногранным тогда и только тогда, когда трёхгранный угол D тетра-

эдра ABCD прямой (т. е. все плоские углы при вершине D тетраэдра

прямые).

∗ ∗ ∗

277. Докажите, что все грани тетраэдра равны тогда и только тогда,

когда выполняется одно из следующих условий:

а) центр сферы, описанной около тетраэдра, совпадает с его центро-

идом;

б) центр сферы, вписанной в тетраэдр, совпадает с его центроидом;

в) центр сферы, вписанной в тетраэдр, совпадает с центром описан-

ной около него сферы.

278. Докажите, что тетраэдр является равногранным тогда и только

тогда, когда его противоположные рёбра видны из центра описанной

сферы под равными углами.

279. Точка O — центр сферы, описанной около тетраэдра ABCD. До-

кажите, что равенство

OA + OB + OC + OD = 0

выполняется тогда и только тогда, когда тетраэдр ABCD равно-

гранный.

∗ ∗ ∗

280. Противоположные рёбра равногранного тетраэдра равны a, b, c.

Докажите, что

1) m =

R =

2(a

+ b

+ c

);

2) V =

2(a

+ b

− c

)(a

+ c

− b

)(b

+ c

− a

где R — радиус описанной сферы, m — медиана, V — объём тетра-

эдра.

281. Плоские углы при одной из вершин равногр анног о тетраэдра

равны , , . Докажите, что

4r = h = 4R

cos cos cos ;

V =

abc

cos cos cos .

282. Противоположные рёбра равногранного тетраэдра равны a, b, c.

Найдите расстояния между ними.

283. В тетраэдр е ABCD суммы трёх плоских углов при каждой

вершине равны 180

◦

. Найдите объём тетраэдра и расстояние между рё-

брами AB и CD, если BC = 4, CA = 5, AB = 6.

284. Найдите ради ус сферы, описанной около равногранного тетра-

эдра ABCD, если BC = AD = 6 см и расстояние между рёбрами BC

и AD равно 8 см.

285. Равногранный тетраэдр ABCD достроен до призмы ABCDB

(грань ABC — основание призмы). Докажите, что грань BCC

ромб.

Найдите расстояние от верши ны D до этой грани, если DA = a, DB = b

и DC = c.

Вычислите объём тетраэдра, пользуясь указанным построением.

286. Докажите, что сумма расстояний от любой точки, взятой вну-

три равногранного тетраэдра, до его граней есть величина постоянная.

Пользуясь этим свойством, докажите, что r =

h, где r — радиус впи-

санной сферы и h — высота равногранного тетраэдра.

287. Докажите, что радиус сферы, вписанной в равногранный тет-

раэдр, вдвое меньше радиуса сферы, касающейся одной грани и про-

должений трёх других граней.

∗ ∗ ∗

288. Докажите, что в равногранном тетраэдре противоположные

двугранные углы равны.

289. Величины двугранных углов произвольного тетраэдра равны

i = 1, 2, . . . , 6. Докажите, что

i=1

cos

6 2,

где равенство имеет место в том случае, когда тетраэдр равногранный.

290. Докажите, что для любого тетраэдра имеет место неравенство

+ b

+ c

+ a

+ b

+ c

которое обращается в равенство тогда и только тогда, когда тетраэдр

равногранный.

Г л а в а 7

Комбинации геометрических тел

В настоящей главе собраны задачи, требующие хороших простран-

ственных представлений. При решении их могут быть использованы как

геометрические, так и аналитические методы. Решение каждой задачи

следует начинать с тщательного выполнения чертежа. Иногда полез-

но сделать несколько чертежей и остановиться на том из них, который

является наиболее наглядным.

§16. Призмы и пирамиды

291. Дана четырёхугольная призма. Середины сторон её нижнего

основания и произвольная точка верхнего основания являются верши-

нами вписанной в призму четырёхугольной пирамиды. Найдите отно-

шение объёма пирамиды к объёму призмы.

292. Дан куб ABCDA

, ребро которого равно a. Найдите

объём тетраэдра, вершинами которого являются точка D

и середины

рёбер AB, BC и BB

куба.

293. Все плоские углы при вершине D тетраэдра ABCD прямые.

В тетраэдр вписан куб так, что одна его вершина совпадает с вер-

шиной D куба, а противоположная ей вершина лежит в грани ABC.

Вычислите длину ребра куба, если DA = a, DB = b и DC = c.

294. Высота правильной четырёхугольной пирамиды равна диагона-

ли её основания. В пирамиду вписан куб так, что четыре его вершины

лежат на апофемах пирамиды, а другие четыре — в плоскости основа-

ния. Объём пирамиды равен V . Найдите объём куба.

295. Даны правильная четырёхугольная пирамида и куб, вершинами

одной из граней которого являются середины рёбер основания пира-

миды. Каждое ребро противолежащей грани куба пересекает одно из

боковых рёбер пирамиды. Найдите отношение объёма куба к объёму

пирамиды.

296. Основанием четырёхугольной пирамиды NABCD служит квад-

рат. Боковые грани NAD и NCD пирамиды перпендикулярны плоско-

сти основания, а грань NAB образует с плоскостью осн ования угол .

В пирамиду вписан куб так, что четыре вершины куба лежат на боко-

вых рёбрах п ир амид ы, четыре други е — в плоскости основания. Найди-

те: а) отношение k объёма пирам ид ы к объёму куба; б) величину угла ,

при котором k =

; в) наим ен ьшее возможное значение k.

297. Высота правильной четырёхугольной пи рами ды вдвое больше

диагонали её основани я, объём пирамиды равен V . В пирамиду вписы-

ваются правильные четырёхугольные призмы так, что боковые рёбра

одной грани лежат в плоскости основания пирамиды и параллельны

диагоналям основания, а вершины противоположной грани лежат на

боковой поверхности пирамиды. Найдите наибольшее значение объёма

рассматриваемых призм.

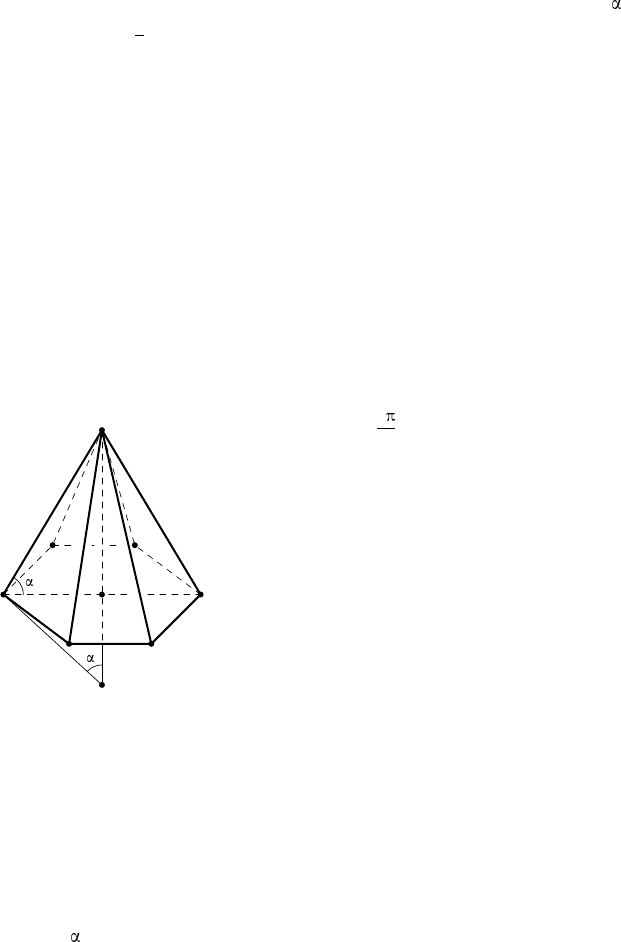
§17. Правильная пирамида и сфера

Как известно, около всякой правильной пирамиды можно описать

сферу и в неё можно вписать сферу. Пусть NH — высота правиль-

ной n-угольной пирамиды NA

. . . A

, точка H — центр её основания

Рис. 35

(рис. 35). При повороте пирамиды вокруг

оси N H на углы

(k = 1, 2, . . . , n −1) точки

оси, и только они, остаются на месте, вер-

шины же основания переходят в другие вер-

шины, а пирамида переходит в себя. В себя

переходят также сферы, описанн ая и впи-

санная. Значит, их центры — неподвижные

точки, лежащие на оси NH. Рассмотрим по-

дробнее расположение центров этих сфер от-

носительно пирамиды.

Центр описанн ой сферы одинаково уда-

лён от вершин основания и поэтому ле-

жит на прямой, перпендикулярной основа-

нию и проходящей через центр основания,

т. е. на высоте NH пирамиды или на её про-

должении за точку H. Если продолжени е

высоты NH пересекает сферу в точке M , то MN — диаметр сферы

и, следовательно, ∠MA

N = 90

◦

. Центр описанной сферы совпадает

с точкой H, когда ∠NA

H = 45

◦

, он лежит на высоте пирамиды или

на её продолжении в зависимости от того, будет ли ∠NA

H больше или

меньше 45

◦

Введём обозначения: MN = 2R, A

=a, NA

=b, NH =h, A

H = R

∠NA

H = . Учитывая, что A

H — высота прямоугольного треугольни-

ка A

MN, проведённая к его гипотенузе, получим соотношения, ко-

торыми удобно пользоваться при решении задач на вычисление эле-

ментов правильной пирамиды: b

= 2Rh, R

= (2R − h)h, a = 2R

sin

Рис. 36

b = 2R sin , h = b sin a, R

= b cos .

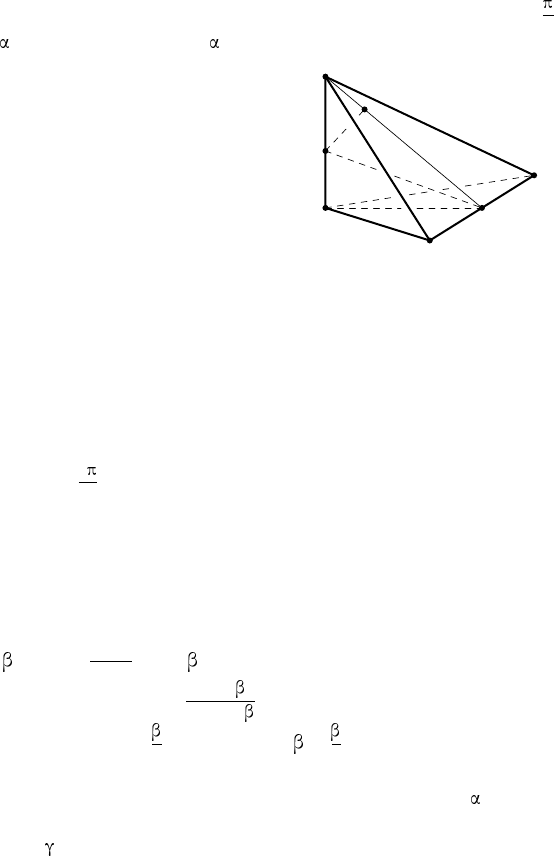
Центр сферы, вписанной в правиль-

ную пирамиду, всегда лежит внутри

пирамиды, на её высоте. Пусть NK —

апофема правильной n-угольной пира-

миды NA

. . . A

(на рис. 36 изобра-

жена лишь час ть пирамиды). Поскольку

NK ⊥A

и N H ⊥A

, то ребро A

перпендикулярно плоскости NHK в силу

теоремы о двух перпенд ик улярах. Прове-

дём биссектрису угла HKN, она пересе-

чёт высоту NH в точке, которую обозна-

чим через O. Докажем, что O — центр сферы, вписанной в пирамиду.

Проведём перпендикуляр OL к апофеме N K. Тогда OL = OH, и сфе-

ра радиусом OL с центром O касается основания пирамид ы в точке H.

Она касается также боковой грани NA

. Это следует из того, что

OL ⊥A

и OL ⊥NK. Значит, плоскость NA

перпендикулярна ра-

диусу OL и касается сферы в точке L. Поскольку при поворотах вокруг

оси N H на углы

(k = 1, 2, . . . , n − 1) грань NA

пирамиды пе-

реходит во все другие грани, а точка O остаётся неподвижной, то рас-

стояния от точки O до всех граней пирамиды одинаковы и р авны OL,

т. е. сфера с центром O и радиусом OH является вписанной в пира-

миду. Центр O сферы есть точка пересечения высоты NH пирамиды

и биссектрисы угла NKH (угол NKH — линейный угол двугранного

угла при основании пирамиды). Введём обозначения: NH = h, OH = r,

∠HKN = , тогда

h −r

= cos (так как KO — би ссе ктри са угла тре-

угольника HKN ), откуда r =

h cos

1 + cos

. Радиус r можно вычислить так-

же по формуле r = HK tg

, или r = h ctg tg

Форма п равил ьной n-угольной пирамиды определяется заданием од -

ного из её угловых элементов. Например, если и звес тен угол наклона

бокового ребра к плоскости основания, то можно вычислить величину

плоского угла при вершине пирамиды, или отношение высоты пира-

миды к стороне основания и т. д. В таком случае говорят, что пирамида

определена с точностью до подобия. Если задан один из углов, кроме

того, один лин ейн ый элемент пирамиды, то можно вычислить любые

другие её элементы.

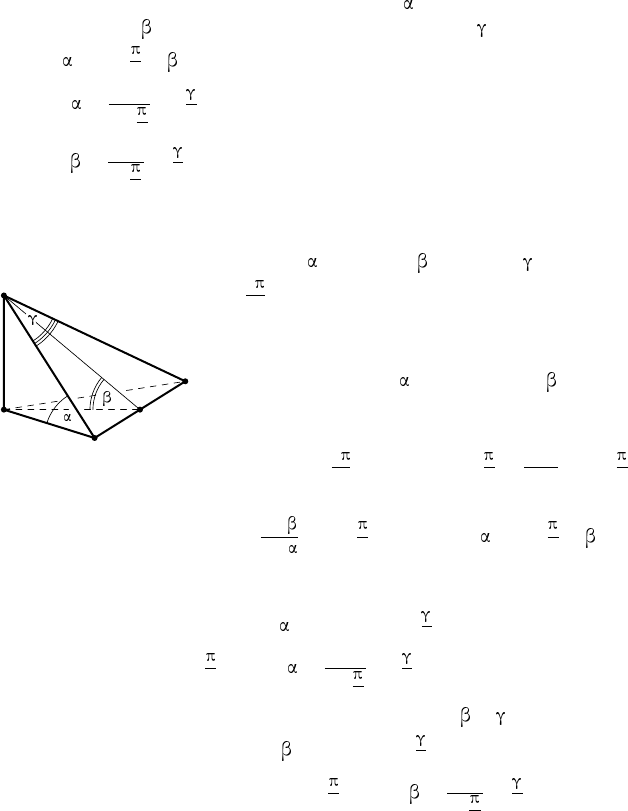
При решении задач о правильной пирамиде часто приходится на-

ходить зависимости между некоторыми её углами. Приведём примеры.

П р и м е р 1. Боковое ребро правильн ой n-угольной пирамиды на-

клонено к плоскости основания под углом , двугранный угол при

основании равен , плоский угол при вершине равен . Докажите, что

a) tg = cos

tg ,

б) cos =

sin

в) cos =

Р е ш е н и е. Пусть AB — сторона основания правильной n-угольной

пирамиды, N H — высота пирамиды, NK — её апофема (рис. 37). Тогда

Рис. 37

∠NAH = , ∠NKH = , ∠ANB = и ∠AHB =

. Прямоугольные треугольники ANH

и HNK имеют общий катет N H. Обозначив

NH = h, имеем:

AH = h ctg , HK = h ctg .

Так как HK — высота, медиана и биссек-

триса равнобедренного треугольника AHB

и ∠ AHB =

, то ∠AHK =

= cos

Следовательно,

ctg

= cos

, или tg = cos

tg .

Из прямоугольных треугольников AN H и ANK, имеющих общую

гипотенузу AN = b, находим

AH = b cos , AK = b sin

А так как AK = AH sin

, то cos =

sin

Аналогично найдём соотношение между углами и . Имеем:

HK = l cos , AK = l tg

где l = KN. А так как HK = NK ctg

, то cos =

Формулы а), б), в) находят при ме нен ие при решении более сложных

задач. Жел ательно научиться их быстро выводить для данных значе-

ний n.