Готман Э.Г. Стереометрические задачи и методы их решения
Подождите немного. Документ загружается.

Э. Г. Готман
Стереометрические задачи
и методы их решения
Москва
Издательство МЦНМО, 2006

УДК 514.113
ББК 22.151.0
Г73
Готман Э. Г.
Г73 Стереометрические задачи и методы их решения. — М.:
МЦНМО, 2006. — 160 с.: ил.
ISBN 5-94057-263-4
Книга содержит задачи по стереометрии, предназначенные для до-
полнительного образования учащихся старших классов. Она может так-
же служить пособием для подготовки к математичес ким олимпиадам
и к вступительным экзаменам по математике в высшие учебные заве-
дения.
ББК 22.151.0
Эдгар Готлибович Готман
СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
И МЕТОДЫ ИХ РЕШЕНИЯ
Редактор Семенов А. В.
Подписано в печать 20.09.2006 г. Формат 60 × 90
1
/
16
. Бумага офсетная № 1.
Печать офсетная. Печ. л. 10. Тираж 2000 экз. Заказ №
Издательство Московского центра непрерывного математического образова-
ния. 119002, Москва, Большой Власьевский пер., д. 11. Тел. 241–74–83.
Отпечатано с готовых диапозитивов в ФГУП «Полиграфические ресурсы».
Книги издательства МЦНМО можно приобрести в магазине «Математическая
книга», Большой Власьевский пер., д. 11. Тел. 241–72–85. E-mail: biblio@mccme.ru
ISBN 5-94057-263-4
c
Готман Э. Г., 2006.
c
МЦНМО, 2006.
Оглавление
Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Глава 1. Многогранники 6
§ 1. Призма, паралле леп ип ед, куб . . . . . . . . . . . . . . . . . . . . 17
§ 2. Пирамид а, усечённая пирамида . . . . . . . . . . . . . . . . . . . 19
Глава 2. Тела вращения 24
§ 3. Цилинд р, конус, усечённый конус . . . . . . . . . . . . . . . . . 28
§ 4. Комбинация круглых тел . . . . . . . . . . . . . . . . . . . . . . 30
§ 5. Касание круглых тел . . . . . . . . . . . . . . . . . . . . . . . . . 31
Глава 3. Векторный метод 33
§ 6. Аффинные задачи . . . . . . . . . . . . . . . . . . . . . . . . . . 42
§ 7. Метри чес кие зад ачи . . . . . . . . . . . . . . . . . . . . . . . . . 45
Глава 4. Метод координат 50
§ 8. Вычисл ен ие расстояний и углов . . . . . . . . . . . . . . . . . . 57
§ 9. Многогр анни ки и сфера . . . . . . . . . . . . . . . . . . . . . . . 58
Глава 5. Наибольшие и наименьшие значения 60
§ 10. Примен ени е элем ентарных методов . . . . . . . . . . . . . . . . 67
§ 11. Примен ени е произ водной . . . . . . . . . . . . . . . . . . . . . . 70
Глава 6. Треугольник и тетраэдр 73
§ 12. Метрич еск ие соотноше ния в тетраэдре . . . . . . . . . . . . . . 76
§ 13. Прямоугольный тетраэдр . . . . . . . . . . . . . . . . . . . . . . 79
§ 14. Ортоцентрич ес кий тетраэдр . . . . . . . . . . . . . . . . . . . . 82
§ 15. Равногранный тетраэдр . . . . . . . . . . . . . . . . . . . . . . . 83
Глава 7. Комбинации геометрических тел 87
§ 16. Призмы и пирам иды . . . . . . . . . . . . . . . . . . . . . . . . 87
§ 17. Правильная пирамид а и сфера . . . . . . . . . . . . . . . . . . 88
§ 18. Правильная пирамид а и сфера, касающаяся всех её рёбер . . 95
§ 19. Разные задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
Ответы, указания, решения . . . . . . . . . . . . . . . . . . . . . . . 105
Обозначения и формулы . . . . . . . . . . . . . . . . . . . . . . . . . 159
3
Предисловие
Задачи по стереометрии — прекрасные упражнения, способствую-
щие развитию пространственных представлений, умения логически
мыслить, сп особствующие более глубокому усвоению всего школьно-
го курса математики.
Решение стереометрической задачи чаще всего сводится к решению
планиметрических задач. Поэтому, решая задачи по стереометрии, всё
время приходи тся возвращаться к п лани метр ии, повторять теоремы,
вспоминать формулы, необходимые для решения. При решении стерео-
метрических задач ещё в большей мере, чем в планиметрии, ис поль-
зуются средства алгебры и тригонометрии, применяются векторный
и координатный методы, дифференцирование и интегрирование. Таким
образом, стереометрические задачи способствуют творческому овладе-
нию всей совокупностью математических знаний.
Настоящее пособие является продолжением книги автора «Задачи
по планиметрии и методы их решения» (М.: Просвещение, 1996). Тем
не менее, пользоваться настоящим п особием можно и тем, кто не зна-
ком с книгой по планиметрии, здесь нет ссылок на ту книгу. По сво-
ей структуре книга «Задачи по стереометрии» несколько отличается
от предыдущей. Классификация задач в основном проводится не по ме-
тодам решения, а по содержанию, по характеру геометрич еск их фигур.
Книга предназначена главным образом для учащихся старших клас-
сов, желающих углубить свои зн ания по математике, и может служить
пособием для подготовки к математическим олимпиадам и к вступи-
тельным экзаменам по матем атике в высшие учебные заведения. Книга
будет полезна также учителям математики, руководителям математи-
ческих кружков, студентам педагогических институтов.
Данное пособие содержи т много довольно п ростых задач, по трудно-
сти мало отличающихся от задач, помещённых в школьных учебниках.
Особое внимание уделено классификации задач. Для решения предла-
гаются не разрозненные задачи, а серии задач, связанных между собой
по содержанию и методам решения. Задачи расположены в порядке
возрастания трудности, так что решение первых более простых задач
помогает находить решения следующих за ними.
В начале каждой главы рассказано о методах решения, приводятся
решения типичных задач, даны необходимые теоретические сведения.
Главы 1 и 2 содержат задачи о многогранниках и телах вращения.
В главах 3 и 4 собраны задачи, для решения которых целесообразно
4
пользоваться векторным и координатным методами. Глава 5 посвяще-
на геометрии тетраэдра. При решении задач этой главы рекомендуется
использовать, где это возможно, аналогию между треугольником и тет-
раэдром. Глава 6 содержит разнообразные задачи на отыскание наи-
больших и наименьших значений геометрических величи н. При этом
особо выделены задачи, решаемые элементарными средствами, без при-
менения производной. В последнюю главу 7 включены задачи на ком-
бинацию многогранников и тел вращения. Среди них много задач по-
вышенной трудности.
Ко всем задачам на вычисление даны ответы. Большинство трудных
задач снабжено указаниями или краткими решениями.
5
Г л а в а 1
Многогранники
В курсе стереометрии особую роль играет чертёж. Если в плани-
метрии всегда есть возможность выполнить точный чертёж, то в сте-
реометрии изображение на плоскости не может быть точной копией
оригинала — пространственной фигуры. Тем не менее, следует старать-
ся чертёж выполнить так, чтобы по нему можно было получить ясное
представление об оригинале.
Существуют различные способы изображения пространственных
фигур на плоскости. В школьной практике пользуются методом па-
раллельного проецирования.
При и зображении многогранни ков часто удобно пользоваться каби-
нетной проекцией, известной из курса черчения.
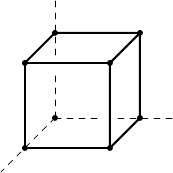
A
B
CD
A
1
B
1
C
1
D
1
Рис. 1
На рис. 1 в кабинетной проекции изображён
куб. Изображениями двух граней, параллельных
плоскости чертежа, являются квадраты. Каждая
из остальных граней куба изображается в виде
параллелограмма с острым углом 45
◦
, у которо-
го одна сторона совпадает со стороной квадрата,
а смежная с ней вдвое короче.
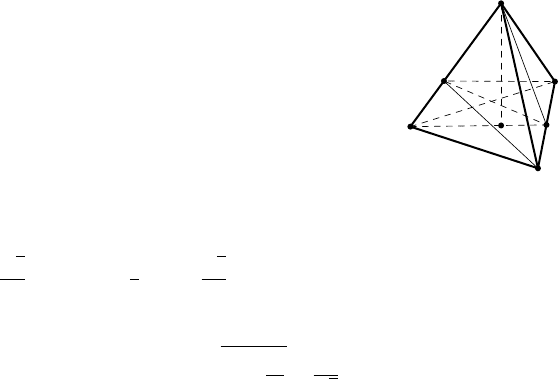
На рис. 2 дано изображение правильной тре-
угольной пирамиды NABC. Плоскость AKN, где
NK — апофема пирамиды, параллельна плоско-
сти чертежа, поэтому отрезки AN и KN, как
и угол NAK наклона бокового ребра к плоскости основания, изобра-
жаются без искажений.
В кабинетной проекции удобно изображать прямоугольный паралле-
лепипед, прямую призму, правильную пирамиду и другие простейш ие
многогранники.
Конечно, чертёж может быть выполнен в произвольной параллель-
ной проекции. Важно лишь, чтобы чертёж был верным, наглядным
и не слишком трудным для выполнения.
В данном пособии стереометрические задачи на построение, задачи
на проекционном чертеже, приёмы и методы решен ия которых подробно
описаны в учебной литературе, специально не рассматриваются. Одна-
ко имеется ряд комбинированных задач на построение сечений с после-
дующими вычислениями.
6
В главу 1 включены в основном задачи на доказательство и вычис-
ление.
Для решения задач на доказательство чаще всего применяется гео-
метрический м етод, используются теоремы планиметрии и стереомет-
рии, доказываемое утверждение устанавливается с помощью логи че-
ских рассуждений. При этом часто приходится выполнять различные
дополнительные построения.
В некоторых случаях кроме изображения пространственной фигу-
ры полезно сделать плоский чертёж, представляющий собой какое-либо
сечение данного тела, развёртку его поверхности или проекцию на неко-
торую плоскость.
Основным методом р еше ния стереометрических задач на вычисле-
ние является алгебраический. Используются как ал гебраи чес ки е, так
и тригонометрические тождества и уравнения.
Необходимо обращать внимание на начальную стадию решения каж-
дой задачи — анализ, когда намечается ход решения, причём нередко
правильный путь находится не сразу, а после ряда неудачных попыток.
Выполнив чертёж , следует внимательно изучить связи между данн ыми
и неизвестными элементами фигуры и попытаться связать их ц епоч кой
промежуточных величин.
Рассмотрим конкретные примеры.
П р и м е р 1. Высота пр авильной треугольной пирамиды равна сто-
роне её основания, длина которой a. Найти площадь сечения пирами-
A
B
C
N
H
K
L
Рис. 2
ды плоскостью, проходящей через сторону осно-
вания перпендикулярно противоположному ребру.
Р е ш е н и е. Пусть NH — высота данной пира-
миды NABC и BCL — сечение плоскостью, пер-
пендикулярной ребру AN (рис. 2). Поскольку пи-
рамида правильн ая, то H — центр правил ьного
треугольника ABC. Треугольник BCL — равно-
бедренный. Чтобы найти его высоту KL, доста-
точно последовательно вычислить длины отрез-
ков AK, AH и AN.
Треугольник ABC — правильный и AB = a,
и мы легко находим:
AK =
√
3
2
a, AH =
2
3
AK =
√
3
3
a (радиус описанной окружности).
По теореме Пифагора из треугольника AHN получаем:
AN =
r
a
2
+
a
2
3
=
2
√
3
a.
7
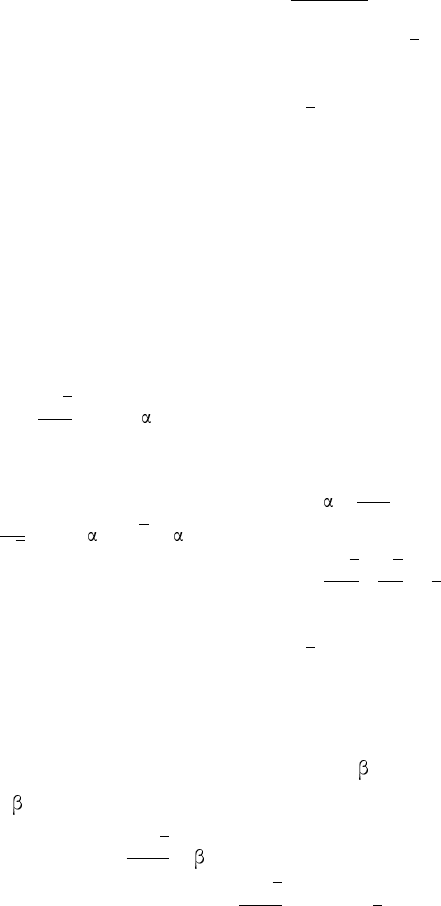
Далее, выразив двумя способами площадь треугольника AKN , по-
лучим:
KL =
AK · NH
AN
.
Подставив найденные значения, найдём: KL =
3
4
a. Следовательно, пло-
щадь треугольника BCL равна
S =
3
8
a
2
.
При решении данной задачи мы использовали метод, который назы-
вают п оэтапно-вычислительным или ме тодом прямого счёта. Он явля-
ется разновидн остью алгебраического метода. При поэ тапном решении
последовательно вычисляются промежуточные величины, с помощью
которых искомые величины связываются с данными.
После того, как задача решена, следует убедиться в правильности
решения и попытаться найти более короткий путь, ведущий к решению
задачи.
Просматривая предл оженное реш ен ие, можно заметить, что высо-
ту KL треугольника BCL можно вычислить по-другому. Отрезок KL
является катетом прямоугольного треугольника AKL, гипотенуза его
AK =
a
√
3
2
, угол наклона бокового ребра AN к плоскости основа-
ния можно найти. Таким образом, приходим к такому решению за-
дачи.
Из треугольника AHN находим tg =
NH
AH
, а так как N H = a и AH =
=
a
√
3
, то tg =
√
3 и = 60
◦
. Из тре угольника AKL имеем:
KL = AK sin 60
◦
=
a
√
3
2
·
√
3
2
=
3
4
a.
Следовательно,
S =
3
8
a
2
.
Это решение можно ещё немного упростить, если заметить, что тре-
угольник BCL ес ть ортогональная проекция треугольника ABC на
плоскость BCL, и поэтому
S = S
ABC
· cos ,
где = ∠AKL — линейный угол двугранного угла между плоскостями
BCL и ABC.
Так как S =
a
2
√
3
4
и = 30
◦
, то
S =
a
2
√
3
4
cos 30
◦
=
3
8
a
2
.
8
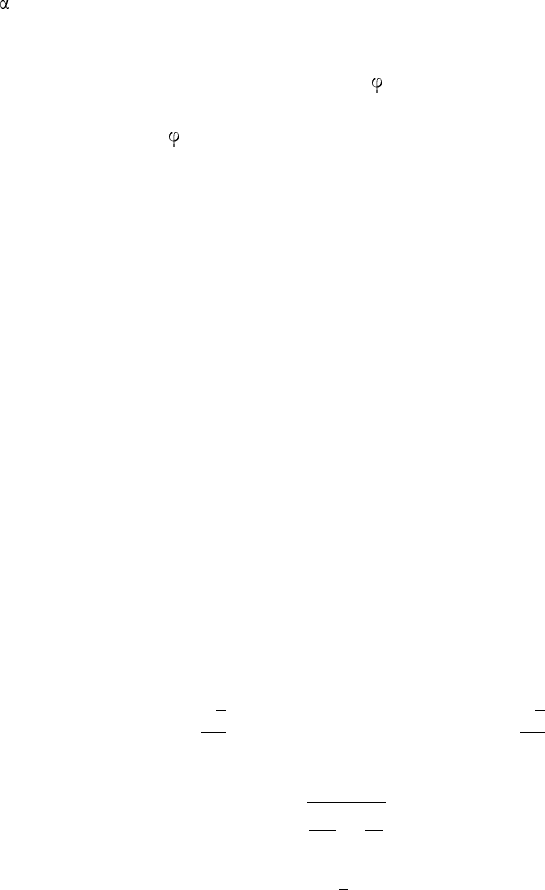
Решая задачу вторым спос обом, мы узнали свойство правильной
треугольной пирамиды: есл и её высота равна стороне основания, то бо-
ковое ребро пир ами ды наклонено к плоскости основания под углом
= 60
◦
.
При решении задачи третьим способом мы использовали теорему
о площади ортогональной проекции многоугольника на плоскость
S
пр
= S · cos ,
где S — площадь данного многоугольника, S
пр
— площадь его проек-
ции на плоскость, — угол между плоскостью данного многоугольника
и плоскостью его проекции.
Доказательство этой теоремы можно найти в учебных пособиях
по геометрии. Формула находит применение при решении некоторых
задач на вычисление площадей поверхностей пирамид и площадей се-
чений многогранников (см. пример 6).
Теперь рассмотрим задачу, похожую на предыдущую.
П р и м е р 2. Через сторону основания правильной треугольной пи-
рамиды проведена плоскость перпендикулярно противоположному бо-
ковому ребру. Сторона основания равна a, секущая плоскость делит
боковое ребро в отношении 3 : 2, считая от вершины пирамиды. Найти
боковое ребро и площадь боковой поверхности пирамиды.
Р е ш е н и е. Воспользуемся рис.
2 и уже введёнными обозначения-
ми. Из треугольника ABN длину бокового ребра AN прямым счётом
найти не удаётся, но м ожно применить метод составления уравнений,
хорошо известный из курса алгебры.
Обозначим AL = 2x, LN = 3x. Тогда AN = BN = 5x.
Боковое ребро AN пе рп енд икулярно плоскости BCL, поэтому оно
перпендикулярно прямой BL, зн ачит, треугольники ABL и BLN — пря-
моугольные. Выразим двумя способами их общий катет BL, пользуясь
теоремой Пифагора:
BL
2
= a
2
− 4x
2
и BL
2
= 25x
2
− 9x
2
.
Получим уравнение:
16x
2
= a
2
− 4x
2
,
откуда 20x
2
= a
2
, x =
√
5
10
a, а так как AN = 5x, то AN =
√
5
2
a.
Все другие элементы пирамиды теперь можно найти прямым счётом.
Из треугольника BKN , согласно теореме Пифагора, имеем:
KN =
r
5a
2
4
−
a
2
4
= a.
Следовательно,
S
бок
=
3
2
a
2
.
9

Решение стереометрической задачи иногда упрощается, если соста-
вить не алгебраическое, а тригонометрическое уравнение. Рассмотрим
пример.
П р и м е р 3. Основанием пирамиды служит ромб, две боковые гра-
ни которого перп енд ик улярны плоскости осн ования. Под каким углом
наклонены к плоскости основания две другие грани, если площадь бо-
ковой поверхности пирамиды вдвое больше площади его основания?
Р е ш е н и е. Пусть NABCD — данная пирамида, грани ADN и CDN
которой перпендикулярны плоскости основания (рис. 3). Поскольку
N
C
K
BA
D
Рис. 3
ABCD — ромб и AD = CD, то прямоугольные треугольники ADN
и CDN равны, значит, AN = CN. Треугольники ABN и BCN также
равны (три стороны одного треугольника равны трём сторонам друго-
го). Проведём DK ⊥ BC, тогда NK ⊥ BC по теореме о трёх перпенди-
кулярах. Следовательно, DKN — линейный угол двугранного угла при
ребре BC.
Для нахождения угла DKN составим уравнение. Пусть ∠DKN = x.
Введём ещё два вспомогательных параметра: AB = a и DK = h. Из тре-
угольника DKN имеем:
DN = h · tg x, KN =
h
cos x
.
Площадь боковой поверхности п ир амид ы равна S
бок
= 2S
ADN
+ 2S
BCN
,
или
S
бок
= AD · DN + BC · KN.
Подставив в это равенство значения AD, DN и KN, получим:
S
бок
= ah
tg x +
1
cos x
.
Согласно условию задачи S
бок
= 2S
осн
, но S
осн
= ah, следовательно,
tg x +
1
cos x
= 2.
10
