Готман Э.Г. Стереометрические задачи и методы их решения

Подождите немного. Документ загружается.

чённого конуса и радиус сферы, если образующая усечённого конуса

равна l.

92. В сферу радиуса R вписан усечённый конус, образующая кото-

рого равна R

√

2, а угол наклона её к плоскости нижнего основания

равен . Найдите площадь полной поверхности усечённого конуса.

93. В сферу радиуса R вписан усечённый конус, образующая которо-

го сос тавляет с плоскостью основания угол . Угол между диагоналями

в осевом сечении конуса, обращённый к основанию, равен . Найдите

площадь осевого сечения конуса.

94. В сферу радиуса R вписан усечённый конус, высота которого

равна h. Диагонали осевого сечения конуса перпендикулярны. Найдите

объём усечённого конуса. Имеет ли задача решение, если а) h =

б) h =

§5. Касание круглых тел

95. Три шара, радиусы которых равны 2a, 3a и 3a, касаются попарно

внешним образом. Найдите радиус сферы, касающейся каждого из них

внутренним образом, если её центр и центры данных трёх шаров лежат

в одной плоскости.

96. Три шара лежат на плоскости и попарно касаются друг друга.

Расстояние между точками касания их с плоскостью равны a, b и c.

Найдите радиусы шаров.

97. Внутри сферы расположены ч етыре шара одного и того же ра-

диуса r. Каждый из них касается трёх других и сферы. Найди те радиус

сферы.

98. Четыре одинаковых шара радиуса r лежат на плоскости. Центры

их находятся в вершинах квадрата со стороной 2r. Пятый шар того же

радиуса касается всех четырёх. Найдите расстояние от центра пятого

шара до плоскости.

99. На основании конуса лежат три шара радиуса r, каждый из ко-

торых касается двух др угих и боковой поверхности конуса. Угол при

вершине осевого сечения конуса равен 60

◦

. Найдите радиус основания

конуса.

100. На основании конуса лежат два шара радиуса r. На них лежит

четвёртый шар того же радиуса. Каждый из этих четырёх шаров ка-

сается боковой поверхности конуса и трёх других шаров. Найдите угол

наклона образующей к плоскости основания и высоту конуса.

101. Внутри цилиндра лежат два шара радиуса 2a и один шар ради-

уса a так, что каждый шар касается двух других, нижнего основания

цилиндра и его боковой поверхности. Найдите радиус основания ци-

линдра.

102. На плоскости лежат три ш ара, попарно касающихся друг друга.

Радиусы их равны r, 3r и 3r. Четвёртый шар касается первых трёх

и той же плоскости. Найдите радиус четвёртого шара.

103. Три шара, ради усы которых равны 3, 1 и

, попарно касаются

друг друга и некоторой плоскости. Четвёртый шар касается первых

трёх и той же плоскости. Найдите радиус четвёртого шара.

104. Два шара одного радиуса и два другого лежат на плоскости

и каждый касается трёх других. Найдите отноше ние радиуса большего

шара к радиусу меньшего.

105. Четыре шара расположены так, что каждый из них касается

трёх остальных. Радиусы трёх шаров равны R, радиус четвёртого ша-

ра r. Найдите радиус пятого шара, касающегося всех четырёх шаров,

если R = 6 и r = 1.

Г л а в а 3

Векторный метод

При решении геометрических задач, кроме традиционных методов

с использованием алгебры и тригонометрии, могут применяться и дру-

гие методы, в частности, векторный. Умени е пользоваться векторами

требует опред елё нн ых навыков. Надо научиться переводить геометри-

ческие утверждения на векторный язык, а также, наоборот, вектор-

ные соотношения истолковать геометрически. Вектор ный метод, как

и любой другой, применим не всегда. Умение заранее предвидеть, го-

дится ли он для решения конкретной задачи или нет, вырабатывается

опытом.

Естественно вначале научиться применять векторы к решению пла-

ниметрических задач. Такие задачи можно найти в книге автора «За-

дачи по планиметрии и методы и х решения» и других учебных посо-

биях.

В настоящей главе помещены планиметрические задачи, в §6 — з ада-

чи на пар алле льность, принадле жность трёх точек одной прямой и че-

тырёх точек одной плоскости, на отношение отрезков параллельных

прямых. Такие задачи называют аффинными. Для и х решения исполь-

зуются операции сложения и вычитания векторов, умножения векто-

ра на число и их свойства. Задачи на вычисление расстояний, углов

и некоторые другие, помещённые в § 7, не могут быть решены толь-

ко с помощью указанных операций и требуют применения скалярного

произведения векторов. Такие задачи называются метрическими.

Приведём основные векторные соотношения и формулы, на которых

основано решение задач.

1) Для любых трёх точек A, B, C имеет место равенство:

AB + BC = AC (правило треугольника).

2) Для любых трёх точек A, B и O выполняется равенство:

AB = OB − OA (правило вычитания векторов).

3) Для того, чтобы точка C лежала на прямой AB, необходимо и до-

статочно, чтобы существовало такое число k, что

AC = k · AB.

Из этого равенства следует, что

= k.

4) Пусть A и B — две различные точки прямой и C — точка этой

прямой такая, что

= k. Докажем истин ность формулы:

OC =

OA + k · OB

1 + k

где O — произвольная точка.

Заметим, что k 6= −1, иначе было бы AC = −CB, или AC + CB = 0 ,

т. е. AB = 0 . Но это невозможно, поскольку A и B — различные точки.

Пусть

= k или AC = k ·CB. Пользуясь правилом вычитания век-

торов, получим:

OC − OA = k(OB − OC),

или

OC + kOC = OA + kOB,

откуда

OC =

OA + kOB

1 + k

Эту формулу называют формулой деления отрезка в данном отно-

шении.

Если C — середина отрезка AB, то k = 1 и OC =

(OA + OB).

5) Четырёхугольник ABCD является параллелограммом тогда и

только тогда, когда выполняется одно из следующих равенств: AD =

= BC, AC = AB + AD, OA + OC = OB + OD, где O — произвольная точ-

ка пространства.

6) Если векторы a и b неколлинеарны, то для любого вектора c ,

лежащего с a и b в одной плоскости, существует единственная пара

чисел x и y таких, что

c = x a + y b .

7) В пространстве для каждого вектора p существует единственное

разложение по трём данным некомпланарным векторам a , b , c :

p = x a + y b + z c

(x, y, z — од нозн ачно определ ён ные чис ла).

В частности, если x a + y b + z c = 0 , то x = y = z = 0.

8) Пусть точки A, B, C не лежат на одной прямой, тогда для того,

чтобы точка D лежала в плоскости ABC, необходимо и достаточно,

чтобы существовала такая пара чисел и , что

CD = CA + CB.

Покажем, как доказать известную теорему о медианах треугольника

векторным методом.

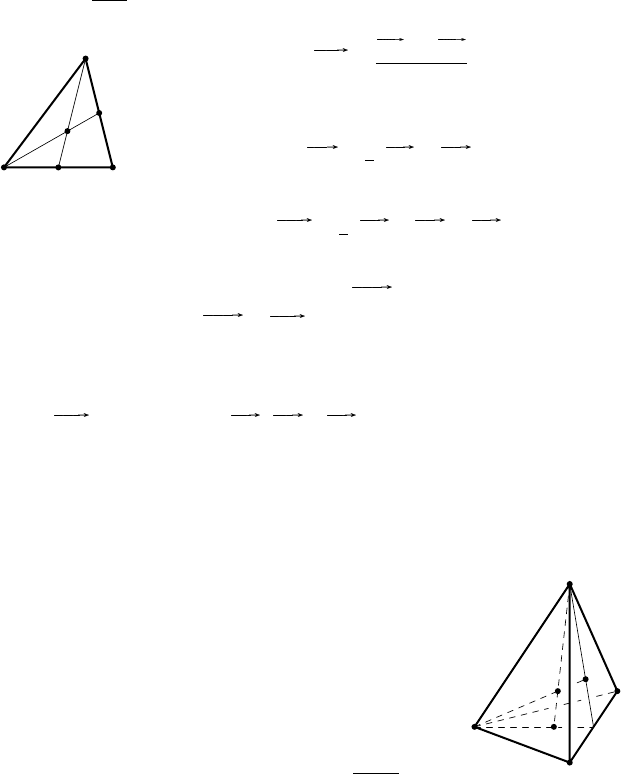
П р и м е р 1. Доказать, что медианы треугольника пересекаются

в одной точке, которая делит каждую из них в отношении 2 : 1, счи-

тая от вершины.

Р е ш е н и е. Возьмём на медиане CD треугольника ABC точку M,

такую, что

= 2 (рис. 15). Согласно формуле деления отрезка в дан-

A B

Рис. 15

ном отношении

OM =

OC + 2OD

где O — произвольная точка пространства. А так

как D — середина отрезка AB, то

OD =

(OA + OB).

Из этих двух равенств след ует, что

OM =

(OA + OB + OC).

Пусть точка M

делит любую из двух других медиан в отношении 2: 1,

считая от вершины. Тогда для вектора OM

аналогично получим тоже

самое выражение, т. е. OM

= OM. Значит, точки M и M

совпадают.

Таким образом, все три медианы треугольника ABC имеют общую точку

M, которая делит каждую из них в отношении 2 : 1, считая от вершины.

Теорема доказана. Попутно мы получили формулу, выражающую

вектор OM через век торы OA, OB и OC, которая верна и в том случае,

когда точка O не лежит в плоскости треугольника и OABC — тетраэдр.

Точка M пересечения медиан треугольника называется его центроидом.

Тетраэдр и ме ет ряд свойств, аналогичных свойствам треугольника.

Отрезок, соединяющий вершину тетраэдра с центроидом противопо-

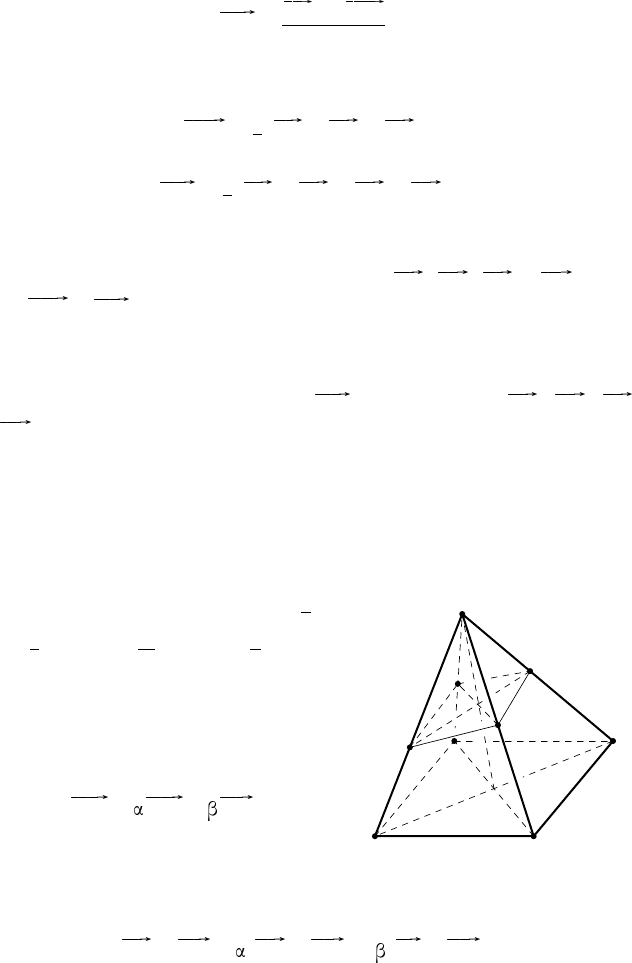
Рис. 16

ложной грани, называют медианой тетраэдра.

Медианы тетраэдра, как и медианы треугольни-

ка, пересекаются в одной точке.

Докажем теорему о медианах тетраэдра тем

же способом, что и предыдущую.

П р и м е р 2. Доказать, что медианы тетра-

эдра пересекаются в одной точке и делятся ею

в отношении 3 : 1, считая от вершины.

Р е ш е н и е. Возьмём на медиане DM

тет-

раэдра ABCD точку M такую, что

D M

= 3

(рис. 16). По формуле деления отрезка в данном

отношении имеем:

OM =

OD + 3OM

где O — любая точка пространства (на рис. 16 не изображена).

Учитывая, что центроид M

треугольника ABC удовлетворяет со-

отношению

(OA + OB + OC),

получим:

OM =

(OA + OB + OC + OD).

Для точки M

, делящей любую из трёх других медиан тетраэдра

ABCD в отношени и 3 : 1, считая от вершины, получим то же самое

выражение (оно симметрично относительно OA, OB, OC и OD). Зна-

чит, OM

= OM и все четыре медианы тетраэдра пересекаются в од-

ной точке M и каждая из н их д ели тся этой точкой в отношен ии 3 : 1,

считая от вершины тетраэдра. Точку M называют центроидом тетра-

эдра.

Формула, выражающая вектор OM через векторы OA, OB, OC

и OD, в дальнейшем находит применение при реш ени и задачи.

Рассмотрим ещё одну аффинную задачу, при решении которой ис-

пользуется теорема о раз ложении вектора и признак принадлежности

четырёх точек одной плоскости.

П р и м е р 3. Основанием пирамиды SABCD служит параллело-

грамм. Проведена плоскость, пересекающая боковые рёбра SA, SB,

Рис. 17

SC, SD пирамиды соответственно в точ-

ках K, L, M, N таких, что SK =

SA,

SL =

SB, SM =

SC, SN =

SD. Най-

ти зависимость между числами k, l,

m и n.

Р е ш е н и е. Согласно условию при-

надлежности четырёх точек K, L, M

и N одной плоскости имеем:

MN = MK + ML.

Представим каждый из векторов,

входящих в это равенство, в виде раз-

ности двух векторов с общим началом

в точке S (рис. 17). Получим:

SN − SM = (SK − SM) + (SL − SM).

Отсюда

SN = SK + SL + SM,

где = 1 − − .

Учитывая условие задачи, предыдущее равенство перепишем так

SD =

SA +

SB +

SC.

Обозначим через O точку пересечения диагонале й параллелограмма

ABCD. Так как O — середина диагоналей AC и BD, то

SA + SC = SB + SD = 2SO.

Значит,

SD =

(SA − SB + SC).

Таким образом, вектор

SD выражен двумя способами через неком-

планарные векторы SA, SB и SC.

В силу единственности разложения вектора получаем числовые ра-

венства:

= −

Отсюда, учитывая, что + + = 1, находим:

−

= 1,

или

k + m = l + n.

Приведём числовой пример. Если плоскость проходит через вер ши-

ну A тетраэдра ABCD и п ере секает его рёбра SB и SD в точках L и N

таких, что SL =

SB, SN =

SD, то k = 1, l = 2, n = 3, следовательно,

m = 2 + 3 − 1 = 4, т. е. SM =

SC.

При решении различных геометрических задач на вычисление длин

отрезков и величин углов, на доказательство геометрических нера-

венств и некоторых других эффективно может быть использовано

скалярное произведение векторов. Напомним его важнейшие с войства.

1) Из опр еде лен ия скалярного произведени я следует, что

a · a = |a |

т. е. скалярный квадрат вектора равен квадрату его дли ны. Следова-

тельно, для нахождения длины отрезка AB может быть использована

формула

= AB

Угол между векторами a и b вычисляется по формуле

cos =

a · b

|a | ·| b |

2) Для любых векторов a и b имеет место неравенство

( a · b )

> a

· b

3) Отрезки AB и CD перпендикулярны тогда и только тогда, когда

AB · CD = 0.

4) Для любых векторов a и b имеет место формула:

( a + b )

= a

+ 2 a · b + b

Для успешного применения векторов полезно знать некоторые ра-

венства, часто используемые при решение задач. В частности, следу-

ющие.

5) Для любых векторов a , b , c выполняется равенство:

( a + b + c )

= a

+ b

+ c

+ 2 a · b + 2 b · c + 2 c · a .

6) Для любых трёх точек A, B и C:

+ AC

− BC

= 2AB · AC

(теорема косинусов).

7) Для любых четырёх точек A, B, C, D:

+ BC

− AC

− BD

= 2AB · CD.

Доказательство этого равенства несложно. Век торы BC и BD в ле-

вой части представим в виде разности двух векторов, отложенных от

точки A. Получим:

+ BC

−AC

−BD

= AD

+ (AC −AB)

− AC

−(AD −AB)

= 2AB · AD − 2AB · AC = 2AB · (AD − AC) = 2AB · CD.

Доказанное равенство является обобщением равенства 6), которое

вытекает из него при совпадении точек D и A.

Приведём пр им еры метрических задач, при решении которых целе-

сообразно пользоваться скалярным умножением векторов.

П р и м е р 4. Доказать, что длина медианы m

треугольника ABC

выражается через длины его сторон формулой:

+ b

−

Р е ш е н и е. Пусть CD — медиана треугольника ABC (см. рис. 15).

Тогда

CD =

(CA + CB).

Вычислив скалярный квадрат вектора CD, получим:

+ b

+ 2CA · CB).

Скалярное произведение векторов CA и CB найдём, используя вектор-

ное равенство

AB = CB − CA.

Отсюда c

= a

+ b

− 2CA · CB,

2CA · CB = a

+ b

− c

Следовательно,

(2a

+ 2b

− c

или

+ b

−

Задачу нетрудно решить и элементарными способами. Например,

можно достроить треугольник до параллелограмма и применить теоре-

му о сумме квадратов его диагоналей. Однако аналогичную задачу для

тетраэдра предпочтительнее решать векторным методом, что не требу-

ет дополнительных построений и громоздких вычислений.

П р и м е р 5. Выразить длину медианы DM

тетраэдра ABCD че-

рез длины его рёбер.

Р е ш е н и е. Длина рёбер тетраэдра ABCD обозначим так: AD = a,

BD = b, CD = c, BC = a

, CA = b

, AB = c

(см. рис. 16).

Так как M

— центроид треугольника ABC, то

(DA + DB + DC)

(см. пример 1).

Возведём это равенство в квадрат и получим:

+ b

+ c

+ 2DA · DB + 2DA · DC + 2DB · DC).

Так же, как при решении предыдущей задачи, запишем равенство

AB = DB − DA.

Вычислив скалярный квадрат, получим

= a

+ b

− 2DA · DB,

откуда

2DA ·DB = a

+ b

− c

Аналогично найдём, что 2DA · D C = a

+ c

− b

, 2DB · DC = b

+ c

− a

. Подставив значения скалярных произведений в исходное ра-

венство, получим формулу

+ b

+ c

−

+ b

+ c

выражающую длину m

медианы DM

тетраэдра через длины его

рёбер.

Для решения задачи был выбран базис, состоящий из трёх неком-

планарных векторов DA, D B и DC. Затем вектор DM

, длину которого

требовалось найти, мы разложили по этому базису. После чего вычис-

лили скалярный квадрат вектора DM

При векторном решении задач на вычисление углов поступают ана-

логично. Прежде всего, искомый угол между прямыми заменяют углом

между векторами, которые параллельны данным прямым. Затем эти

векторы выражают через базисные векторы и, пользуясь определением

скалярного произведения векторов, находят угол.

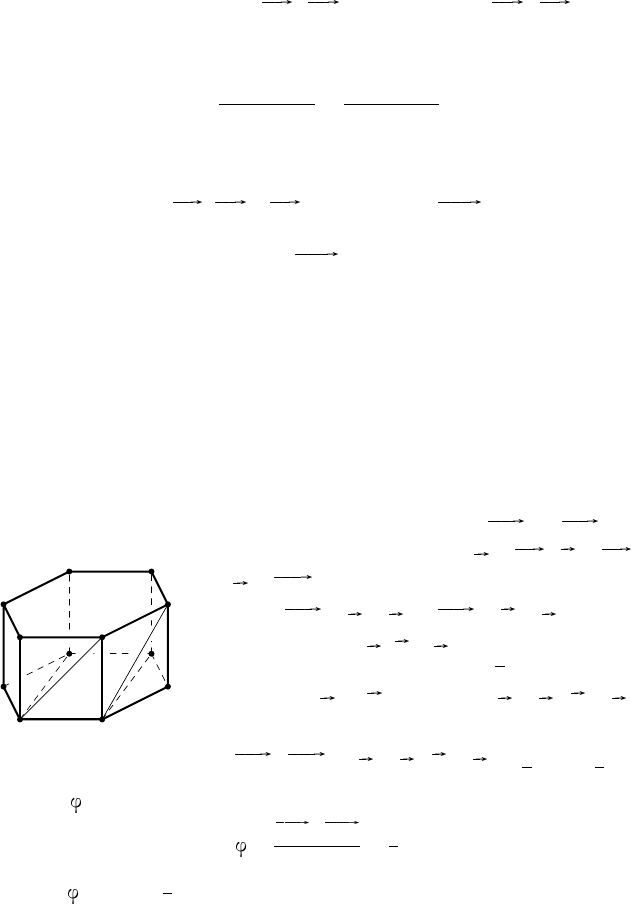
П р и м е р 6. Боковые грани правильной шестиугольной призмы —

квадраты. Найти величину угла между скрещивающи ми ся диагоналя-

ми смежных граней призмы.

Р е ш е н и е. Пусть ABCDEF A

— правильная шести-

угольная призма (рис. 18). Требуется найти угол м ежд у прямыми AB

A B

Рис. 18

и BC

. Разложим векторы AB

и BC

по

некомпланарным векторам a = AB, b = BC

и c = BB

. Получим:

= a + c , BC

= b + c .

Длина векторов a , b и c одинаковы, примем

их за 1, тогда AB

= BC

√

2. Угол между

векторами a и b равен 60

◦

, a ⊥ c , b ⊥ c .

Следовательно,

· BC

= ( a + c )( b + c ) =

+ 1 =

Пусть — угол между прямыми AB

и BC

, тогда

cos =

· BC

Итак, = arccos

Векторные решен ия часто значительнее проще и эффективнее ре-

шений, полученных элементарными средствами, и отличаются большей

общностью.