Готман Э.Г. Стереометрические задачи и методы их решения
Подождите немного. Документ загружается.

309. V =
16
3
R
3
(1 − cos ) cos
2
, V
max
=
64
81
R
3
при = arccos
2
3
.
310. Два решени я: 15
◦
и 75
◦
.
311.
h
1 + ctg
2
. У к а з а н и е. Воспользуйтесь соотношениями
r
h −r
=
= cos и cos = tg
2
, где r — радиус вписанной сферы и — величина
двугранного угла при основании пирамиды.
312.
8
5
b
2
. У к а з а н и е. Воспользуйтесь результатом предыдущей
задачи. Устан овите, что tg
2
=
1
2
и sin =
4
5
. Площадь боковой поверх-
ности пирамиды найдите по формуле S
бок
= 2b
2
sin .
313. 2 с м. У к а з а н и е. Пусть — угол наклона бокового ребра пи-
рамиды к плоскости её основания. Тогда h = 2R sin
2
. Вычислив sin ,
найдите cos ( — величина двугранного угла при основании). Затем
воспользуйтесь формулой r =
h cos
1 + cos
.
314. r = d tg
2
, r =
d
“
1 + tg
2
”
2 cos
. 315.
13
12
a.
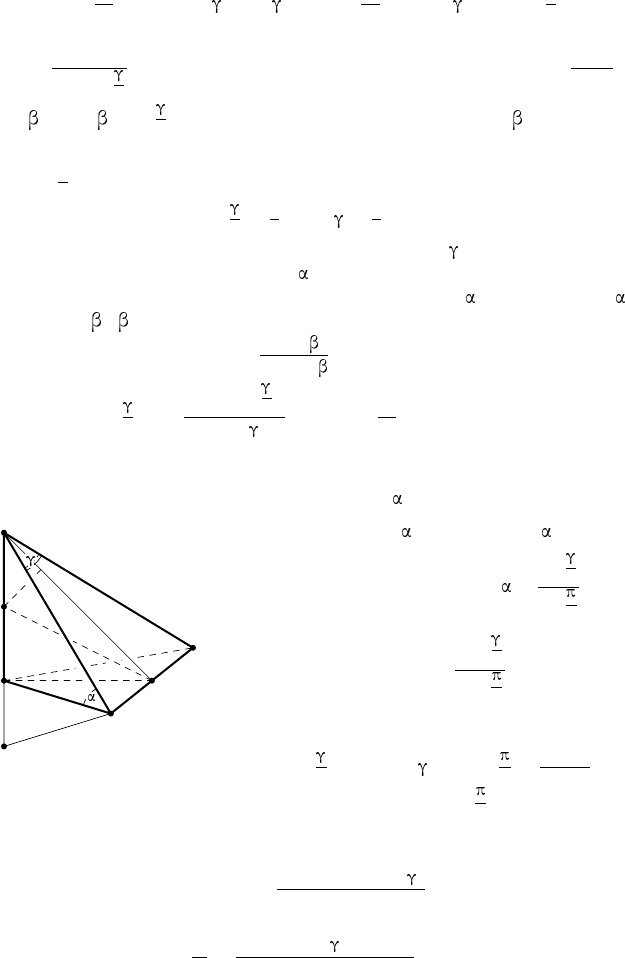
316. Р е ш е н и е. Применим способ введения вспомогательного угла.
Пусть N H — высота пирамиды, MN — диаметр описанной около неё
H
A
B
K
D
N
M
Рис. 61
сферы, ∠NAH = (рис. 61). Тогда
h = 2R sin
2
= 2R(1 − cos
2
).
Воспользуемся формулой cos =
sin
2
sin
n
и по-
лучим:
h = 2R
1 −
sin
2
2
sin
2
n
.
Выполним несложные преобразования:
2 sin
2
2
= 1 − cos , sin
2
n
=
k
2
1 + k
2
,
где k = tg
n
,
и выражение для h приведём к виду:
h = 2R
1 −
(1 + k
2
)(1 −cos )
2k
2
,
откуда
h
R
=
(1 + k
2
) cos + k
2
− 1
k
2
.
151
Для доказательства второго соотношения введём вспомогательные
отрезки. Пусть AB — сторона основания правильной пирамиды, N K —
апофема (см. рис. 61). Обозначим AB = 2a, N H = h, N K = l, HK = m.
Из прямоугольных треугольников AM N и AKN имеем: b
2
= 2Rh
и b
2
= a
2
+ l
2
. Откуда
R =
a
2
+ l
2
2h
.
Так как центр D сферы, вписанной в пирамиду, лежит на высоте
NH, и KD — биссектриса треугольника HKN, то
r
h −r
=
m
l
, откуда
r =
hm
l + m
. Таким образом, получаем:
r
R
=
2h
2
m
(l + m)(a
2
+ l
2
)
.
Из правой части полученного равенства исключим вспомогательные
неизвестные h и m. Так как h
2
= l
2
−m
2
и m =
a
tg
n
, то после несложных
преобразований получим:
r
R
=
2(k l − a)a
(a
2
+ l
2
)k
2
, где k = tg
n
.
Числитель и знаменатель выражения, стоящего в правой части равен-
ства, разделим на l
2
. Учитывая, что
a
l
= tg
2
, будем иметь:
r
R
=
2
“
k − tg
2
”
tg
2
“
1 + tg
2
2
”
k
2
.
А так как
2 tg
2
1 + tg
2
2
= sin и tg
2
=
1 −cos
sin
, то окончательно получим:
r
R
=
k sin + cos − 1
k
2
.
317. ctg
2
=
r
3k
2
; при k =
2
3
имеем = 90
◦
.
318.
n
6
(2R −h)h
2
sin
2
n
. У к а з а н и е. Объём пирамиды вычисляет-
ся по формуле V =
1
3
S
осн
· h, Если R
1
— радиус окружности, описанной
около основания, то S
осн
=
n
2
R
2
1
· sin
2
n
=
n
2
(2R − h)h sin
2
n
.
Объём пирамиды наибольший при h =
4
3
R (независимо от n). Наи-
большее значение V можно найти без использования производной, если
152
заметить, что сумма с омножителей произведения (4R − 2h) · h · h по-
стоянна и равна 4R, и поэтому произведение принимает наибольшее
значение при h = 4R − 2h.
319. cos =
3 ±
√
2
7
.
320. cos =
1 +
√
5 + k
2
4 + k
2
, где k = tg
n
, — величина двугранного угла
при основании пирамиды. У к а з а н и е. Будем пользоваться теми же
обозначениями, что и в задаче 316. Центры сфер симметричны относи-
тельно плоскости основания тогда и только тогда, когда h + r = R.
Получаем уравне ние (2 + k
2
) cos + k sin − 2 = 0. Вычислив tg
2
,
воспользуйтесь формулой cos =
1
k
tg
2
и установите, что
cos =
1 +
√
5 + k
2
4 + k
2
.
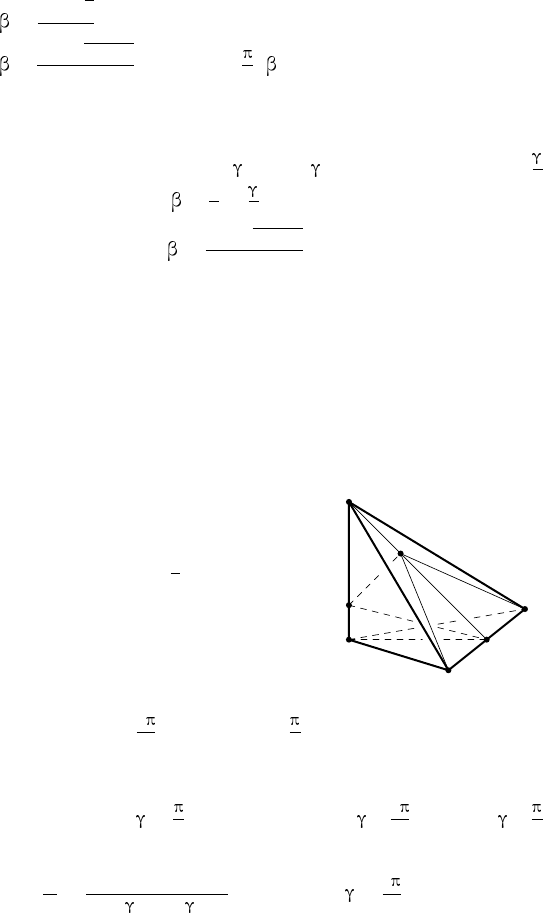
321. У к а з а н и е. Пусть N — вершина правильной пирамиды, J —
центр вписанной сферы и O — центр описанной сферы. Тогда
NJ = h − r, NO = R и d = JO = |N O − NJ| = |R + r − h|.
Затем воспользуйтесь формулами задачи 316.
322. Р е ш е н и е 1. Пусть NA
1
A
2
. . . A
n
— правильная n-угольная
пирамида, у которой центры вписанной и описанной сфер совпадают
(на рис. 62 изображена лишь часть пирамиды). Из общего их центра O
H
A
1
K
A
2
N
O
L
Рис. 62
проведём перпендикуляр OL к грани NA
1
A
2
.
Тогда A
1
L = A
2
L = N L, как проекции равных
наклонных OA
1
, OA
2
, ON. Значит, L — центр
окружности, описанной около треугольника
NA
1
A
2
, и поэтому ∠A
1
NA
2
=
1
2
∠A
1
LA
2
(впи-
санный угол вдвое меньше центрального,
опирающегося на ту же дугу). Поскольку O
в то же время и центр вписанной сферы, то
OH = OL. Теп ерь легко доказать, что A
1
L =
= A
1
H и 4A
1
LA
2
= 4A
1
HA
2
. Следователь-
но, ∠A
1
HA
2
= ∠A
1
LA
2
=
2
n
, а ∠A
1
NA
2
=
n
.
Верно и обратное предложение.
Р е ш е н и е 2. Из формулы задачи 321 следует, что d = 0 тогда
и только тогда, когда sin
−
n
= 0, при этом 0 < <
2
n
. Значит, =
n
.
323. Р е ш е н и е. Воспользуемся формулой з адачи 316:
R
r
=
k
2
k sin + cos − 1
, где 0 < <
2
n
.
153

Легко проверить истинность тождества
(k sin + cos )
2
+ (k cos − sin )
2
= 1 + k
2
,
откуда k sin + cos 6
√
1 + k
2
. Значит,
R
r
6
k
2
√
1 + k
2
− 1
= 1 +
√
1 + k
2
,
или
R
r
6 1 +
1
cos
n
, причём равенство достигается только тогда, когда
k cos = sin , или tg = tg
n
и, значит, =
n
.
Итак, равенство имеет место тогда и только тогда, когда центры
сфер совпадают (см. задачу 322).
324. а) Два ре шен ия: 45
◦
и arccos
2 −
√
2
2
. У к а з а н и е. Возможны
два случая: либо центр окружности, описанной около треугольника,
есть середина его основания, либо он лежит внутри треугольника. Обо-
значим угол при основании равнобедренного треугольника через , а ра-
диус описанной и вписанной окружностей соответственно чере з R и r.
В первом случае = 45
◦
и
R
r
= ctg 22,5
◦
= 1 +
√
2.
Во втором случае получаем систему уравнений:
r
R + r
= cos , 2r = −R cos 2 ,
откуда R
2
− 2Rr − r
2
= 0,
R
r
= 1 +
√
2 и cos =
2 −
√
2
2
.
Задачу можно решить проще, если воспользоваться теоремой Эйле-
ра d
2
= R
2
− 2Rr, где d — расстояние между центрами окружностей.
б) 30
◦
или 60
◦
, в том и другом случае
R
r
= 1 +
√
3.
325. Два решения: h = 1 +
√
5 и h = 3 +
√
5, в том и другом случае
d = 1 и центр описанной сферы лежит на вписанной сфере.
327. Р е ш е н и е. Пусть — угол наклона бокового ребра пирамиды
к плоскости её основани я, — угол наклона боковой грани пирамиды
к плоскости основания, h — высота пирамиды. Используя условие зада-
чи, составим систему уравнений:
tg =
1
cos
n
tg , h = 2R sin
2
,
r
R − r
= cos .
Первое уравнение почленно возведём в квадрат и получим:
1
cos
2
− 1 =
1
cos
2
n
1
cos
2
− 1
.
Из второго уравнения находим: cos
2
=
2R − h
2R
. Значения cos
2
и cos
2
подставим в предыдущее равенство и после несложных преобразований
154
получим квадратное уравнение относительно h:
h
2
− 2(R + r)h + 4Rr +
r
2
cos
2
n
= 0,
откуда h = R + r ±
s
(R − r)
2
−
r
2
cos
2
n
. Расстояние между центрами опи-
санной и вписанной сфер равно d = |h − R − r|. Следовательно,
d =
v
u
u
t
(R − r)
2
−
r
2
cos
2
n
, или d
2
= R
2
− 2Rr − r
2
tg
2
n
.
Из полученн ой формулы следует, что если d = r, т. е. центр опи-
санной сферы лежит на вписанной сфере, то
R
r
= 1 +
q
2 + tg
2
n
(зада-
ча 326). Кроме того, получаем неравен ство R − r >
r
cos
n
, или
R
r
> 1 +
1
cos
n
,
где равенство имеет мес то тогда и только тогда, когда центры сфер
совпадают.
328.
a(2b −a)
2
√
2b
2
− a
2
. 329. R
1
=
b
√
3
4
, R = b, h =
1
2
b.
330. r = 2, h = 8. У к а з а н и е. Воспользуйтесь формулой
R
1
= 2R cos
1 −
√
3
2
cos
(см. пример 3).
331.
a
“
1 −sin
2
”
2
√
2 cos − 1
, 0
◦
< < 60
◦
.
332. h = 6, d = 2 (d — расстояние между центрами сфер).
333. R
1
=
h cos
“
1 −sin
2
cos
”
sin
2
, 0 < <
2
. Р е ш е н и е. Пусть O
1
—
центр сферы, касающейся всех рёбер пирамиды, R
1
— её радиус. Вос-
пользуемся формулой R
1
= b ctg
1 − sin
2
cos
(см. пример 1) и со-
отношениями h = b sin , NO
1
=
R
1
cos
.
Получим:
R
1
=
h cos
“
1 −sin
n
cos
”
sin
2
, NO
1
=
h
“
1 −sin
n
cos
”
sin
2
, где 0 < <
2
.
155
Центр O
1
сферы лежит на продолжении высоты N H пирамиды, если
1 −sin
n
cos
sin
2
> 1,
или sin
n
< cos , откуда sin
n
< sin
2
−
и, значит, <
2
−
n
.
Если =
2
−
n
, то центр сферы совпадает с центром основания пи-
рамиды; если >
2
−
n
, то он лежи т на высоте пирамиды.
334.
h sin
2
“
1 −sin
2
”
sin
n
, 0 < <
2
n
.
335. R
1
= h cos
1 − sin
n
cos
, где h =
r (1 + cos )
cos
и cos =
1
r
1 + cos
2
n
tg
2
.
336. У к а з а н и е. Воспол ьзуйтесь формулой
R
1
= 2R cos
1 − sin
n
cos
.
R
R
1
=
√
2 только при = 45
◦
(центр сферы, касающейся всех рёбер пи-
рамиды, совпадает с центром описанной сферы).
338. У к а з а н и е. Центры сфер, описанной около правильной пи-
рамиды и касающейся всех её рёбер, лежит на высоте пирамиды или
её продолжении. Пусть N — вер ши на пирамиды. Тогда d = |N O −NO
1
|.
Докажите, что NO =
b
2 sin
, N O
1
=
2b −a
2 sin
, a = 2b sin
n
cos .
339. Центры сфер совпадают тогда и только тогда, когда n = 3, n = 4
или n = 5 и все рёбра пирамиды равны.
340. а)
a
˛
˛
˛
sin
n
− cos
˛
˛
˛
2 sin
n
sin
, б)
a|ctg 2 |
2 sin
n
.
341. cos =
sin
n
+
r
sin
2
n
+ 4
4
; если n = 6, то a ≈ 50
◦
. У к а з а н и е.
Воспользуйтесь результатом предыдущей задачи. Для вычисления уг-
ла составьте уравнение: 4 cos
2
− 2 sin
n
cos − 1 = 0.
342. arcc os
1
3
.
343. 4,5. У к а з а н и е. Докажите, что центр описанной сферы есть
середина ребра BD.
156
344.
a
2
p
2 + tg
2
;
(1 + sin )a
2
cos
.
345. 2
√
2 см. У к а з а н и е. Установите, что cos =
1
3
( — величина
угла при основании пирамиды).
346. Два решения: h
1
= 3 м и h
2
= 6 м. У к а з а н и е. Введите вспо-
могательные неизвестные: пусть a — длина стороны основания пирами-
ды и — величина двугранного угла при основании. Составьте систему
уравнений: V =
1
3
a
2
h, cos =
r
h −r
, a = 2r ctg
2
. Откуда 4r
2
h
2
− 3V h +
+ 6rV = 0.
При r = 1 м и V = 12 м
2
получим: h
1
= 3 м, h
2
= 6 м.
347.
1
4
c
3
sin 2 (sin + cos −1). 348.
2l
3
sin
2
cos
sin
. 349.
a
2
cos
4
2
.
350. R = 3.
352.
a
sin
;
a
2
p
1 − ctg
2
. Р е ш е н и е. Расстояние между двумя лю-
быми параллельными гранями параллелепипеда равно диаметру 2r впи-
санной сферы. Так как объём параллелепипеда равен произведению
площади грани на соответствующую высоту, равную 2r , то все грани
параллелепипеда имеют одинаковую площадь. Обозначив длину боко-
вого ребра через b, получим: ab sin = a
2
, откуда b =
a
sin
.
Пусть боковое ребро AA
1
параллелепипеда образует со сторонами
AB и AD основания углы, равные . Проведём высоту A
1
H паралле ле-
пипеда и высоту A
1
K боковой грани. Тогда точка H лежит на диагонали
основания, и легко наход им : A
1
K = a, HK = AK = a ctg . Из прямо-
угольного треугольника A
1
HK получим: 2r = A
1
H = a
p
1 − ctg
2
.
353. R = 5. 354.
√
34
3
≈ 1,9.
356.
√
97
8
≈ 3,5. У к а з а н и е. Центр сферы, проходящей через вер-
шины треугольника ABC, лежит на перпендикуляре m к плоскости
ABC, проходящем через центр описанной около н его окружности. Лег-
ко установить, что радиус этой окружности равен
9
√
2
4
.
Плоскость A
1
B
1
C
1
пересекает сферу по окружности, вписанной
в треугольник A
1
B
1
C
1
, точки касания которой со сторонами треуголь-
ника одинаково удалены от центра сферы, что возможно только тогда,
когда перпендикуляр m к плоскости ABC проходит через центр вписан-
ной в треугольник A
1
B
1
C
1
окружности. Радиус этой окружности легко
вычислить, он равен
√
2. Далее найдите высоту призмы и, пользуясь
теоремой Пифагора, вычислите радиус R сферы.
157
357. arccos
n −1
n + 1
; если n = 3, то = 60
◦
. 358. R = 5.
359. Два решени я: 7
√
2 и
√
2. 360. 1 : 5. 361. 1 : 3 : 9.
362. (
√
3 − 1) :
√
2 : 2. 363.
2
3
R. 364.
h(2 + tg )
2 tg
.
365.
4
3
. У к а з а н и е. Пусть R и r — радиусы шаров, — величина
двугранного угла при основании пирамиды. Установите, что cos =
=
R − r
R + r
, откуда
R
r
=
1 + cos
1 −cos
. Вычислите tg и cos .
366.
V
1
V
=
82 (2
√
3 −3)
243
. У к а з а н и е. Пусть R — радиус каждого из
трёх шаров с центрами O
1
, O
2
, O
3
и a — длина стороны основания.
Рассмотрите сечение приз мы плоскостью O
1
O
2
O
3
и установите, что
a = 2R(1 +
√
3).
Докажите, что радиус r четвёртого шара равен
R
3
, поэтому общий
объём всех четырёх шаров равен V
1
= 4 R
3
+
4
81
R
3
= 4 R
3
·
82
81
. Объём
же призмы V =
a
2
√
3
4
· 2R = 4R
3
√
3(2 +
√
3).
Отсюда
V
1
V
=
82 (2
√
3 −3)
243
≈ 0,49.
158
Обозначения и формулы
I. Тетраэдр
Длины рёбер тетраэдра ABCD обозначаются: AD = a, DB =b, DC =c,
BC = a
1
, CA = b
1
, AB = c
1
;
S
1
, S
2
, S
3
, S
4
— площади граней, противолежащих соответственно
вершинам A, B, C, D;
S
пол
— площадь полной поверхности тетраэдра;
h
1
, h
2
, h
3
, h
4
— высоты тетраэдра;
m
1
, m
2
, m
3
, m
4
— медианы тетраэдра, п роведё нн ые, соответственно,
из вершин A, B, C, D;
t
AB
, t
AC
, t
BC
— бимедианы тетраэдра, соединяющие середины рёбер
AB и CD, AC и BD, BC и DA;
V — объём тетраэдра; R — радиус описанной сферы;
r — радиус вписанной сферы; M — точка пересечения медиан;
O — центр описанной сферы; J — центр вписанной сферы.
Метрические соотношения
1. V =
abc
6
p
1 − cos
2
− cos
2
− cos
2
+ 2 cos cos cos ,
где = ∠BDC, = ∠CDA, = ∠ADB;
2. h
i
=
3V
S
i
, i = 1, 2, 3, 4;
3. m
2
4
=
a
2
+ b
2
+ c
2
3
−
a
2
1
+ b
2
1
+ c
2
1
9
;
4. t
2
AB
= (a
2
+ a
2
1
+ b
2
+ b
2
1
− c
2
− c
2
1
)/4;
5. r = 3V/S
пол
;
6. R =
T
6V
, где T — площадь треугольника, стороны которого числен-
но равны aa
1
, bb
1
, cc
1
.
II. Правильная пирамида
В правильной n-угольной пирамиде NA
1
A
2
. . . A
n
высота NH, N K —
апофема; A
1
A
2
= a, NA
1
= b, NH = h, NK = l (ри с. 36 и 37).
S
бок
— площадь боковой поверхности;
S — площадь полной поверхности;
R — радиус описанной сферы; r — радиус вписанной сферы;
R
1
— радиус окружности, описанной около основания.
159

Зависимости между элементами пирамиды
1. a = 2R
1
sin
n
; 2. b
2
= 2Rh; 3. R
2
1
= h(2R − h);
4. b = 2R sin ; 5. h = 2R sin
2
; 6. R
1
= R sin 2 ;
7. h = l sin ; 8. r =
h cos
1 + cos
; 9. S
бок
=
n
2
b
2
sin .
n-угольная
пирамида
n = 3 n = 4 n = 6
tg = cos
n
tg tg =
1
2
tg tg =
1
√
2
tg tg =
√
3
2
tg
cos =
1
sin
n
sin
2
cos =
2
√
3
sin
2
cos =
√
2 sin
2
cos = 2 sin
2
cos = ctg
n
tg
2
cos =
1
√
3
tg
2
cos = tg
2
cos =
√
3 tg
2
sin = ctg
n
ctg
2
sin =
1
√
3
ctg
2
sin = ctg
2
sin =
√
3 ctg
2
sin =
1
sin
n
cos
2
sin =
2
√
3
cos
2
sin =
√
2 cos
2
sin = 2 cos
2
III. Тела вращения
S
осн
— площадь основания; S
бок
— площадь боковой поверхности;
S — площадь полной поверхности; V — объём.
Цилиндр
R — радиус основания; h — высота цилиндра.
1. S
бок
= 2 Rh; 2. S = 2 R(R + h); 3. V = R
2
h.
Шар
R — радиус шара.
1. S = 4 R
2
; 2. V = 4 R
3
/3.
Конус
r — радиус основания конус а; h — высота; l — образующая.
1. S
бок
= Rl; 2. S = r(l + r); 3. V = r
2
h/3.
Усечённый конус
r
1
и r
2
— радиусы оснований усечённого конус а; h — высота;
l — образующая.
1. S
бок
= (r
1
+ r
2
)l; 2. S = (r
1
+ r
2
)l + r
2
1
+ r
2
2
;
3. V = h(r
2
1
+ r
1
r
2
+ r
2
2
)/3.
160
