Готман Э.Г. Стереометрические задачи и методы их решения
Подождите немного. Документ загружается.

Следовательно,
DP · AB =
1
2
(OA + OB + DC) · (OB − OA) =
=
1
2
( OB
2
− OA
2
+ DC · AB) =
1
2
DC · AB.
Но DC ·AB = 0, поэтому и DP ·AB = 0. Аналогично, DP ·BC = 0. Следо-
вательно, прямая DP перпендикулярна плоскости ABC. Точно так же
докажем, ч то прямые AP , BP и CP перпенд икулярны соответственно
плоскостям BCD, ACD и ABD. Значит, точка P есть точка пересечения
высот тетраэдра ABCD.
138. MN
2
=
1
4
(a
2
+ a
2
1
+ b
2
+ b
2
1
−c
2
−c
2
1
), где M и N — середины рёбер
AB и CD. У к а з а н и е. Воспользуйтесь равенством M N =
1
2
(AD + BC).
139. a) Р е ш е н и е. Воспользуемся результатом задачи 136:
OH = OA + OB + OC.
Сравнивая это равенство с равенством OM =
1
3
(OA + OB + OC), заклю-
чаем, что OH = 3OM.
140. a) Р е ш е н и е. Для центроида M треугольника ABC имеет
место равенство OM =
1
3
(OA + OB + OC).
Отсюда OM
2
=
1
9
(3R
2
+ 2OA ·OB + 2OA ·OC + 2OB ·OC). Так как
2OA ·OB = OA
2
+ OB
2
− AB
2
= 2R
2
− c
2
, то пол учим
OM
2
= R
2
−
1
9
(a
2
+ b
2
+ c
2
).
Отсюда следует, что для любого треугольника выполняется неравен-
ство a
2
+ b
2
+ c
2
6 9R
2
.
б) OM
2
= R
2
−
1
16
(a
2
+ b
2
+ c
2
+ a
2
1
+ b
2
1
+ c
2
1
).
С л е д с т в и е. Для всякого тетраэдра справедливо неравенство:
a
2
+ b
2
+ c
2
+ a
2
1
+ b
2
1
+ c
2
1
6 16R
2
.
141. a) Р е ш е н и е. Согласно правилу сложения векторов имеем:
P A = P M + M A, P B = P M + MB, P C = P M + M C. Возведём обе ча-
сти каждого равенства в квадрат. Затем воспользуемся соотношением
MA + MB + M C = 0 (см. задачу 112) и получим:
P A
2
+ P B
2
+ P C
2
= 3P M
2
+ AM
2
+ BM
2
+ CM
2
.
142. б) Центроид тетраэдра.
121
143. Р е ш е н и е. Имеем:
MA·MB =(OA −OM) ·(OB −OM)= OM
2
−(OA+ OB)·OM +OA·OB.
Пусть C — середина отрезка AB. Тогда OA + OB = 2OC. Откуда (так
как |OA| = |OB| = R) получим: OA · OB = 2OC
2
− R
2
. Таким образом,
MA·MB = OM
2
−2OC ·OM +2OC
2
−R
2
= OM
2
−R
2
−2OC ·(OM −OC).
Но OC ·(OM −OC) = OC · CM = 0, так как OC ⊥CM. Следовательно,
MA · MB = OM
2
− R
2
.
Аналогичный результат получится, есл и вместо сферы взять окруж-
ность.
Итак, произведение MA·M B зависит только от расстояний точки M
до центра сферы (окружности) и не зависит от выбора секущей, про-
ходящей через точку M. Число OM
2
− R
2
называют степенью точки
относительно данной сферы (окружности).
144. Р е ш е н и е. Данное равенство MA · M B = k можно записать
так: (OA − OM ) · (OB − OM ) = k, или OM
2
− (OA + OB) · OM + OA ·
·OB = k. Пусть O — середина отрезка AB и OA = R. Тогда OA + OB = 0
и OA ·OB = −R
2
. Таким образом, данное равенство приводится к виду:
OM
2
= k + R
2
.
Отсюда следует, что искомое множество точек представляет собой
сферу радиуса
√
k + R
2
с центром O, если число k + R
2
положитель-
но, точк у или пустое множество, если оно равно нулю или отрица-
тельно.
145. Перпенд ик уляр к плоскости треугольника ABC, проходящий
через ортоцентр этого треугольника.
146. Р е ш е н и е. Согласно условию задачи имеем:
(OA −OM )
2
+ (OB − OM)
2
= 2(OC − OM)
2
,
или
2OM · (OA + OB − 2OC) = OA
2
+ OB
2
− 2OC
2
.
Пусть O — центр окружности, описанной около треугольника ABC.
Тогда OA = OB = OC и OA + OB = 2OD, где D — середина отрезка AB.
Получаем:
OM · (OD − OC) = 0,
или
OM · CD = 0.
Отсюда следует, что искомое м ножество точек есть плоскость, прохо-
дящая через центр окружности, описанной около треугольни ка ABC
перпендикулярно медиане CD треугольника.
122
147. Р е ш е н и е. Имеем:
(OA −OM )
2
+ (OB − OM)
2
− (OC − OM)
2
= 0,
или
OM
2
+ 2(OC − OA − OB) · OM + OA
2
+ OB
2
− OC
2
= 0.
В качестве начальной точки O выберем сере дин у отрезка AB. Тогда
OA + OB = 0 и OA = OB. Предыдущее равенство принимает вид:
OM
2
+ 2OC · OM = OC
2
− 2OA
2
,
или
(OM + OC)
2
= 2(OC
2
− OA
2
).
Пусть D — точка, симметричная точке C относительно точки O, т. е.
D — вершина параллелограмма ABCD. В таком случае OD = −OC,
OM + OC = OM − OD = DM , и равенство принимает простой вид:
DM
2
= 2(OC
2
− OA
2
).
Итак, если OC > OA, то искомое множество есть сфера радиуса
p
2(OC
2
− OA
2
); если O C = OA, то искомое множество — одна точка D,
при этом ∠ACB = 90
◦
; если OC < OA, то искомое множество точек —
пустое.
148. Р е ш е н и е. Если CM — медиана треугольника, то
CM =
1
2
(CA + CB).
Так как векторы CA и CB не коллинеарны, то
CM =
1
2
|CA + CB| <
1
2
(CA + CB).
Задача для тетраэдра решается аналогично.
Если DM — медиана тетраэдра, то
DM =
1
3
(DA + DB + DC).
Векторы DA, DB, DC не коллинеарны, следовательно,
DM <
1
3
(DA + DB + DC).
Значит, медиана тетраэдра меньше
1
3
суммы трёх рёбер, исходящих из
той же вершины.
149. У к а з а н и е. Установите, что (DA + DB + DC)
2
> 0, и восполь-
зуйтесь теоремой косинусов 2DA · DB = DA
2
+ DB
2
− AB
2
.
150. Р е ш е н и е. Вектор s = AB + AD −AC равен нулевому векто-
ру тогда и только тогда, когда ABCD — параллелогр амм , в противном
123
случае s
2
> 0. Итак, имеем:
AB
2
+ AD
2
+ AC
2
+ 2AB · AD − 2AB · AC − 2AD · AC > 0.
Применив теорему косинусов, получим:
AB
2
+ BC
2
+ CD
2
+ DA
2
− AC
2
− BD
2
> 0,
где равенство достигается только для параллелограм ма (включая вы-
рожденный случай).
151. cos = 1 −
3
2
cos
2
; если tg =
√
2, то = 60
◦
.
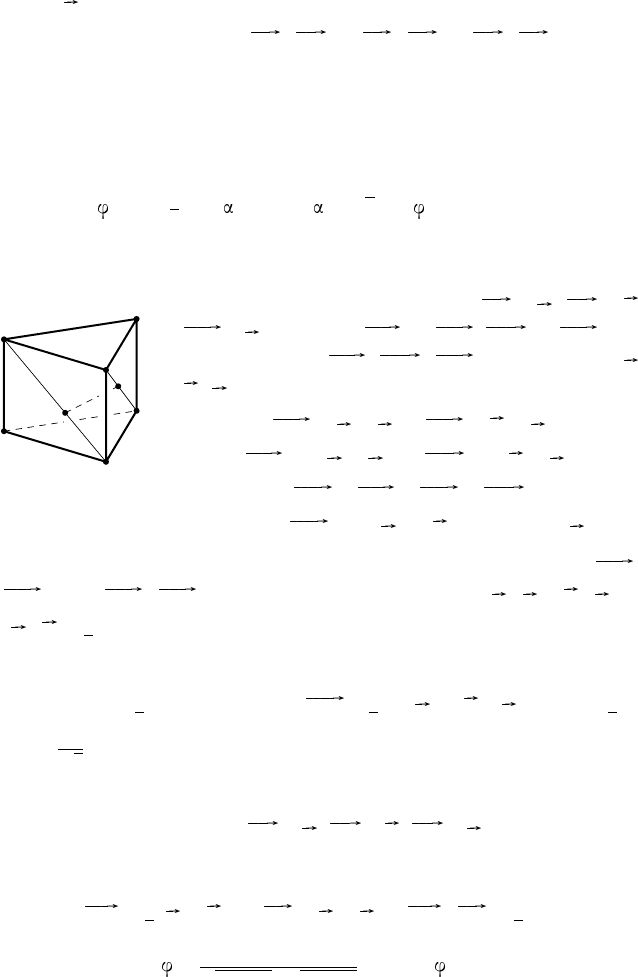
152. Р е ш е н и е. Рассмотрим правильную треугольную призму
ABCA
1
B
1
C
1
(рис. 51). Требуется построить общий перпендикуляр M N
A
B
C
A
1
B
1
C
1
M
N
Рис. 51
прямых BA
1
и CB
1
.
Выберем базисные векторы: BA = a , BC = b ,
BB
1
= c . Положим BM = xBA
1
, B
1
N = yB
1
C. Вы-
разим векторы BM , B
1
N, MN через векторы a ,
b , c . Получим:
BA
1
= a + c , B
1
C = b − c ,
BM = x( a + c ), B
1
N = y( b − c ),
MN = MB + BB
1
+ B
1
N,
или MN = −x a + y b + (1 − x − y) c .
Так как MN — общий перпендикуляр прямых BA
1
и CB
1
, то MN ·
· BA
1
= 0 и MN · B
1
C = 0. Согласно условию задачи a · c = b · c = 0
и a · b =
1
2
a
2
. Получаем систему уравнений:
x + 4y − 2 = 0, 4x + y − 2 = 0.
Отсюда x = y =
2
5
. Следовательно, MN =
1
5
(−2 a + 2 b + c ), M N
2
=
1
5
a
2
,
MN =
1
√
5
a.
Найденные значения x и y дают возможность построить общий пер-
пендикуляр прямых BA
1
и CB
1
.
153. Р е ш е н и е. Пусть DA = a , DB = b , DC = c . Длины этих век-
торов обозначим соответственно через a, b, c.
Имеем:
DK =
1
2
( a + b ), CA = a − c , DK · CA =
1
2
a
2
,
cos =
a
2
√
a
2
+ b
2
·
√
a
2
+ c
2
, 0
◦
< < 90
◦
.
124
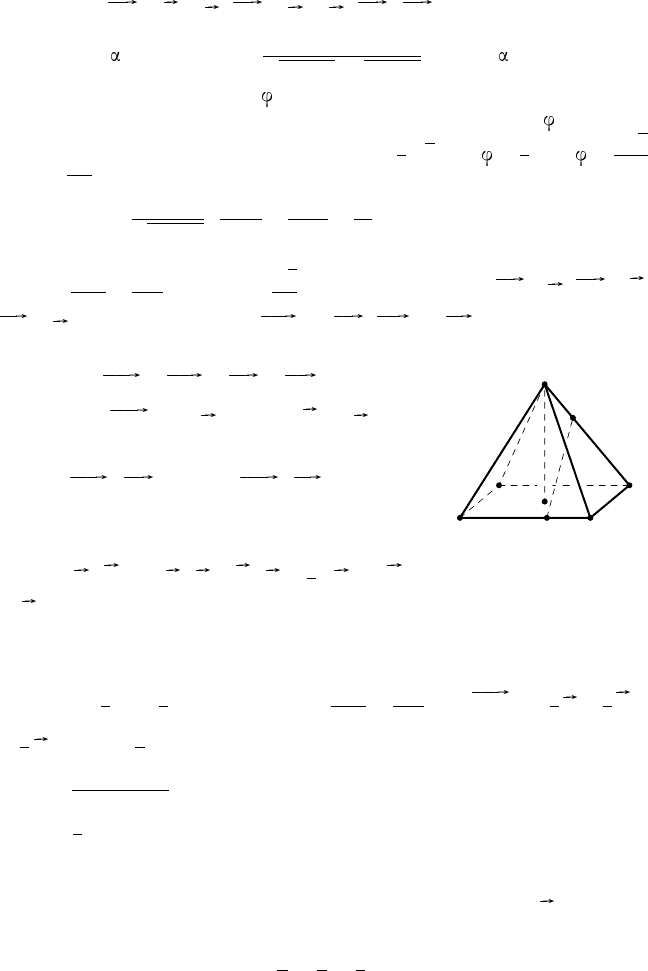
Так как AB = b − a , AC = c − a , AB · AC = a
2
, то
cos = cos ∠BAC =
a
2
√
a
2
+ b
2
·
√
a
2
+ c
2
, 0
◦
< < 90
◦
.
Следовательно, ∠BAC = .
Расстояние от точки K до прямой AC равно d = AK sin .
Если DA = 1, DB = DC = 2, то AK =
1
2
√
5, cos =
1
5
, sin =
2
√
6
5
и d =
√
1,2 ≈ 1,1.
154. MN =
ab
√
a
2
+ b
2
,
AM
MA
1
=
BN
ND
1
=
a
2
b
2
, MN — общий перпендикуляр
прямых AA
1
и BD
1
.
155.
AM
MB
=
CN
NS
= 2, M N =
√
6
3
. Р е ш е н и е. Пусть BA = a , BC = b ,
BS = c (рис. 52). Положим BM = xBA, CN = yCS. Согласно правилу
A
B
C
D
M
N
S
Рис. 52
сложения векторов
MN = MB + BC + CN,
или MN = −x a + (1 − y) b + y c .
Из условия задачи следует, что
MN · BA = 0 и M N · CS = 0.
Так как длины всех рёбер пирамиды рав-
ны 1, то ∠ABC = 90
◦
, ∠ABS = ∠CBS = 60
◦
.
Значит, a · b = 0, a · c = b · c =
1
2
. a
2
= b
2
=
= c
2
= 1. Подставив найденные значения в предыдущие равенства, по-
лучаем систему уравнений:
2x − y = 0, x − 2y + 1 = 0,
откуда x =
1
3
, y =
2
3
. Далее находим:
AM
MB
=
CN
NS
= 2, M N = −
1
3
a +
1
3
b +
+
2
3
c , M N
2
=
2
3
.
156.
abc
ab + bc + ca
.
157.
7
6
. У к а з а н и е. Точку C примите за начало координат, а на-
правленные прямые CA, CB и CC
1
— за оси координат. Ве рши ны приз-
мы будут иметь координаты: A(2, 0, 0), B(0, 3, 0), C
1
(0, 0, 1).
Уравнение плоскости ABC
1
: 3x + 2y + 6z −6 = 0. Вектор n = {3, 2, 6}
является направляющим вектором прямой CM, уравнение которой
x
3
=
y
2
=
z
6
.
125
Запишите уравнение плоскости A
1
B
1
C
1
и решите систему получен-
ных уравнений. Точка M имеет координаты
1
2
, 13, 1
.
158.
r
2
3
. Р е ш е н и е. Введём в пространстве прямоугольную систе-
му координат с началом в центре O квадрата ABCD. Осям координат
придадим направления векторов OA, OB и ON. Так как ∠NAO = 45
◦
,
то OA = ON и вершины пирамиды будут иметь координаты: A(1, 0, 0),
B(0, 1, 0), N (0, 0, 1), D(0, −1, 0). Запишем уравнение плоскости ABN :
x + y + z = 1. Вектор n = {1, 1, 1} перпендикулярен плоскости ABN .
Вектор DN имеет координаты {0, 1, 1}. Обозначив искомый угол че-
рез , а угол между век торами DN и n — ч ере з . Легко доказать, что
sin = |cos |, следовательно
sin =
|DN · n |
|DN | · |n |
.
Координаты векторов DN и n найдены, значит,
sin =
2
√
2 ·
√
3
=
r
2
3
.
159.
3
32
(куб. ед.). У к а з а н и е. Введите прямоугольную систему
координат с началом в центре O треугольника ABC, а осям координат
придайте направление векторов OA, BC и OS. Тогда вершины пирами-
ды будут иметь координаты: A(1, 0, 0), B
−
1
2
, −
3
2
, 0
, S(0, 0,
√
3).
160. MN = 1,5; arcsin
√
6
9
. 161. BL = 6, S
сеч
= 6 (кв. ед.), arccos
2
9
.
162. 3
√
17 (кв. ед .).
163. S
сеч
=
√
6
4
a
2
,
D M
MB
1
=
1
5
. У к а з а н и е. Введите в пространстве
прямоугольную систему координат с началом в точке D так, чтобы
вершины призмы имели координаты A(a, 0, 0), C(0, a, 0), D
1
(0, 0, 2a).
Запишите уравнение плоскости сеч ени я: x + y + 2z = a. Докажите, что
эта плоскость пересекает ребро DD
1
в такой точке E, что DE =
1
2
a.
164. 3
√
3a.
166.
1
3
. У к а з а н и е. Пусть NABCD — данная пирамида. Все дву-
гранные углы при основании пирамиды равны, значит, центр сферы,
вписанной в пирамиду, л ежи т на её высоте. Основание высоты NO
пирамиды есть точка пересечения диагоналей ромба ABCD. Введите
126

прямоугольную систему координат с осями OA, OB и ON. Пусть r —
радиус вписанной сферы, тогда её це нтр имеет координаты (0, 0, r).
Для вычисления r составьте уравнение, учитывая, что расстояние от
центра сферы до плоскости ABN равно r.
167. 3.
168. а) m + n ±
√
2mn, задача имеет два решения.
б) 2r = m + n + p ±
√
2mn + 2mp + 2np − m
2
− n
2
− p
2
, где r — радиус
сферы. 1) Два решения: r
1
= 3 и r
2
= 5. 2) Одно решение: r = 3. 3) Ре-
шений нет.
169. Р е ш е н и е. Выберем вершину O — тетраэдра OABC за нача-
ло прямоугольной системы координат, а оси выберем так, чтобы дру-
гие вершины имели координаты: A(a, 0, 0), B(0, b, 0), C(0, 0, c). Введём
ещё обозначения: P (x, y, z), OP = p, AP = a, BP = b, CP = c
1
. По фор-
муле расстояния между двумя точками находим:
a
2
1
= (x − a)
2
+ y
2
+ z
2
, p
2
= x
2
+ y
2
+ z
2
.
Отсюда a
2
1
= a
2
1 −
2x
a
+ p
2
. Аналогично, b
2
1
= b
2
1 −
2y
c
+ p
2
, c
2
1
=
= c
2
1 −
2z
c
+ p
2
. Следовательно,
a
2
1
a
2
+
b
2
1
b
2
+
c
2
1
c
2
= 3 − 2
x
a
+
y
b
+
z
c
+
+ p
2
1
a
2
+
1
b
2
+
1
c
2
. Точка P принадлежит плоскости ABC, поэтому
x
a
+
y
b
+
z
c
= 1. Далее,
1
a
2
+
1
b
2
+
1
c
2
=
1
h
2
(см. пример 1). А так как
a
1
a
= u,
b
1
b
= v,
c
1
c
= w и
p
2
h
2
=
1
sin
2
= 1 + ctg
2
, то полученное выше р авенс тво
принимает вид:
u
2
+ v
2
+ w
2
= 2 + ctg
2
.
170.
4
3
171.
√
14
4
a.
172.
√
22
4
a. У к а з а н и е. Ведите прямоугольную систему координат
с началом в точке A так, чтобы вершины B, D, A
1
призмы имели ко-
ординаты: B(a, 0, 0), D(0, a, 0), A
1
(0, 0,
√
2a). Пусть O(x, y, z) — центр
сферы. Докажите, что x =
a
2
, y = a, z =
√
2
4
a.
173. 1,
SN
NB
=
2
3
. У к а з а н и е. Прямоугольную систему координат
можно выбрать так, чтобы вершины пирамиды имели координаты:
C(0, 0, 0), B(0, 1, 0), A
√
3
2
,
1
2
, 0
, S(0, 0, 3), M
√
3
4
,
1
4
,
√
3
2
. Ис-
пользуя условие OB = OM, найдите z.
174. 8a
2
. 175. Сфера, описанн ая около куба.
127
176. Сфера. Центр сферы — середина отрезка AB, радиус равен
√
3
2
a,
где a = AB.
177. а) Сфера, центр которой лежит на луче AB на расстоянии
4
3
b,
где b = AB. Радиус сферы равен
2
3
b. У к а з а н и е. Точку A примите
за н ачало прямоугольной системы координат. Ось Oy проведём через
точку B. Полагая B(0, b, 0) и M (x, y, z), получите уравнение:
3x
2
+ 3y
2
+ 3z
2
− 8by + 4b
2
= 0,
или
x
2
+
y −
4
3
b
2
+ z
2
=
4
9
b
2
.
Полезно сначала решить задачу для точек плоскости.
б) Сфера, если k > 1. Плоскость, перпендикулярная отрезку AB
и проходящая через середину отрезка.
178. Сфера, уравнение которой (x + a)
2
+ (y + b)
2
+ z
2
= 2(a
2
+ b
2
), где
a = CA, b = CB, точка C — начало координ ат.
179. а) Окружность, проходящая через вершины A и B (без точек A
и B), центр которой симметричен вершине C треугольника относитель-
но прямой AB.
б) Сфера, проходящая через вершины A и B треугольника с цен-
тром, симметричным вершин е C относительно прямой AB. Р е ш е н и е.
Выберем прямоугольную систему координат с началом O в середине от-
резка AB, а за оси Ox и Oy примем направленные прямые OC и OB.
Полагая AB = 2, вершинам треугольника ABC можно придать коорди-
наты: A(0, −1, 0), B(0, 1, 0), C(
√
3, 0, 0). Пусть M(x, y, z) — произволь-
ная точка пространства. По формуле расстояния между двумя точками
имеем:
MA
2
= x
2
+ (y + 1)
2
+ z
2
,
MB
2
= x
2
+ (y − 1)
2
+ z
2
,
MC
2
= (x −
√
3)
2
+ y
2
+ z
2
.
Подставив в равенство MA
2
+ MB
2
= MC
2
эти значения, получим
уравнение:
x
2
+ y
2
+ z
2
+ 2
√
3x − 1 = 0,
или
(x +
√
3)
2
+ y
2
+ z
2
= 4.
Итак, искомое множество точек есть сфера радиуса R = 2 с центром
в точке D(−
√
3, 0, 0).
180. Сфера, описанн ая около тетраэдра.
181. Куб. У к а з а н и е. Воспол ьзуйтесь неравенством x
2
+ y
2
+ z
2
6
6 xy + yz + zx.
128

182. а)
√
3d
2
. б) Параллелепипед, основанием которого служит квад-
рат, а боковое ребро равно диагонали основания. У к а з а н и е. Пусть
ABCDA
1
B
1
C
1
D
1
— данный параллелепипед, AC
1
= d. Введите перемен-
ные: ∠CAC
1
= и ∠CAB = . Установите, что площадь боковой поверх-
ности есть функция
S
бок
= d
2
sin 2 (sin + cos ),
которая при = 45
◦
и = 45
◦
принимает наибольшее значение.
183. Дно бассейна должно иметь форму квадрата, высота же — вдвое
меньше стороны квадрата. Р е ш е н и е. Обозначим через x и y — линей-
ные размеры дна и через z — глубину бассейна. Тогда объём бассейна
V = xyz, а площадь дна и стен S = xy + 2xz + 2yz. Применив неравен-
ство между средним арифметическим и средним геометрическим трёх
положительных чисел, получим:
S 6 3
3
p
4x
2
y
2
z
2
= 3
3
√
4V
2
.
Равенство имеет место только при xy = 2xz = 2yz, т. е. когда x = y =
= 2z =
3
√
2V .
184. а) Высота прямоугольника вдвое меньше высоты треугольни ка.
б) Высота цилиндра должна составлять половину высоты конуса.
185. Высота цилиндра наибольшего объёма равна
1
3
высоты конуса.
186. У к а з а н и е. Обозначьте через a и h соответственно сторону
основания и высоту пирамиды, через V — объём вписанного параллеле-
пипеда, через x — его высоту. Установите, что
V =
a
2
h
2
(h − x)
2
x, где 0 < x < h.
Полученную формулу представьте в виде:
V =
a
2
2h
2
2x(h − x)(h − x).
Поскольку сумма трёх последних сомножителей постоянна и равна 2h,
то V
max
=
4
27
a
2
h при x =
1
3
h.
187. а) Цилиндр с квадратным осевым сечением. б)
√
5 −1. 188.
4
3
R.
189. V
max
=
8
3
R
3
при h = 4R. Р е ш е н и е. Обозначим через h и r
высоту конуса и радиус его основания соответственно. Выразим объём
конуса по формуле
V =
1
3
r
2
h.
В качестве независимого переменного возьмём угол наклона образу-
ющей конуса к п лоскости основани я. Обозначим его через 2x. Тогда
имеем: r = R ctg x, h = R ctg x tg 2x, и V =
1
3
R
3
ctg
3
x tg 2x.
129
Требуется найти наименьшее значение функции
f(x) = ctg
3
x tg 2x, где 0
◦
< x < 45
◦
.
Воспользуемся формулой tg 2x =
2 tg x
1 −tg
2
x
и, выполнив несложные пре-
образования, получим:
f(x) =
2
tg
2
x(1 −tg
2
x)
.
Знаменатель дроби имеет наибольшее значение, а функц ия f(x) —
наименьшее, когда tg
2
x = 1 − tg
2
x, т. е. tg x =
1
√
2
. При этом r = R
√
2
и h = 4R. Наименьшее значение объёма конуса равно
8
3
R
3
, объём шара
V
1
=
4
3
R
3
, следовательно, V > 2V
1
.
191.
1
6
a. Р е ш е н и е. Обозначим сторону вырезаемого квадрата че-
рез x, тогда сторона квадратного дна коробки равна a − 2x, высота
коробки равна x. Следовательно, объём коробки равен
V = (a − 2x)
2
x =
1
4
(a − 2x)(a − 2x) · 4x.
Так как сумма (a −2x) + (a −2x) + 4x = 2a постоянна, то объём прини-
мает наибольшее значение при 4x = a − 2x, откуда x =
1
6
a.
192. V
max
=
4
√
3
27
l
3
, при этом высота пир амид ы вдвое меньше стороны
основания.
193. V
max
=
2 l
3
9
√
3
при = arcctg
√
2.
194. V =
1
12
x
2
√
4 − 2x
2
, 0 < x <
√
2, V
max
=
2
√
3
27
при x =
2
√
3
.
195. V =
1
6
x
√
3 − x
2
, 0 < x <
√
3, V
max
=
1
4
при x =
r
3
2
. У к а з а н и е.
Пусть NABCD — четырёхугольная пирамида, NA = x и каждое из
остальных семи рёбер имеет длину, равную 1. Основанием пирами-
ды служит ромб ABCD, диагонали которого пересекаются в точке O.
Докажите, что AO = OC = ON и ∠AN C = 90
◦
.
Плоскость ANC является плоскостью симметрии пирамиды NABCD,
поэтому её объём можно найти по формуле V =
1
3
S
AN C
· BD.
196. S
min
=
√
6
2
a
2
при = arccos
√
6
3
.
Р е ш е н и е 1. Пусть плоскость, проходящая через диагональ BD
1
куба, пересекает его ре бро AA
1
в точке K (рис. 53). Тогда она пере-
130
