Гонтарь И.Н., Волчихина Н.И. Сопротивление материалов
Подождите немного. Документ загружается.

51
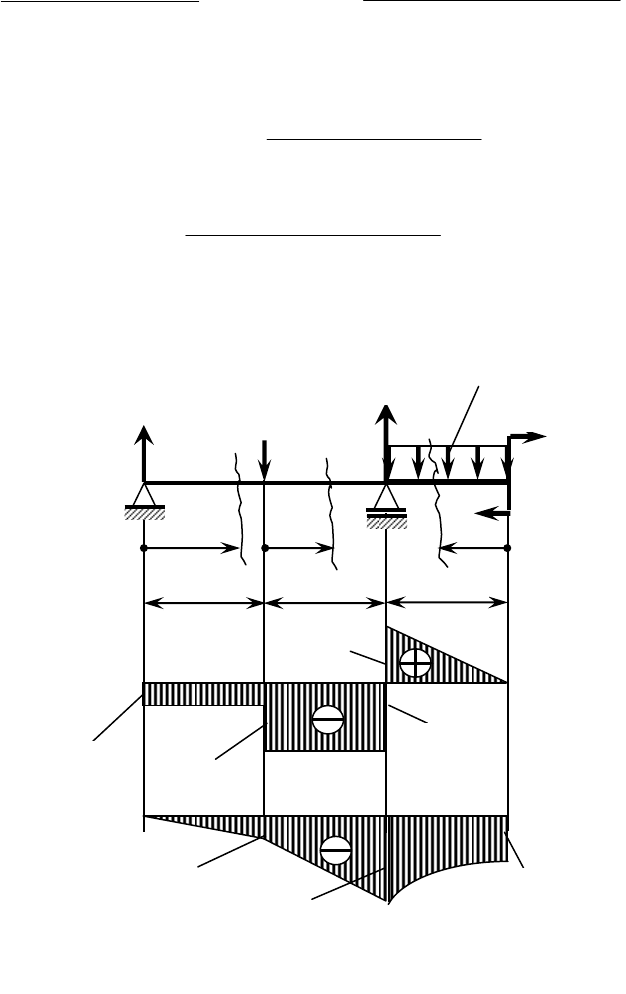
Рисунок 6.1
М
х
в)
10 кН
⋅
м
2,5 кН⋅м
15 кН
⋅
м
10 кН
0
б)
12,5 кН
12,5 кН
2,5 кН
Q
y
z
R
A
I
а)
BА
а = 1 м
а = 1 м
а = 1 м
Р = 10 кН
m = 10 кН⋅м
q = 10 кН/м
R
В
II III
z
z
a
maqaP
R
B
2
2,5
2
++
=
,
.êÍ5,22
2
1015,210110
2
=
+⋅⋅+⋅
=
B
R
Σ
m
В
= 0; R
А
2а − Р а + (q а) (0,5 а) + m = 0.
a
maqaP
R
2
À
2
0,5 −−
= ;
êÍ.2,5
2
1010,510110
2
−=
−⋅⋅−⋅
=
À
R
Знак «−» показывает, что направление реакции А нужно поме-
нять на обратное.
Проверка:
Σ Y = 0;
−
R
A
−
Р + R
B
−
q а = 0;
−2,5 − 10 + 22,5 − 10⋅1 = 0;
0 ≡ 0.

52
Выделим на балке три участка (I, II, III), где поперечная сила
y
Q и изгибающий момент
x
M изменяются по одному и тому же за-
кону (см. рисунок 6.1,а).
Внутренние силы
y
Q
и
x
M определяем методом сечений, про-
водя произвольные поперечные сечения на каждом участке.
Эти сечения проводим на расстоянии z от начала или конца
каждого участка.
Составим уравнения
y
Q и
x
M
для произвольных сечений каж-
дого участка.
I участок (0 ≤ z ≤ a = 1 м):
I
y
Q = −R
A
= −2,5 кН;
I
x
M = −R
A
z = −2,5z.
Из этих уравнений видно, что
I
y
Q − величина, постоянная на
всём участке, а
I
x
M изменяется по линейному закону.
Проанализируем
I
x
M :
при z = 0
I
x
M = 0;
при z = 1 м
I
x
M = −2,5 ⋅ 1 = −2,5 кН⋅м.
Аналогично определяем
y
Q и
x
M на остальных участках.
II участок (0 ≤ z ≤ a = 1 м):
II
y
Q = −R
A
− Р = −2,5 − 10 = −12,5 кН (постоянная величина).
II
x
M = −R
A
(а + z) − P z = − 2,5(1 + z) −10 z (линейный закон),
при z = 0
II
x
M = −2,5 (1 + 0) − 10 ⋅ 0 = −2,5 кН⋅м;
при z = 1 м
II
x
M = −2,5 (1 + 1) − 10 ⋅ 1 = −15 кН⋅м.
III участок (0 ≤ z ≤ a = 1 м):
III
y
Q = q z = 10⋅z (линейный закон),
при z = 0
III
y
Q
= 0;
при z = 1 м
III
y
Q = 10 ⋅ 1 = 10 кН.
III
x
M = −m − q z (
2
z
).
III
x
M = −m −
2
2
z
q
(квадратное уравнение – парабола);
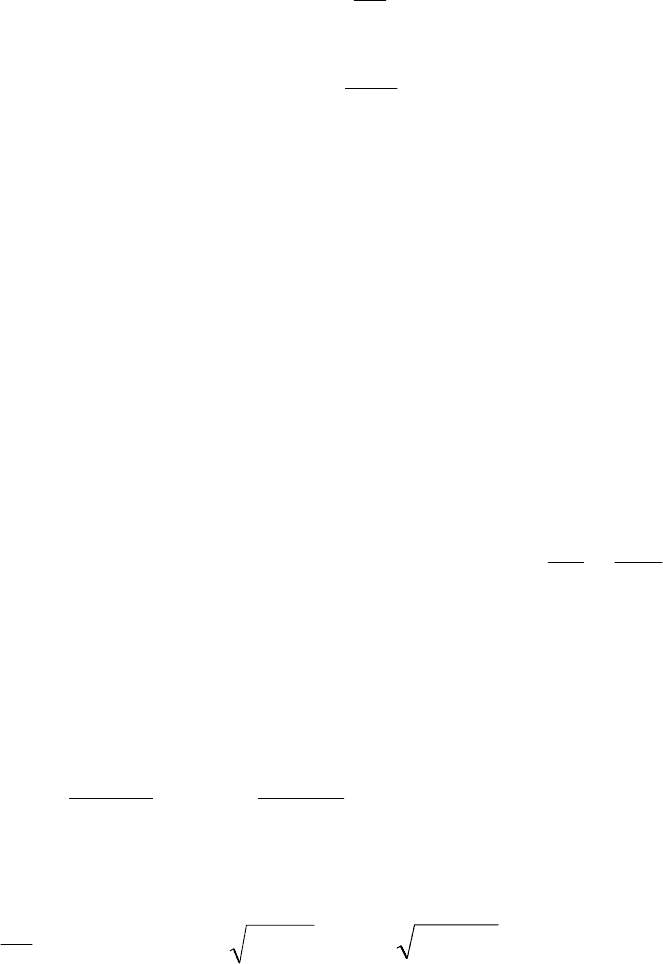
53
при z = 0
III
x
M = −10 −
2
0
10
2
= −10 кН⋅м;
при z = 1 м
III
x
M = −10 −
2
1,0
2
q = −15 кН⋅м.
По полученным данным построим эпюру
y
Q и эпюру
x
M
, от-
кладываем положительные значения выше нулевой линии, а отрица-
тельные значения – ниже нулевой линии: эпюра
y
Q – на рисун-
ке 6.1,б, эпюра
x
M
– на рисунке 6.1,в.
б)
Подбор размеров поперечного сечения.
Из условия прочности по нормальным напряжениям подобрать
размер квадратного сечения балки (см. рисунок 6.1) при следующих
данных:
материал – сталь 15; σ
т
= 240 МПа; n
т
= 1,5.
Определяем
допускаемое напряжение 160
5,1
240
][
ò
ò
==
σ
=σ
n
МПа.
По эпюре
x
M определяем
x
Mmax – сечение В:
x
Mmax = 15 кН⋅м = 15 ⋅ 10
6
Н⋅мм.
Определяем из условия прочности
x
W по формуле (6.1):
.;
[
335
6
max
ñì 93,8ìì10 0,938
160
1015
]
=⋅=
⋅
=
σ
=
x
x
x
W
M
W
Для квадратного сечения (размер поперечного сечения b)
6
3
b
W
x
= , отсюда см8,2593,866
3
3
; =⋅=⋅= bWb
x
; b = 8,25 см.
6.2 Дифференциальные
зависимости Журавского и проверка
правильности построения эпюр
Пояснения к решению задач 11 и 12 (см. приложение А)
Изгибающий момент
x
M , поперечная сила
y
Q и интенсив-
ность распределённой нагрузки q связаны между собой следующими
дифференциальными зависимостями Журавского:

54
⎪
⎪
⎭
⎪
⎪
⎬
⎫
==
=
2
2
;
dz
Md
dz
dQ
q
dz
dM
Q
x
y
x
y
. (6.2)
Таким образом:
−
первая производная от изгибающего момента по абсциссе
поперечного сечения балки равна поперечной силе;
−
первая производная от поперечной силы (или вторая произ-
водная от изгибающего момента) по абсциссе поперечного сечения
балки равна интенсивности распределённой нагрузки.
Из (6.2) вытекают следующие интегральные зависимости:
,
00
00
; QqQMdzQM dz
z
z
z
z
yyx
+=+=
∫∫
(6.3)
где
0
M − изгибающий момент в начале участка;
0
Q − поперечная сила в начале участка.
Из приведённых зависимостей (6.2) и (6.3) можно сделать сле-
дующие выводы.
Пункт 1. На участке, где отсутствует распределённая нагрузка,
эпюра
ó
Q имеет вид горизонтальной прямой, а эпюра
x
M имеет вид
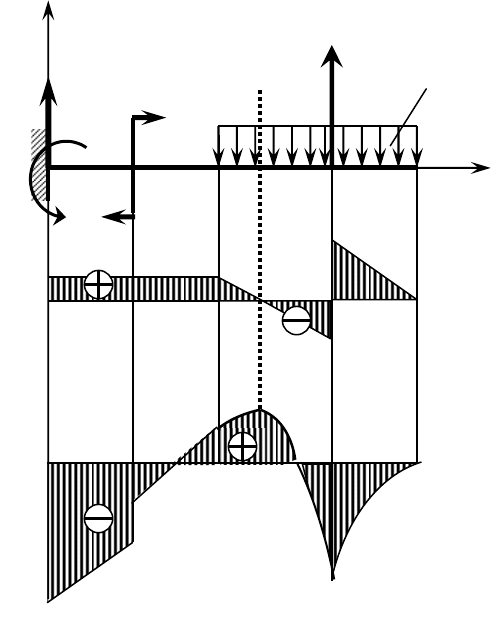
наклонной прямой (рисунок 6.2, участки а
−
б,б
−
в).
Пункт 2. На участке, где имеется равномерно распределённая
нагрузка q, эпюра
ó
Q имеет вид наклонной прямой, а эпюра
x
M из-
меняется по квадратичной параболе (рисунок 6.2, участки в
−
г, г
−
д).
Пункт 3. На участке балки (идём слева направо):
− если
ó
Q
положительна, то
x
M возрастает (участки а
−
б, б
−
в,
в
−
с, г
−
д);
− если
ó
Q отрицательна, то
x
M
убывает (участок с
−
г);
− если
ó
Q = 0, то
x
M
= const (чистый изгиб).
Если идём справа налево – всё наоборот.
Пункт 4. На участке, где эпюра
ó
Q пересекает ось Z,
x
M дос-
тигает экстремального значения (сечения с и г).
Если эпюра
ó
Q меняет знак с плюса на минус (когда идём слева
направо), то момент
x
M
имеет положительный экстремум (сечение с).
55
Рисунок 6.2
Если эпюра
ó
Q меняет знак с минуса на плюс, то
x
M имеет
отрицательный экстремум (сечение с).
Пункт 5. Поперечная сила в любом сечении численно равна
площади эпюры распределённой нагрузки от начала участка до рас-
сматриваемого сечения, сложенной с поперечной силой в начале
участка (с учётом знаков, если распределенная нагрузка направлена
вниз – знак минус, и наоборот).
Изгибающий момент в любом сечении численно равен площа-
ди эпюры поперечной силы от
начала участка до рассматриваемого
сечения (с учетом знаков), сложенный с изгибающим моментом в
начале участка.
При рассмотрении правой части балки площади эпюр
ó
Q и
x
M надо брать с обратным знаком.
Пункт 6. На криволинейном участке эпюры
x
M её выпуклость
направлена в сторону, противоположную направлению распреде-
лённой нагрузки (участки в
−
с, с
−
г, г
−
д).
Пункт 7. В сечении, где к балке приложена сосредоточенная
сила Р, на эпюре
y
Q происходит скачкообразное изменение ордина-
ты («скачок») на величину приложенной силы (сечения а и г).
Q
y
R
А
m
Z
А
Р
q
Y
a
c
б
в
г
д
M
x
56
На эпюре
x
M в этом месте происходит излом эпюры, т.е. смежные
участки эпюры не имеют плавного сопряжения (сечения а и г).
Пункт 8. В сечении, где к балке приложен сосредоточенный
момент сил m, на эпюре
x
M происходит «скачок» ординат на вели-
чину приложенного момента (сечение б).
Эти пункты выводов используются для проверки правильности
построения эпюр
ó
Q и
x
M в характерных сечениях балки без со-
ставления уравнений
ó
Q
и
x
M для отдельных её участков.
Пример решения задачи 11
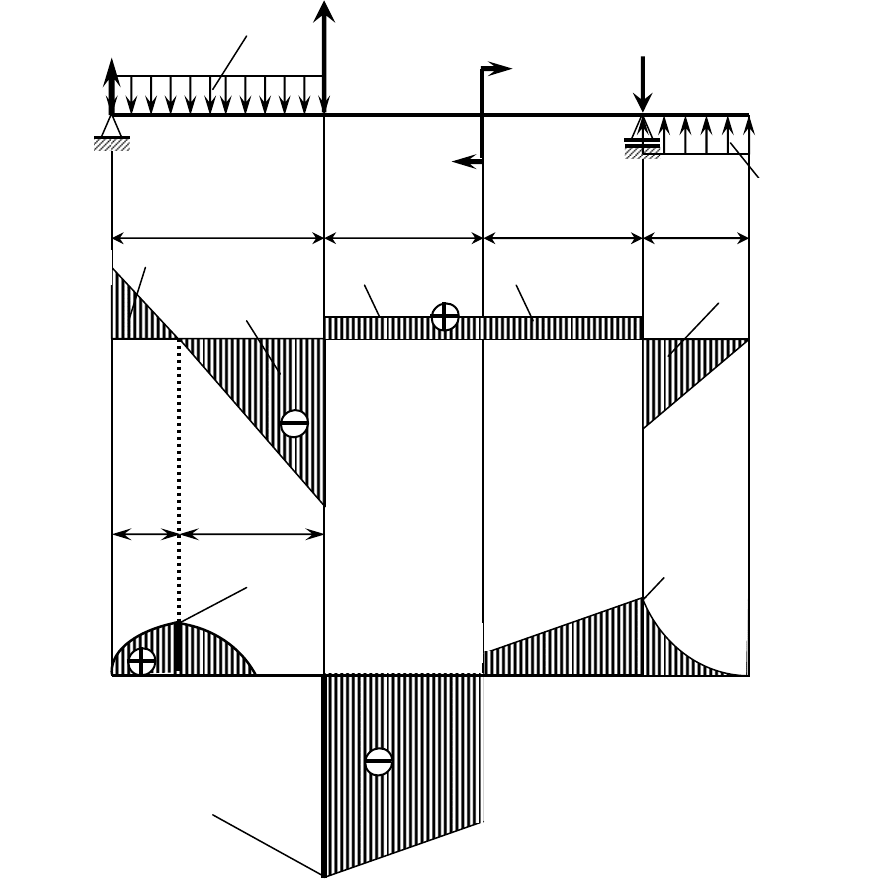
Проверить правильность построения эпюр Q (см. рисунок 6.3).
Рисунок 6.3
а)
б)
в)
4 а
3 а
3 а 2 а
3
R
A
=3 qa
I
D
B
А
Р
m=10 qa
2
q
1
=3q
R
В
=5 qa
II III
2
1
qa
z
0
=a
3qa
0
9qa
Q
y
C E
q
2
= 2 q
IV
4
5
qa
3a
4qa
0
1,5 qa
2
M
x
12 qa
2
9qa
2
4qa
2
qa
2
57
Идём слева направо.
Вычисляем значения Q в характерных сечениях А, С, D, В, Е,
которые ограничивают характерные участки I, II, III, IV.
В сечении А сила R
A
направлена вверх (
А
Q имеет «+»):
À
Q = R
А
= 3qa.
Скачок равен 3qa ; знак «+» (см. пункт 7 выводов).
В конце участка (в сечении на бесконечно близком расстоянии
от сечения С)
C
Q равна
À
Q в начале участка плюс площадь эпюры
от распределённой нагрузки (со знаком «−», так как распределенная
нагрузка направлена вниз):
ëåâ
Ñ
Q = 3qa − 3q ⋅ 4a = −9 qa (пункт 5).
Эпюра Q на I участке имеет вид наклонной прямой (пункт 1).
Так как в сечении С приложена сосредоточенная сила Р = 10qa
и направлена вверх, то Q на границе I и II участков возрастает на ве-
личину 10 qa скачкообразно:
прав
С
Q = −9qa + 10qa = qa (пункт 2).
От начала II участка и до конца III участка поперечная сила ос-
таётся постоянной, так как на этом участке отсутствует распреде-
лённая нагрузка:
прав
С
Q =
лев
B
Q = qa (пункт 1).
В конце III участка на расстоянии, бесконечно близком к сече-
нию
В,
y
Q = qa. В самом сечении приложена сосредоточенная сила
R
В
= −5qa, направленная вниз (отрицательная).
Следовательно, в начале IV участка будет скачок, равный
силе
R
В
:
прав
С
Q = qa − 5qa = −4qa (скачок, пункт 7).
В конце участка IV
E
Q равна
B
Q плюс площадь эпюры рас-
пределённой нагрузки:
E
Q = −4qa + 2q ⋅ 2a = 0 (пункт 5),
E
Q = 0.
Эпюра участка IV представляет собой наклонную прямую
(пункт 2).
Пример решения задачи 12
Проверить правильность построения эпюры М
х
(см. рисунок 6.3).
В любом сечении участка I
y
Q
= R
A
− 3qz.

58
Найдём положение сечения z
0
, где эпюра поперечной силы
y
Q
пересекает линию
Z, т.е.
y
Q
= 0:
R
A
− 3qz
0
= 0, a
q
qa
q
R
z
A
===
3
3
3
0
.
Найдём значения
x
M в характерных сечениях А, С, Д, В, Е и в
сечении при
z
0
= а.
В сечении А:
A
M
= 0.
В сечении
С:
C
M = площадь треугольника 1 минус площадь
треугольника 2 плюс
A
M , т.е.
2
C
qaaqaaaM 12039
2
1
3
2
1
−=+⋅−⋅= (пункт 5).
В сечении С на эпюре
x
M произойдёт излом, так как приложе-
на сосредоточенная сила (пункт 7).
Определим экстремум на участке I (при
z = a):
2
2
0max
5,1
2
33
2
33 qa
a
qaaqa
z
qazqaÌ =⋅⋅⋅=−⋅= .
Значение
max
М = 1,5qa, следовательно, экстремум положитель-
ный (пункт 4).
На эпюре
1
Q :
−
треугольник 1 – положительный, эпюра
x
M возрастает
(пункт 3);
−
треугольник 2 – отрицательный, эпюра
x
M убывает (пункт 3).
Эпюра на участке I имеет выпуклость навстречу распределён-
ной нагрузке (пункт 6).
В сечении
D (слева):
M
D
= площадь прямоугольника 3 + М
С
;
M
D
лев
= qa
⋅
3a − 12qa
2
= 3 qa
2
− 12qa
2
= −9 qa
2
(пункт 5).
В самом сечении
D приложен сосредоточенный момент
m = 10 qa
2
(положительный).
Следовательно, в сечении
D произойдёт «скачок», равный
m = 10 qa
2
.
M
D
прав
= −9qa
2
+ 10qa
2
= qa
2
(пункт 7).
59
Эпюра
x
M на участке II возрастает, так как эпюра
y
Q положи-
тельна (пункт 3).
В сечении
В: М
В
= площадь прямоугольника 4 + M
D
прав
;
М
В
= qa⋅3a + qa
2
= 4qa
2
(пункт 5).
Эпюра
x
M на участке III возрастает, так как эпюра
y
Q положи-
тельна (пункт 3).
В сечении
Е М
Е
= 0. В сечении В произойдёт излом в эпюре,
так как в этом сечении приложена сосредоточенная сила (пункт 7).
На участке IV эпюра
x
M имеет вид параболы, направленной
выпуклостью вниз (пункт 6). Эпюра
x
M на участке IV убывает, так
как эпюра
y
Q отрицательна (пункт 3).
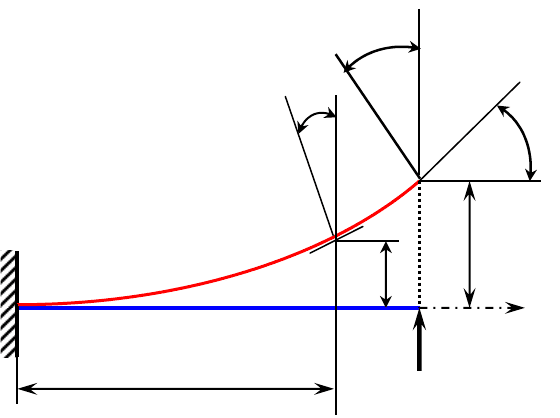
6.3 Перемещения сечений балки
Пояснения к решению задачи 13 (см. приложение А)
Под действием внешних сил, вызывающих прямой изгиб бал-
ки, её первоначальная прямая ось изгибается, превращаясь в кривую
линию, называемую изогнутой осью, или упругой линией балки (ри-
сунок 6.4).
Вследствие изгиба центр тяжести поперечного сечения балки
получает линейное перемещение, перпендикулярное к первоначаль-
ной оси балки, которое называется прогибом сечения
y, а попереч-
ное сечение, оставаясь плоским и перпендикулярным к изогнутой
оси балки, поворачивается вокруг нейтральной оси
Х на угол θ, ко-
торый называется углом поворота сечения.
Рисунок 6.4
y
z
Z
Р
y
z
θ
z
θ
θ

60
Перемещения балки
z
y и
z
θ
, находящиеся на любом расстоя-
нии
z от начала координат, можно определить методом начальных
параметров с помощью обобщённых или универсальных уравнений
упругой линии
*
:
242462
4
2
2
4
1
1
3
2
00
q
i
i
pi
mi
z
zq
zq
zP
zEJEJEJ
q
yy
zm
Σ−Σ+Σ+Σ+θ+=
, (6.4)
662
3
2
2
3
1
1
2
0
q
i
q
i
mi
miz
zqzq
zP
zEJEJ
m Σ−Σ++Σ+θ=θ
, (6.5)
где EJ − жёсткость сечения балки;
z
y
и
z
θ − прогиб и угол поворота сечения балки на расстоянии z
от начала координат;
y
0
и θ
0
− прогиб и угол поворота сечения балки в начале коор-
динат;
m, P и q − внешние нагрузки, приложенные к балке (активные и
реактивные);
z
m
, z
P
, z
q
− расстояния от рассматриваемого сечения до точки
приложения, соответствующей внешней нагрузке (
q
z − до начала
действия соответствующей распределённой нагрузке).
Начало координат необходимо располагать в левом конце бал-
ки, а ось
Z направить вправо (можно наоборот).
Значения начальных параметров
y
0
и θ
0
определяются из гра-
ничных условий или условий поведения балки на опорах.
Если начало координат совпадает с защемлением балки (рису-
нок 6.5,
а), то оба начальных параметра θ
0
и y
0
равны нулю.
*
Метод основан на непосредственном интегрировании основной формулы
теории изгиба балки при использовании специальных приёмов рационального
интегрирования:
− интегрирование выражений, содержащих скобки, проводится без рас-
крытия скобок;
− если на балку действует сосредоточенный момент, то этот момент при
решении уравнения умножают на выражение в скобке, равное 1;
− если на балку действует
распределённая нагрузка, не доходящая до
конца балки, то её продолжают до конца, и для сохранения первоначального
условия прикладывают распределённую нагрузку, равную добавленной, но с
обратным знаком.
