Гонтарь И.Н., Волчихина Н.И. Сопротивление материалов

Подождите немного. Документ загружается.

131

После установки дополнительной опоры в заданной точке

К балка

становится статически неопределимой.

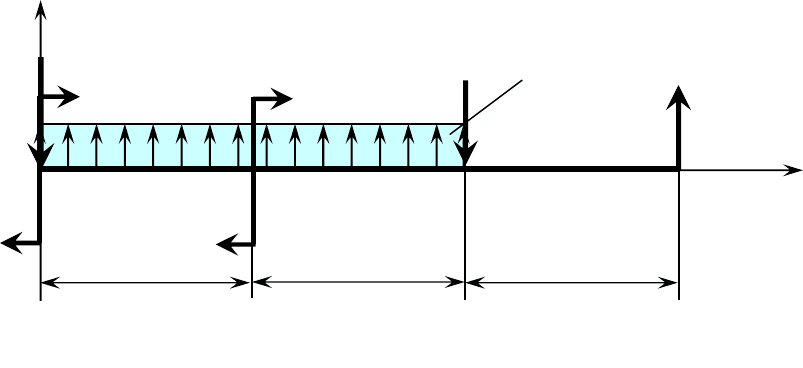
Составляем расчётную схему балки, нагруженной активными и ре-

активными силами (рисунок 4.1.2).

Заменяем действие закреплений балки опорными реакциями.

Произвольно назначаем направление реакций опор Y

, Y

и Y

(см. рисунок 4.1.2).

Составляем моментные уравнения внешних сил относительно

опорных концов балки

А и В.

Для плоской системы сил возможно составить только два уравнения

статики. Остальные превращаются в тождества 0 ≡ 0.

Σm

= 0, – М

+ (q · 2a ) a – M

– Y

· 2a + Y

· 3a = 0. (1)

Σm

= 0, – М

– (q · 2a) 2 а – M

+ Y

· 3a+ Y

· a = 0. (2)

Имеем три неизвестных и два уравнения. Следовательно, балка явля-

ется статически неопределимой системой (СНС).

Степень статической неопределимости

cн

= n

− n

= 3 − 2 = 1.

Раскрываем статическую неопределимость методом сил.

Для раскрытия статической неопределимости необходимо обратиться

к деформационному уравнению.

Для одного раза СНС (n

cн

= 1) каноническое уравнение метода сил со-

держит всего два члена и имеет вид

1111

∆

⋅

EJХEJ

. (3)

Для балки постоянного сечения из одного вида материала EJ

= const

уравнение (3) принимает вид δ

+ ∆

= 0, где δ

– податливость, т. е. пе-

Рисунок 4.1.2 – Расчётная схема трёхопорной балки

А В

132

ремещение в направлении действия силы Х

от действия единичной силы,

приложенной в точке действия приложения силы Х

, это безразмерный си-

ловой коэффициент уравнения; ∆

– перемещение в направлении действия

силы Х

, вызванное всеми внешними силами; это свободный коэффициент

уравнения.

Для раскрытия статической неопределимости выбираем

основную

систему

так, чтобы она была статически определимой и имела геометриче-

ски неизменяемую схему.

Отбросим любую из трёх опор, например, опору

D, и таким образом

получим основную систему (рисунок 4.1.3), которая представляет схему

статически определимой двухопорной балки.

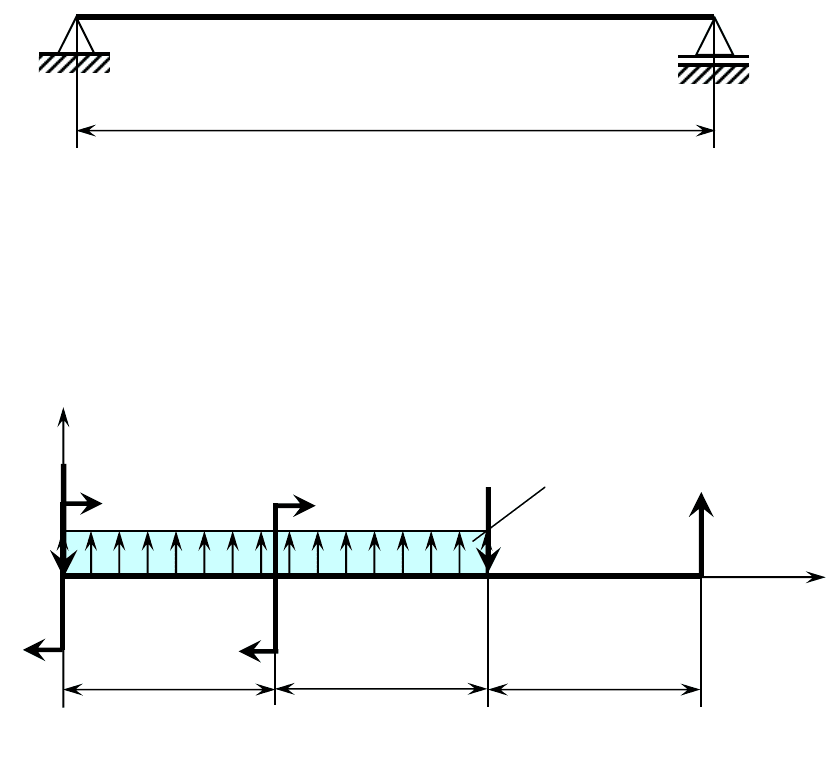
Составляем эквивалентную систему (рисунок 4.1.4), т. е. загружаем

основную систему заданными силами, а неизвестную силу реакции в от-

брошенной опоре заменяем силой Х

Условие эквивалентности – отсутствие прогиба сечения

D, где была

опора, т. е. EJy

= 0.

Рисунок 4.1.4 – Эквивалентная система (ЭС)

ЭС

А В

Рисунок 4.1.3 – Основная система для раскрытия статической

неопределимости балки методом сил (ОС)

ОС

3а

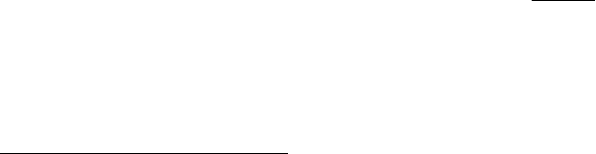
133

Под действием всех приложенных внешних сил, и в том числе си-

лы Х

в эквивалентной балке возникают такие же внутренние усилия, как и

в заданной балке

Для определения коэффициентов канонического уравнения использу-

ем принцип суперпозиции (принцип независимости действия сил).

Загружаем основную систему последовательно:

−

единичной силой Х

(рисунок 4.1.5,б), эта балка имеет два участка;

−

моментами М

, М

и нагрузкой q (рисунок 4.1.5,г).

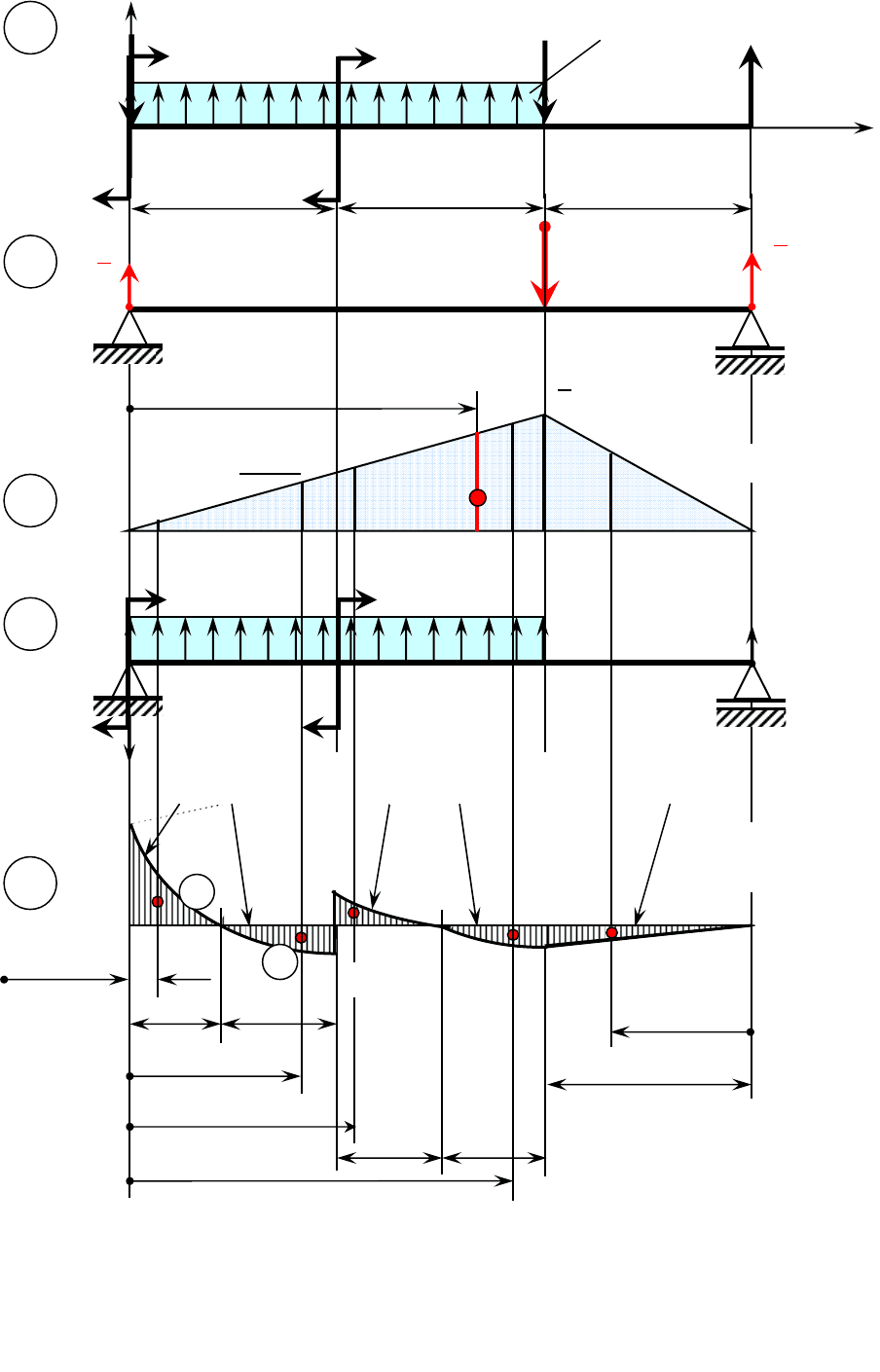
Определяем реакции и изгибающие моменты по схемам рисун-

ка 4.1.5,б,г.

Реакции единичной балки (см. рисунок 4.1.5,б):

momA

= 0; Y

· 6 – 1 · 4 = 0 => Y

= 2/3.

momB

= 0; Y

· 6 – 1 · 2 = 0 => Y

= 1/3.

ΣY =1/3 + 2/3 – 1≡ 0.

Изгибающие моменты на I участке:

в сечении

А z = 0, М

* = 0,

в сечении

D z = 4 м, М

* = 4/3,

где М

*, М

* − моменты единичной балки.

Отсчёт z на II участке справа налево:

в сечении

В z = 0, М

* = 0,

в сечении

D z = 2 м, М

* = 4/3.

Строим отдельно эпюру М* для

единичной балки (рис. 4.1.5,в).

Реакции

грузовой балки с силами М

, М

и q (см. рисунок 4.1.5,г):

momA

= 0; – M

– M

+ q · 4 · 2 – Y

· 6= 0 => Y

= 3,33 кН.

momB

= 0; – M

– M

– q · 4 · 4 + Y

· 6 = 0 => Y

= 76,67 кН.

Изгибающие моменты на I участке: 0 ≤ z ≤ a = 2 м,

zYMM

⋅

+⋅−= ,

сечение

С z = 2 м, М

= – 53,34 кН ⋅ м.

Изгибающие моменты на II участке: 0 ≤ z ≤ a = 2 м.

Новая система становится эквивалентной только в том случае, когда вместо свя-

зей (опор или других видов закреплений) накладываются ограничения линейным или

угловым перемещением или одновременно и тем и другим. Эквивалентная система

(см. рисунок 4.1.3) полностью заменяет заданную трёхопорную конструкцию (см рису-

нок 4.1.4) при условии ограничения перемещения сечения

D, т. е. y

= 0, так как нор-

мальные напряжения σ и вертикальные перемещения ∆ в ней точно такие же.

134

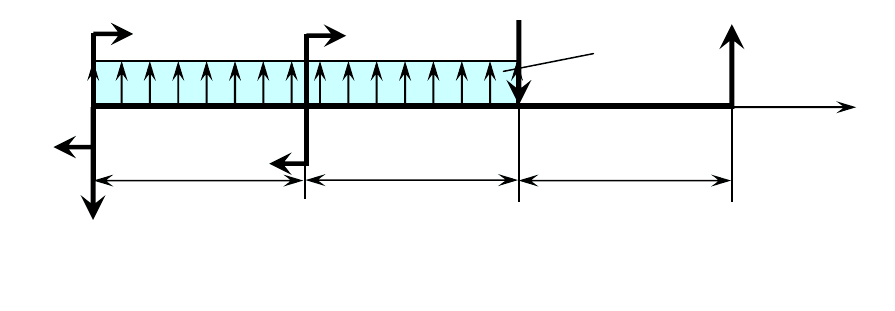
Рисунок 4.1.5 – Расчётные схемы и эпюры

а а

А В

1,21

0,889

z=10/3

0,074

Эпюра М*

0,527

0,75

Ω

23,3

1,33

Ω

0,221

2,0

Эпюра M

кН·м

6,66

–

Ω

26,66

Ω

53,2

3,625

2,25

1,09

0,91

1,0

Ω

53,34

135

Функция изгибающего момента представляет собой квадратную па-

раболу;

в сечении

А z = 0, М

= М

= 60 кН ⋅ м;

(

)

zaq

zYMMM

+⋅−+= .

Функция изгибающего момента также представляет собой квадрат-

ную параболу;

в сечении С z = 0, М

= М

= 26,66 кН ⋅ м;

в сечении

D z = 2 м, М

= – 6,66 кН ⋅ м.

Изгибающие моменты на третьем участке: 0 ≤ z ≤ a = 2 м.

Изменение параметра z справа налево.

= – Y

·z ;

функция изгибающего момента – прямая линия;

в сечении

B z = 0, М

= 0;

в сечении

D z = 2 м, М

= – 6,66 кН ⋅ м.

Определяем коэффициенты δ

и ∆

канонического уравнения (3) по

способу Верещагина, т. е. перемножением эпюр М (М

, М

, q) и М*.

Коэффициент δ

= ω*· η*,

где ω* – площадь эпюры изгибающего момента от единичной силы Х

;

η* – ордината единичной эпюры М*, положение которой совпадает с

центром тяжести площади этой эпюры.

ω* = (1/ 2) L · М*, ω* = (1/2) · 6 · М* = (1/2) 6 (4/3) = 4 м

Определяем положение центра тяжести площади ω* для вычисления

ординаты η*:

ц.т.

= (2 L – а)/3, z

ц.т.

= (2 · 6 – 2) / 3 = 10/3 м.

Ордината η* под центром тяжести площади

единичной эпюры

η* = (1/3) · z

ц.т.

= 10/3 м.

= ω* η* = 4 (10/3) = 40/3 м

Следовательно, можно условно сказать, что мы перемножили единич-

ную эпюру «саму на себя».

Коэффициент ∆

= ΣΩ

· M

где Ω

– площадь простейшей фигуры грузовой эпюры изгибающего момен-

та; M

* – ордината единичной эпюры под центром тяжести площади про-

стейшей фигуры Ω

136

∆

= Ω

· M

* + Ω

· M

* + Ω

· M

*+ Ω

· M

* + Ω

· M

Ω

= (1/3)L

= (1/3) · 0,91 · 60 = 18,2 0,074 кН ⋅ м

где L

– ширина первой фигуры на эпюре М

(рисунок 4.1.4,д);

– ордината изгибающего момента первой фигуры изгибающих

моментов;

* – ордината на эпюре M* под центром тяжести первой фигуры Ω

*= (1/3) · z

; z

= (1/4) L

= (1/4) · 0,91 = 0,221 м;

* = (1/3) · 0,221= 0,074 м;

Ω

· M

* = 18,2 · 0,074 = 1,35 кН ⋅ м

Ω

= – (2/3)L

= (2/3) · 1,09 · 53,34 = – 37,82 кН ⋅ м

;

*= (1/3) · z

; z

= 2 – (3/8) L

= 2 – (3/8) · 1,09 = 1,59 м ;

* = (1/3) · 1,59 = 0,527 м;

Ω

· M

* = – 37,82 ·0,527 = – 20,04 кН ⋅ м

Ω

= – (1/3)L

= – (1/3) · 1,0 · 26,66 = – 8,886 кН ⋅ м

;

*= (1/3) · z

;

= 2 + (1/4) L

= 2 + (1/4) ·1,0 = 2,25 м;

* = (1/3) · 2,25 = 0,75 м;

Ω

· M

* = – 8,886 · 0,75 = – 6,66 кН ⋅ м

Ω

= – (2/3)L

= (2/3) · 1,0 · 6,66 = – 4,44 кН ⋅ м

*= (1/3) · z

; z

= 4 – (3/8) L

= 4 – (3/8) ·1,0 = 3,625 м,

* = (1/3) · 3,625 = 1,21 м.

Ω

· M

* = – 4,44 · 1,21 = – 5,37 кН ⋅ м

Ω

= – (1/2)L

= (1/2) · 2,0 · 6,66 = – 6,66 кН ⋅ м

*= (2/3) · z

, z

= (2/3) L

= (2/3) · 2,0 = 4/3 м,

* = (2/3) · (4/3) = 0,889 м,

Ω

· M

* = – 6,66 · 0,889 = –5,92 кН ⋅ м

∆

= 1,35 – 20,04 + 6,66 – 5,37 – 5,92 = 23,3 кН ⋅ м

2,5

93,23

⋅

∆

X кН, следовательно, Y

= X

= 5,2 кН.

Подставляем найденное значение Y

в уравнения статики (1) и (2).

Откуда получаем Y

= 74,9 кН и Y

= 0,1 кН.

Проверка. Σ Y = 0. – Y

+ q·2а − Y

– Y

= 0; – 74,9 +20 · 4 − 5,2 +

+ 0,1 = 0.

Сумма проекций всех вертикальных сил на ось Y обратилась в нуль,

но не тождественно.

137

Поскольку исходные данные заданы с одной значащей цифрой до за-

пятой, то можно округлить значения результатов расчёта.

В таком случае следует считать

= 75,0 кН, Y

= 0 и Y

= 5,0 кН.

Статическая неопределимость раскрыта, так как определены все неиз-

вестные внешние силы.

Проверяем правильность раскрытия статической неопределимости.

Проверка решения силовых уравнений статики (1), (2), (3) показыва-

ет, что арифметические вычисления выполнены верно, но необходимо сде-

лать деформационную проверку, выбрав другую

основную систему. На-

пример, заменив опору

В безразмерной силой Х

(рисунок 4.1.6).

Проверочное решение новой системы проводим аналогично изложен-

ной методике раскрытия статической неопределимости.

Принимаем основную систему по схеме рисунка 4.1.7,а.

Прикладываем в сечении

В основной системы единичную сосредото-

ченную силу Х

(рисунок 4.1.7,б).

Определяем реакции

Σm

= 0, – Y

· 2a + 1 · 3a = 0, Y

= 3/ 2.

Σm

= 0, –Y

· 2a + 1 · a = 0, Y

= 1/ 2.

Ординаты единичной балки z = 0 M* = 0,

z = 4 м, M* = (1/2) · 4 = 2 м, z = 6 м, M* = 0.

Строим

единичную эпюру M* (рисунок 4.1.7,в).

Для простоты расчёта используем принцип суперпозиции, т. е.

грузо-

вую

балку нагружаем отдельно равномерно распределённой нагрузкой q

(рисунок 4.1.7,г) и отдельно каждым моментом М

(рисунок 4.1.7,е)

и М

(рисунок 4.1.7,з).

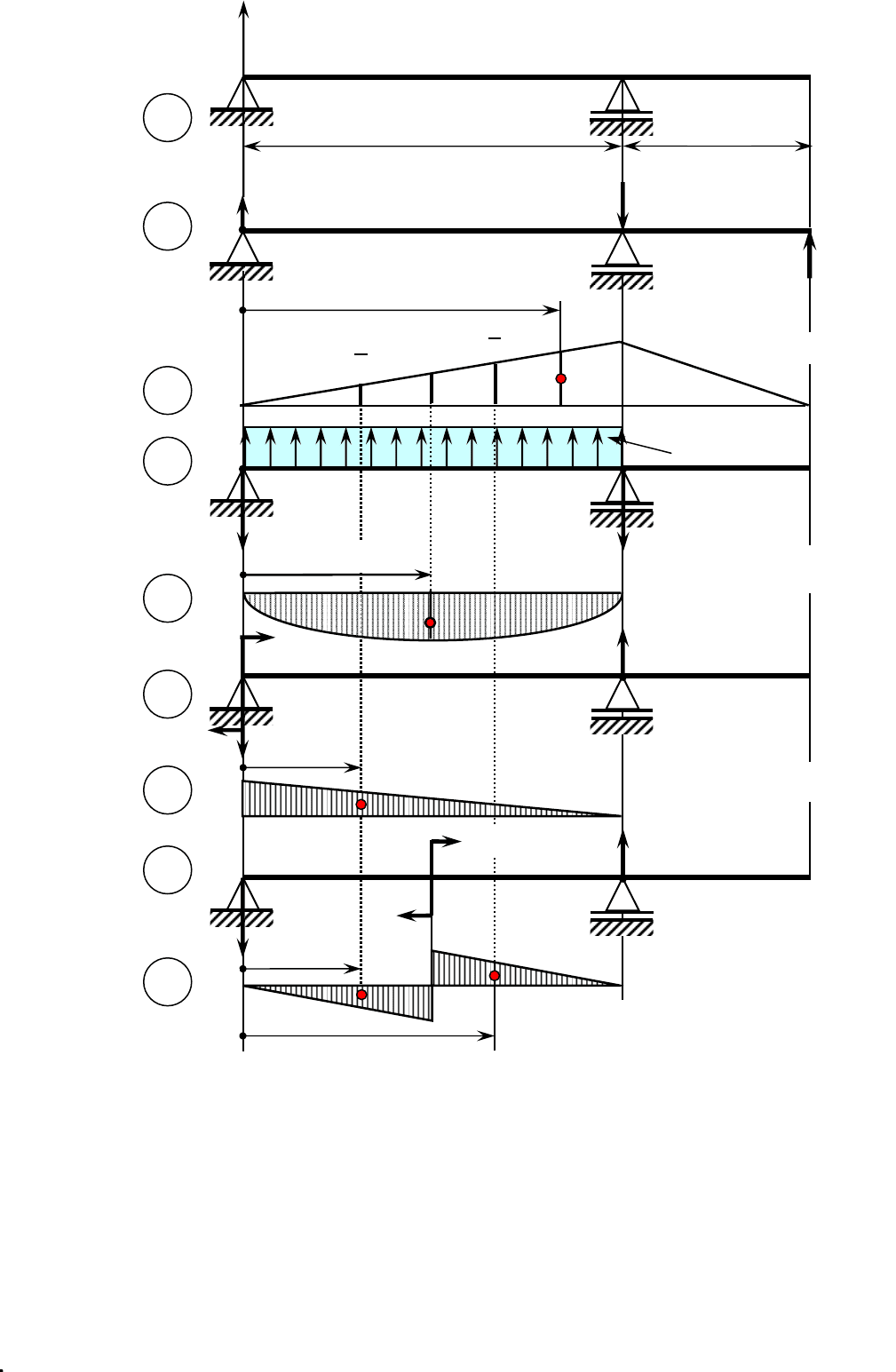
Рисунок 4.1.6 – Схема второй эквивалентной балки для деформационной

проверки раскрытия статической неопределимости

ЭС

138

ОС

2а а

0,5

1,5

40 кН

Эпюра М

(q)

Эпюра М*

Эпюра М

)

Эпюра М

)

Рисунок 4.1.7 – Расчётные схемы и эпюры для деформационной проверки раскрытия

статической неопределимости

139

Составляем функции изгибающих моментов по участкам и строим

эпюры М

(q), М

(М

), М

(М

) отдельно для каждой внешней нагрузки (ри-

сунок 4.1.7,д,ж,и соответственно).

Расчёт эпюры М

(q).

Реакции. Σm

= 0, (q · 2a ) a – Y

· 2a = 0 => Y

= q · a = 40 кН.

В силу симметрии Y

= q · a = 40 кН.

Изгибающие моменты М

= – Y

+ q · z

/2 .

Функция М

является квадратной параболой.

Строим эпюру М

(q) (см. рисунок 4.1.7,д).

Расчёт эпюры М

(М

Реакции. Σm

= 0, –М

+ Y

· 2a = 0 => Y

= М

/2a = 15 кН.

Σm

= 0, –М

· 2a = 0 => Y

= М

/2a = 15 кН.

Изгибающие моменты М

= М

– Y

· z.

z = 0, М

= М

= 60 кН ⋅ м.

z = 2а , М

= 0.

Функция изгибающего момента – прямая линия.

Строим эпюру М

(М

) (см. рисунок 4.1.7,ж).

Расчёт эпюры М

(М

Реакции. Σm

= 0, – М

· 2a = 0 => Y

= М

/2a = 20 кН.

Σm

= 0, –М

· 2a = 0 => Y

= М

/2a = 20 кН.

Изгибающие моменты М

= М

– Y

· z.

Имеем два участка:

I участок: z = 0, М

= 0, z = а, М

= – 40 кНм.

II участок: z = 0, М

= + 40 кНм, z = а, М

= 0.

Функция изгибающего момента изменяется по прямой со скачком в

сечении

С при z = a. Строим эпюру М

(М

) (см. рисунок 4.1.7,и).

Вычисляем коэффициенты δ

и ∆

1Р

деформационного уравнения (3).

Единичный коэффициент δ

= ω·η; 626

=⋅⋅==ω Lh м

; *

z⋅= .

Для неравностороннего треугольника (см. рисунок 4.1.7,в) положение

центра тяжести вычисляем по формуле

)262(

)2(

* =−⋅=−= aL

z м;

η =⋅= м;

=⋅=δ м

Грузовой член ∆

1Р

вычисляем как сумму ∑Ω

· М

140

По эпюрам на рисунке 4.1.7,д и в

320

404

111

−=⋅⋅−=−=Ω hL кН ⋅ м

;

11111

==== МLzzМ м;

320

−=⋅−=Ω М кН ⋅ м

По эпюрам на рисунке 4.1.7,ж и в

120604

222

=⋅⋅==Ω hL кН ⋅ м

;

222222

==⋅===== ММLzzМ м;

240

120

=⋅=Ω М кН ⋅ м

По эпюрам на рисунке 4.1.7,и и в

40402

333

−=⋅⋅−=−=Ω hL

кН ⋅ м

;

33333

=⋅===== МLzzМ м;

−=⋅−=Ω М кН ⋅ м

40402

444

+=⋅⋅==Ω hL кН ⋅ м

44444

=⋅==⋅+=

⎟

⎠

⎞

⎜

⎝

⎛

+== МLаzzМ м.

160

=⋅=Ω М кН ⋅ м

160

240

320

****

443322111

≡+−+−=Ω+Ω+Ω+Ω=∆ ММММ

Грузовой член ∆

1Р

тождественно равен нулю, следовательно, из

уравнения (3) имеем

=Х => Y

= 0.

Это означает, что на опору

В не передаются усилия от внешних

нагрузок. Они воспринимаются двумя опорами

А и D.

Решая уравнения ( 1) и (2), получим Y

= 75,0 кН и Y

= 5,0 кН.

Деформационная проверка полностью подтвердила правильность

вычислений при раскрытии статической неопределимости.

Составляем расчётную схему балки с действительными направле-

ниями реакций Y

, Y

и Y

(рисунок 4.1.8).

Строим эпюры Q

и M