Гласман К.Ф., Покопцева М.Н. Цифровые устройства и микропроцессоры (часть 1)

Подождите немного. Документ загружается.

СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ

= 1000 0111

2-10

Такой код называют натуральным двоично-десятичным кодом (слово

“натуральный” часто опускают). Его разряды имеют весовые

коэффициенты 1, 2, 4, 8, 10, 20, 40, 80 и т.д.

Двоично-десятичный код обладает избыточностью. Его применение

неэффективно с точки зрения полноты использования двоичных

комбинаций. Но он очень удобен при вводе и выводе данных в десятичной

форме.

1.3 Унитарный код

Унитарный n-разрядный код каждому числу m от 0 до (n - 1) ставит в

соответствие кодовую комбинацию длиной n. Разряд комбинации,

занимающий позицию с номером m, равен 1, остальные разряды равны 0.

Такой код имеет также название "1 из n". Кодовые комбинации,

представляющие числа от 0 до 9, приведены в таблице. 1.2.

Таблица 1.2

0 0 0 0 0 0 0 0 0 1

0 0 0 0 0 0 0 0 1 0

0 0 0 0 0 0 0 1 0 0

0 0 0 0 0 0 1 0 0 0

0 0 0 0 0 1 0 0 0 0

0 0 0 0 1 0 0 0 0 0

0 0 0 1 0 0 0 0 0 0

0 0 1 0 0 0 0 0 0 0

0 1 0 0 0 0 0 0 0 0

1 0 0 0 0 0 0 0 0 0

Унитарный код используется для представления данных при их вводе

в цифровые устройства (например, с помощью клавиатуры) и при

отображении результатов с помощью индикаторов.

1.4 Код Грея

Во многих практических приложениях, например, при аналоговом

цифровом преобразовании сигналов, желательно использовать коды, в

которых все последовательные кодовые комбинации отличаются друг от

друга лишь одним разрядом. Такие коды называют циклическими.

ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1

Наиболее часто применяется циклический код Грея. Это обусловлено

простотой процедуры перехода от двоичного числа к такому коду.

Четырехразрядный код Грея приведен в табл. 1.3.

Таблица 1.3

Код Грея Двоичный код

Десятичное

число

0 0 0 0 0 0 0 0 0

1 0 0 0 1 0 0 0 1

2 0 0 1 1 0 0 1 0

3 0 0 1 0 0 0 1 1

4 0 1 1 0 0 1 0 0

5 0 1 1 1 0 1 0 1

6 0 1 0 1 0 1 1 0

7 0 1 0 0 0 1 1 1

8 1 1 0 0 1 0 0 0

9 1 1 0 1 1 0 0 1

10 1 1 1 1 1 0 1 0

11 1 1 1 0 1 0 1 1

12 1 0 1 0 1 1 0 0

13 1 0 1 1 1 1 0 1

14 1 0 0 1 1 1 1 0

15 1 0 0 0 1 1 1 1

Пусть - кодовое слово в коде Грея с разрядами, а

- соответствующее двоичное число, где индексы 0 и ( )

обозначают младший и старший разряды соответственно. Тогда разряды

кода Грея выражаются через биты двоичного числа следующим образом:

01221

... ggggg

nn −−

01221

... bbbbb

nn −−

1−n

11 −−

; ;

⊕=

iii

bbg

−

≤

где ⊕ - символ операции Исключающее ИЛИ:

0 ⊕ 0 = 0; 0 ⊕ 1 = 1; 1 ⊕ 0 = 1; 1 ⊕ 1 = 0.

Для определения бита при преобразовании кода Грея в двоичное

число необходимо найти количество единиц в разрядах . Если

число единиц четно, то , если нечетно – то

11 ++

−

gb =

1.5 Код Джонсона

Кодовые комбинации кода Джонсона (табл. 1.4) отличаются друг от

друга только в одном разряде. Он известен также под названием

СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ

заполняющего кода. Это название связано с тем, что разряды кода,

первоначально равные нулю, последовательно "заполняются" сначала

единицами, а затем нулями (начиная с младшего разряда).

Таблица 1.4

0 0 0 0 0

0 0 0 0 1

0 0 0 1 1

0 0 1 1 1

0 1 1 1 1

1 1 1 1 1

1 1 1 1 0

1 1 1 0 0

1 1 0 0 0

1 0 0 0 0

Код Джонсона легко преобразуется в унитарный код "1 из 10" по

значениям двух разрядов, находящихся на границе "волн нулей" и "волн

единиц" (для m=0 и m=5 такими пограничными разрядами являются

400

xxy ⋅=

405

xxy

⋅

101

xxy ⋅=

106

xxy

⋅

212

xxy ⋅=

217

xxy

⋅

323

xxy ⋅=

328

xxy

⋅

434

xxy ⋅=

439

xxy

⋅

здесь - разряды кода "1 из 10".

В таком пятиразрядном коде работают десятичные счетчики

Джонсона.

1.6 Представление чисел со знаком

Существует несколько способов представления положительных и

отрицательных чисел, выраженных в двоичном коде. Один из них

предполагает представление числа посредством знака и величины, причем

бит знака занимает самый старший разряд. Остальные разряды отводятся

для представления абсолютной величины числа. Если оно положительное,

бит знака S равен 0, если оно отрицательное, то этот бит, равен 1. Такая

форма представления определяет код числа:

[] [ ]

⎩

⎨

⎧

≤

≥

==±=

−

−−

;0,1

;0,0

011

011011

Аеслиaaа

Аеслиaaa

aaaSaaаА

ПК

где - последовательность, представляющая в двоичном коде

абсолютную величину -разрядного числа.

011

... aaa

n−

Прямой код используется при выводе чисел на индикацию, при вводе

данных, но он плохо подходит для вычислений. В нем существуют нули в

двух формах (+0 и -0, определяемые соответственно как 0000 и 1000). При

четырех разрядах, отведенных для представления числа, в прямом коде

могут быть выражены числа от -7 до +7 включительно (таблица 1.5).

Таблица 1.5

Число Прямой код Код со смещением

Дополнительный

код

-8 - 0000 1000

-7 1111 0001 1001

-6 1110 0010 1010

-5 1101 0011 1011

-4 1100 0100 1100

-3 1011 0101 1101

-2 1010 0110 1110

-1 1001 0111 1111

0 0000 1000 0000

1 0001 1001 0001

2 0010 1010 0010

3 0011 1011 0011

4 0100 1100 0100

5 0101 1101 0101

6 0110 1110 0110

7 0111 1111 0111

Числа со знаком могут также быть представлены в коде со

смещением. Последовательность всех чисел в коде со смещением, начиная

со старшего отрицательного и кончая старшим положительным,

представляет собой двоичную арифметическую прогрессию. Для

получения кодовой комбинации какого-либо числа нужно прибавить к

нему число, равное 2

(здесь (n+1) число разрядов кодового слова), и

представить результат в двоичном коде. Старшее отрицательное число

имеет код 0000, а самое большое положительное - 1111 (см. табл. 1.5).

Нуль в этом коде имеет однозначное представление. Коды положительных

ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1

СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ

и отрицательных чисел отличаются старшим разрядом. Используется код

со смещением в аналого-цифровых и цифро-аналоговых преобразователях.

Наиболее удобен для выполнения арифметических операций с

целыми числами дополнительный код (см. табл. 1.5). Положительные

числа при этом способе представления записываются как числа в прямом

коде. Для того чтобы получить кодовую комбинацию отрицательного

числа, нужно образовать обратный код равного ему по модулю

положительного числа и добавить к полученному результату единицу.

Обратный код

образуется следующим образом:

[] [ ]

⎩

⎨

⎧

≤

≥

=±=

−

;0,1

;0,0

011

Аеслиaaа

Аеслиaaa

aaаА

ОК

где

- инверсия величины .

Прямой и обратный коды положительных чисел совпадают. Для

отрицательных чисел:

(

)

011011011

12111 aaаaaаaaа

KKKK

−−−

−−=−=

т.е. сумма чисел каждого разряда прямого и обратного кода

отрицательных чисел равна 1 (без учета знакового разряда).

Дополнительный код числа

записывается следующим образом:

[] [ ]

⎩

⎨

⎧

≥

=±=

−

;0,

~~~

;0,0

011

Аеслиaaа

Аеслиaaa

aaаА

ДК

где

011011011

aaаaaаaaа

KKK

−−−

−=+=

Если для представления числа отводится (n + 1) двоичных разрядов (n

- для абсолютной величины и 1 - для знака), то в дополнительном коде

можно записать 2

n+1

чисел: (2

-1) положительных, нуль и 2

отрицательных. Нуль в дополнительном коде представлен единственным

образом, старший разряд несет информацию о знаке. Правило образования

дополнительного кода обратимо. Если найти дополнительный код числа,

представленного в дополнительном коде, то получится прямой код этого

числа.

Арифметические операции в дополнительном коде выполняются

весьма просто. Для того чтобы получить сумму двух чисел, надо сложить

соответствующие разряды с учетом переноса. Все разряды, (включая

знаковый) обрабатывается одинаково. Перенос из знакового разряда

игнорируется. Для выполнения вычитания надо вычитаемое представить в

дополнительном коде и сложить с уменьшаемым. Если сумма имеет 1 в

знаковом разряде, то она представляет собой отрицательное число. Если

складываются числа одного знака, а сумма имеет другой знак, то в

дополнительном коде происходит выход за пределы изображения чисел

при данном числе разрядов, что эквивалентно ошибке. На это должен

указывать специально формируемый признак.

1.7 Коды с обнаружением ошибок

При передаче, обработке и записи данных нельзя полностью

исключить возможность появления ошибок, возникающих из-за сбоев в

работе аппаратуры или помех, поэтому часто используются такие способы

кодирования данных, при которых можно определять возникновение

ошибок.

Простейший способ распознавания одиночной ошибки заключается в

добавлении к информационным разрядам контрольного бита проверки на

четность р (бит паритета). Этот бит можно формировать двумя способами.

При первом способе в контрольный разряд записывается 0, если число

единиц в информационном слове четное. Если число единиц нечетное, то в

контрольный разряд записывается 1. При этом общее количество единиц в

кодовом слове, включая контрольный разряд, всегда оказывается четным

(четный паритет).

Второй способ предлагает такое формирование контрольного разряда,

при котором общее количество единиц в кодовом слове является нечетным

(нечетный паритет).

В табл. 1.6 приведен двоично-десятичный код с обнаружением

единичной ошибки (контрольный разряд сформирован в соответствии с

условием четного паритета). Единичная ошибка в кодовом слове приведет

к тому, что паритет будет нарушен (количество единиц станет нечетным).

Поэтому проверка кодового слова на четность (вместе с контрольным

разрядом) позволяет зафиксировать ошибку. Может быть также

обнаружено нечетное число ошибок, большее 1. При четном числе ошибок

паритет сохраняется, и они не фиксируются.

Принцип обнаружения ошибок может быть также пояснен

следующим образом. Из пяти двоичных разрядов можно образовать 32

кодовых комбинации. Но, используются в коде (табл. 1.6), т.е. являются

допустимыми, только десять. Остальные кодовые комбинации являются

недопустимыми. Как следует из табл.1.6, любые две допустимые

комбинации отличаются друг от друга, по крайней мере, в двух разрядах.

Поэтому единичная ошибка переводит допустимую комбинацию в

недопустимую. Появление в потоке данных недопустимой кодовой

комбинации и указывает на ошибку, т.е. позволяет ее обнаружить.

ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1

СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ

Таблица 1.6

Кодовое слово

Десятичная

цифра

0 0 0 0 0 0

1 0 0 0 1 1

2 0 0 1 0 1

3 0 0 1 1 0

4 0 1 0 0 1

5 0 1 0 1 0

6 0 1 1 0 0

7 0 1 1 1 1

8 1 0 0 0 1

9 1 0 0 1 0

Число несовпадающих разрядов определяет кодовое расстояние

между двумя словами. Минимальным кодовым расстоянием называется

наименьшее число разрядов, в которых различаются любые две кодовые

комбинации. Например, в двоичном, двоично-десятичном,

дополнительных кодах минимальное расстояние равно 1. Искажение

любого разряда приводит к ошибке, которую нельзя обнаружить. В коде,

приведенном в табл. 1.6, минимальное расстояние равно 2. Очевидно, что

код является кодом с обнаружением ошибок тогда и только тогда, когда

его минимальное расстояние не меньше двух.

1.8 Коды с исправлением ошибок

Для того чтобы код позволял исправлять ошибки, необходимо

увеличивать его минимальное расстояние. Если минимальное кодовое

расстояние равно трем, то любая одиночная ошибка переводит

допустимую кодовую комбинацию в недопустимую, находящуюся на

расстоянии, равном единице от исходной комбинации, и на расстоянии,

больше или равном двум от любой другой допустимой кодовой

комбинации. Поэтому в коде с минимальным расстоянием, равном трем,

можно исправить любую одиночную ошибку.

Рассмотрим основные принципы построения часто используемого

кода Хэмминга, позволяющего исправлять одиночную ошибку. К каждой

группе из m информационных разрядов, представляющих собой

сообщение, присоединяются k контрольных разрядов p

, p

,…, p

проверки на четность. Затем присваивают десятичный номер позиции

каждого из (m + k) разрядов кодовой комбинации, начиная со значения 1

для старшего разряда и кончая значением (m + k) для младшего.

Производится k проверок на четность числа единиц в выбранных разрядах

каждой кодовой комбинации. Результат каждой проверки записывается в

виде 0, если число единиц четное (ошибки нет), и в виде 1 , если число

единиц нечетное (произошла ошибка). По результатам проверки

составляется двоичное число c

, c

, … c

, десятичный эквивалент которого

равен номеру позиции разряда, где произошла ошибка. Если это число

равно 0, то ошибка отсутствует. После того, как обнаружен ошибочный

разряд, его можно исправить путем инверсии.

Число контрольных разрядов можно определить следующим образом.

Используя k разрядов, можно задать 2

двоичных комбинаций. Нулевая

комбинация указывает на отсутствие ошибки, десятичные эквиваленты

остальных должны определять номера позиций любого из (m + k)

разрядов. Следовательно, число k должно удовлетворять неравенству:

≥ m + k + 1.

Из этого неравенства следует, что доля контрольных разрядов в

общей длине кодовой комбинации тем меньше, чем больше число

информационных разрядов.

Для того, чтобы контрольные разряды проверки на четность

определять лишь через информационные разряды и независимо друг от

друга, их размещают в позициях 1, 2, ... 2

k-1

. На остальных позициях

находятся биты, представляющего код исходного сообщения.

В табл. 1.7 и 1.8 показан пример построения кода Хэмминга при

четырех информационных разрядах (m=4, k=3). Контрольные разряды

должны задаваться так, чтобы номер позиции соответствовал положению

ошибочного бита. Если ошибка появляется в позициях 1, 3, 5, 7, то

младший разряд номера позиции, т.е. c

должен равняться единице. Если

код построен так, то в каждой кодовой комбинации сумма битов в

позициях 1, 3, 5, 7, четная и появление одиночной ошибки в любой из этих

позиций приведет к нечетному числу единиц в указанных позициях. В

этом случае младший разряд номера позиции принимается равным 1. Если

ошибки нет, то сума единиц в указанных позициях остается четной, и c

полагается равным 0. Таким образом, p

выбирается так, чтобы установить

четное число единиц в позициях 1, 3, 5, 7. Рассуждая аналогичным

образом, нетрудно прийти к выводу, что p

выбирается так, чтобы четным

было число единиц в позициях 2, 3, 6, 7, а p

должен обеспечить четность

числа единиц в позициях 4, 5, 6, 7.

ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1

СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ

Таблица 1.7

Номера позиций

Номер позиции

Позиция ошибки

0 (Ошибки нет) 0 0 0

1 0 0 1

2 0 1 0

3 0 1 1

4 1 0 0

5 1 0 1

6 1 1 0

7 1 1 1

Таблица 1.8

Код Хемминга

Кодовое слово

Позиция

Десятичная

цифра

1 2 3 4 5 6 7

0 0 0 0 0 0 0 0

1 1 1 0 1 0 0 1

2 0 1 0 1 0 1 0

3 1 0 0 0 0 1 1

4 1 0 0 1 1 0 0

5 0 1 0 0 1 0 1

6 1 1 0 0 1 1 0

7 0 0 0 1 1 1 1

8 1 1 1 0 0 0 0

9 0 0 1 1 0 0 1

Рассмотрим пример обнаружения положения ошибки и ее

исправления. Пусть, например, передана кодовая комбинация 1101001

(сообщение - число 1), но из-за ошибки принято слово 1101101. Проверка

на четность в позициях 4, 5, 6, 7 дает с

=1. В позициях 2, 3, 6, 7 число

единиц четное, поэтому с

=0. Проверка числа единиц в позициях 1, 3, 5, 7

обуславливает с

=1. Получен номер 101, что означает ошибку в пятой

позиции. Инверсия пятого разряда позволяет получить правильное кодовое

слово.

Минимальное расстояние построенного кода Хэмминга равно трем.

Следовательно, он позволяет исправить только одиночную ошибку.

Ненулевая вероятность одиночной ошибки в кодовом слове существует в

любой цифровой аппаратуре. Вероятность возникновения двух и более

ошибок значительно меньше. Поэтому код Хэмминга имеет большое

значение. Он часто применяется при передаче и записи данных для защиты

информации.

1.9 Форматы кодов

Каждый бит кодового слова передается или записывается с помощью

дискретных сигналов, например, импульсов. Как было отмечено выше,

способ представления исходного кода определенными сигналами

определяется форматом кода. Известно большое количество форматов,

каждый из которых имеет свои достоинства и недостатки и предназначен

для использования в определенной аппаратуре. Часто используемые

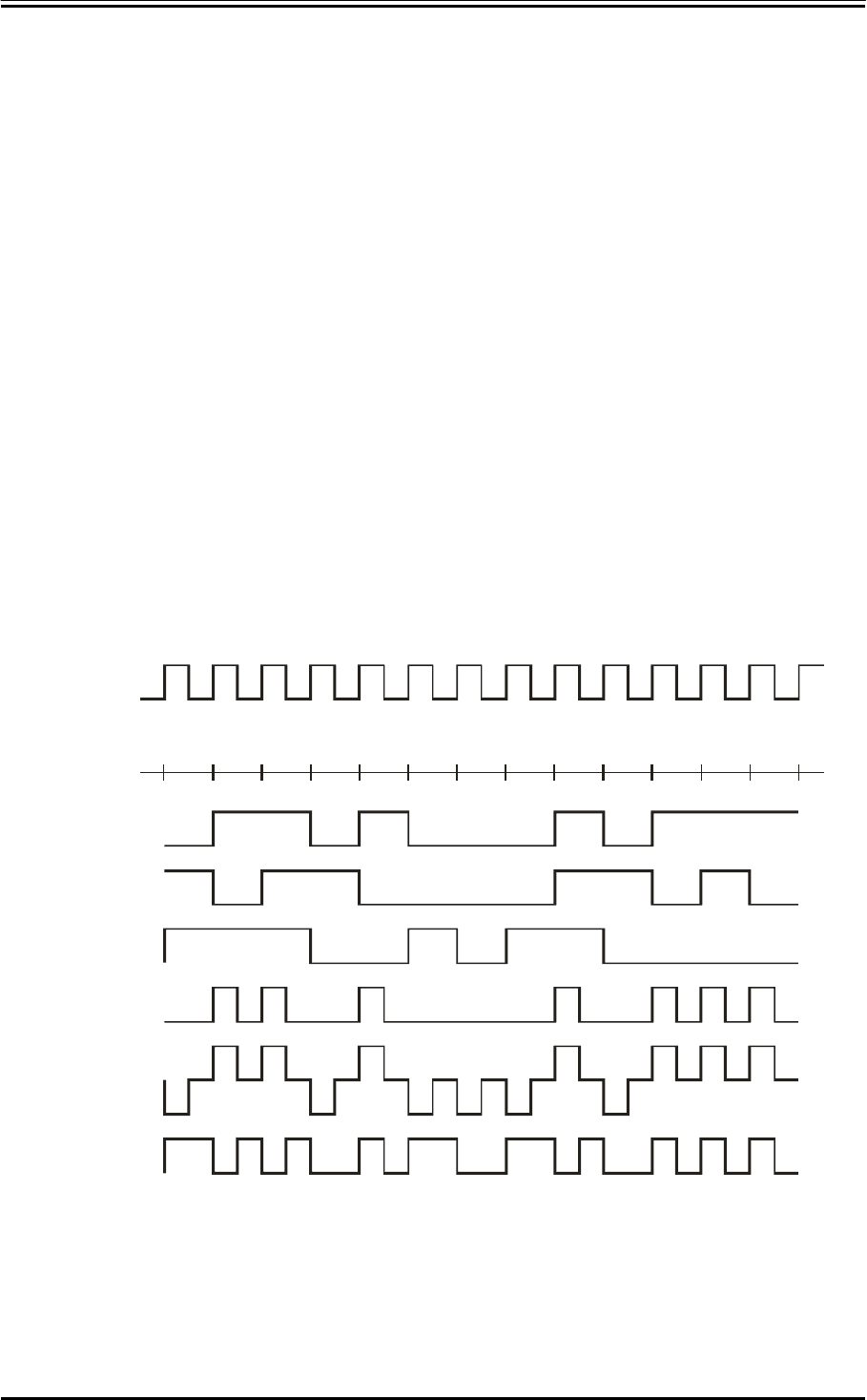
форматы приведены на рис. 1.1. Первая диаграмма рисунка показывает

тактовые импульсы C, вторая - последовательность битов D,

определяющая кодовое слово данных. Остальные диаграммы

иллюстрируют представление исходного кода в различных форматах.

БВН

БВН-1

БВН-0

ВН

ВН-П

ДФ-0

0110100010111

Рис.1.1. Форматы кодов.

Формат БВН (без возвращения к нулю) естественным образом

соответствует режиму работы логических схем. Единичный бит передается

ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1