Giga Y. Surface Evolution Equations: A Level Set Approach

Подождите немного. Документ загружается.

188 Chapter 4. Classical level set metho d

actions {S

}.IfS

⊂ D

for small h>0, then D is regular. The condition

⊂ D

is fulﬁlled if the generator of S

is negative on ∂D

We give another example of such a situation. For a set G in R

× [0, ∞), let

(G)denote

(G)={(λx, λ

m+1

t); (x, t) ∈ G},

where m ∈ R, λ>0. Similarly, for a set G

in R

let D

λ,0

)denote

λ,0

)={λx, x ∈ G

The condition D

1−h,0

) ⊂ G

for small h>0 is a kind of starshapedness.

Theorem 4.5.9 (Dilation invariant equations). Assume that f in (4.1.1) is inde-

pendent of x and t. Assume that f(p, Q

(X)) is positively homogeneous of degree

m ∈ R in Q

(X), i.e.,

f(p, µQ

(X)) = µ

f(p, Q

(X)),µ>0

for all (p, Q

(X)) ∈ E. Assume (W). Let D

be a bounded open set in R

.If

1−h,0

) ⊂ D

for suﬃciently small h>0,thenD is regular, where D is an

open evolution with initial data D

Proof. Let F be the operator deﬁned by (4.1.3). By homogeneity of f we have

F (µp, µ

X)=µ

m+1

F (p, X),µ>0.

Let E be the closed evolution with initial data

. Then by homogeneity of F the

set D

1−h

(E) is a closed evolution with initial data D

1−h,0

). Sending h to zero

yields E ⊂

D.SinceD ⊂ E is trivial, D is regular. 

Corollary 4.5.10. Assume the same hypotheses of Theorem 4.5.9 concerning f .

Let D

be a smoothly bounded domain such that x, n > 0 on ∂D

.LetD be the

open evolution with initial data D

.ThenD is regular.

Proof. Since −x, n is the generator of group {D

−q

} at q = 0, it is clear that

1−h,0

) ⊂ D

for small h>0. Thus D is regular by Theorem 4.5.9. 

We give another criterion when f is rotationally symmetric in the sense that

Rx,t,Rp,

(X)R)=f (x, t, p, Q

(X))

for any rotation matrix R. As well known, a one parameter group {R(λ)} of ro-

tation is generated by a skew-symmetric matrix so it is of form {e

λA

}

λ∈R

with

skew-symmetric matrix A. Similarly to Theorem 4.5.9 we see that if f is rotation-

ally symmetric, e

λA

) ⊂ D

for small λ>0 implies the regularity of D.The

condition e

λA

) ⊂ D

is fulﬁlled if Ax, n < 0on∂D

if D

is smooth. Below

we give a criterion for regularity when f is independent of t, x, dilation invariant

and rotationally symmetric.

4.5. Various properties of evolutions 189

Corollary 4.5.11. Assume the same hypotheses of Theorem 4.5.9 concerning f .

Assume moreover, f is rotationally symmetric. Assume that D

is a smoothly

bounded domain. Assume that there is a nonnegative constant c

andaskew-

symmetric matrix A such that

f(n, ∇n)+Ax, n−c

x, n < 0 on ∂D

Then an open evolution D with initial data D

is regular.

Proof. The condition on ∂D

guarantees that

1−c

h,0

)(D

) ⊂ D

for small h>0. By invariance of the equation E

= D

1−c

(E) is a closed

evolution if E is the closed evolution with initial data

.BycomparisonE

(t +

h) ⊂ D(t), t ≥ 0 for small h>0. In other words

(t) ⊂ D(t − h)fort − h ≥ 0

for small h.Since

D is left continuous and E

(t) → E(t)ash → 0, we see E ⊂ D.

Thus D is regular. 

Finally, we give another type of regularity criterion for orientation-free equa-

tions when an open evolution is a disjoint sum of regular open evolutions.

Lemma 4.5.12. Assume (W) and (4.1.1) is orientation-free. Let U be a bounded

open set in R

that may be written as the union of a ﬁnite number of disjoint

open sets U

,...,U

. Denote the open evolutions with initial data U and U

by D

and D

, respectively (1 ≤ i ≤ k).LetE

be the closed evolution with initial data

and assume that E

= D

Assume that there is a sequence of open covers {U

,...,U

}

α≥1

of U which

satisﬁes:

(i) U

⊃ U

α+1

and U

= ∩

α≥1

for i =1, ..., k;

(ii) the sets U

,...,U

are pairwise disjoint for α ≥ 1.

Finally, let E be a closed evolution for which a double sequence {t

α,

}

α,≥1

exists

such that t

α,

↓ 0 as  →∞and

E(t

α,

) ⊂ U

∪···∪U

Then

D = E.

Proof. Let D

be an open evolution with initial data U

and let D

be the open

evolution with initial data ∪

i=1

. Since the equation is orientation-free, we apply

the separation lemma (stated after this proof as Lemma 4.5.13) to obtain that

= ∪

i=1

190 Chapter 4. Classical level set metho d

By order preserving property (Theorem 4.5.2 (iv)) we see

E(t) ⊂ D

(t − t

α,

) ⊂∪

i=1

(t − t

α

) ⊂∪

i=1

(t − t

α,

)

for t>t

α,

. By continuity, letting  →∞yields

E(t) ⊂∪

i=1

(t)fort>0.

On the other hand

⊂ E

,whereE

is the closed evolution with initial data

.SinceU

↓ U

, by monotone convergence (Theorem 4.5.4) we have E

↓ E

where E

is the closed evolution with initial data U

Since E(t) ⊂∪

i=1

(t), letting α →∞,wegetE(t) ⊂∪

i=1

(t) for all

t>0. Since we have assumed E

= D

,weget

E(t) ⊂∪

i=1

(t)fort>0.

By the order preserving property, D

⊂ D for all i =1,...,k,sowenowobtain

E(t) ⊂

D(t) for all t ≥ 0, i.e., E ⊂ D.ThusD = E since D ⊂ E is trivial. 

()

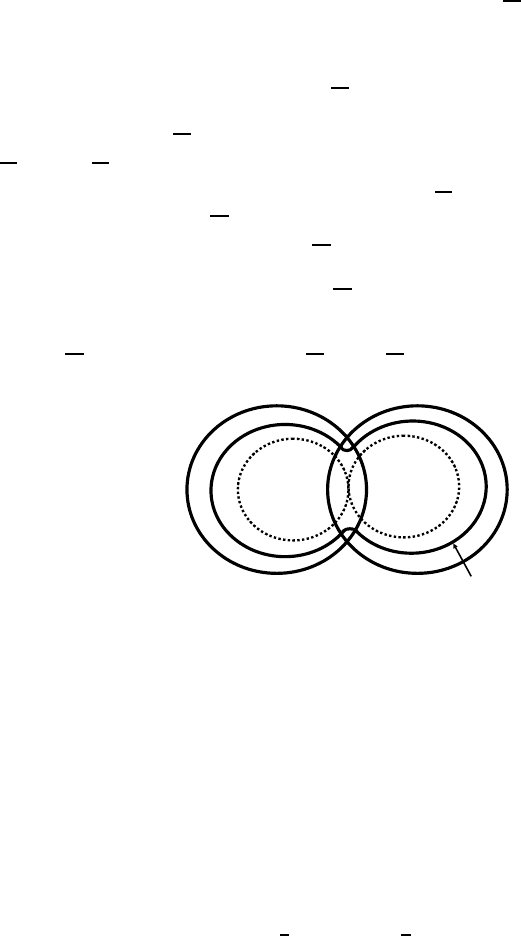
Figure 4.6: Regularity criterion

Lemma 4.5.13 (Separation). Assume (W) and (4.1.1) is orientation-free. Let D

be an open evolution (i =1, 2).

(i) If D

(0) and D

(0) are disjoint so are D

and D

(ii) Let D be the open evolution with initial data D

(0) ∪ D

(0).IfD

(0) and

(0) are disjoint then D = D

∪ D

Proof. (i) Let d(≥ 0) be the distance between D

(0) and D

(0) and let d

(x)

denote the distance from x ∈ R

to ∂(D

(0))(j =1, 2). Deﬁne

(x)=

⎧

⎨

⎩

(x)+d/2forx ∈ D

(0),

−d

(x) − d/2forx ∈ D

(0),

(x) ∧

) − (d

(x) ∧

)otherwise.

We claim that u

is Lipschitz with constant 1. In the open sets D

(0)(j =1, 2)

this is clear since the distance to a set is always Lipschitz with constant 1. Outside

4.5. Various properties of evolutions 191

of the closure of the D

(0) we always have d

(x)+d

(x) ≥ d, by the triangle

inequality. So the open sets

= {x ∈ R

\ (D

(0) ∪ D

(0)); d

(x) <d/2}

are disjoint. On these sets u

(x)=±(d

(x)− d/2) so that u

is also Lipschitz with

constant 1 on these sets. Finally u

(x) vanishes outside D

(0) ∪ D

(0) ∪ V

∪ V

Collecting these separate Lipschitz estimates we ﬁnd that u

is Lipschitz with

constant 1 in R

Since u

is Lipschitz, there is a unique solution u of (4.1.2) which is uniformly

continuous in R

× [0,T



] for every T



<T.Since±u − c(c ∈ R) is also a solution

of (4.1.2) by invariance and the orientation-free property,

= {(x, t) ∈ [0,T



) × R

; u(x, t) >d/2},

= {(x, τ) ∈ [0,T



) × R

; u(x, t) < −d/2}

are open evolutions with initial data D

(0) and D

(0). Clearly D

and D

are

disjoint. Since u is uniformly continuous, the distance of D

(t),D

(t) is uniformly

positive for all t ∈ [0,T



]ifd>0. This property will be used in the proof of (ii).

(ii) There are sequences of open sets D

↑ D

(0)(i =1, 2) such that the distance

from D

to ∂(D

(0)) is positive. Let u

be the solution of (4.1.2) such that u

t=0

is uniformly continuous and that u

(x) > 0forx ∈ D

and u

(x)=0for

x/∈ D

. The open evolution D

with initial data D

is given by

= {(x, t); u

(x, t) > 0}

and u

≥ 0 everywhere. Since the distance between D

and D

is positive, the

distance between D

is positive in R

× [0,T



]. Thus u

∨ u

is also a solution

of (4.1.2) so the open evolution D

with initial data D

∪ D

equals D

∪ D

By monotone convergence we see D

↑ D and D

↑ D

.ThusD = D

∪ D

. 

Remark 4.5.14. (i) If we consider only bounded evolutions D and E in the

sense that D(0) and E(0) are bounded, we may replace (CP) by (BCP) in the

assumption (W). By Remark 4.3.7 the requirement of (4.3.1) is unnecessary since

(4.3.5) is always fulﬁlled.

(ii) The order preserving property of Theorem 4.5.2 can be strengthened by in-

troducing super level sets of sub- and supersolutions instead of solutions. We just

give below a typical result corresponding to Theorem 4.5.2 (i) when D and D



are

bounded. Assume that bounded open sets D and D



in Z = R

× [0,T)aresuper

level sets of the form

D = {(x, t) ∈ Z; u(x, t) > 0},



= {(x, t) ∈ Z; v(x, t) > 0}

(4.5.2)

for some subsolution u and supersolution v of (4.1.2) and (4.1.3) such that u and

v are continuous in Z and u|

t=0

, v|

t=0

∈ K

)forsomeα<0. If (BCP) holds,

192 Chapter 4. Classical level set metho d

then D ⊂ D



holds provided that D(0) ⊂ D



(0). This is easy to prove by (BCP)

since we may assume that u ≤ v at t = 0 by the invariance Theorem 4.2.1 and

Lemma 4.2.9.

We are tempted to introduce a notion of subsolution for sets D if it is of the

form (4.5.2). However, this notion is not the same as the notion of set-theoretic

subsolution deﬁned in Deﬁnition 5.1.1. It agrees with the level set subsolution in

Deﬁnition 5.2.2 as proved in Proposition 5.2.3. The diﬀerence of these two notions

stems from fattening phenomena, as explained in Chapter 5.

4.6 Convergence properties for level set equations

We shall study whether solutions of approximate equation

V = f

(z,n, ∇n)(4.6.1)

converges to the solution of

V = f (z,n, ∇n)(4.6.2)

when f

tends to f as ε → 0 in a certain sense. We ﬁrst discuss convergence of

solutions of level set equations.

Theorem 4.6.1 (Convergence). Assume that F

, F : R

× [0,T] × (R

\{0}) ×

→ R (0 <T <∞, 0 <ε<1) are continuous and geometric. Assume that

there is c ∈ C(0,r

) that satisﬁes (4.3.1). Assume that there is a constant C such

that

(x, t, p, ±I)|≤C|F (x, t, p, ±I)|

for (x, t, p) ∈ R

× [0,T] × (B

(0) \{0})

(4.6.3)

for some r

∈ (0,r

). Assume that F

→ F locally uniformly in R

× [0,T] ×

\{0}) × S

. Assume that u

0ε

∈ BUC(R

) converges to u

∈ BUC(R

)

uniformly in R

as ε → 0.Letu

∈ BUC(R

× [0,T)) be the F

N -solution of

+ F

(z,∇u, ∇

u)=0 (4.6.4)

with initial data u

0ε

.Thenlim

ε→0

= u ∈ BUC(R

× [0,T)) exists and u is the

(F )-solution of the limit equation

+ F (z,∇u, ∇

u)=0 (4.6.5)

with initial data u

provided that (4.6.4), (4.6.5) satisﬁes (CP) with Ω=R

Moreover, the convergence is locally uniform in R

× [0,T).

Proof. By (4.6.3) and (3.1.2) we see that F

) ⊃F

(F ) and (2.2.4) is ful-

ﬁlled. (The existence of c guarantees that F

N (F) = ∅ by Lemma 3.1.3.) We now

apply the stability results (Theorem 2.2.1) and observe that

u = lim sup

∗

and u = lim inf

∗

4.6. Convergence prop erties for level set equations 193

are F

(F )-sub- and supersolutions of (4.2.1) provided that u<∞ and u > −∞.

We shall prove that

u<∞ and lim

t↓0

sup

(u(ξ,t) − u

(ξ)) ≤ 0.

Since u

converges to u

uniformly in R

and u

, u

∈ BUC(R

), there is a

modulus of continuity independent of ε ∈ (0, 1) such that

(x) − u

(ξ) ≤ ω(|x − ξ|),ε∈ (0, 1),x∈ R

By the assumptions (4.3.1) and (4.6.3) there is h ∈F

N (F) ⊂F

N (F

) such that

sup h



< ∞.Moreover,

:= sup

0≤t<T

sup

x,p∈R

|F (x, t, ∇

(h(ρ)), ±∇

h(ρ))| < ∞, (ρ = |ρ|)(4.6.6)

is bounded for ε ∈ (0, 1), i.e.,

B =sup

0<ε<1

< ∞. (4.6.7)

For each δ>0thereisA

> 0 such that ω(s) ≤ δ + A

, s ≥ 0. Thus

(x) ≤ u

(ξ)+δ + A

h(|x − ξ|).

Since B is independent of ε, by Lemma 4.3.3 and its proof the function V

(x)=

h(|x|)+M

t is an F

N (F

)-supersolution of (4.6.4) (independent of ε). So the

function

(x, t)=u

(ξ)+δ + V

(x − ξ, t)

is also an F

N (F

)-supersolution of (4.6.4). Since u

and w

is uniformly continu-

ous on R

×[0,T), by (CP) we have u

≤ w

.Inparticular,u<∞ on R

×[0,T).

Since u

≤ w

,wesee

u(ξ, t) ≤ lim

ε→0

(ξ)+δ + Mt.

Thus

lim

t↓0

sup

ξ∈R

(u(ξ,t) − u

(ξ)) ≤ δ.

Since δ>0 is arbitrary, we get

lim

t↓0

sup

ξ∈R

(u(ξ,t) − u

(ξ)) ≤ 0.

A symmetric argument yields u

> −∞ and

lim

t↓0

sup

ξ∈R

(ξ) − u(ξ, t)) ≤ 0.

194 Chapter 4. Classical level set metho d

In particular

t=0

= u|

t=0

= u

.Sinceu

is uniformly continuous, these two

inequalities yield

sup

0≤t,s≤ε

sup

|ξ−η|≤ε

(u(ξ,t) − u(ξ, s)) → 0asε → 0.

We are now in position to apply (CP) to get

u ≤ u. The converse inequality is

trivial so

u = u. By deﬁnition of lim sup

∗

, lim inf

∗

this implies that u

converges

to u locally uniformly in R

× [0,T)asε → 0. Moreover u|

t=0

= u

and u solves

(4.6.5) since u = u

= u is both F

N (F)-sub- and supersolution. 

Remark 4.6.2. (i) We may replace (4.6.3) by F

N (F) ⊂F

N (F

)inTheorem

4.6.1. If f

and f are independent of x, t in (4.6.1), (4.6.2) and

(p, Q

(X))|≤A(1 + |Q

(X)|),ε∈ (0, 1)

with constant A>0, then F(F

)=F(F

)(={h ∈ C

(R); h(0) = h



(0) =



(0) = 0, h



(σ) > 0forσ>0}). So in this situation we have convergence of

solutions of level set equations.

(ii) If we fully use (3.1.5) for

u and u, we can also prove that u

→ u uniformly in

× [0,T



]forT



<T.

(iii) If u

∈ K

)andspt(u

− α

) ⊂ int B

for some R independent of

ε ∈ (0, 1), then there is R



≥ R (independent of ε)thatsatisﬁes

spt(u

− α

) ⊂ intB



× [0,T).

(In particular, the convergence u

→ u is uniform in R

× [0,T



], T



<T.) This

uniform estimate of the support u

− α

can be proved by constructing a suitable

super- and subsolution as in the proof of Theorem 4.3.1. Instead of w

we use

here

(x, t)=max{ v

(x, t)+σ, α

where σ is chosen such that u

(x) ≤ σ − h(|x|)forx satisfying u

(x) = α

.We

estimate w

−

≤ u

≤ w

by constructing w

−

similarly and observe that u

− α

outside Ω



× [0,T), where Ω



is some ball.

(iv) Geometricity of F

and F is not necessary if there exists V

(independent of ε)

in the proof of Theorem 4.6.1 and if assumptions in Theorem 2.2.1 are fulﬁlled. We

give another version of convergence results whose proof parallels that of Theorem

4.6.1.

Theorem 4.6.3 (Convergence without geometricity). Assume that F , F

: R

[0,T]×(R

\{0})×S

→ R (0 <T <∞, 0 <ε<1) are continuous. Assume that

(F ) ⊂F

) and fulﬁlls (2.2.4). Assume that B in (4.6.6), (4.6.7) is ﬁnite

for some h ∈F

N (F). Assume that F

→ F locally uniformly in R

× [0,T] ×

\{0}) × S

. Assume that u

0ε

∈ BUC(R

) converges to u

∈ BUC(R

)

uniformly in R

as ε → 0.Letu

∈ BUC(Z) be the F

)-solution of (4.6.4)

4.6. Convergence prop erties for level set equations 195

with initial data u

0ε

.Thenlim

ε→0

= u ∈ BUC(Z) exists and u is the F

(F )-

solution of (4.6.5) with initial data u

provided that (4.6.4), (4.6.5) satisﬁes (CP)

with Ω=R

. Moreover the convergence is locally uniform in Z = R

× [0,T).

We take this opportunity to prove Lemma 4.2.12. We suppress the symbol

N in the proof.

Proof of Lemma 4.2.12. Since u

∈ BUC(R

) and the solution u

with initial

data u

also belongs to BUC(Z), we see (CP) is applicable to conclude u

≤

m+1

(≤ u)inZ = R

× [0,T). We set

v(z)= sup

m≥1

(z)(= lim

m→∞

(z)),z∈ Z.

Since u

is continuous, v is lower semicontinuous in Z.Thus

v(z) = lim

r↓0

inf{v(ζ); ζ ∈ Z, |ζ − z|≤r}

≥ lim

r↓0

inf{u

(ζ); ζ ∈ Z, |ζ − z|≤r, k ≥

}

≥ lim inf{u

(ζ); ζ ∈ Z, |ζ − z|≤r},m=1, 2,....

The last quantity equals u

(z) so sending m →∞yields

v(z) ≥ lim

r↓0

inf{u

(ζ); ζ ∈ Z; |ζ − z|≤r, k ≥

}≥v(z).

Thus we conclude

v(z) = (lim inf

m→∞

∗

)(z).

By the stability (Theorem 2.2.1) v is a supersolution of (4.2.1).

We shall prove that

lim

r↓0

sup{u(x, t) − v(y, s); |x − y|≤r, t ∨ s ≤ r}≤0.

Let h ∈F

N with sup h



< ∞. As in the proof of Lemma 4.3.4 for each δ>0

there are positive constants A

and M

= M

such that

(x, t)=u

(ξ) − δ − A

h(|x − ξ|) − M

is a subsolution of (4.2.1) in R

× (0,T)and

(x) − δ ≥ w

(x, 0).

By Dini’s theorem u

→ u

locally uniformly in R

.Since{u

} is bounded

from below, there is  = (δ, ξ) such that

≥ w

(·, 0) in R

for m ≥ .

196 Chapter 4. Classical level set metho d

Since both w

and u

are uniformly continuous in R

×[0,T



], T



<T, we see, by

(CP), that u

≥ w

for all m ≥ . This yields v ≥ w

in R

× [0,T)forδ ∈ (0, 1),

ξ ∈ R

.Inparticular,v(y, s) ≥ w

(y,s). Thus

u(x, t) − v(y, s) ≤ u(x, t) − w

(y,s) ≤ u(x, t) − u

(y)+δ + M

Since u is uniformly continuous in Z, it is clear that

lim

r↓0

sup{u(x, t) − u

(y); |x − y|≤r, t ≤ r}≤0.

We thus obtain that

lim

r↓0

sup{u(x, t) − v(y, s); |x − y|≤r, t ∨ s ≤ r}≤δ.

Since δ>0 is arbitrary, we conclude

lim

r↓0

sup{u(x, t) − v(y, s); |x − y|≤r, t ∨ s ≤ r}≤0

and apply (CP) to get u ≤ v in Z.Sincev ≤ u, this implies u ≡ v.Thuswehave

proved that u

↑ u. 

The convergence result (Theorem 4.6.1) yields the convergence of evolutions

of (4.6.1) to (4.6.2) provided that fattening does not occur.

Theorem 4.6.4 (Convergence of evolutions). Assume that (4.6.1) and (4.6.2)

fulﬁll (W). Assume that f

converges to f as ε → 0 locally uniformly on R

[0,T]×E. Assume that F

and F

satisfy F

N (F

) ⊂F

N (F

) for ε ∈ (0, 1).Let

and E

be compact sets in R

.LetE

and E be a closed evolution of (4.6.1)

and (4.6.2) with initial data E

and E

, respectively. Assume that d

) → 0

as ε → 0. Assume that int E is regular. Then

(i) d



,E) → 0 as ε → 0,whered



denotes the Hausdorﬀ distance in R

[0,T



], T



<T.

(ii) Assume that E is strongly regular in the sense that E(t)=

D(t) for all

t ∈ [0,T



] where D is the open evolution of (4.6.1) with initial data int E

Then d

(t),E(t)) → 0 as ε → 0 and the convergence is uniform in

t ∈ [0,T



For the proof we need a lemma on level sets.

Lemma 4.6.5. Let Z and Y be compact metric spaces. Assume that f

∈ C(Z)

converges to f

∈ C(Z) as ε → 0 uniformly in λ ∈ Y ,whereε ∈ (0, 1).Fora

given  ∈ R assume that {z ∈ Z; f

(z) ≥ } := {f

≥ } = {f

>}. Assume that

the sets {f

≥ } and {f

≥ } are compact in Z for all λ ∈ Y . Assume that for

small ε>0 the set {f

≥ } is continuous in λ ∈ Y with respect to the Hausdorﬀ

metric d

in Z.Thend

({f

≥ }, {f

≥ }) → 0 as ε → 0 uniformly in λ ∈ Y .

4.6. Convergence prop erties for level set equations 197

Proof. We ﬁrst note that for each η>0thereisε

∈ (0, 1) such that {f

≥ }⊂

≥ }

for all ε ∈ (0,ε

), λ ∈ Y ,whereA

= {z ∈ Z;dist(z, A) ≤ η} for

a subset A of Z.Ifnot,forsomeη>0thereisasequenceε

→ 0, {λ

}⊂Y ,

}⊂Z that satisﬁes dist (z

, {f

≥ }) >ηand z

∈{f

≥ }. We may assume

that λ

→ λ

, z

→ z

as j →∞by taking a subsequence. Since f

converges to

uniformly in Z and for λ ∈ Y ,wehavef

) → f

). Since f

) ≥ ,

this implies f

) ≥ . This is absurd since dist (z

, {f

≥ }) = lim

j→∞

dist

, {f

≥ }) ≥ η by continuity of {f

≥ } in λ ∈ Y .Thus,{f

≥ }⊂{f

≥ }

for small ε>0 uniformly in λ ∈ Y .

It remains to prove that {f

≥ }⊂{f

≥ }

for suﬃciently small ε

(uniformly in λ ∈ Y ). If not, there is r>0andλ

with z

∈{f

≥ }

such that {f

≥ }∩B

)=∅ for some sequence ε

→ 0. By continuity of

≥ } in λ we may assume that λ

→ λ

and z

→ z

∈{f

≥ } so that

≥ }∩B

r/2

)=∅.Sincef

→ f

uniformly in Z and for λ ∈ Y , this implies

that f

≤  on B

r/2

). This contradicts {f

>} = {f

≥ }. 

Lemma 4.6.6 (Strongly regular evolution). Assume (W). Assume that E

= E(0)

is compact. If E is strongly regular, then t → E(t) is continuous as a set-valued

function on [0,T).

Proof. Since t → E(t) is left continuous and upper semicontinuous, it suﬃces to

prove that E(t) is right lower semicontinuous in t.

Assume that E(t) is not right continuous at some point t

∈ [0,T). Then

there is a point x

∈ E(t

)andaballB

) such that E(t

) ∩ B

)=∅ for

some t

↓ t

.SinceD(t

)=E(t

)thereisaballB ⊂ D(t

) ∩ E(t

). Comparing

a special subsolution we conclude that an open evolution starting with intB at

t = t

contains a center of B for [t

+ δ)forsomeδ>0. Thus by comparison

we see D(t

) ∩ B

) = ∅ which contradicts E(t

) ∩ B

)=∅. Therefore E(t)

is right continuous on [0,T). 

Proof of Theorem 4.6.4. For E

we set

(x)=(sd(x, ∂E

) ∧ 1) ∨ (−1).

Since d

) → 0asε → 0, we see that u

converges to

(x)=(sd(x, ∂E) ∧ 1) ∨ (−1).

Let u

be the solution of (4.6.4) with u

t=0

= u

and let u be the solution of (4.6.5)

with u|

t=0

= u

. Our assumption f

→ f guarantees the convergence F

→ F

Theorem 4.6.1. By the convergence result (Theorem 4.6.1 and Remark 4.6.2 (i))

converges to u uniformly in R

×[0,T



] for every T



< ∞.SinceE

= {u

≥ 0},

E = {u ≥ 0}, we apply Lemma 4.6.5 with Z = B

× [0,T



]sothat{u

≥ 0}⊂Z

and Y = ∅ and f

= u

to get (i). To show (ii) it suﬃces to take Z = B

Y =[0,T



]andf

= u

(,λ), since the strong regularity implies the continuity of

E(t) by Lemma 4.6.6. 