Gebali F. Analysis Of Computer And Communication Networks

Подождите немного. Документ загружается.

Problems 45

1.28 A router has ten input ports and at a given time instance each input could

receive a packet with probability a or it could be idle (with probability b =

1 −a). Let the random variable X denote the number of active input ports.

(a) List all possible outcomes of the experiment.

(b) Find the value of X for each outcome.

(d) Sketch the cdf for this random variable.

1.29 Sketch the pdf associated with the random variable in Problem 1.28.

1.30 A traffic source generates a packet at a certain time step with probability a.

Let the random variable X denote the number of packets produced in a period

T = 5 time steps.

(a) List all possible outcomes of the experiment.

(b) Find the value of X for each outcome.

(d) Sketch the cdf for this random variable assuming a = 0.2.

The Probability Density Function (pdf)

1.31 Sketch the pdf and cdf for the binomial distribution. Assume a = 0.3 and

N = 5.

1.32 Sketch the pdf associated with the random variable in Problem 1.19.

1.33 Sketch the pdf associated with the random variable in Problem 1.23.

1.34 Sketch the pdf associated with the random variable in Problem 1.24.

1.35 Sketch the pdf associated with the random variable in Problem 1.26.

Expected Value

1.36 Prove that (1.34) on page 15 converges to (1.33) as n →∞. Start your analysis

by (a) assuming that n samples are grouped such that n

samples produce

the same outcome. (b) Use the definition of probability in (1.6) on page 8 to

complete your proof.

1.37 What are the expected values for the random variables ⌰ and Q in Example

1.14?

1.38 Assume a Poisson process, rate parameter is λ, that gives rise to two random

variables X

and X

which correspond to k packets received at times t

and

, respectively where t

≥ t

. (a) Find the mean and variance for these two

random variables. (b) Now define a new random variable Y = X

− X

and

find its mean and variance.

1.39 Find the expected value for the random variable in Problem 1.19.

1.40 Find the expected value for the random variable in Problem 1.23.

1.41 Find the expected value for the random variable in Problem 1.24.

46 1 Probability

1.42 Find the expected value for the random variable in Problem 1.26.

1.43 Repeat Example 1.16 when the random variable E is treated as a discrete

random variable.

The Uniform Distribution

1.44 Write down the pdf and cdf for the uniform distribution of a continuous ran-

dom variable X that spans the range a ≤ x < b.

1.45 Repeat the above problem when the random variable is discrete and has n

discrete values in the same range given above.

1.46 Find the average value and variance for the random variable in Problem 1.44.

1.47 Find the average value and variance for the random variable in Problem 1.45.

The Binomial Distribution

1.48 Prove that the mean and standard deviation of the binomial distribution are

Na and

√

a(1 −a), respectively.

1.49 Sketch the pdf for the binomial distribution. Assume values for a and N.

1.50 The probability of error in a single packet is 10

−5

. What is the probability that

three errors occur in 1,000 packets assuming binomial distribution.

1.51 Assume q as the probability that people making reservations on a certain flight

will not show up. The airline then sells t tickets for a flight that takes only s

passengers (t > s). Write an expression for the probability that there will be a

seat available for every passenger that shows up. What is that probability for

the special case when only one seat is oversold (i.e., t = s +1)?

The Poisson Distribution

1.52 Verify that the mean and standard deviation for the binomial and Poisson dis-

tributions become almost identical for large N and small p as was discussed

in Section 1.26.

1.53 The probability of a defective electronic component is 0.1. Find the follow-

ing.

(a) The mean and standard deviation for the distribution of defective com-

ponents in a batch of 500 components using the Poisson and binomial

distributions.

(b) The probability that 2 components are defective in a batch of 500 compo-

nents.

1.54 Sketch the pdf for the Poisson distribution for different values of λt and k.

Comment on your results.

1.55 Sketch on one graph the binomial and Poisson distributions for the case N = 5

and p = 0.1. Assume λt = 0.5.

Problems 47

1.56 Repeat question 1.50 assuming Poisson distribution with λt = 0.1, where

we assumed the “rate” λ of occurrence of error per packet is 10

−4

and the

“duration” of interest is t = 1000 packets.

1.57 Five percent of the rented videos are worth watching. Find the probability that

in a sample of 10 videos chosen at random, exactly two will be worth watching

using

(a) binomial distribution and

(b) Poisson distribution.

The Exponential Distribution

1.58 Derive the cdf for the exponential distribution.

1.59 Prove that the Pareto distribution formula given by (1.49) is a valid pdf (i.e.,

the area under the curve is 1).

Joint pmf

1.60 Consider the random experiment of throwing a dart at a target. The point of

impact is characterized by two random variables X and Y to indicate the lo-

cation of the dart assuming the center is the point of origin. We can justifiably

assume that X and Y are statistically independent.

(a) Write down the joint cdf F

(x, y) as a function of the individual cdfs

(x) and F

(y).

(b) Write down the joint pdf f

(x, y) as a function of the individual pdfs

(x) and f

(y).

(x) and f

(y) assuming that each follows

the normal (Gaussian) distribution.

1.61 Find the correlation between the two random variables X and Y in Example

1.22 on page 32.

1.62 Find the variance of random variable X in Example 1.22 on page 32.

1.63 Find the covariance between the two random variables X and Y in Example

1.22 on page 32.

1.64 Prove (1.110) on page 34.

1.65 Find the correlation coefficient for the two random variables X and Y in

Example 1.22 on page 32.

Random Numbers

1.66 Use the inversion method to generate y in the range 1–5 such that the target

pdf is f

(

)

∝ 1/

√

1.67 Generate the random number y that has pdf f (y) = (1 + y)/

√

y using the

importance sampling method.

48 1 Probability

References

1. P.Z. Peebles, Probability, Random Variables, and Random Signal Principles, McGraw–Hill,

New York, 1993.

2. A. Papoulis, Probability, Random Variables, and Stochastic Processes, McGraw-Hill,

New York, 1984.

3. G.R. Cooper and C.D. McGillem, Probability Methods of Signal and System Analysis, Oxford

University Press, New York, 1999.

4. “statistics” Encyclopedia Britannica Online. http://search.eb.com/bol/topic?eu=115242&

sctn=8

5. R.D. Yates and D.J. Goodman, Probability and Stochastic Processes, John Wiley, New York,

1999.

6. A. Erramilli, G. Gordon, and W. Willinger, “Applications of fractals in engineering for realistic

traffic processes”, International Teletraffic Conference, Vol. 14, pp. 35–44, 1994.

7. W. Leland, M. Taqqu, W. Willinger, and D. Wilson, “On the self-similar nature of Ethernet

traffic”, IEEE/ACM Transactions on Networking, vol. 2, pp. 1–15, 1994.

8. W. Willinger, M. Taqqu, R. Sherman, and D. Wilson, “Self-similarity through high variability

statistical analysis of Ethernet LAN traffic at the source level”, IEEE/ACM Transactions on

Networking, vol. 2, 1997.

9. T. Hettmansperger and M. Keenan,“Tailweight, statistical interference and families of distri-

butions – A brief survey” in Statistical Distributions in Scientific Work, vol. 1, G.P. Patil et al.

ed., Kluwer, Boston, 1980.

10. R. Syski, Random Processes: A First Look, Marcel Dekker, New York, 1979.

11. W.H. Press, S.T. Teukolsky, W.T. Vetterling, and B.P. Fhannery, Numerical Recipes in C: The

Art of Scientific Computing, Cambridge University Press, Cambridge, 1992.

Chapter 2

Random Processes

2.1 Introduction

We saw in Section 1.11 on page 10 that many systems are best studied using the

concept of random variables where the outcome of a random experiment was associ-

ated with some numerical value. Next, we saw in Section 1.27 on page 30 that many

more systems are best studied using the the concept of multiple random variables

where the outcome of a random experiment was associated with multiple numerical

values. Here we study random processes where the outcome of a random experiment

is associated with a function of time [1]. Random processes are also called stochastic

processes. For example, we might study the output of a digital filter being fed by

some random signal. In that case, the filter output is described by observing the

output waveform at random times.

Thus a random process assigns a random function of time as the outcome of a

random experiment. Figure 2.1 graphically shows the sequence of events leading to

assigning a function of time to the outcome of a random experiment. First we run

the experiment, then we observe the resulting outcome. Each outcome is associated

with a time function x(t).

A random process X(t) is described by

• the sample space S which includes all possible outcomes s of a random experi-

ment

• the sample function x(t) which is the time function associated with an outcome

s. The values of the sample function could be discrete or continuous

• the ensemble which is the set of all possible time functions produced by the ran-

dom experiment

• the time parameter t which could be continuous or discrete

• the statistical dependencies among the random processes X(t) when t is changed.

Based on the above descriptions, we could have four different types of random

processes:

1. Discrete time, discrete value: We measure time at discrete values t = nT with

n = 0, 1, 2, .... As an example, at each value of n we could observe the number

of cars on the road x(n). In that case, x(n) is an integer between 0 and 10, say.

F. Gebali, Analysis of Computer and Communication Networks,

DOI: 10.1007/978-0-387-74437-7



Springer Science+Business Media, LLC 2008

50 2 Random Processes

Random

experiment

Random

outcome

Corresponding

function of

time: x(t)

Mapping

function

Fig. 2.1 The sequence of events leading to assigning a time function x(t) to the outcome of a

random experiment

Each time we perform this experiment, we would get a totally different sequence

for x(n).

2. Discrete time, continuous value: We measure time at discrete values t = nT with

n = 0, 1, 2, .... As an example, at each value of n we measure the outside tem-

perature x(n). In that case, x(n) is a real number between −30

◦

and +45

◦

,say.

Each time we perform this experiment, we would get a totally different sequence

for x(n).

3. Continuous time, discrete value: We measure time as a continuous variable t.As

an example, at each value of t we store an 8-bit digitized version of a recorded

voice waveform x(t). In that case, x(t) is a binary number between 0 and 255,

say. Each time we perform this experiment, we would get a totally different se-

quence for x(t).

4. Continuous time, continuous value: We measure time as a continuous variable

t. As an example, at each value of t we record a voice waveform x(t). In that

case, x(t) is a real number between 0 V and 5 V, say. Each time we perform this

experiment, we would get a totally different sequence for x(t).

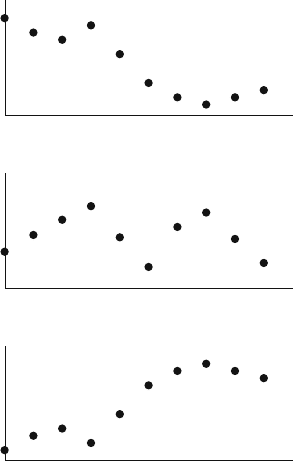
Figure 2.2 shows a discrete time, discrete value random process for an observa-

tion of 10 samples where only three random functions are generated. We find that

for n = 2, the values of the functions correspond to the random variable X(2).

Therefore, random processes give rise to random variables when the time value t

or n is fixed. This is equivalent to sampling all the random functions at the specified

time value, which is equivalent to taking a vertical slice from all the functions shown

in Fig. 2.2.

Example 2.1 A time function is generated by throwing a die in three consecutive

throws and observing the number on the top face after each throw. Classify this

random process and estimate how many sample functions are possible.

This is a discrete time, discrete value process. Each sample function will be have

three samples and each sample value will be from the set of integers 1 to 6. For

example, one sample function might be 4, 2, 5. Using the multiplication principle

for probability, the total number of possible outputs is 6

= 216.

2.2 Notation 51

0123456789

Fig. 2.2 An example of a discrete time, discrete value random process for an observation of 10

samples where only three random functions are possible.

2.2 Notation

We use the notation X(t) to denote a continuous-time random process and also to

denote the random variable measured at time t. When X(t) is continuous, it will

have a pdf f

(x) such that the probability that x ≤ X ≤ x + ε is given by

p(X = x) = f

(x) dx (2.1)

When X(t) is discrete, it will have a pmf p

(x) such that the probability that

X = x is given by

p(X = x) = p

(x) (2.2)

Likewise, we use the notation X(n) to denote a discrete-time random process

and also to denote the random variable measured at time n. That random variable is

statistically described by a pdf f

(x) when it is continuous, or it is described by a

pmf p

(x) when it is discrete.

52 2 Random Processes

2.3 Poisson Process

We shall encounter Poisson processes when we describe communication traffic. A

Poisson process is a stochastic process in which the number of events occurring in a

given period of time depends only on the length of the time period [2]. This number

of events k is represented as a random variable K that has a Poisson distribution

given by

p(k) =

(λ t)

−λ t

(2.3)

where λ>0 is a constant representing the rate of arrival of the events and t is the

length of observation time.

2.4 Exponential Process

The exponential process is related to the Poisson process. The exponential process

is used to model the interarrival time between occurrence of random events. Exam-

ples that lead to an interarrival time include the time between bus arrivals at a bus

stop, the time between failures of a certain component, and the time between packet

arrival at the input of a router.

The random variable T could be used to describe the interarrival time. The prob-

ability that the interarrival time lies in the range t ≤ T ≤ t + dt is given by

λe

−λ t

dt (2.4)

where λ is the average rate of the event under consideration.

2.5 Deterministic and Nondeterministic Processes

A deterministic process is one where future values of the sample function are known

if the present value is known. An example of a deterministic process is the modula-

tion technique known as quadrature amplitude modulation (QAM) for transmitting

groups of binary data. The transmitted analog waveform is given by

v(t) = a cos(ωt + φ) (2.5)

where the signal amplitude a and phase angle φ change their value depending on

the bit pattern that has been received. The analog signal is transmitted for the time

period 0 ≤ t < T

. Since the arriving bit pattern is random, the values of the

corresponding two parameters a and φ are random. However, once a and φ are

determined, we would be able to predict the shape of the resulting waveform.

2.6 Ensemble Average 53

A nondeterministic random process is one where future values of the sample

function cannot be known if the present value is known. An example of a nondeter-

ministic random process is counting the number of packets that arrive at the input

of a switch every one second and this observation is repeated for a certain time.

We would not be able to predict the pattern even if we know the present number of

arriving packets.

2.6 Ensemble Average

The random variable X

(

)

represents all the possible values x obtained when time

is frozen at the value n

. In a sense, we are sampling the ensemble of random func-

tions at this time value.

The expected value of X

(

)

is called the ensemble average or statistical average

(

)

of the random process at n

. The ensemble average is expressed as

(t) = E[X(t)] continuous-time process (2.6)

(n) = E[X(n)] discrete-time process (2.7)

The ensemble average could itself be another random variable since its value

could change at random with our choice of the time value t or n.

Example 2.2 The modulation scheme known as frequency-shift keying (FSK) can

be modeled as a random process described by

X(t) = a cos ωt

where a is a constant and ω corresponds to the random variable ⍀ that can have

one of two possible values ω

and ω

that correspond to the input bit being 0 or 1,

respectively. Assuming that the two frequencies are equally likely, find the expected

value μ(t) of this process.

Our random variable ⍀ is discrete with probability 0.5 when ⍀ = ω

or ⍀ = ω

The expected value for X(t) is given by

[

X(t)

]

= 0.5 a cos ω

t +0.5 a cos ω

= a cos



(

+ω

)



×cos



(

−ω

)



Example 2.3 The modulation scheme known as pulse amplitude modulation (PAM)

can be modeled as a random process described by

54 2 Random Processes

X(n) =

∞



i=0

g(n) δ(n − i)

where g(n) is the amplitude of the input signal at time n. g(n) corresponds to the

random variable G that is uniformly distributed in the range 0–A. Find the expected

value μ(t) of this process.

This is a discrete time, continuous value random process. Our random variable

G is continuous and the expected value for X(n) is given by

[

X(n)

]



gdg

2.7 Time Average

Figure 2.2 helps us find the time average of the random process. The time average

is obtained by finding the average value for one sample function such as X

(n)in

the figure. The time average is expressed as

X =



X(t) dt continuous-time process (2.8)

X =



N−1

X(n)] discrete-time process (2.9)

In either case we assumed we sampled the function for a period T or we observed

N samples. The time average

X could itself be a random variable since its value

could change with our choice of the random function under consideration.

2.8 Autocorrelation Function

Assume a discrete-time random process X(n) which produces two random vari-

ables X

= X

(

)

and X

= X

(

)

at times n

and n

respectively. The au-

tocorrelation function for these two random variables is defined by the following

equation:

(

, n

)

= E

[

]

(2.10)