Gebali F. Analysis Of Computer And Communication Networks

Подождите немного. Документ загружается.

1.15 Expected Value and Variance 15

The expectation is sometimes referred to as the first moment of the random vari-

able. Sometimes μ is used as another symbol for the expected value.

μ = E[X]

The mean (m) of a set of random variable samples is defined as

m =



i=1

(1.34)

The mean is not exactly equal to the expected value μ since m changes its value

depending on how many samples we take. However, as n →∞, the two quantities

become equal [5]. Higher moments are also useful and we define the variance,or

second central moment, of the random variable as

= E



(X −μ)



(1.35)

The variance describes how much of the mass of the distribution is close to the

expected value. A small value for σ

indicates that most of the random variable

values lie close to the expected value μ. In other words, small variance means that

the pdf is large only in regions close to the expected value μ. For an archery target

practice experiment, this might mean that most of the arrows were clustered together

and landed very close at some spot on the target (not necessarily dead center).

Conversely, a large variance means that the pdf is large for values of X far away

from μ. Again for the archery experiment, this means that most of the arrows were

not clustered together and landed at different spots on the target. The standard devi-

ation σ is simply the square root of the variance.

Example 1.15 Assume a random variable A from a binary random experiment in

which only two events result. A has two values a and 0. The probability that the

value a is obtained is p and the probability that the value 0 is obtained is q = 1 − p.

Find the expected value of A.

This is a discrete random variable and the pmf for A is

p(a) =



q when A = 0

p when A = a

(1.36)

The expected value is obtained from (1.33) as

E[A] = q ×0 + p ×a = pa (1.37)

Notice that the expected value will be between 0 and a since p is a nonnegative

fraction.

16 1 Probability

1.16 Common Continuous RVs

We discuss in the following sections some continuous random variables that are

useful for network simulations. Discussion of common discrete random variables is

found in later sections.

1.17 Continuous Uniform (Flat) RV

The uniform random variable, or uniform distribution, usually arises in physical

situations where there is no preferred value for the random variable. For example,

the value of a signal during analog-to-digital conversion could lie anywhere within

each quantization level. This distribution is also useful in our studies because it is

often used to obtain random numbers that obey the more sophisticated distributions

to be discussed below. These random numbers are then considered to be the “traffic”

generated at the inputs of our communication networks.

A uniform distribution is characterized by a random variable that spans in the

range a–b such that a < b,

f (x) =



1/(b −a) a ≤ x < b

0 otherwise

(1.38)

and the corresponding cdf is given by

F(x) =

⎧

⎨

⎩

0 x < a

(x −a)/(b − a) a ≤ x < b

1 x ≥ b

(1.39)

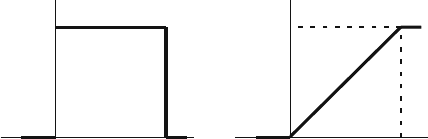
Typically a = 0 and b = 1. Figure 1.7(a) shows the pdf for the uniform distribu-

tion and Fig. 1.7(b) shows the corresponding cdf. The mean and variance for X are

given by

Fig. 1.7 The uniform

distribution for a continuous

random variable. (a) The pdf

and (b) is the corresponding

cdf

(x)

x01

(b)

(x)

x01

(a)

1.17 Continuous Uniform (Flat) RV 17

μ =

b +a

(1.40)

(b −a)

(1.41)

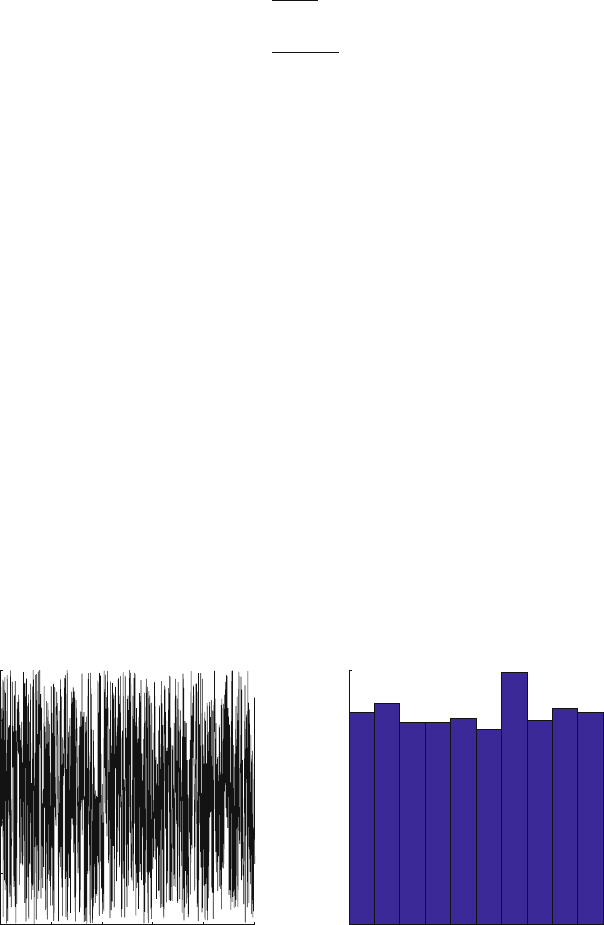
The following MATLAB code generates and plots a random variable having a

uniform distribution in the range 0 ≤ x < 1.

%uniform.m

n=1000 % number of samples is 1000

x=rand(1,n)

subplot(1,2,1)

plot(x,‘k’)

box off, axis square

xlabel(‘Sample index’), ylabel(‘Random number value’)

subplot(1,2,2)

hist(y)

title(‘pdf plot’)

box off, axis square

xlabel(‘Bins’), ylabel(‘Number of samples)

Figure 1.8 shows the result of running the code. Figure 1.8(a) shows the samples

and Figure 1.8(b) shows the histogram of the random variable. Notice that the distri-

bution of the samples in the different bins is almost equal. If we chose the number of

samples to be larger than 1000, the histogram would show more equal distribution

among the bins.

0 200 400 600 800 1000

0.2

0.4

0.6

0.8

Sample index

(a) (b)

Random number value

0 0.2 0.4 0.6 0.8 1

100

120

Bins

Bin count

Fig. 1.8 (a) One thousand samples of a random variable having the uniform distribution in the

range 0–1. (b) Histogram for the samples showing a uniform distribution

18 1 Probability

1.18 Gaussian RV

This distribution arises in many random variables used in electrical engineering such

as the noise in a wireless channel. The Gaussian distribution applies for the case of a

continuous random variable X that is allowed to have the values ranging from −∞

to +∞. The pdf for this distribution is given by

f (x) =

√

2π

−(x−μ)

/(2σ

)

(1.42)

where μ is the mean and σ is the standard deviation of the distribution. The cdf for

this distribution is given by

F(x) =



−∞

(

)

dy (1.43)

There is no closed-form formula for the cdf associated with the Gaussian distri-

bution but that function is tabulated in many textbooks on statistics. The standard

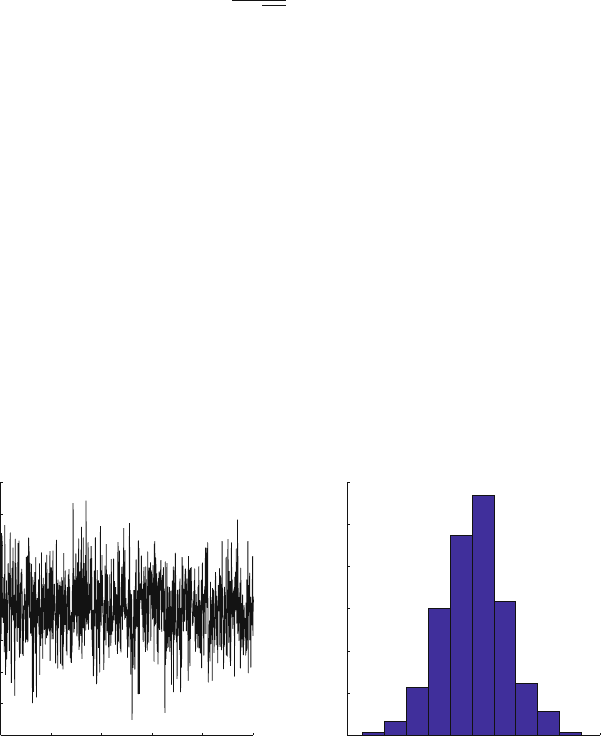
or normal random variable is a Gaussian RV with μ = 0 and σ = 1 [5]. Figure 1.9

shows the output of a Gaussian random variable with zero mean and unity variance

using the randn function of MATLAB. One thousand samples were generated in

this experiment.

0 200 400 600 800 1000

−4

−3

−2

−1

Sample index

(a) (b)

Random number value

−4 −2 0 2 4

100

150

200

250

300

Bins

Bin count

Fig. 1.9 Random numbers generated using the Gaussian distribution with zero mean and unity

variance. (a) shows the random samples and (b) shows their histogram

1.20 Pareto RV 19

1.19 Exponential RV

The exponential distribution applies for the case of a continuous random variable X

that is allowed to have the values ranging from 0 to +∞. The pdf for this distribution

is given by

f (x) = be

−bx

x ≥ 0 (1.44)

where b > 0. The corresponding cdf is given by

F(x) = 1 −e

−bx

(1.45)

The mean and variance for X are

μ =

(1.46)

(1.47)

A famous example of exponential RV is the radioactive decay where we have

f (t) = λe

−λt

t ≥ 0 (1.48)

Here λ is the rate of decay of an element. In that case 1/λ is called the lifetime when

the radioactive material decreases by the ratio 1/e.

1.20 Pareto RV

The Poisson and binomial distributions have been traditionally employed to model

traffic arrival at networks. Recent work has shown that such models may be in-

adequate because the traffic may exhibit periods of high data rates even when the

average data rate is low. This type of traffic is described as being self-similar (fractal)

[6–8]. Self-similar traffic has distributions with very high variance. Sometimes such

distributions are described as being heavy-tailed since the pdf has large values for x

far away from the mean μ. This type of distribution might then prove more accurate

in describing the pdf for the rate of data produced by a bursty source.

The Pareto distribution could be made to be a heavy-tailed distribution by proper

choice of its parameters. The Pareto distribution is described by the pdf

(

)

b+1

with a ≤ x < ∞ (1.49)

where a is the position parameter and b > 0 is the shape parameter. Figure 1.10

shows the pdf distribution for the case when a = 2 and b = 3 (solid line) and b = 5

20 1 Probability

Fig. 1.10 Pareto pdf

distribution for the case when

a = 2andb = 3(solid line)

and b = 5(dashed line)

2 2.5 3 3.5 4 4.5 5

–3

–2

–1

Pareto pdf

(dashed line). For the smaller value of shape parameter b, the pdf becomes flatter

and has higher values at larger values of x. This results in larger variance for X.The

corresponding cdf is

(

)

= 1 −





(1.50)

The mean and variance for X are

μ =

b −1

(1.51)

(

b −1

)

(

b −2

)

(1.52)

The mean is always positive as long as b > 1. The variance is meaningful only

when b > 2. From 1.50, we can write

p(X > x) = 1 − p(X ≤ x)





(1.53)

which means that the probability that the random variable has a value greater than

x decreases geometrically [9].

Pareto distribution is typically used to generate network traffic that shows bursty

behavior. This means that when a traffic burst is encountered, it is very probable that

the burst will continue. For such traffic, the shape parameter b is typically chosen in

the range 1.4–1.6.

1.22 Discrete Uniform RV 21

0 200 400 600 800 1000

Sample index

(a) (b)

Random number value

0 10 20 30

100

200

300

400

500

600

700

800

900

Bins

Bin count

Fig. 1.11 Random numbers generated using the Pareto distribution with a = 2andb = 2.5.

(a) shows the random samples and (b) shows their histogram

Figure 1.11 shows the output of a Pareto random variable with position parameter

a = 2 and shape parameter b = 2.5. One thousand samples were generated in this

experiment using the inversion method as described later in Section 1.35.2.

1.21 Common Discrete RVs

We discuss in the following sections some discrete random variables that are useful

for network simulations.

1.22 Discrete Uniform RV

Assume N is a random variable such that there are k distinct sample points. The

pmf for the discrete uniform RV is defined by

p(n) =

⎧

⎨

⎩

1/k 1 ≤ n ≤ k

0 otherwise

where n is the sample index. Alternatively, the pmf can be expressed in the form

p(n) =



i=1

δ(n − i) (1.54)

where δ( j) is the Dirac delta function which is one when j = 0 and zero for all

other values of j = 0.

22 1 Probability

0.2

(x)

x05

(b)

(x)

x05

(a)

Fig. 1.12 The uniform distribution for a discrete random variable whose values are 0, 1, ... ,5.

(a) The pmf and (b) is the corresponding cdf

Figure 1.12 shows the pmf for a random variable consisting of six samples which

are assumed to take the values 0, 1, ...,5.

Example 1.16 Study the statistical distribution of rounding errors in computer arith-

metic.

The truncation or rounding operation is required after fixed and floating point

number multiplication and also after floating point number addition. Rounding or

truncation is employed to reduce the number of bits back to their original size n,

say. Without loss of generality, we assume the inputs to be fractions with the binary

point at the left such that the weight of the most significant bit is 2

−1

and the weight

of the least significant bit (LSB) is 2

−n

. Figure 1.13 shows the location of the binary

point for the fixed-point number and also shows the bits that will be truncated or

rounded.

Truncating the extra bits to the right of LSB results in an error e whose magnitude

varies approximately in the range

−2

−n

≤ e ≤ 2

−n

(1.55)

Assume the number of bits to be truncated is m. In that case, our truncated data has

m bits and the number of possible error samples is k = 2 × 2

− 1. The factor 2

comes from the fact that the error could be positive or negative.

Define the discrete random variable E that corresponds to the rounding or trun-

cation error. Since the probability of any truncation error is equally likely, we have

p(e) =

(m+1)

−1

Fig. 1.13 Truncation of a

fractional number from

n + m bits to n bits

Quantization bits

. . .

Truncated bits

Binary point

1.23 Bernoulli (Binary) RV 23

1.23 Bernoulli (Binary) RV

Many systems in communications have two outcomes. For example, a received

packet might be error-free or it might contain an error. For a router or a switch,

a packet might arrive at a given time step or no packet arrives. Consider a chance

experiment that has two mutually exclusive outcomes A and

A that occur with prob-

abilities p and q, respectively. We define the discrete random variable X where

X = 1 when A occurs and X = 0 when

A occurs. We can write

p(1) = p (1.56)

p(0) = q (1.57)

where q = 1 − p. Alternatively, p(x) can be expressed by a single equation in the

form

p(x) = q δ(x) + p δ(x −1) (1.58)

The mean and variance for X are

μ = p (1.59)

= p (1 − p) (1.60)

Figure 1.14(a) shows the pmf for the binary distribution and Fig. 1.14(b) shows

the cdf.

Example 1.17 The 50/50 draw is one of the traditions of a typical minor lacrosse

or baseball sports events. Spectators purchase numbered tickets. One of the tickets

is picked at random and half the proceeds goes to the winner and the rest goes to

support the team (or the executive council might just use the money for their own

purposes). Assume you purchased one ticket and there was a total of 100 entries at

the start of the draw. What are your chances of winning or losing? How much would

your winnings be?

(x)p

(x)

x01

(b)

x01

(a)

Fig. 1.14 The binary distribution. (a) The pmf and (b) is the corresponding cdf

24 1 Probability

The total number of entries is 100, and the probabilities of winning or losing are

p =

100

= 0.01

q = 1 − p = 0.99

Assuming the purchase price of the ticket is $1, the winner takes $50. The money

won would be $49.

1.24 Geometric RV

This distribution is encountered when success, event A, occurs after n failures. This

is the case when several devices are attached to a bus and compete for access. The

probability of success is a and the probability of failure is b = 1 −a.

The pmf is the probability of success after n repeated failures and is given by

p(N = n) = ab

for n ≥ 0 (1.61)

Alternatively, p(n) can be expressed by a single equation in the form

p(n) =



i≥0

δ(n −i)forn ≥ 0 (1.62)

The mean and variance for N are

μ =

(1.63)

(1.64)

Example 1.18 Assume packets arrive at a certain device with probability a at a

given time slot. The probability that a packet does not arrive at a time slot is

b = 1 −a.

(a) What is the probability that we have to wait for n time slots before a packet

arrives?

(b) What is the average number of time slots between packet arrivals?

(a) The probability that we have to wait for n time slots before a packet ar-

rives is

p(n) = ab

(b) The average number of time slots between packet arrivals is given by

E[n] =

∞



i=0

np(n) =

∞



i=0

nab