Gebali F. Analysis Of Computer And Communication Networks

Подождите немного. Документ загружается.

3.6 Markov Matrices 75

Figure 3.5 shows the state of the channel and the transition probabilities between

these states.

1. The channel remains in the idle state with probability u

2. The channel moves from idle to transmitting state with probability u

3. The channel moves from idle to the collided state with probability 1 −u

−u

The other transitions are explained in the same way. We organize our state transi-

tion matrix such that first row or column corresponds to the idle state i. The second

row or column correspond to the collided state. The third row or column corresponds

to transmit state t

,etc.Forn transmit states, the transition matrix will have the

dimension (n + 2) ×(n + 2):

P =

⎡

⎢

⎣

00··· u

1 −u

−u

1 −u

−u

00··· 1 −u

−u

0 ··· u

0001··· 0

0000··· 0

⎤

⎥

⎦

3.6 Markov Matrices

The definition of the transition matrix P results in a matrix with peculiar properties:

1. The number of rows equals the number of columns. Thus P is a square matrix.

2. All the elements of P are real numbers. Thus P is a real matrix.

3. 0 ≤ p

≤ 1 for all values of i and j. Thus P is a nonnegative matrix.

4. The sum of each column is exactly 1 (i.e.,



j=1

= 1).

5. The magnitude of all eigenvalues obey the condition

≤ 1. Thus the spectral

radius of P equals 1.

6. At least one of the eigenvalues of P equals 1.

From all the above properties we conclude that the transition matrix is square,

real, and nonnegative. Such a matrix is termed column stochastic matrix or Markov

matrix. Notice that all column stochastic matrices are a subset of nonnegative ma-

trices. Thus nonnegative matrices need not be column stochastic.

Nonnegative matrices have many interesting properties related to their eigen-

values and eigenvectors but this is beyond the scope of this book [4]. The above

mentioned properties have implications on the eigenvalues of the transition matrix.

The following theorem indicates one such implication.

Theorem 3.1 Let P be any m × m column stochastic matrix. Then P has 1 as an

eigenvalue [4].

76 3 Markov Chains

Proof We know that if λ is an eigenvalue of P, then the determinant of the charac-

teristic equation must vanish, i.e.

det

(

P −λI

)

= 0 (3.13)

where I is an m × m unit matrix. By Assuming that P has 1 as an eigenvalue, then

the determinant is given by

det

(

P −1 ×I

)



−1 p

··· p

−1 ··· p

··· p

−1



(3.14)

where |A| indicates the determinant of matrix A. The determinant will not change

if we add all the remaining rows to the first row

det

(

P −1 ×I

)





−1



−1 ···



−1

−1 ··· p

··· p

−1



(3.15)

But the sum of the elements in each column is 1, and the first row of the above

determinant will be zero. As a result, the determinant is zero and this proves that 1

is an eigenvalue of P.

Conversely, assume that (3.13) is satisfied for some value of λ. In that case we

can write an equation similar to (3.15), namely:

det

(

P −1 ×I

)





−λ



−λ ···



−λ

−1 ··· p

··· p

−1



(3.16)

3.6 Markov Matrices 77

But we know that this determinant is zero. This is true for all values of p

which

implies that the elements in the first row of the matrix must be zero. Thus we must

have



−λ = 0 (3.17)

But the sums in the above equation is equal to 1 independent of the value of i.

Thus we must have

1 −λ = 0 (3.18)

The above equation implies that λ = 1 is a root of the equation which proves the

second part of the theorem.

The following theorem will prove useful when we start multiplying Markov ma-

trices to perform transient analysis on our Markov chain. The theorem essentially

explains the effect of premultiplying any matrix by a column stochastic matrix.

Theorem 3.2 The sum of columns of any matrix A will not change when it is pre-

multiplied by a column stochastic matrix P.

Proof When A is premultiplied by P we get matrix B.

B = PA (3.19)

Element b

is given by the usual matrix product formula



k=1

(3.20)

The sum of the jth column of matrix B is denoted by σ

(B) and is given by

(B) =



i=1



i=1



k=1

(3.21)

Now reverse the order of summation on the right-hand side of the above equation:

(B) =



k=1



i=1

(3.22)

Because P is column stochastic we have

(P) =



i=1

= 1 (3.23)

78 3 Markov Chains

Therefore, (3.22) becomes

(B) =



i=1



k=1

(3.24)

= σ

(A) (3.25)

Thus we proved that sum of columns of a matrix does not change when the matrix

is premultiplied by a column stochastic matrix.

3.6.1 The Diagonals of P

We mentioned above the significance of each element p

of the transition matrix P

as the probability of making a transition from state j to state i. Further insight can be

gained for Markov chains representing queues. Queuing systems are a special type of

Markov chains in which customers arrive and lineup to be serviced by servers. Thus

a queue is characterized by the number of arriving customers at a given time step,

the number of servers, the size of the waiting area for customers, and the number

customers that can leave in one time step.

The state of a queuing system corresponds to the number of customers in the

queue. If we take the lineup for a bank as an example, then the queue size increases

when new customers arrive. The number of arriving customers could be one in some

cases or many in others. This depends on the specifics of the situation. For example,

if there is only one door to the bank, then we could expect at most one customer

to arrive at any time. At the head of the queue, the number of servers also varies

depending on how many bank tellers are ready, or disposed, to serve the customers.

If there is only one teller, then we expect the size of the queue to decrease by at

most one each time a customer is served. The duration of the service time also

varies depending on the type of transaction being done.

The diagonals of P reflect the queuing system characteristics. Table 3.2 illustrates

the significance of each diagonal of the matrix P.

Table 3.2 Significance of diagonals of P

Diagonal Significance

Main probabilities queue will retain its size

1st upper probabilities queue size will decrease by one

2nd upper probabilities queue size will decrease by two

3rd upper probabilities queue size will decrease by three

1st lower probabilities queue size will increase by one

2nd lower probabilities queue size will increase by two

3rd lower probabilities queue size will increase by three

3.7 Eigenvalues and Eigenvectors of P 79

3.7 Eigenvalues and Eigenvectors of P

The eigenvalues and eigenvectors of the transition matrix P will prove to be of ut-

most importance in the analyses of this book. The following theorem makes certain

predictions about the eigenvector corresponding to the eigenvalue λ = 1.

Theorem 3.3 Given a column stochastic matrix P and the eigenvector x corre-

sponding to the eigenvalue λ = 1, the sum of the elements of x is nonzero and

could be taken as unity, i.e. σ (x) = 1.

Proof The eigenvector x corresponding to λ = 1 satisfies the equation

Px= x (3.26)

We can write the above equation as

(

P −I

)

x = 0 (3.27)

This is a system of linear equation with an infinite number of solutions since the

matrix

(

P −I

)

is rank deficient (i.e., rank(P) < m). To get a unique solution for x,

we need one extra equation which we choose as

σ (x) = 1 (3.28)

We cannot choose the sum to be zero since this is a trivial solution. Any nonzero

value is acceptable. We choose to have σ (x) = 1 for reasons that will become

apparent later on. This proves the theorem.

The following theorem makes certain predictions about the sum of elements of

the other eigenvectors of P corresponding to the eigenvalues λ<1.

Theorem 3.4 Given a column stochastic matrix P and an eigenvector x corre-

sponding to the eigenvalue λ = 1, the sum of the elements of x must be zero, i.e.

σ (x) = 0.

Proof The eigenvector x satisfies the equation

Px= λ x (3.29)

The sum of columns of both sides of the above equation are equal

σ (Px) = λσ(x) (3.30)

From Theorem 3.2, on page 77, we are assured that the sum of the elements of x

will not change after being multiplied by matrix P. Thus we can write

σ (Px) = σ (x) (3.31)

80 3 Markov Chains

From the above two equations we have

σ (x) = λσ (x) (3.32)

σ (x)(1 −λ) = 0 (3.33)

Since λ = 1, the only possible solution to the above equation is σ (x) = 0. This

proves the theorem.

Example 3.9 Verify Theorems 3.3 and 3.4 for the Markov matrix

P =

⎡

⎢

⎣

0.30.100.2

0.10.60.30.1

0.40.20.40.5

0.20.10.30.2

⎤

⎥

⎦

MATLAB gives the following eigenvectors and corresponding eigenvalues:

[X,D] = eig(P)

-0.1965 0.5887 -0.1002 -0.4286

-0.6309 0.3983 -0.7720 0.1644

-0.6516 -0.5555 0.5190 -0.4821

-0.3724 -0.4315 0.3532 0.7463

1.0000 0 0 0

0 0.2211 0 0

0 0 0.3655 0

0 0 0 -0.0866

We have to normalize our eigenvectors so that the sum of the components of the first

column, which corresponds to λ = 1 is one.

X = X/sum(X(:,1))

0.1061 -0.3179 0.0541 0.2315

0.3408 -0.2151 0.4169 -0.0888

0.3520 0.3001 -0.2803 0.2604

0.2011 0.2330 -0.1907 -0.4031

3.8 Constructing the State Transition Matrix P 81

We can write, ignoring rounding errors,

(X) = 1

(X) = 0

3.8 Constructing the State Transition Matrix P

The state transition matrix P is the key to analyzing Markov chains and queues. To

construct the matrix the following steps are usually followed [3].

1. Verify that the system under study displays the Markov property. In other words,

ensure that transition to a new state depends only on the current state.

2. All possible states of the system are identified and labeled. The labeling of the

states is arbitrary although some labeling schemes would render the transition

matrix easier to visualize.

3. All possible transitions between the states are either drawn on the state transi-

tion diagram, or the corresponding elements of the state transition matrix are

identified.

4. The probability of every transition in the state diagram is obtained.

5. The transition matrix is constructed.

6. Relabeling of the states is always possible. That will change the locations of the

matrix elements and make the structure of the matrix more visible. This rear-

rangement will still produce a column stochastic matrix and will not disturb its

eigenvalues or the directions of its eigenvectors.

Example 3.10 The closing price of a certain stock on a given weekday is either

falling or rising compared to the previous day’s price. If the price stays the same,

then it is classified as rising if the previous day’s trend was rising, and vice versa.

The probabilities of price transitions between these two states are shown in Fig. 3.6.

Construct state transition matrix.

The price of the stock has only two states, falling (s

) or rising (s

). The transition

matrix will be

Fig. 3.6 Day-to-day closing

price fluctuations of a certain

stock

falling

0.3

rising

0.6

0.7

0.4

82 3 Markov Chains

P =



0.30.6

0.70.4



3.9 Transient Behavior

From (3.8) on page 70 we can write the distribution vector at time step n = 1as

s(1) = Ps(0) (3.34)

and

s(2) = Ps(1) (3.35)

= P

[

Ps(0)

]

(3.36)

= P

s(0) (3.37)

and we can generalize to express the distribution vector at step n as

s(n) = P

s(0) n = 0, 1, 2, ... (3.38)

This equation allows us to calculate the distribution vector at the nth time step

given the transition matrix and the initial distribution vector s(0).

Example 3.11 In Example 3.6, on page 72, what is the probability that our truck is

in Colwood after five deliveries assuming that it was Langford initially?

We are looking for element p

in matrix P

. Using any mathematical tool such

as MAPLE or MATLAB, we get

⎡

⎣

0.199 0.20.200

0.288 0.277 0.278

0.513 0.523 0.522

⎤

⎦

Hence the required probability is 0.2.

Example 3.12 Assume a ball falls on the pegs shown in Fig. 3.7. The pegs are setup

such that the ball must hit a peg at each level and bounce off one of the two pegs

immediately below. The location of the ball at the bottom bucket indicates the prize

to be won.

(a) Define a Markov chain describing the state of the ball.

(b) Write down the transition matrix.

hole.

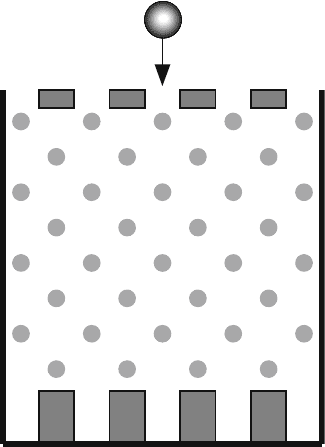
3.9 Transient Behavior 83

Fig. 3.7 A ball falling

through a maze of pegs

row 0

row 1

row 2

row 3

row 4

row 5

row 6

row 7

row 8

(d) Determine the probability of hitting the middle bucket.

(e) Assume the money to be won is given by the vector

w =



$5 $1 $10 $1 $5



Determine the average amount of money that could be won.

Since the next location of the ball depends only on its present location, we can

describe this system using Markov chains.

(a) We can model this system as a Markov chain with nine states s

to s

, as indi-

cated in the figure. State s

(n) indicates that the ball is at column i and row n

in the game. The rows are numbered starting with zero at the top row. Thus our

distribution vector could be written as

s =





where at even time steps the even states could be occupied and at odd time steps

only the odd states could be occupied.

84 3 Markov Chains

(b) The transition matrix is given by

P =

⎡

⎢

⎣

00.50000000

10 0.5000000

00.50 0.500000

00 0.50 0.50 0 0 0

0000.50 0.50 0 0

00000.50 0.50 0

000000.50 0.50

0000000.50 1

00000000.50

⎤

⎥

⎦

s(0) =



000010000



(d) After eight iterations, the ball finally falls into one of the buckets. Thus the

distribution vector after eight iterations is given by

s(8) = P

s(0)



0.11 0 0.25 0 0.28 0 0.25 0 0.11



Note that the only valid states are the ones that correspond to a bucket loca-

tions at the bottom of the figure. This explains the zeros in the odd locations 1,

3, 5, and 7. The probability of settling into the middle bucket is s

= 0.28.

(e) The average winnings are given by

= W

(8) + W

(8)

= $4.4

It is interesting that if hundreds of balls are dropped at the center toward the

bottom, then their distribution at the bottom barrels is bell-shaped and their

number is the binomial coefficients [5]

Example 3.13 A computer memory system is composed of very fast on-chip cache,

fast on-board RAM, and slow hard disk. When the computer is accessing a block

from each memory system, the next block required could come from any of the three

available memory systems. This is modeled as a Markov chain with the state of the

system representing the memory from which the current block came from: state s

corresponds to the cache, state s

corresponds to the RAM, and state s

corresponds

to the hard disk. The transition matrix is given by

P =

⎡

⎣

0.70.10

0.20.70.1

0.10.20.9

⎤

⎦