Gebali F. Analysis Of Computer And Communication Networks
Подождите немного. Документ загружается.

146 4 Markov Chains at Equilibrium
4.16 A queuing system is described by the following transition matrix.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎣
0.80.70 ···
0.20.10.7 ···
00.20.1 ···
000.2 ···
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎦
Find the steady-state distribution vector using the difference equations ap-
proach.
4.17 A queuing system is described by the following transition matrix.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎣
0.90.20 ···
0.10.70.2 ···
00.10.7 ···
000.1 ···
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎦
Find the steady-state distribution vector using the difference equations ap-
proach.
4.18 A queuing system is described by the following transition matrix.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎣
0.85 0.35 0 ···
0.15 0.50.35 ···
00.15 0.5 ···
000.15 ···
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎦
Find the steady-state distribution vector using the difference equations ap-
proach.
4.19 A queuing system is described by the following transition matrix.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0.70.60 0 ···
0.20.10.60 ···
0.10.20.10.6 ···
00.10.20.1 ···
000.10.2 ···
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
Find the steady-state distribution vector using the difference equations ap-
proach.
Problems 147
Finding s Using Z-Transform
4.20 Given the following state transition matrix, find the first 10 components of the
equilibrium distribution vector using the z-transform approach.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎣
0.80.30 ···
0.20.50.3 ···
00.20.5 ···
000.2 ···
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎦
4.21 Given the following state transition matrix, find the first 10 components of the
equilibrium distribution vector using the z-transform approach.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎣
0.95 0.45 0 ···
0.05 0.50.45 ···
00.05 0.5 ···
000.05 ···
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎦
4.22 Given the following state transition matrix, find the first 10 components of the
equilibrium distribution vector using the z-transform approach.
P
=
⎡
⎢
⎢
⎢
⎢
⎢
⎣
0.95 0.45 0 ···
0.05 0.50.45 ···
00.05 0.5 ···
000.05 ···
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎦
4.23 Given the following state transition matrix, find the first 10 components of the
equilibrium distribution vector using the z-transform approach.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎣
0.86 0.24 0 ···
0.14 0.62 0.24 ···
00.14 0.62 ···
000.14 ···
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎦
148 4 Markov Chains at Equilibrium
4.24 Given the following state transition matrix, find the first 10 components of the
equilibrium distribution vector using the z-transform approach.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎣
0.93 0.27 0 ···
0.07 0.66 0.27 ···
00.07 0.66 ···
000.07 ···
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎦
4.25 Given the following state transition matrix, find the first 10 components of the
equilibrium distribution vector using the z-transform approach.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0.512 0.3584 0 0 ···
0.384 0.4224 0.3584 0 ···
0.096 0.1824 0.4224 0.3584 ···
0.008 0.0344 0.1824 0.4224 ···
00.0024 0.0344 0.1824 ···
00 0
.0024 0.0344 ···
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
4.26 Given the following state transition matrix, find the first 10 components of the
equilibrium distribution vector using the z-transform approach.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0.720 0.4374 0 0 ···
0.243 0.4374 0.4374 0 ···
0.027 0.1134 0.4374 0.4374 ···
0.001 0.0114 0.1134 0.4374 ···
00.0004 0.0114 0.1134 ···
00 0.0004 0.0114 ···
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
4.27 Given the following state transition matrix, find the first 10 components of the
equilibrium distribution vector using the z-transform approach.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0.9127 0.3651 0 0 ···
0.0847 0.5815 0.3651 0 ···
0.0026 0.0519 0.5815 0.3651 ···
00.0016 0.0519 0.5815 ···
000.0016 0.0519 ···
0000.0016 ···
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
References 149
4.28 Given the following state transition matrix, find the first 10 components of the
equilibrium distribution vector using the z-transform approach.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0.6561 0.5249 0 0 ···
0.2916 0.3645 0.5249 0 ···
0.0486 0.0972 0.3645 0.5249 ···
0.0036 0.0126 0.0972 0.3645 ···
0.0001 0.0008 0.0126 0.0972 ···
000.0008 0.0126 ···
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
4.29 Given the following state transition matrix, find the first 10 components of the
equilibrium distribution vector using the z-transform approach.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0.512 0.4096 0 0 ···
0.384 0.4096 0.4096 0
···
0.096 0.1536 0.4096 0.4096 ···
0.008 0.0256 0.1536 0.4096 ···
0.0001 0.0016 0.0256 0.1536 ···
000.0016 0.0256 ···
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
References
1. M.E. Woodward, Communication and Computer Networks, IEEE Computer Society Press,
Los Alamitos, CA, 1994.

Chapter 5
Reducible Markov Chains
5.1 Introduction
Reducible Markov chains describe systems that have particular states such that once
we visit one of those states, we cannot visit other states. An example of systems
that can be modeled by reducible Markov chains is games of chance where once
the gambler is broke, the game stops and the casino either kicks him out or gives
him some compensation (comp). The gambler moved from being in a state of play
to being in a comp state and the game stops there. Another example of reducible
Markov chains is studying the location of a fish swimming in the ocean. The fish
is free to swim at any location as dictated by the currents, food, or presence of
predators. Once the fish is caught in a net, it cannot escape and it has limited space
where it can swim.
Consider the transition diagram in Fig. 5.1(a). Starting at any state, we are able
to reach any other state in the diagram directly, in one step, or indirectly, through
one or more intermediate states. Such a Markov chain is termed irreducible Markov
chain for reasons that will be explained shortly. For example, starting at s
1
, we can
directly reach s
2
and we can indirectly reach s
3
through either of the intermediate
s
2
or s
5
. We encounter irreducible Markov chains in systems that can operate for
long periods of time such as the state of the lineup at a bank, during business hours.
The number of customers lined up changes all the time between zero and maxi-
mum. Another example is the state of buffer occupancy in a router or a switch. The
buffer occupancy changes between being completely empty and being completely
full depending on the arriving traffic pattern.
Consider now the transition diagram in Fig. 5.1(b). Starting from any state, we
might not be able to reach other states in the diagram, directly or indirectly. Such a
Markov chain is termed reducible Markov chain for reasons that will be explained
shortly. For example, if we start at s
1
, we can never reach any other state. If we
startatstates
4
, we can only reach state s
5
. If we start at state s
3
, we can reach all
other states. We encounter reducible Markov chains in systems that have terminal
conditions such as most games of chance like gambling. In that case, the player
keeps on playing till she loses all her money or wins. In either cases, she leaves the
game. Another example is the game of snakes and ladders where the player keeps
F. Gebali, Analysis of Computer and Communication Networks,
DOI: 10.1007/978-0-387-74437-7
5,
C
Springer Science+Business Media, LLC 2008
151
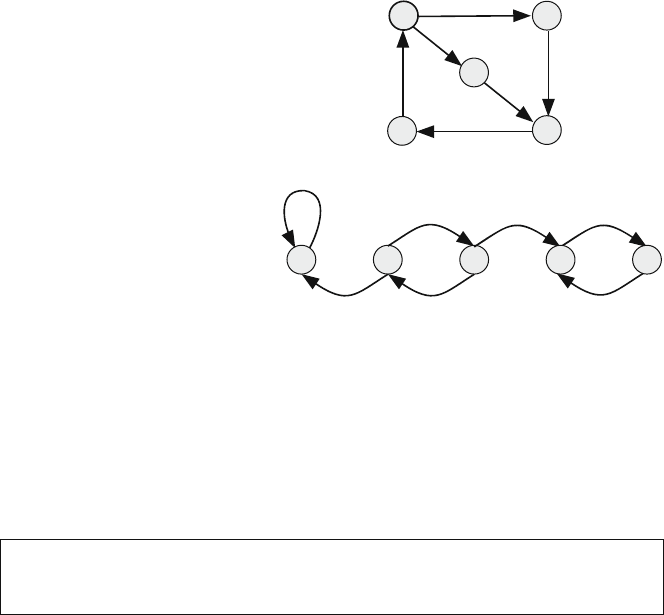
152 5 Reducible Markov Chains
Fig. 5.1 State transition
diagrams. (a) Irreducible
Markov chain. (b) Reducible
Markov chain
1
2 3 4 5
1
3
4
2
5
(a)
(b)
on playing but cannot go back to the starting position. Ultimately, the player reaches
the final square and could not go back again to the game.
5.2 Definition of Reducible Markov Chain
The traditional way to define a reducible Markov chain is as follows.
A Markov chain is irreducible if there is some integer k > 1 such that all
the elements of P
k
are nonzero.
What is the value of k? No one seems to know; the only advice is to keep on
multiplying till the conditions are satisfied or computation noise overwhelms us!
This chapter is dedicated to shed more light on this situation and introduce, for
the first time, a simple and rigorous technique for identifying a reducible Markov
chain. As a bonus, the states of the Markov chain will be simply classified too with-
out too much effort on our part.
5.3 Closed and Transient States
We defined an irreducible (or regular) Markov chain as one in which every state
is reachable from every other state either directly or indirectly. We also defined a
reducible Markov chain as one in which some states cannot reach other states. Thus
the states of a reducible Markov chain are divided into two sets: closed state (C)
and transient state (T ). Figure 5.2 shows the two sets of states and the directions of
transitions between the two sets of states.
When the system is in T , it can make a transition to either T or C. However, once
our system is in C, it can never make a transition to T again no matter how long we
iterate. In other words, the probability of making a transition from a closed state to
a transient state is exactly zero.
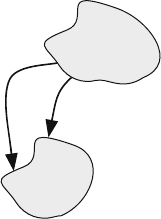
5.4 Transition Matrix of Reducible Markov Chains 153
Fig. 5.2 Reducible Markov
chain with two sets of states.
There are no transitions from
the closed states to the
transient states as shown.
Transient
State
Closed
State
When C consists of only one state, then that state is called an absorbing state.
When s
i
is an absorbing state, we would have p
ii
= 1. Thus inspection of the
transition matrix quickly informs us of the presence of any absorbing states since
the diagonal element for that state will be 1.
5.4 Transition Matrix of Reducible Markov Chains
Through proper state assignment, the transition matrix P for a reducible Markov
chain could be partitioned into the canonic form
P =
CA
0T
(5.1)
where
C = square column stochastic matrix
A = rectangular nonnegative matrix
T = square column substochastic matrix
Appendix D defines the meaning of nonnegative and substochastic matrices. The
matrix C is a column stochastic matrix that can be studied separately from the rest
of the transition matrix P. In fact, the eigenvalues and eigenvectors of C will be used
to define the behavior of the Markov chain at equilibrium.
The states of the Markov chain are now partitioned into two mutually exclusive
subsets as shown below.
C = set of closed states belonging to matrix C
T = set of transient states belonging to matrix T
The following equation explicitly shows the partitioning of the states into two
sets, closed state C and transient state T .
CT
P =
C
T
CA
0T
(5.2)

154 5 Reducible Markov Chains
Example 5.1 The given transition matrix represents a reducible Markov chain.
P =
s
1
s
2
s
3
s
4
s
1
s
2
s
3
s
4
⎡
⎢
⎢
⎣
0.80 0.10.1
00.50 0.2
0.20.20.90
00.30 0.7
⎤
⎥
⎥
⎦
where the states are indicated around P for illustration. Rearrange the rows and
columns to express the matrix in the canonic form in (5.1) or (5.2) and identify
the matrices C, A, and T. Verify the assertions that C is column stochastic, A is
nonnegative, and T is column substochastic.
After exploring a few possible transitions starting from any initial state, we see
that if we arrange the states in the order 1, 3, 2, 4 then the following state matrix is
obtained
P =
s
1
s
3
s
2
s
4
s
1
s
2
s
3
s
4
⎡
⎢
⎢
⎣
0.80.10 0.1
0.20.90.20
000.50.2
000.30.7
⎤
⎥
⎥
⎦
We see that the matrix exhibits the reducible Markov chain structure and matrices
C, A, and T are
C =
0.80.1
0.20.9
A =
00.1
0.20
T =
0.50.2
0.30.7
The sum of each column of C is exactly 1, which indicates that it is column
stochastic. The sum of columns of T is less than 1, which indicates that it is column
substochastic.
The set of closed states is C ={1, 3}and the set of transient states is T ={2, 4}.
Starting in state s
2
or s
4
, we will ultimately go to states s
1
and s
3
. Once we
are there, we can never go back to state s
2
or s
4
because we entered the closed
states.
Example 5.2 Consider the reducible Markov chain of the previous example. As-
sume that the system was initially in state s
3
. Find the distribution vector at 20 time
step intervals.

5.5 Composite Reducible Markov Chains 155
We do not have to rearrange the transition matrix to do this example. We have
P =
⎡
⎢
⎢
⎣
0.80 0.10.1
00.50 0.2
0.20.20.90
00.30 0.7
⎤
⎥
⎥
⎦
The initial distribution vector is
s =
0010
t
The distribution vector at 20 time step intervals is
s(20) =
0.3208 0.0206 0.6211 0.0375
t
s(40) =
0.3327 0.0011 0.6642 0.0020
t
s(60) =
0.3333 0.0001 0.6665 0.0001
t
s(80) =
0.3333 0.0000 0.6667 0.0000
t
We note that after 80 time steps, the probability of being in the transient state
s
2
or s
4
is nil. The system will definitely be in the closed set composed of states s
1
and s
3
.
5.5 Composite Reducible Markov Chains
In the general case, the reducible Markov chain could be composed of two or more
sets of closed states. Figure 5.3 shows a reducible Markov chain with two sets of
closed states. If the system is in the transient state T, it can move to either sets of
closed states, C
1
or C
2
. However, if the system is in state C
1
, it cannot move to T
or C
2
. Similarly, if the system is in state C
2
, it cannot move to T or C
1
. In that case,
the canonic form for the transition matrix P for a reducible Markov chain could be
expanded into several subsets of noncommunicating closed states
P =
⎡
⎣
C
1
0A
1
0C
2
A
2
00T
⎤
⎦
(5.3)
where
C
1
and C
2
= square column stochastic matrices
A
1
and A
2
= rectangular nonnegative matrices
T = square column substochastic matrix
Since the transition matrix contains two-column stochastic matrices C
1
and C
2
,
we expect to get two eigenvalues λ
1
= 1 and λ
2
= 1 also. And we will be getting
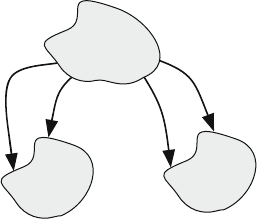
156 5 Reducible Markov Chains
Fig. 5.3 A reducible Markov
chain with two sets of closed
states
Transient
State T
Closed
State
C
1
Closed
State
C
2
two possible steady-state distributions based on the initial value of the distribution
vector s(0)—more on that in Sections 5.7 and 5.9.
The states of the Markov chain are now divided into three mutually exclusive sets
as shown below.
1. C
1
= set of closed states belonging to matrix C
1
2. C
2
= set of closed states belonging to matrix C
2
3. T = set of transient states belonging to matrix T
The following equation explicitly shows the partitioning of the states.
P =
C
1
C
2
T
C
1
C
2
T
⎡
⎣
C
1
0A
1
0C
2
A
2
00T
⎤
⎦
(5.4)
Notice from the structure of P in (5.4) that if we were in the first set of closed
state C
1
, then we cannot escape that set to visit C
2
or T . Similarly, if we were in the
second set of closed state C
2
, then we cannot escape that set to visit C
1
or T .Onthe
other hand, if we were in the set of transient states T , then we can not stay in that
set since we will ultimately fall into C
1
or C
2
.
Example 5.3 You play a coin tossing game with a friend. The probability that one
player winning $1 is p, and the probability that he loses $1 is q = 1 − p. As-
sume the combined assets of both players is $6 and the game ends when one of the
players is broke. Define a Markov chain whose state s
i
means that you have $i and
construct the transition matrix. If the Markov chain is reducible, identify the closed
and transient states and rearrange the matrix to conform to the structure of (5.3)
or (5.4).
Since this is a gambling game, we suspect that we have a reducible Markov chain
with closed states where one player is the winner and the other is the loser.
