Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.

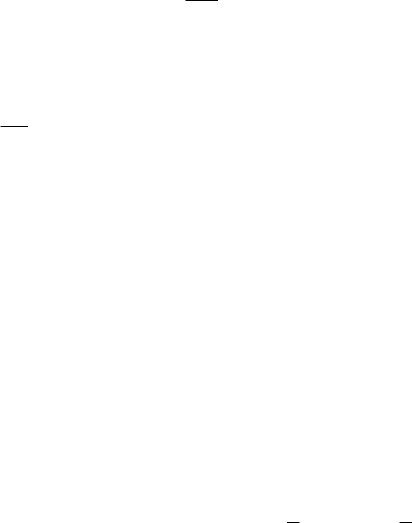
51
),()( xtftx
=
&
. (2.40)
Если правые части СДУ не зависят явно от
t
, т.е.
)()( xftx
=
&
или
),()( gxftx
=
&
, (2.41)
то такая СДУ называется системой с постоянными параметрами (иногда
её называют автономной или стационарной системой).
Далее мы чаще всего будем рассматривать системы вида (2.41).
Обычно вектор-функции в правых частях СДУ (2.39) – (2.41) тако-
вы, что в векторном пространстве
n
R
существует одна или несколько
точек
i
a
, т. е.
i
ax =
,
mi
,1
=
таких, что
0)(),(),,( ===
iii
afatfgatf
. (2.42)
В этих точках производные по времени всех переменных
)(txx
ii
=
,
ni ,1=
, очевидно, одновременно обращаются в нуль. Такие точки назы-
ваются о со бым и то чкам и или по ло жен ия ми р ав нов еси я (см. па-
раграф 1.1) соответствующей системы.
Реше нием дифференциального уравнения (2.36) или (2.37) назы-
вается такая функция времени
)(tx
, которая при подстановке ее в диф-
ференциальное уравнение вместо x, обращает уравнение в тождество при
всех
0
≥
t
и удовлетворяет начальному условию вида
0
)0( xx =
. (2.43)
Здесь
0
x
– начальное значение решения
)(tx
[9].
Например, уравнение тиристорного усилителя (см. рис. 1.21)
Tkgyy /)(
−
−
=
&
, (2.44)
где
g
– постоянная величина, имеет решение
)1()(
0
T
t
T
t
ekgeyty
−−
−+=
. (2.45)
Здесь
0
y
– начальное значение выходной переменной тиристорного уси-
лителя.
Аналогично, р еш ение м СДУ (2.38) – (2.40) или (2.41) является век-
тор-функция времени
)(tx
, которая обращает СДУ в систему тождеств
52
при всех
0
≥
t
и удовлетворяет начальным условиям.
Как видно из выражения (2.45), само ДУ не полностью определяет
свое решение. Действительно, например, в случае уравнения (2.44), при-
давая различные значения величине
0
y
, мы будем получать различные
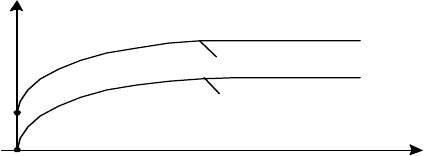
его решения, два из которых при
0
0
=y
и
5,0
0
=y
показаны на рис. 2.3.
Другими словами, для полного определения какого-либо решения
СДУ необходимо, кроме самой СДУ, задать вектор начальных условий
0
x
, который определяет значения решения
)(tx
при
0
=
t
.
Поскольку решение СДУ зависит и от начальных условий
0
x
, и от
возмущающей функции g, то его часто записывают так:
))(,,(
0
tgxtxx
=
– решение неоднородной СДУ,
),(
0
xtxx
=
– решение однородной СДУ.
Тогда при
0
=
t
получаем тождество
(
)
00
)0(,,0 xgxx
=
. (2.46)
Отметим, что СДУ в форме (2.38) – (2.41) называется нормальной фор-
мой СДУ или формой Коши. Задача отыскания решения СДУ, удовлетво-
ряющего, скажем (2.39) и (2.46), называется за дач ей Коши , а процесс
нахождения решения
))(,,(
0
tgxtxx
=
– инт егр иро ва ни ем СД У.
Если в решении
),(
0
xtxx
=
некоторой однородной СДУ заменить
вектор
0
x
вектором произвольных постоянных
T
n
cccc ][
21
K=
, то
решение
),()( сtxtx
=
будет являться, так называемым, о бщи м реше -
нием однородной СДУ (2.40) или однородной СДУ, соответствующей
неоднородной СДУ (2.39). Фактически, общее решение – это множество
y
t
0
0,5
y = 0,5
0
y = 0
0
Рис. 2.3

53
или семейство решений СДУ, содержащее все без исключения решения
однородной СДУ. Эти решения отличаются друг от друга только лишь
значениями произвольных постоянных.
Функция
),0,( gtxx
g
=
называется ч аст ны м р еш ени ем, а
функция
),,( gctxx
g
=
– полным или просто реш ен ием не од но ро д-
ной СДУ (2.39).
Методов решения нелинейной задачи Коши, когда функции в пра-
вой части СДУ (2.38) – (2.41) имеют произвольный вид, не существует.
Более того, некоторые СДУ могут вообще не иметь решения, определен-
ного при всех
),0[
∞
∈
t
. Известен ряд методов решения, иногда сами
решения, но лишь для некоторых типов СДУ.
Приведем примеры простейших ДУ и СДУ, а также их решений [15].
Пример 2.4. Неоднородное линейное дифференциальное уравнение
первого порядка и его решение:
)(tgx
=
&
,
∫
ττ+=
t
dgxgxtx
0
00
)(),,(
.
Пример 2.5. Нелинейное ДУ первого порядка в квазилинейной
форме и его решение:
xxfx )(
=
&
,
∫
ττ
=
t
dxf
exxtx
0
))((
00
),(
.
Пример 2.6. Линейное ДУ с переменным коэффициентом и его ре-
шение при
0
0
=x
:
txx /
=
&
,
tcxtx =),(
0
,
где с – произвольная величина. Заметим, что здесь
0
0
=x
, для всех ре-
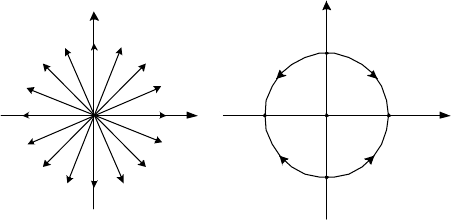
шений. Графиками решений являются прямые линии, исходящие из на-
чала координат (см. рис. 2.4). Интересно, что при
0
0
≠x
решений данно-
го ДУ не существует.
Пример 2.7. Нелинейное ДУ с зависимой от времени правой частью
и его решение
xtx /
−
=
&
,
22
00
),( txxtx −±=
.
54
Решение данного уравнения, как видно на рис. 2.5, существует либо в
интервале времени
],0[
0
xt∈
, либо
],0[
0
xt −∈
и изменяется, либо
от
0
x
до нуля, либо от –
0
x
до нуля.
Пример 2.8. Система линейных дифференциальных уравнений (ли-
нейная СДУ):
11
2xx
−
=
&
,
0
2
=
x
&
. (2.47)
Решением этой системы является вектор
=
−
20
2
10
0
),(
x
ex
xtx
t
,
где
10
x
,
20
x
– начальные значения переменных
1
x
,
2
x
.
Условия существования и единственности решений СДУ. В об-
щем случае СДУ, как видно из приведенных выше примеров, могут
иметь единственное решение, проходящее через заданную начальную
точку (примеры 2.4 или 2.8), а могут иметь несколько решений, прохо-
дящих через одну точку (см. пример 2.6, 2.7; рис. 2.4, 2.5).
Рис. 2.4 Рис. 2.5
С точки зрения качества описания той или иной динамической сис-
темы ее моделью в виде СДУ очень важно имеет ли СДУ единственное
решение или нет? Если решение единственное, то данная модель, оче-
видно, однозначно описывает движение динамической системы при тех
или иных начальных значениях, как, например, в случае СДУ (2.47). Если
же решение СДУ не единственное, то сказать каково же будет движение
x
t
x
0
-x
0
x
t
0

55
реальной динамической системы невозможно, так как невозможно опре-
делить какое из найденных решений СДУ отвечает действительному
движению системы. Так, например, в случае СДУ из примера 2.6, нет
никакой возможности определить по заданной модели и начальному ус-
ловию
0
0
=x
с какой же скоростью будет изменяться переменная
)(tx
в
реальной системе?
Условия, при которых СДУ имеет единственное решение, проходя-
щее через заданную точку, называются условиями существования и
единственности решений. Известно несколько видов условий существо-
вания и единственности решений СДУ [13, 15].
Чаще всего используются следующие условия.
СДУ (2.40) и ме ет е дин стве нное решение в некоторой окрест-
ности начальных значений, если одновременно выполняются следующие
условия:
а) все функции
),,,(
21 nii
xxxtff
K=
,
ni ,1=
непрерывны в той же
окрестности начальных значений, т.е.
),0(),0(lim
00
0
0
xfxf
ii
=
∆
±
δ
±
→∆
→δ
; (2.48)
б) выполнены условия Липшица по всем аргументам
n
xxx , ,
21
K
в той же окрестности, т.е. существует константа Липши-
ца N такая, что
( ) ( )
∑
−≤−
=
n
i
iiii
zxNztfxtf
1
,,
. (2.49)
Условие (2.49) можно заменить более жестким условием – ограни-
ченности в той же окрестности частных производных функций
),,,(
21 nii
xxxtff
K
=
по переменным
j
x
, т.е.
∞<≤
∂
∂
С
x
xtf
j
i
),(
,
nji ,1, =
, (2.50)
где C – некоторая константа.
Вектор x в СДУ (2.39) или (2.40) с точки зрения теории систем явля-
ется вектором состояний. Поэтому пространство, по осям координат ко-
торого отложены значения переменных
)( ),( ),(
21
txtxtx
n
K
в каж-
56
дый момент времени t, называется пространством состояний. Его можно
обозначить символом {x}. Решение
),(
0
xtxx =
некоторой однородной
СДУ определяет в пространстве состояний {x} некоторую кривую, про-
ходящую через точку
0
x
при
0
=
t
. Эта кривая называется траекторией
или интегральной кривой системы.
Если в пространстве состояний ввести еще одну ось и откладывать
на ней значения времени t, то получится
1
+
n
-мерное пространство {x,t}.
Указанные пространства позволяют дать наглядную интерпретацию ус-
ловий существования и единственности решений СДУ с постоянными и
переменным параметрами.
Если условия существования и единственности (2.48) и (2.49) или
(2.48) и (2.50) выполнены, то в случае однородной СДУ с постоянными
параметрами (2.41) через каждую точку и в пространстве состояний {x},
и в пространстве {x,t} проходит единственная интегральная кривая (тра-
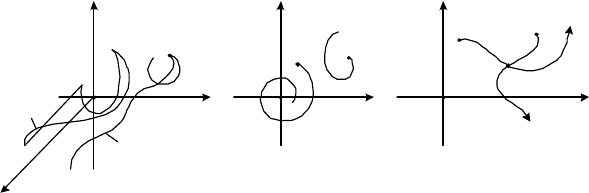
ектория), как показано на рис. 2.6 и рис. 2.7 (при
2
=
n
).
Другими словами, при выполнении условий существования и един-
ственности (2.48) и (2.49) или (2.48) и (2.50) траектории однородной СДУ
с постоянными параметрами (2.41) никогда не пересекаются.
Если же хотя бы одно из условий (2.48) или (2.49) не выполняется,
то через одну точку и пространства состояний {x} и пространства {x,t}
может проходить несколько траекторий (см. рис. 2.8), т.е. траектории
могут пересекаться (как, например, в точке а на рис. 2.8).
Рис. 2.6 Рис. 2.7 Рис. 2.8
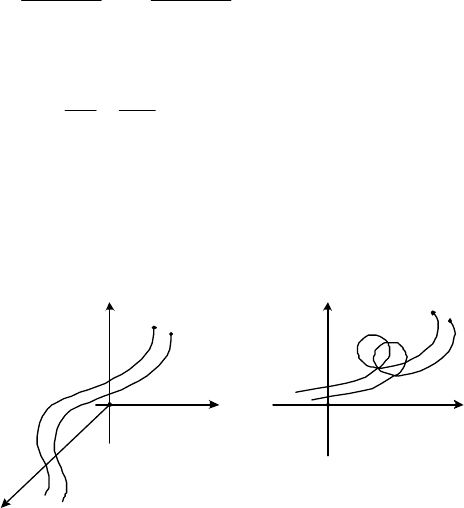
Совершенно иная ситуация имеет место в случае однородной СДУ с
переменными параметрами (2.40). Здесь при выполнении условий (2.48) и
(2.49) или (2.48) и (2.50) траектории не пересекаются только в простран-
стве {x,t}, как показано на рис. 2.9,а. В пространстве же состояний {x}
они могут пересекаться (рис. 2.9,б).
t
0
x
2
x
1
x''
x'
x
0
'
x
0
''
0
x
0
''
x
0
'
x
1
x
2
x
0
''
x
0
'
x
1
x
2
a
0
57
Первый интеграл. Понятие первого интеграла относится к одно-
родным СДУ вида (2.40) или (2.41). Пер вым и нтегр ало м СДУ назы-
вается функция
),(),,,(
21
xtxxxt
n
ϕ=ϕ K
(2.51)
определенная и непрерывная вместе со своими частными производными,
если при подстановке в нее произвольного решения
),(
0
xtxx =
мы по-
лучаем постоянную относительно t величину, т.е. функция
)),(,(
0
xtxtϕ
зависит только от
0
x
и не зависит от t. Это означает, что функция
),( xt
ϕ
(2.51) удовлетворяет условию
0)(
),(),(
1
=
∑
∂
ϕ
∂
+
∂
ϕ
∂
=ϕ
=
xf
x
xt
t
xt
i
n
i
i
&
, (2.52)
где
)(])()()([
21
xfxfxfxf
T
n
=K
– правая часть СДУ (2.41).
Здесь (и далее)
t
∂
ϕ∂
,
i
x∂
ϕ∂
– обозначение частной производной от
функции
),,,(
21 n
xxxt
K
ϕ
нескольких переменных по одной из этих пе-
ременных.
Справедливо и обратное утверждение: всякая функция
),,,(
21 n
xxxt
K
ϕ
, удовлетворяющая условию (2.52), является первым
интегралом однородной СДУ (2.41) [14, 15].
а) б)
x
1
x
2
x
0
'
x
0
''
t
x
2
x
1
x
0
'
x
0
''
Рис. 2.9
Первые интегралы находят широкое применение при исследовании
СДУ. В частности они могут быть применены для понижения порядка
СДУ. Действительно, в силу определения первого интеграла при всех t

58
имеет место равенство
сxxxt
n
=ϕ ),,,(
21
K
, (2.53)
где
с
– некоторая константа. Следовательно, с помощью (2.53) можно
выразить одну из переменных
i
x
,
ni ,1=
через остальные. Если теперь
полученное выражение подставить в СДУ, то число неизвестных в ней
окажется на единицу меньше. Если известно несколько – m первых инте-
гралов, причем
n
m
<
, то аналогичным путем можно понизить порядок
СДУ до величины
m
n
−
.
Первый интеграл обладает следующим интересным свойством. Ра-
венство (2.53) при фиксированном c определяет в
1
+
n
-мерном про-
странстве {x,t} некоторую поверхность. Оказывается, имеет место сле-
дующее. Если какая либо интегральная кривая некоторой СДУ имеет с
этой поверхностью хотя бы одну общую точку, то вся эта кривая лежит
на этой поверхности.
Приведем примеры первых интегралов СДУ [15].
Пример 2.9. Для линейной системы
,
,
,
213
132
321
xxx
xxx
xxx
−=
−=
−=
&
&
&
(2.54)
найти несколько первых интегралов.
Решение. Сложив уравнения (2.54) друг с другом, получим
211332321
xxxxxxxxx −+−+−=++
&&&
или
0
)(
321
=
+
+
dt
xxxd
. (2.55)
Следовательно,
1321
cxxx =++
, (2.56)
где
1
c
– некоторая постоянная величина.
Сравнивая равенство (2.56) с (2.53) или (2.55) с (2.52), заключаем,
что функция
321
1
)( xxxx ++=ϕ
является первым интегралом системы
линейных дифференциальных уравнений (2.54).

59
В данном случае можно найти еще один первый интеграл. С этой
целью умножим первое уравнение в (2.54) на
1
x
, второе на
2
x
, а третье на
3
x
, а затем снова сложим эти уравнения. В результате получим
0
332211
=++ xxxxxx
&&&
.
Левая часть этого равенства с учетом yравнений (2.54) является,
очевидно, половиной производной по времени от суммы
)(
2
3
2
2
2
1
xxx ++
, т.е.
0
)(
2
3
2
2
2
1
=
++
dt
xxxd
.
Следовательно, снова имеем равенство
2
2
3
2
2
2
1
cxxx =++
, (2.57)
где
2
c
– другая постоянная величина. Из равенства (2.57) следует, что
функция
2
3
2
2
2
12
)( xxxx ++=ϕ
– также является первым интегралом
линейной СДУ (2.54).
Отметим, что задача построения первых интегралов СДУ в общем слу-
чае чрезвычайна сложна. Некоторые приемы построения первых интегралов,
в ряде частных случаев правых частей СДУ, приводятся в [14, 15].
Как отмечалось выше, наличие нескольких первых интегралов неко-
торой СДУ позволяет понизить ее порядок. Покажем эту возможность на
примере.
Пример 2.10. Возвращаясь к рассмотренному примеру СДУ (2.54)
выразим из равенств (2.56) и (2.57) переменные
2
x
и
3
x
через
1
x
,
1
с
и
2
с
. После некоторых преобразований найдем
2
12
2
111
11
2
232
2
1
2
ccxxc
xc
x −+−+
−
=
, (2.58)
2
12
2
111
11
3
232
2
1
2
ccxxc
xc
x −+−−
−
=
. (2.59)
Подставляя полученные выражения в первое уравнение (2.54), получим

60
2
12
2
1111
232 ccxxcx −+−=
&
. (2.60)
Отметим, что
1
с
и
2
с
фактически произвольные постоянные. По-
этому с учетом начального условия
10
x
для переменной
1
x
система
уравнений (2.58) – (2.60), как и система (2.54), тоже содержит три произ-
вольных постоянных. Однако как дифференциальная система она имеет
порядок равный единице, что на два меньше по сравнению с порядком
СДУ (2.54). Это понижение порядка достигнуто, благодаря использова-
нию двух первых интегралов (2.56) и (2.57) данной системы дифферен-
циальных уравнений.
Независимость первых интегралов. В общем случае для каждой
СДУ можно построить много различных по виду первых интегралов. Од-
нако часть из них может являться просто комбинацией некоторых других
первых интегралов. Поэтому вводится понятие независимости первых
интегралов.
Пусть точка a не является положением равновесия (см. определение
(2.42)) однородной СДУ (2.41), т.е.
0)(
≠
af
.
Предположим для системы (2.41) построено k – первых интегралов:
)(
1
x
ϕ
,
)(
2
x
ϕ
,
K
,
)(
x
k
ϕ
.
Определение. Пусть однородная СДУ (2.41) порядка n имеет k пер-
вых интегралов. Тогда они называются н еза ви си мы ми в то чк е a или
просто независимыми, если функциональная
nk
×
матрица
∂
ϕ∂
=
=ax
j
i
x
x
J
)(
(2.61)
имеет ранг равный k.
По отношению к первым интегралам СДУ справедливо следующее
утверждение.
Утверждение 2.1. Для СДУ (2.41) порядка n, удовлетворяющей усло-
виям существования и единственности решений (2.48), (2.49) или (2.48),
(2.50), существует не более
1
−
n
независимых первых интегралов.
Другими словами, если для некоторой СДУ, скажем, 3-го порядка,
построено, например, 4 первых интеграла, то два из них всегда являются
