Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.


41
ji
λ≠λ
,
j
i
≠
,
nji ,1,
=
, (2.18)
то
0det
≠
W
, и существует матрица
},,{diag
~
21
1
n
AWWA λλλ==
−
K
,
которая является диагональной. Остальные матрицы преобразованной
системы вычисляются по формулам (2.10), (2.13), (2.14) при
WP
=
. Ре-
зультирующая система уравнений (2.8), (2.12) называется ка но ни че-
ской ди агона льн ой фо рмо й.
Пример 2.1. Привести к диагональной форме систему
,
56
10
xx
−−
=
&
и найти её решение при
T
x ]32[
0
=
.
Решение. В данном случае полином
65
56
1
det)det()(
2
+λ+λ=
+λ
−λ
=−λ=λ AEA
.
Корни уравнения
065
2
=+λ+λ
равны
2
1
−=λ
,
3
2
−=λ
, то есть усло-
вие
ji
λ
≠
λ
(2.18) удовлетворяется. Поэтому в качестве матрицы при-
ведения можно использовать матрицу Вандермонда (2.17), которая в дан-
ном случае имеет вид
−−
=
32
11
W
.
По формуле (2.6) или (2.7) находим
−−
−==
−
12
13
det
1
1
Wadj
W
W
.
Полагая
xWx
~
=
, по (2.9) при
WP
=
получим
42
−
−
=
−−
−−
−−
==
−
30
02
32
11
56
10
12
13
~
1
AWWA
.
Следовательно, заданная система в канонической диагональной форме
имеет вид
xx
−
−
=
30
02
~
&
или
.
~
3
~
,
~
2
~
22
11
xx
xx
−=
−=
&
&
При этом
]79[
~
0
1
0
−==
−
xWx
. Решение последней системы легко
записать сразу:
tt
ee
xtx
22
101
9
~
)(
~
−−
==
,
tt
ee
xtx
33
201
7
~
)(
~
−−
−==
,
и найти решение
)(tx
исходной системы по формуле
)(
~
)( txWtx
=
.
Имеем
+−
+−
=
−
−−
=
−−
−−
−
−
tt
tt
t
t
ee
ee
e
e
tx
32
23
3
2
2118
97
7
9
32
11
)(
.
Таким образом, приведение однородной системы дифференциаль-
ных уравнений к диагональной форме позволяет легко найти её решение.
Если матрица А системы (2.1) имеет форму, отличную от сопровождаю-
щей, но различные собственные числа, то способ приведения системы к
канонической диагональной форме состоит в том, что одним преобразо-
ванием подобия матрица системы сначала приводится к сопровождаю-
щей форме, а затем другим – к диагональной форме. Соответствующие
формулы приводятся ниже.
Приведение уравнений системы к канонической управляемой
форме. Рассмотрим систему с одним входом и одним выходом
,
bg
Ax
x
+
=
&
(2.19)
gxcy
T
β+=
. (2.20)
43
Необходимо выбрать матрицу преобразования
у
P
такую, чтобы за-
мена
xPx
у
~
=
привела систему (2.19), (2.20) к к ано ниче ской уп рав -
ляе мо й ф ор ме , т.е. к виду
,
~
~
~
~
gbxAx +=
&
(2.21)
,
~
~
gxcy
T
β+=
(2.22)
где
A
~
– сопровождающая матрица (2.15), а вектор
b
~
имеет вид
.
1
0
0
0
~
=
M
b
(2.23)
Заметим сразу, что систему (2.19), (2.20) можно привести к канони-
ческой управляемой форме только при условии [8, 9]:
0det
≠
U
,
][
1
bAAbbU
n−
= K
, (2.24)
где
xn dim
=
. При этом матрица преобразования подобия
у
P
опреде-
ляется по формуле
UMP
y
=
, (2.25)
в которой матрица
М
имеет вид
.
0001
001
00
01
1
1
32
121
−
−
α
αα
α
α
α
=
L
L
M
L
L
NM
n
n
M
(2.26)
Здесь
i
α
– коэффициенты полинома
)det()( AEA
−
λ
=
λ
(2.16).
Пример 2.2. Привести к канонической управляемой форме систему
44
gxx
+
=
1
1
12
31
&
,
xy ]21[=
.
Решение. Так как
2
=
n
, то по (2.24)
][ ABbU
=
. Тогда
,
3
4
1
1
12
31
==Ab
=
31
41
U
.
Определитель
0
1
det
≠
−
=
U
, следовательно, приведение воз-
можно. Характеристический полином матрицы A заданной системы
52
12
31
det)(
2
−λ−λ=
−λ−
−−λ
=λA
.
Его коэффициенты
5
0
−=α
,
2
1
−=α
. Поэтому по (2.26) матрица
−
=
01
12
M
.
Найдем матрицу преобразования
у
P
по формуле (2.25)
.
21
11
,1det,
11
12
01
12
31
41
1
−
−
===
−
=
−
yyy
PPP
Далее по формулам преобразования подобия (2.9), (2.10), (2.13) при
y
PP =
находим
=
−
−
=
−
−
==
−
25
10
11
12
13
21
12
31
21
11
~
1
yyy
PAPPA
,
=
−
−
==
−
1
0
1
1
21
11
~
1
bPb
y
,
]34[
11
12
]21[
~
=
==
y
TT
Pcc
.
45
Итак, в новых переменных состояния уравнения заданной системы
имеют вид
gxx
+
=
1
0
~
25
10
~
&
,
xy
~
]34[
=
,
что соответствует выражениям (2.15) и (2.21) – (2.23) при
2
=
n
и
0
=
β
.
Приведение уравнений системы к канонической наблюдаемой
форме. Для этой цели необходимо найти такую матрицу преобразования
н
P
, чтобы преобразование подобия (2.3) при
н
PP =
приводило систему
(2.19), (2.20) к ка но нич ес кой набл юдае мо й фо рм е, т.е. к виду
(2.21), (2.22), где
α−
α−
α−
α−
=
−1
2
1
0
100
010
001
000
~
n
A
K
MMOMM
K
K
K
,
.
1
0
0
0
~
=
M
c
(2.27)
Это приведение возможно, если
0det
≠
N
, где
=
−1
2
nT
T
T
T
Ac
Ac
Ac
c
N
M
. (2.28)
Соответствующая матрица преобразования подобия находится по
формуле
1
)(
−
= MNP
н
, (2.29)
причем матрица M по-прежнему определяется по формуле (2.26).
Пример 2.3. Привести к канонической наблюдаемой форме систему
gxx
+
=
1
3
21
32
&
,
xy
]12[
=
.
46
Решение. Так как
2
=
n
, то по второй формуле (2.28) находим
]85[
21
32
]12[ =
=Aс
T
,
=
85
12
N
.
Поскольку
011det
≠
=
N
, то приведение возможно. Воспользовав-
шись формулами (2.16), (2.26) и (2.29), получим
,14
21
32
det)(
2
+λ−λ=
−λ−
−
−
λ
=λ
A
1
0
=α
,
4
1
−=α
,
−
=
01
14
M
,
−
==
−
12
43
1
MNP
н
,
11det
1
−=
−
н
P
,
−−
−
−=
32
41
11
1
н
P
.
Затем по формулам преобразования подобия (2.9), (2.10) и (2.13) при
н
PP
=
получим
−
=
−
−
==
−
41
10
32
41
21
32
12
43
11
1
~
1
нн
APPA
,
−
=
−
==
−
7
5
1
3
12
43
~
1
bPb
н
,
[ ] [ ]
10
32
41
12
11
1
~
=
−
==
н
TT
Pcc
.
Итак, по (2.21) и (2.22) в новых переменных состояния заданная сис-
тема имеет вид
gxx
−
+
−
=
7
5
~
41
10
~
&
,
xy
~
]10[=
.
Матрица A и вектор c полученных уравнений по форме, очевидно,
соответствуют матрице
A
~
и вектору
c
~
из (2.27) при
2
=
n
. Следова-
47
тельно, уравнения системы приведены к заданной канонической наблю-
даемой форме.
Структурные схемы канонических форм уравнений динамиче-
ских систем. В этом случае соответствующая структурная схема системы
имеет минимальное число не равных нулю коэффициентов матриц и век-
торов системы по сравнению с другими формами. Поэтому эти формы
очень удобны для моделирования динамических систем и исследования
влияния различных воздействий и изменения параметров систем на свой-
ства их движений. Это моделирование осуществляется с помощью ЭВМ
или специальных комплексов, где все ненулевые коэффициенты струк-
турной схемы системы должны набираться и настраиваться. Поэтому чем
меньше ненулевых коэффициентов в уравнениях модели, тем она проще,
и тем проще её «набор», настройка и проведение исследования. Именно
поэтому канонические формы уравнений динамических систем и соот-
ветствующие им структурные схемы являются наиболее удобными фор-
мами для исследования свойств систем и зависимости этих свойств от
параметров системы и внешних воздействий.
Уравнения системы с двумя выходами
1
y
,
2
y
и одним входом g в
ка но ни чес кой уп ра вля емой фо рм е имеют вид
,
1
0
0
0
1000
0100
0010
1210
gxx
n
+
α−α−α−α−
=
−
M
K
K
M
K
K
&
MOMM
(2.30)
gdxcccy
n 1211
][ += K
, (2.31)
gdxqqqy
n 2212
][ += K
, (2.32)
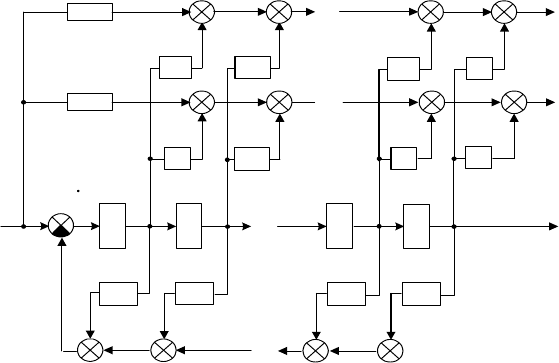
Структурная схема, соответствующая канонической управляемой
форме (2.30) – (2.32), приведена на рис. 2.1.
Уравнения систем с двумя входами
1
g
,
2
g
и одним выходом y в
ка но ни чес кой наб лю да ем ой фо рм е имеют вид
48
,
100
010
001
000
2
3
2
1
1
3
2
1
1
2
1
0
g
h
h
h
h
g
b
b
b
b
x
nnn
x
+
+
α−
α−
α−
α−
−
=
MM
K
MMOMM
K
K
K
&
(2.33)
2211
]1000[ gdgdxy ++= K
. (2.34)
...
...
...
...
g
x
n
x
n
x
n
-1
x
2
x
1
y
1
y
2
∫
∫ ∫
∫
α
n
-1
α
n-
2
α
1
α
0
с
n
с
n
-1
с
2
с
1
q
n
q
n-1
q
2
q
1
d
1
d
2
Рис. 2.1
Структурная схема, соответствующая этим уравнениям динамиче-
ской системы с двумя входами
1
g
,
2
g
и одним выходом y в канониче-
ской наблюдаемой форме, приведена на рис. 2.2.
На основе уравнений (2.30) – (2.34), а также рис. 2.1 и рис. 2.2 мож-
но сделать вывод, что каноническая управляемая форма более удобна для
моделирования систем с одним входом и несколькими выходами. В тоже
время, каноническая наблюдаемая форма является более удобной для
моделирования систем с несколькими входными воздействиями и одним
выходом.

49
Приведение уравнений системы к канонической диагональной
форме. Случай произвольной формы матрицы А. Вернемся снова к за-
даче приведения к канонической диагональной форме системы уравнений
(2.1), (2.2), где матрица А – произвольного вида, но с ра зличн ыми со б-
ств ен ным и чи сла ми . В этом случае в преобразовании подобия
xPx
~
2
=
матрицу преобразования
2
P
можно определить по формуле
UMWWPP
y
==
2
, (2.35)
где матрицы U и M находятся по формулам (2.24) и (2.26). Причем в дан-
ном случае вектор b в (2.24) может быть взят любым, важно лишь, чтобы
0det
≠
U
. Матрица W в (2.35) – это матрица Вандермонда, определяемая
выражением (2.17).
Как показано выше, преобразование подобия с матрицей
UM
при-
водит матрицу A к сопровождающей форме, а затем преобразование с
матрицей Вандермонда W (если
A
j
A
i
λ≠λ
) – к диагональной форме. Таким
образом, в результате преобразования
xPx
~
2
=
вектора переменных со-
стояния
x
в вектор переменных
x
~
система уравнений (2.1), (2.2) прини-
мает вид (2.8) и (2.12), где матрица
A
~
имеет диагональную форму.
§ 2.2. Общие свойства решений дифференциальных уравнений
Определение решения дифференциального уравнения. Как было
установлено выше, основной формой математических моделей динами-
ческих систем являются обыкновенные дифференциальные уравнения. В
общем случае такое уравнение можно записать в виде
∫
g
1
b
1
∫
...
α
0
α
1
x
2
x
1
b
2
b
3
h
2
h
1
...
...
h
3
g
2
...
∫
α
n-1
x
n
x
n
x
n-1
y
d
d
2
1
Рис. 2.2
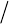
50
),,( gxtfx
=
&
, (2.36)
где
x
,
g
– некоторые функции времени t, т.е.
)(txx
=
,
)(tgg
=
;
dtdxx =
&
– производная функции
x
по t,
),,(
gxtf
– нелинейная функ-
ция своих аргументов t,
x
,
g
.
При этом
)(
tgg
=
– называется возмущающей функцией, а
)(
txx
=
– решением уравнения (2.36) [14, 15].
В некоторых случаях функция
0)(
=
tg
, тогда уравнение (2.36)
принимает вид
),(
xtfx
=
&
(2.37)
и называется однородным дифференциальным уравнением.
В отличие от него уравнение (2.36) называется неоднородным диф-
ференциальным уравнением.
Очень часто, как видно из приведенных выше примеров, для описа-
ния динамических систем одного уравнения (2.36) недостаточно. Тогда
рассматриваются системы из
n
дифференциальных уравнений (СДУ).
Например, при
2
=
n
и двух функциях
1
g
и
2
g
такая система имеет вид
),,,,(
212111
ggxxtfx =
&
,
),,,,(
212122
ggxxtfx =
&
. (2.38)
Для удобства СДУ записываются в векторной форме
),,( gxtfx
=
&
, (2.39)
Здесь
T
n
txtxtxtxx ])()()([)(
21
K==
,
T
n
tgtgtgtgg ])()()([)(
21
K==
–
векторные функции времени, а
L),,(),,([),,(
21
gxtfgxtfgxtf =
T
n
gxtf )],,(K
– нелинейная вектор-функция.
Величина
fxn dimdim
=
=
– называется порядком СДУ (2.39).
Для краткости эти факты записываются так
n
Rx∈
,
k
Rg ∈
,
n
Rf ∈
.
Здесь
n
R
– векторное пространство (П.3.1) размерности
n
, т.е. каждая
векторная функция принадлежит векторному пространству соответст-
вующей размерности и наоборот, каждое пространство «натянуто» на
множество векторов соответствующей размерности.
Аналогичный вид имеет однородная СДУ
