Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.


31
Это модель вход-выход рассматриваемого генератора, записанная с
помощью операторных передаточных функций.
Чтобы получить модель вход-выход генератора в виде дифференци-
альных уравнений, исключим из (1.33) оператор
dtdp /
=
. Для этого ум-
ножим обе его части на оператор
)1)(1(
вя
++ pTpT
.
В результате получим
.)1()1]()1([
)1)(1(
3в632в62я5
641вя
gpTkkgpTkkpTk
ukkkypTpT
++++++
+
=
+
+
Возвращаясь к исходным обозначениям переменных и вводя новые
обозначения для коэффициентов
н
Uy ∆→
,
в
Uu ∆→
,
ω∆→
3
g
,
н
2
Rg ∆→
,
и
kkkk
г
641
=
;
гн
625
kkkk =+
;
ω
=
г
63
kkk
будем иметь
+
∆
+++
∆
+
+∆=∆+
∆
++
∆
dt
Rd
TkkkTk
dt
Rd
TTk
UkU
dt
Ud
TT
dt
Ud
TT
и
н
в
625
я
5
2
н
2
вя
5
вгн
н
вя
2
н
2
вя
])([
)(
ω∆+
ω∆
+∆+
ωω гнвгнг
k
dt
d
TkRk
(1.35)
Выражение (1.35) – это дифференциальное уравнение вход-выход
генератора постоянного тока. Как видно, оно полностью соответствует
общей форме моделей вход-выход линейных систем с одним выходом и
тремя входами.
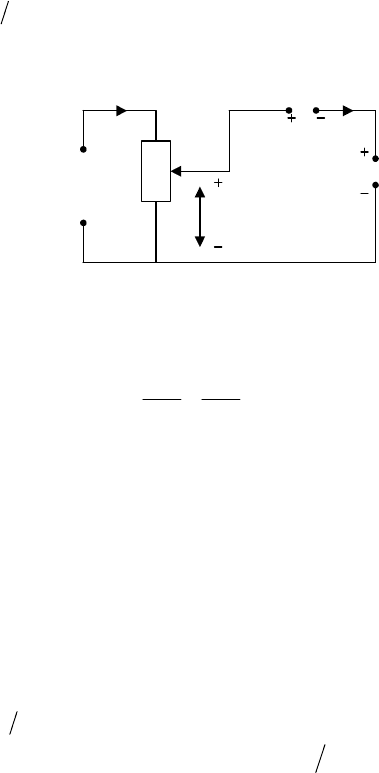
Модель потенциометра и входной цепи тиристорного усилителя.
Перейдем к построению модели потенциометра и входной цепи усилите-
ля, используя схему, приведенную на рис. 1.19.
Учитывая отсутствие индуктивности, уравнение цепи получим на
основе закона Ома. Полагая
0
=
у
I
ввиду его малости, можно записать
н
max
п
п
UU
ϕ
ϕ
=
.
Тогда
32
нппу
UkEUEU
этэт
−=−=
,
где
maxпп
ϕϕ=k
– коэффициент передачи потенциометра
п
R
;
п
ϕ
,
max
ϕ
– текущий и максимально возможный углы поворота оси потен-
циометра.
U
п
Е
эт
I
у
U
у
U
н
R
п
п
I
Рис. 1.19
п
I
Вводя отклонения переменных, получим из предыдущего равенства
∆−−∆−=+
н
0
нп
2
п
п
п
0
UUk
k
E
k
E
kUU
этэт
уу
,
где
maxпп
/
ϕϕ∆=∆k
, а
п
ϕ∆
– изменение положения оси потенциометра
п
R
, вызванное необходимостью изменения заданного значения напряже-
ния на нагрузке. Отсюда с учетом обозначения
н
Uy ∆=
выводим урав-
нение входной цепи усилителя в отклонениях
)(
1
пу
ygkU −=∆
, (1.36)
а также её уравнение в установившемся режиме
)(
0
н
0
п
0
н
UgkU −=
, (1.37)
где
п
0
kEg
эт
=
.
В данном случае величина
2
пп1
kEkg
эт
∆−=
является уставкой
или за даю щи м во зде йст ви ем , рассматриваемой САР ГПТ.
Из предыдущих выражений следует, что если исходные уравнения
каких-то элементов линейные, то уравнения установившихся режимов и
уравнения в отклонениях этих элементов будут тоже линейными и по
форме одинаковыми.
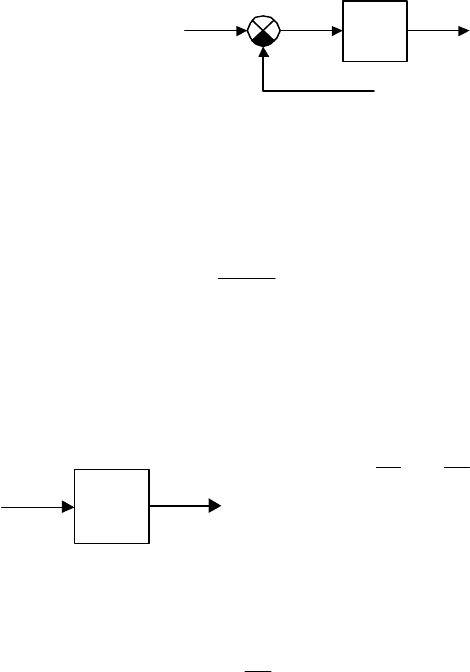
33
Структурная схема входной цепи тиристорного усилителя, соответ-
ствующая уравнению (1.36), приведена на рис. 1.20. В соответствии с
этим уравнением входная цепь усилителя является безынерционной, так
как в указанном уравнении не фигурируют постоянные времени.
k
П
∆U
у
y
g
1
Рис. 1.20
Модель тиристорного усилителя. Так как выходной переменной
тиристорного усилителя (рис. 1.21) является напряжение
в
U
, поступаю-
щее на обмотку возбуждения двигателя, то в первом приближении его
уравнение можно записать так
уув
в
у
UkU
dt
Ud
T ∆=∆+
∆
. (1.38)
Здесь
у
k
– коэффициент усиления,
у
T
– постоянная времени тиристор-
ного усилителя.
Для получения его уравнений в переменных состояния введем обо-
значение
3
в
xU
→∆
. Тогда из (1.38) вытекают равенства
=∆
∆+−=
,
,
1
3в
у33
xU
U
T
k
x
T
x
у
у
у
&
(1.39)
которые являются уравнениями в пере-
менных состояния усилителя.
Подставляя принятое выше обозначение
в
Uu ∆=
в уравнение
(1.38), получим модель тиристорного усилителя в форме вход-выход
ууу
Uku
dt
du
T ∆=+
.
Это уравнение с помощью передаточной функции усилителя можно
записать следующим образом
уу
)( UpWu ∆=
, (1.40)
∆U
у
ТУ
∆U
B
Рис. 1.21

34
где
1
)(
+
=
pT
k
pW
у
у
у
. (1.41)
В соответствии с уравнением (1.40) тиристорный усилитель можно
представить, как показано на рис. 1.22.
u
∆U
у
W
у
( p)
Рис. 1.22
Усилитель относится, очевидно, к динамическим элементам, по-
скольку в (1.41) фигурирует постоянная времени.
На основании полученных моделей элементов системы можно полу-
чить модель всей САР ГПТ.
Модель системы в переменных состояния. Модель системы полу-
чается путем объединения полученных выше моделей её элементов. По-
этому для наглядности выпишем здесь эти модели, т.е. уравнения (1.30),
(1.36) и (1.39)
+=
++−=
+−=
.
,
1
,
1
2625
3
я
3
2
я
2
2
я
1
я
4
2
в
1
1
в
1
xкgкy
g
Т
к
g
Т
к
x
T
x
Т
к
x
u
Т
к
x
T
x
&
&
)(
1пу
ygkU −=∆
=
∆+−=
.
,
1
3
у33
xu
U
T
k
x
T
x
у
у
у
&
Далее образуем вектор-столбец из переменных состояния моделей
элементов системы

35
=
3
2
1
x
x
x
x
с
.
Используя уравнения выходов моделей (1.30), (1.36) и (1.39), преоб-
разуем выражения для производных
1
x
&
,
2
x
&
и
3
x
&
так, чтобы они зависели
только от входных воздействий системы
1
g
,
2
g
,
3
g
и переменных со-
стояния
1
x
,
2
x
и
3
x
. В результате будем иметь
,
1
в
1
1
в
1
u
Т
к
x
T
x +−=
&
,
1
3
я
3
2
я
2
2
я
1
я
4
2
g
Т
k
g
Т
k
x
T
x
Т
k
x ++−=
&
),(
1
26251
п
у
у
3
у
3
xkgkgk
Т
k
x
T
x −−+−=
&
2625
xkgky
+
=
. (1.42)
При выводе уравнений (1.42) были исключены промежуточные пе-
ременные y, u и
у
U∆
, в соответствии с третьим уравнением (1.30), урав-
нением (1.36) и вторым уравнением (1.39).
Уравнения (1.42), вводя соответствующие обозначения, можно запи-
сать в матричной форме уравнений в переменных состояния
,
ccсcс
gBxAx +=
&
(1.43)
c
T
cс
T
c
gdxcy +=
. (1.44)
Здесь
−−
−
−
=
yy
6
пy
яя
4
в
1
в
1
0
0
1
0
1
ТТ
kkk
ТТ
k
Т
k
Т
А
с
,
=
3
2
1
g
g
g
g
c
,

36
=
0
0
000
y
5пy
y
пy
я
3
я
2
Т
kkk
Т
kk
Т
k
Т
k
B
c
,
=
0
0
6
kс
с
,
[
]
00
5
kd
T
c
=
.
Таким образом, уравнения САР ГПТ в переменных состояния (1.43),
(1.44) совпадают с общей формой уравнений в переменных состояния
динамических систем. На основе полученных уравнений можно также
заключить, что рассмотренная система имеет третий порядок, три входа,
один выход. Элементы матриц
с
А
,
c
B
и векторов
c
c
,
c
d
также опреде-
ляются параметрами элементов системы: коэффициентами передач
i
k
и
постоянными времени
в
T
,
я
Т
,
у
Т
.
Модель системы в форме вход-выход. Для построения этой моде-
ли объединяются уравнения вход-выход всех элементов системы. Это
уравнения (1.34), (1.36) и (1.40). Выпишем их здесь
3
г
2
гнг
)()()( gpWgpWupWy
и ω
++=
,
)(
1
п
y
ygkU −=∆
,
yy
)( UpWu ∆=
.
В этих уравнениях необходимо оставить только входные g
1
, g
2
, g
3
и
выходную величину системы y, а остальные переменные u,
y
U∆
исклю-
чить. Выполняя это последовательно, будем иметь
)()(
1
п
y
ygkpWu −=
,
3
г
2
гн
1
п
y
г
)()()()()( gpWgpWygkpWpWy
и
ω
++−=
,
или окончательно
3г2гн1пyгпyг
)()()()())()(1( gpWgpWgkpWpWykpWpW
ии ω
++=+
, (1.45)
Уравнение (1.45) является уравнением вход-выход рассматриваемой
САР ГПТ в операторной форме. Для перехода в нем к временной форме,
необходимо подставить в (1.45) выражения для передаточных функций,

37
освободиться от знаменателя в левой и правой части, поставить операто-
ры перед переменными, а затем перейти к функциям и их производным.
Полученное в результате уравнение будет неоднородным линейным
дифференциальным уравнением третьего порядка с тремя возбуждаю-
щими функциями, то есть тоже будет соответствовать общей форме мо-
делей вход-выход динамических систем.
Далее для исследования свойств рассматриваемой САР ГПТ, в соот-
ветствии с системным подходом, необходимо найти решения уравнений
модели исследуемой системы. Перейдем к рассмотрению соответствую-
щих методов.

38
Г л а в а 2
РЕШЕНИЕ УРАВНЕНИЙ ДИНАМИЧЕСКИХ СИСТЕМ
§ 2.1. Канонические формы моделей в переменных состояния
Преобразование подобия. Процесс решения уравнений в перемен-
ных состояния динамических систем зависит от вида матрицы А из урав-
нения состояний. В общем случае эти уравнения имеют вид
BgAxx
+
=
&
, (2.1)
DgCxy
+
=
. (2.2)
Решением этой системы являются векторы
)(tx
и
)(ty
, при этом
)(tx
должен обращать уравнение (2.1) в тождество, причем
0
0
)( xtx =
,
где
0
x
– заданный вектор начальных условий.
Для облегчения решения или же для исследования свойств решения
система (2.1), (2.2) часто подвергается преобразованию подобия. Преоб-
разование подобия заключается в замене вектора состояния по формуле
xPx
~
=
(2.3)
при условии, что
0det
≠
P
. (2.4)
Здесь
x
~
– новый вектор состояния. Если (2.4) выполняется, то существу-
ет обратная матрица
1−
P
такая, что
E
P
P
=
−1
. (2.5)
Матрица
1−
P
вычисляется (см. П.1.20) по формуле
,adj
det
1
1
P
P
P =
−
(2.6)
где
Padj
– присоединенная матрица.
Из (2.5) и (2.6) следует, что
PEPP detadj
=
. Присоединенную
матрицу можно вычислить по формуле
])1[(
T
ij
ji
PPadj
+
−=
,

39
где
T
ij
P
– алгебраическое дополнение (П.1.20) элемента матрицы
T
P
, стоя-
щего на пересечении i–й строки и j–го столбца.
Если n=2, то обратную матрицу можно записать непосредственно по
матрице Р, так как
=
2221
1211
pp
pp
P
,
−
−
=
−
1121
1222
1
det
1
pp
pp
P
P
. (2.7)
Чтобы найти уравнения преобразованной системы, продифференци-
руем равенство (2.3) по времени
x
P
x
&
&
~
=
и подставим в (2.1) с учетом
(2.3). В результате получим
BgxAPxP
+=
~
~
&
,
а после умножения на
1−
P
слева, найдем
.
~
~
~
~
gBxAx +=
&
(2.8)
Здесь введены обозначения
AP
P
A
1
~
−
=
, (2.9)
B
P
B
1
~
−
=
. (2.10)
Аналогично, подставляя (2.3) в (2.2), будем иметь
DgxCPy
+
=
~
(2.11)
или
gDxCy
~
~
~
+=
, (2.12)
где обозначено
CPC
=
~
, (2.13)
D
D
=
~
. (2.14)
Выражения (2.8) и (2.12) – это уравнения той же динамической сис-
темы (2.1), (2.2), но в новых переменных состояния.
Удобство преобразования подобия (2.3) в том, что выбором матрицы
P систему (2.1), (2.2) можно привести к каноническому виду, в котором
матрица
A
~
имеет простую форму (много нулей и мало чисел). С другой
стороны, полагая
xPx
1
~
=
, где
1
1
−
= PP
, можно по тем же формулам
40
(2.9), (2.10) и (2.13), (2.14) при
1
PP =
вернуться к исходному вектору
переменных состояния x. Наибольшее распространение получили преоб-
разования подобия, приводящие матрицу
A
~
в (2.8) к следующим фор-
мам [12]:
- диагональной,
- сопровождающей,
- транспонированной сопровождающей.
Приведение к канонической диагональной форме. Допустим,
матрица А в системе (2.1) имеет соп ро во жда ющ ую форму, то есть
.
1000
0100
0010
1210
−
α−α−α−α−
=
n
A
K
K
M
K
K
MOMM
(2.15)
Характеристический полином этой матрицы всегда имеет вид
nn
n
AEA λ+λα++λα+α=−λ=λ
−
−
1
110
)det()( K
. (2.16)
Как видно, коэффициенты полинома
)(
λ
A
, взятые с обратным зна-
ком, являются коэффициентами последней строки сопровождающей мат-
рицы данного полинома. Именно поэтому она так и называется.
Если в системе (2.1) матрица А является сопровождающей, и корни
вычисленного по формуле (2.16) полинома
)
(
λ
A
различные, то для
приведения системы (2.1) к канонической диагональной форме в качестве
матрицы преобразования можно взять матрицу Вандермонда.
Обозначим
n
λλλ K,,
21
– корни полинома (2.16). Тогда матрица
−−−−
λλλλ
λλλλ
λλλλ
=
11
3
1
2
1
1
22
3
2
2
2
1
321
1111
n
n
nnn
n
n
W
K
M
K
K
K
MOMM
. (2.17)
является матрицей Вандермонда.
Если выполняется условие (2.15) и неравенства
