Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.

21
++=++++ )()(),()(
1
)(
11100
)(
01
2
2
3
3
1
pgpbbypMpy)apapap(a
pBpA
434214444 34444 21
),()()(),(
2022
)(
2
222120101
2
gpNpgpbpbbgpN
pB
+++++
444 3444 21
. (1.23)
Здесь
),(
0
ypM
,
),(
101
gpN
,
),(
202
gpN
– полиномы от p, коэффициен-
ты которых определяются начальными условиями;
0
y
,
10
g
,
20
g
– век-
торы начальных условий для функций
)(ty
,
)(
1
tg
,
)(
2
tg
, то есть (в дан-
ном случае)
=
20
10
00
0
y
y
y
y
&&
&
;
=
20
20
20
g
g
g
&
;
[
]
1010
gg =
.
Определение передаточной функции. П ер ед ато чн ой фун кци-
ей системы по некоторому входному воздействию называется отношение
изображения по Лапласу ее выходной величины к изображению этого
входного воздействия при нулевых начальных условиях и нулевых ос-
тальных воздействиях.
Например, передаточные функции системы, описываемой уравне-
нием (1.14), определяются выражениями
нну
pg
py
pW
)(
)(
)(
1
1
=
,
нну
pg
py
pW
)(
)(
)(
2
2
=
. (1.24)
Здесь сокращение нну – условное обозначение нулевых начальных усло-
вий и нулевых других воздействий, приложенных к данной системе.
В соответствии с приведённым определением из (1.23) с учетом обо-
значений (1.24) следуют формулы
)(
)(
)(
1
1
pA
pB
pW =
,
)(
)(
)(
2
2
pA
pB
pW =
. (1.25)
Отметим, что формулы (1.25) по форме совпадают с выражениями
(1.18), (1.19). Отличие состоит лишь в том, что в (1.25)
p
– комплексная
переменная, а в (1.18), (1.19)
p
– оператор, т.е. в выражениях (1.18),
(1.19)
dtdp /
=
.

22
Из уравнения (1.23) динамической системы (1.14) с учетом равенств
(1.25) при нулевых начальных условиях получаем уравнение вход-выход
этой системы
)()()()()(
2211
pgpWpgpWpy +=
, (1.26)
записанное с использованием передаточных функций.
Уравнение (1.26) является алгебраическим уравнением. Оно позво-
ляет при необходимости восстановить полиномы
),(
0
ypM
,
),(
01
gpN
,
),(
02
gpN
и далее, используя правила обратного преобразования Лапла-
са, найти функцию
)(ty
, т. е. решение обыкновенного дифференциаль-
ного уравнения (1.14) как при нулевых, так и при ненулевых начальных
условиях.
Обычно задание математических моделей вход-выход динамических
систем и их элементов осуществляется именно в форме передаточных
функций типа (1.25) и соответствующих структурных схем, аналогичных
показанной на рис. 1.14.
§ 1.3. Аналитический метод построения моделей
Описание динамических систем. Получить математические моде-
ли реальных динамических систем можно на основе известных законов
природы, описывающих процессы, протекающие в исследуемой системе.
С этой целью обычно рассматривается принципиальная (обобщен-
ная) схема системы и анализируется ее работа. В системе выделяются
отдельные функционально обособленные элементы, и система представ-
ляется совокупностью этих элементов и связей между ними. То есть со-
ставляется функц ион аль на я сх ема системы. На этой же схеме отме-
чаются промежуточные переменные, и указываются внешние воздейст-
вия, действующие на эту систему. Функциональная схема позволяет раз-
бить составление модели системы на ряд последовательных этапов.
Рассмотрим эту процедуру моделирования (получения математиче-
ских моделей) на примере системы автоматического регулирования на-
пряжения генератора постоянного тока (САР ГПТ).
Схема САР ГПТ показана на рис. 1.15. На этом рисунке обозначено:
ТУ – тиристорный усилитель,
п
R
– потенциометр,
эт
Е
– высокоста-
бильный источник эталонной ЭДС,
п
U
– напряжение, снимаемое с по-
тенциометра, ГПТ – генератор постоянного тока,
н
R
– сопротивление
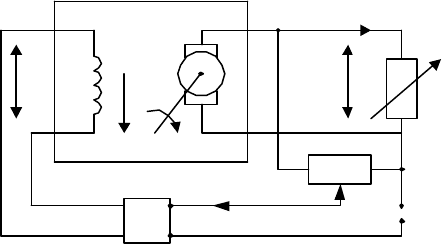
23
нагрузки генератора, переменное по величине,
н
U
– напряжение на на-
грузке.
Функционирование системы регулирования достаточно ясно из при-
веденной схемы, поэтому на нем останавливаться не будем.
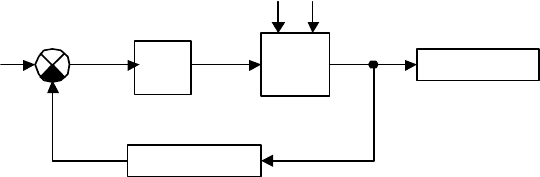
Перейдем к рассмотрению функциональной схемы. Эта схема пока-
зана на рис. 1.16, где обозначены основные функциональные элементы
САР ГПТ: генератор, нагрузка -
н
R
, потенциометр
п
R
, тиристорный
усилитель (ТУ), а также переменные
в
U
,
н
U
,
п
U
,
х
U
и воздействия
эm
E
,
я
ω
. Здесь
я
ω
- скорость вращения якоря генератора внешним
двигателем.
U
H
U
B
OB
Ф
B
I
Т У
U
У
E
Э Т
R
П
R
Н
I
Н
ГПТ
ω
я
U
П
Т У
Рис.1.15
Для получения модели системы необходимо найти математическую
модель каждого элемента, а затем объединить эти модели в одну систему
уравнений.
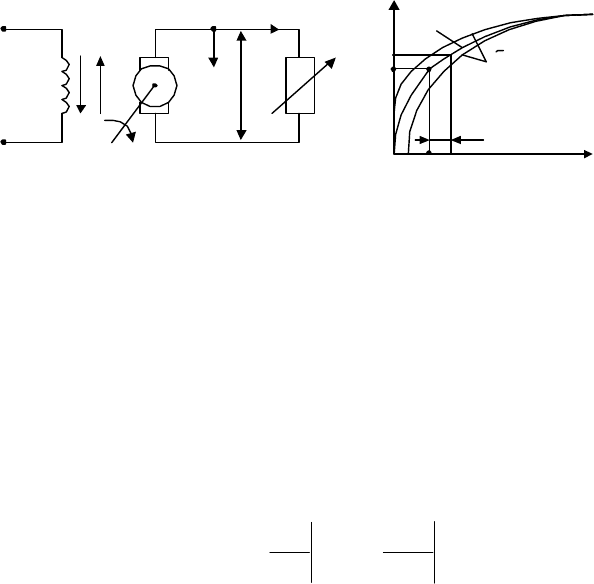
Вывод моделей элементов начнем с ГПТ. Для этой цели построим на
рис. 1.17,а более подробную схему генератора.
Основными процессами в генераторе являются электромагнитные
процессы, которые определяются законами Кирхгофа и Ленца. Эти зако-
ны связывают значения электрических напряжений
в
U
,
н
U
, токов
в
I
,
н
I
магнитных потоков
в
Ф
,
я
Ф
и скорость изменения последних.
Чтобы упростить модель примем следующие допущения:
1. Ток через потенциометр пренебрежительно мал, т.е.
0
п
≈I
.
2. Реакция якоря пренебрежимо мала, т.е.
вяв
~
~
ФФФ ≈+
.
24
Зависимость магнитного потока
в
~
Ф
от тока возбуждения
в
I
имеет
вид, показанный на рис. 1.17,б, т.е. эта зависимость является нелинейной
и неоднозначной. Говорят, что эта зависимость имеет “гистерез ис”.
Однако в первом приближении гистерезисом обычно пренебрегают, за-
меняя реальные кривые “средней” кривой
в
Ф
.
Т У
Г П Т Нагрузка
E
ЭТ
U
П
U
B
U
H
R
Н
Потенциометр
ω
Я
Рис. 1.16
В результате уравнения ГПТ, схема которого показана на рис. 1. 17,а,
принимают вид
)(
вввввв
IФwRIU
&
+=
,
)(
ввяяг
I
ФС
E ω=
,
)()(
няянянг
I
Ф
wRRIE
&
++=
,
ннн
RIU =
.
Здесь
в
w
,
я
w
– коэффициенты пропорциональности между скоростью
изменения магнитного потока и ЭДС самоиндукции, возникающей в об-
мотке возбуждения и в якорной обмотке;
)(
вв
IФ
,
)(
яя
I
Φ
– усредненные
нелинейные функции, описывающие зависимости магнитных потоков
возбуждения и якоря от соответствующих токов,
я
С
– конструктивная
постоянная генератора,
г
E
– ЭДС, возникающая в якорной обмотке ге-
нератора.
Таким образом, полученные уравнения ГПТ являются нелинейными.
Чтобы упростить задачу дальнейшего анализа, эти уравнения, прежде
всего, линеаризуют.
Линеаризация моделей. Линеаризация нелинейных моделей обыч-
но осуществляется в окрестности установившихся значений переменных
системы. У стано вив шиеся зна че ни я – это значения переменных,
25
которые устанавливаются в системе при постоянных значениях внешних
воздействий, когда
∞
→
t
. Обычно в качестве установившихся значений
принимают номинальные значения переменных и обозначают их с помо-
щью нулевого индекса. Например,
0
в
U
,
0
в
I
– установившиеся значения
напряжения и тока возбуждения
в
U
и
в
I
.
Ф
I
∆
I
I
Н
U
H
I
П
ω
я
w
я
Ф
Я
Ф
в
w
в
R
в
U
в
R
я
Н
R
Ф
0
I
0
в
в
в
в
в
Ф
В
Ф
В
а) б)
Рис. 1.17
Линеаризация осуществляется путем разложения нелинейных функ-
ций в ряды Тейлора в окрестности установившихся значений и отбрасы-
вания слагаемых, содержащих вторые, третьи и т. д. степени отклонений
переменных от их установившихся значений.
С этой целью, прежде всего, вводятся отклонения переменных сис-
темы от их установившихся значений, т.е. полагают
в
0
вв
0
ввв
UUUUUU
∆+=→−=∆
,
в
0
вв
0
ввв
IIIIII
∆+=→−=∆
и так далее.
Разлагая в ряд Тейлора зависимость
)(
вв
IФ
в окрестности
0
в
I
, получим
K
321
321
+∆+∆+=∆+
′
2
2
в
в
2
в
в
в
0
ввв
0
вв
0
в
0
в
0
в
0
в
2
)()(
в
I
Ф
I
Ф
I
dI
Фd
I
dI
dФ
IФIIФ
При линеаризации предполагается, что отклонения переменных
очень малы. Следовательно, слагаемые, содержащие отклонения во вто-
рой, в третьей и в более высоких степенях, пренебрежимо малы по срав-
нению с первыми двумя слагаемыми. Поэтому, отбрасывая в разложении
слагаемые, содержащие вторую, третью и т.д. степени отклонения
в
I
∆
,
получим (приближенное) равенство
26
в
0
в
0
вв
0
вв
)( IФФIIФ ∆
′
+=∆+
,
которое описывает линеаризованную зависимость магнитного потока от
тока возбуждения.
Аналогично можно получить зависимость
н
0
я
0
ян
0
ня
)( IФФIIФ ∆
′
+=∆+
.
Перепишем теперь нелинейные уравнения ГПТ с учетом линеаризо-
ванных нелинейностей и переменных в отклонениях
в
0
вввв
0
вв
0
в
)( IФwRIIUU
&
∆
′
+∆+=∆−
,
,))((
))((
0
яян
0
нян
0
н
в
0
в
0
в
0
яя
н
IФwRRRII
IФФС
&
∆
′
+∆++∆+=
=∆
′
+ω∆+ω
(1.27)
))(()(
н
0
нн
0
нн
0
н
RRIIUU ∆+∆+=∆+
.
Полученная система (1.27) является уравнениями генератора в от-
клонениях. Эта система содержит уравнения как установившихся, так и
переходных режимов. Чтобы получить из (1.27) уравнения установивше-
гося режима, необходимо все отклонения и их производные положить
равными нулю. В результате будем иметь
0
в
0
в
0
в
RIU =
,
0
н
0
ня
0
в
0
яя
)( IRRФС +=ω
, (1.28)
0
н
0
н
0
н
RIU =
.
Это уравнения установившегося режима ГПТ. Они определяют
связь между установившимися значениями переменных этого объекта и,
по-прежнему, являются нелинейными.
Для получения уравнений переходных режимов генератора, необхо-
димо из (1.27) вычесть соответствующие уравнения (1.28), и, кроме того,
пренебречь бесконечно малыми величинами второго порядка. В резуль-
тате получим уравнения
в
0
ввввв
IФwRIU
&
∆
′
+∆=∆
,

27
,)(
0
яян
0
нн
0
ня
в
0
в
0
яя
0
вя
н
IФwRIIRR
IФСФС
&
∆
′
+∆+∆+=
=∆
′
ω+ω∆
(1.29)
н
0
нн
0
нн
IRRIU ∆+∆=∆
.
Эти уравнения являются линейными. Они описывают связи между
отклонениями переменных генератора, а не между самими переменными,
и называются:
- уравнения ГПТ в отклонениях,
- уравнения первого приближения ГПТ,
- линейные уравнения ГПТ,
- линейная модель ГПТ.
Модель ГПТ в переменных состояния. Для
получения уравнений ГПТ в переменных состояния
введем следующие обозначения. Выберем в качестве
переменных состояния
в
I∆
и
н
I∆
потому, что
именно они стоят под знаком производной в системе
(1.29), т.е. положим
в1
Ix ∆=
,
н2
Ix ∆=
. Обозначим
также входные и выходные величины, показанные на
рис. 1.18, т.е. положим
в
Uu ∆=
,
н2
Rg ∆=
,
,
3
ω∆=g
н
Uy ∆=
.
С учетом введенных обозначений систему (1.29) можно записать
следующим образом:
u
R
xx
R
Фw
в
11
в
0
вв
1
=+
′
&
,
1
я
0
н
0
в
0
яя
3
я
0
н
0
вя
2
я
0
н
0
н
22
я
0
н
0
яя
)(
x
RR
ФC
g
RR
ФC
g
RR
I
xx
RR
Фw
+
′
ω
+
+
+
+
−=+
+
′
&
,
2
0
н2
0
н
xRgIy +=
.
Величины
в
0
вв
R
Фw
′
и
я
0
н
0
яя
RR
Фw
+
′
имеют размерность времени (секунды),
поэтому они называются п ос тоя нн ым и вр ем ени и обозначаются так
в
в
0
вв
Т
R
Фw
=
′
– постоянная времени цепи возбуждения,
ГПТ
R
ω
U
U
∆
∆
∆
∆
н
н
в
Рис. 1.18

28
я
я
0
н
0
яя
)(
Т
RR
Фw
=
+
′
– постоянная времени цепи якоря.
Постоянные времени всегда характеризуют инерционные свойства
соответствующего элемента системы. Чем больше постоянная времени,
тем медленнее происходят изменения в данном элементе.
Все остальные множители в правых частях приведенных уравнений
являются коэ ффи ци ент ами пер едач и. Они определяют соотноше-
ния между величинами в установившемся режиме, то есть при отсутст-
вии изменений переменных.
Выделив в предыдущей системе производные и разделив на посто-
янные времени левые и правые части этих уравнений, получим коорди-
натную форму записи уравнений ГПТ в переменных состояния
+=
++−=
+−=
.
,
1
,
1
2625
3
я
3
2
я
2
2
я
1
я
4
2
в
1
1
в
1
xкgкy
g
Т
к
g
Т
к
x
T
x
Т
к
x
u
Т
к
x
T
x
&
&
(1.30)
Для записи системы уравнений (1.30) в матричной форме, введем
следующие обозначения:
,
2
1
=
x
x
x
][
1
0
1
яя
4
в
ij
a
TT
k
T
A =
−
−
=
,
=
6
0
k
c
,
[
]
00
5
kb =
,
=
я
3
я
2
в
1
0
00
T
k
T
k
T
k
В
,
=
3
2
g
g
u
g
, (1.31)
Тогда уравнения (1.30) примут вид
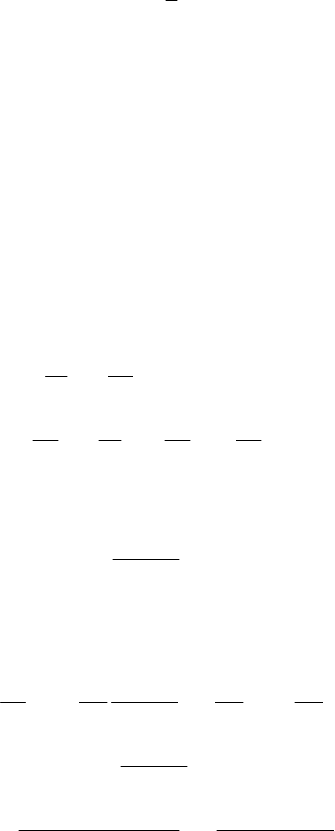
29
+=
+=
.
,
gbxcy
BgAxx
T
&
(1.32)
Из равенств (1.31) видно, что все элементы матриц модели (1.32)
ГПТ определяются его параметрами – постоянными времени
в
Т
и
я
Т
и
коэффициентами передачи
61
kk −
.
Модель ГПТ в уравнениях вход-выход. Вывод этих уравнений не-
сколько отличается от предыдущих. Поскольку уравнения вход-выход
должны отразить только связи между входными и выходными величина-
ми ГПТ (см. рис. 1.18), то из уравнений (1.29) необходимо, прежде всего,
исключить отклонения
в
I∆
,
я
I∆
и их производные
в
I
&
∆
и
я
I
&
∆
или, что
то же самое, из уравнений (1.30) исключить
2121
, , ,
xxxx
&&
.
Для упрощения записи применим операторную форму. Тогда из пер-
вых двух уравнений (1.30) получим
.
1
,
1
3
я
3
2
я
2
2
я
1
я
4
2
в
1
1
в
1
g
Т
k
g
Т
k
x
T
x
Т
k
px
u
Т
k
x
T
px
++−=
+−=
Чтобы исключить
1
x
, сначала выразим его из первого уравнения
u
pT
k
x
1
в
1
1
+
=
.
Приводя подобные члены во втором уравнении и подставляя выра-
жение для
1
x
, получим
,
1
)
1
(
3
я
3
2
я
2
в
1
я
4
2
я
g
Т
k
g
Т
k
u
pT
k
Т
k
x
T
p ++
+
=+
,
1
)1(
3322
в
1
42
я
gkgku
pT
k
kxpT ++
+
=+
)1()1)(1(
я
3322
яв
41
2
+
+
+
++
=
pT
gkgk
u
pTpT
kk
x
.

30
Далее, подставляя
2
x
в последнее уравнение системы (1.30), будем
иметь
)1(
)(
)1)(1(
я
33226
яв
41
625
+
+
+
++
+=
pT
gkgkk
u
pTpT
kk
kgky
или
3
я
63
2
я
26я5
яв
641
)1()1(
)1(
)1)(1(
g
pT
kk
g
pT
kkpTk
u
pTpT
kkk
y
+
+
+
+
+
+
++
=
. (1.33)
Уравнение (1.33) – искомое уравнение вход-выход ГПТ в оператор-
ной форме.
Введем некоторые обозначения
01
2
2
10
г
яв
641
)(
)1)(1(
α+α+α
β
==
++
pp
pW
pTpT
kkk
u
,
где
64110
kkk=β
,
1
0
=α
,
яв1
TT +=α
,
вя2
TT=α
.
Аналогично
2021
2021
гн
я
26я5
)(
)1(
)1(
α+α
β+β
==
+
++
p
p
pW
pT
kkpTk
,
где
я521
Tk=β
,
62520
kkk +=β
,
я21
Т
=
α
,
1
20
=
α
.
3031
30
г
я
63
)(
1 α+α
β
==
+
ω
p
pW
pT
kk
где
6330
kk=β
,
я31
T=α
,
1
30
=α
.
В приведённых обозначениях
)(
гu
pW
– операторная передаточная
функция ГПТ по напряжению возбуждения,
)(
г
pW
ω
– операторная пере-
даточная функция ГПТ по скорости якоря,
)(
гн
pW
– операторная переда-
точная функция ГПТ по нагрузке.
Из этих выражений видно, что коэффициенты
i
α
и
ji
β
передаточ-
ных функций генератора также определяются только его параметрами
я
T
,
в
T
,
61
kk −
.
С учетом введенных обозначений уравнение (1.33) можно записать так
3г2гнгu
)()()( gpWgpWupWy
ω
++=
. (1.34)
