Gasch R., Twele J. (Eds.) Wind Power Plants: Fundamentals, Design, Construction and Operation

Подождите немного. Документ загружается.

402 12.1 Methods to manipulate the drive drain

Within the individual fields of operation, e.g. zone 1, normal wind (4 to 12 m/s),

the control and the controller loops work autonomously. Nevertheless, the current

status has to be reported continuously to the supervisory system, since only this

system can decide if the set control values are still valid or whether it is necessary

to shift to a different mode of operation by a maneuver. A considerably simplified

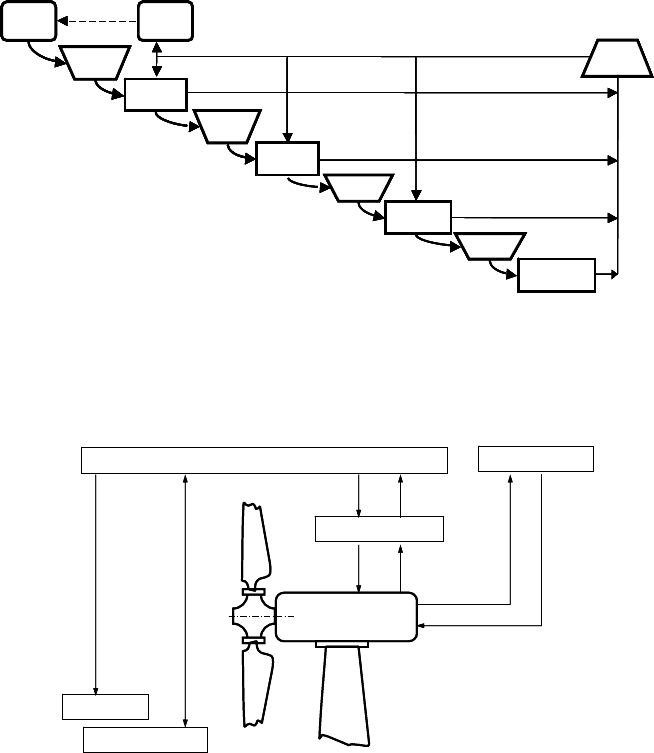
flow chart of the supervisory system is shown in Fig. 12-3.

In the hierarchy of systems, given in Fig. 12-4, the supervisory system is above

the control systems.

Start

Maschine

O.K.?

Stillstand

Gehe zu

Start

in den

Betrieb I

Teillast

Betrieb II

Vollast

Trudel-

betrieb

Gehe

zurück zu

StopStart

Machine

O.K.?

Stand still

Go to

Start

Operation I

Part. load

Operation

Full load

Idling

back to

StopStart

Maschine

O.K.?

Stillstand

Gehe zu

Start

in den

Betrieb I

Teillast

Betrieb II

Vollast

Trudel-

betrieb

Gehe

zurück zu

StopStart

Machine

O.K.?

Stand still

Go to

Start

Operation I

Part. load

Operation

Full load

Idling

back to

Stop

Fig. 12-3 Simplified flow chart of the supervisory system, variable-speed wind turbine

Monitoring

Supervisory System

Control Systems

Safety System

Remote Control

Monitoring

Supervisory System

Control Systems

Safety System

Remote Control

Fig. 12-4 Hierarchy of the systems

12 Supervisory and control systems for wind turbines 403

Phases

Supervisory system

Pitch control Yaw control Generator

excitation

Converter control

J ȕ



gen

wind

Anemometer

Speed Pitch

angle

Yaw

angle

External

information

grid

Wind

Generator

:,M

Converter

Transformer

Direction

Phases

Supervisory system

Pitch control Yaw control Generator

excitation

Converter control

J ȕ



gen

wind

Anemometer

Speed Pitch

angle

Yaw

angle

External

information

grid

Wind

Generator

:,M

Converter

Transformer

Phases

Supervisory system

Pitch control Yaw control Generator

excitation

Converter control

J ȕ



gen

wind

Anemometer

Speed Pitch

angle

Yaw

angle

External

information

grid

Wind

Generator

:,M

Converter

Transformer

Direction

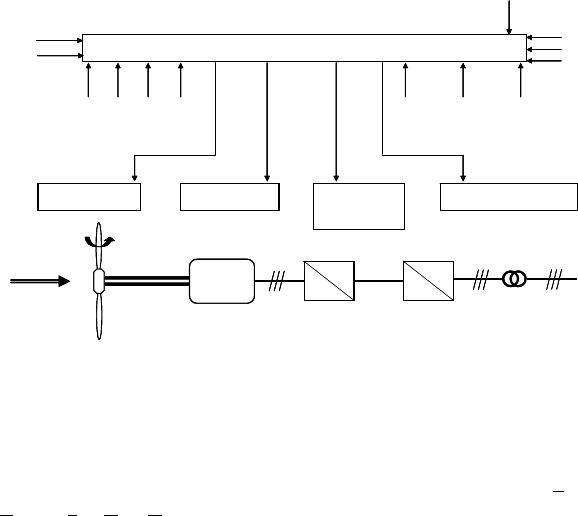
Fig. 12-5 Supervisory system - controllers - scheme of drive train with converter

Fig. 12-5 shows the most important controllers of a variable-speed wind turbine

and the necessary sensor information.

The supervisory system governs also the SCADA system (SCADA = Supervi-

sory Control and Data Acquisition) which consists of the monitoring and remote

control modules. The monitoring module collects operational data (e.g. perform-

ance data and faults, etc.) and delivers required information “outwards”, e.g. to the

wind farm management office. The data transfer is either continuous or upon

demand, e.g. via modem. The monitoring module cannot intervene in the turbine

operation, therefore “it has no responsibility”. The remote control serves e.g. to

turn the wind turbine on and off from the wind farm management office or to reset

the control after having checked and cleared a minor fault. For some machines,

even control parameters or operating modes (e.g. noise reduced operation) can be

set via the remote control.

The safety system has the responsibility for safe operation. It acts at once and

directly if severe malfunctions occur, e.g.

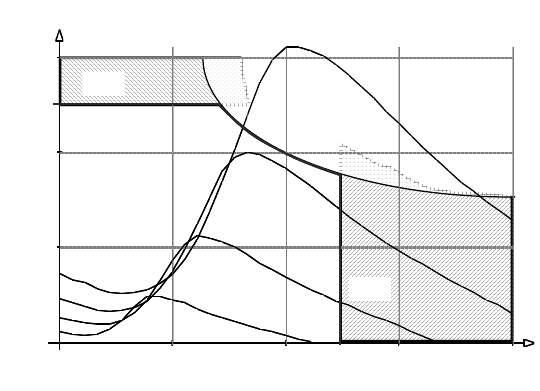
- Excessive rotational speed (overspeed), Fig. 12-6 or

- Excessive power or torque,

- Differences among the pitch angles of the blades

- Excessive vibrations (unbalance, icing on the blades)

- Manual emergency shut-down, etc.

The safety system must assure that the wind turbine at no time damages or de-

stroys itself. If a malfunction occurs it has to shut down the wind turbine fast and

reliably and disengage it.

Therefore, this system has to be simple and robust (preferably hardware-based),

and redundant in the most important components (e.g. two independent braking

systems) and be of fail-safe design. In case of failures in the electronics or hydraulics

404 12.1 Methods to manipulate the drive drain

the system has to bring the turbine into a safe state automatically and without use

of external energy (e.g. braking to standstill). This has to be assured anytime, dur-

ing any operating state or maneuver.

[Nm]

100 200 300 4000

100

4 m/s

6 m/s

10 m/s

8 m/s

max

Speed n in rpm

Torque M in Nm

[Nm]

100 200 300 4000

100

4 m/s

6 m/s

10 m/s

8 m/s

max

Speed n in rpm

Torque M in Nm

Fig. 12-6 Operating range limits for rotational speed, torque and power of a small wind turbine

D = 4 m (see Figs. 6-8 and 6-9)

12.1 Methods to manipulate the drive drain

Basically, the drive train can be influenced either through aerodynamics at the ro-

tor side, or by load manipulation, i.e. at the generator side (mechanical load side).

The wind turbine produces torque and thrust depending on the wind speed and

the angle of attack of the blade sections, cf. chapters 5 and 6. The angle of attack

itself depends on the rotational speed, the pitch angle and also on the yaw angle

between rotor axis and wind. The driving torque feeds the mechanical load. If the

driving torque is larger than the load torque the positive torque difference acceler-

ates the drive train, Fig. 12-7.

For a quantitative consideration of the control processes the inertia of the drive

train (and rotor) has to be considered, for larger wind turbines also the torsional-

vibrations behavior. The build-up of aerodynamic forces at the blades (Wagner-

Küssner’ functions) is usually so rapid, that the blade performance characteristics,

which were derived with the assumption of stationary behavior, can be used - see

annex II of this chapter.

12 Supervisory and control systems for wind turbines 405

Turbine

M = M (, v, )

( ) )

Driving

torque M

Blade pitch J

-M

Wind

(t)

T = T

Load torque

Thrust T

ǻM

Angular

speed

Inertia Ĭ

Wind turbine with…

low tip speed ratio | high tip speed ratio

Yaw angle ȕ

Rotor-Wind

, v,

)

': dt

Turbine

M = M (, v, )

( ) )

Driving

torque M

Blade pitch J

-M

Wind

(t)

T = T

Load torque

Thrust T

ǻM

Angular

speed

Inertia Ĭ

Wind turbine with…

low tip speed ratio | high tip speed ratio

Yaw angle ȕ

Rotor-Wind

, v,

)

': dt

Fig. 12-7. Controlling the drive train of a wind turbine via aerodynamics and electrical load

12.1.1 Aerodynamic manipulation measures

The following are simple methods to reduce the power extraction of the rotor dur-

ing strong winds:

- Turning the rotor out of the wind (Western mill),

- Holding the rotational speed constant in order to provoke flow separation

at the blades during strong winds,

- Deploying spoilers or brake flaps.

A more elegant method is the pitching of the blades which will be discussed later.

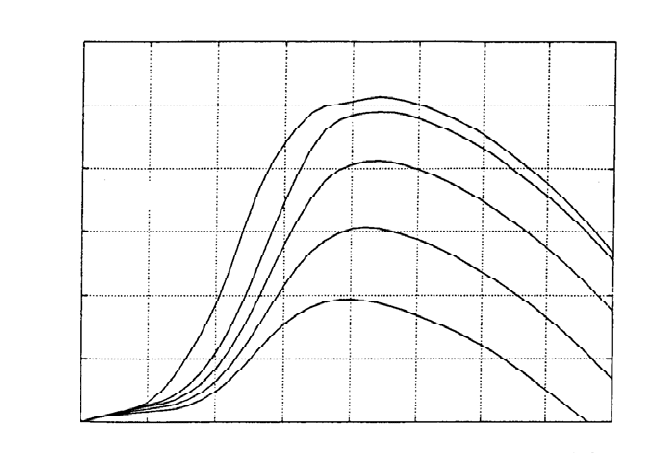
Fig. 12-8 shows the effects of turning the rotor out of the wind (i.e. producing

oblique flow) on the power characteristics of a small wind turbine with a high de-

sign tip speed ratio for strong winds. This is similar to the principle of the Western

mill. With increasingly oblique flow, the maximum of the power curve decreases,

but the corresponding rotational speed remains nearly constant.

If the rotational speed is kept constant for strong winds, the circumferential com-

ponent in the velocity triangles does not change, Fig. 12-9. This can be used to

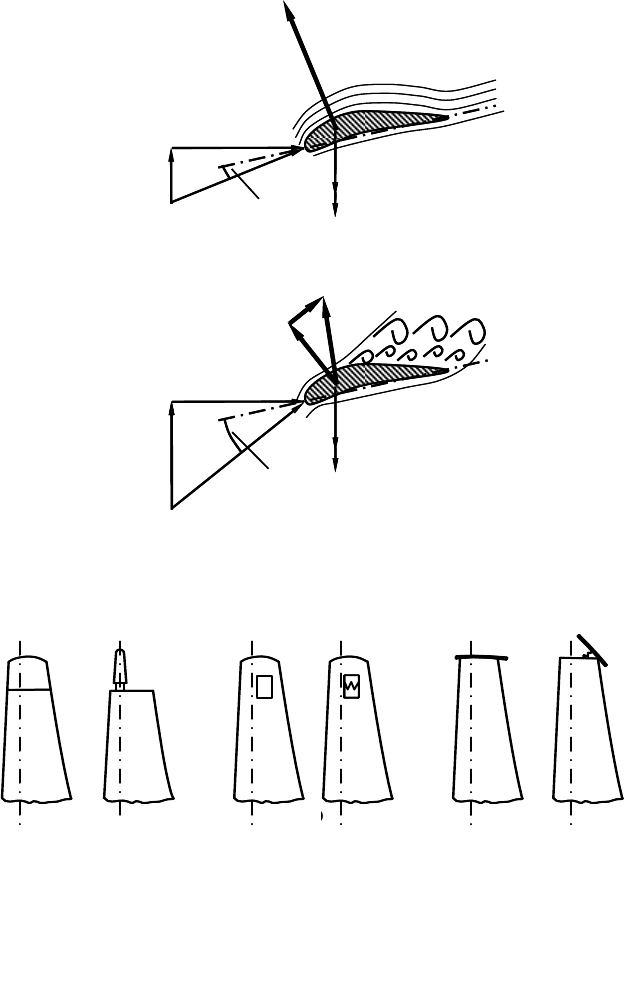
limit aerodynamically the power extraction of the wind turbine, as already discov-

ered in the 1950s by Johannes Juul, the ingenious inventor of the “Danish con-

cept”. The angle of attack

increases with stronger winds so much that the flow

separates (stall effect). Thus, the drag grows strongly and rotates the resulting

force R to point more downwind, Fig. 12-9. With a sophisticated blade design it is

possible to keep its circumferential component in the strong wind zone nearly con-

stant – and therefore the power as well since the rotational speed is already fixed.

The “Danish concept” was turned into practice by Juul using an induction (i.e.

asynchronous) generator which has its rotational speed more or less rigidly tied to

the three-phase grid frequency (50 or 60 Hz). This turns out to be a load control

utilizing cleverly the effect of flow separation.

406 12.1 Methods to manipulate the drive drain

n in rpm

0 50 100 150 200 250 300 350 400

P in kW

0°

20°

30°

50°

40°

v = 10 m/s

n in rpm

0 50 100 150 200 250 300 350 400

P in kW

0°

20°

30°

50°

40°

v = 10 m/s

n in rpm

0 50 100 150 200 250 300 350 400

P in kW

0°

20°

30°

50°

40°

v = 10 m/s

Fig. 12-8 Effect of turning the rotor out of the wind on the power characteristics of a turbine

with a high tip speed ratio (angle between rotor and wind, see fig. 12-19 and 12-1)

Flaps and spoilers are aerodynamic brakes which protect against overspeed or

serve as a simple means to limit and control power. They are activated by aero-

dynamic or centrifugal forces or are forced by a hydraulic control.

The braking torque M

from a flap areas A

can be easily estimated given the

assumption that they are located at the outer radius R, and using the simplification

that relative velocity equals circumferential speed

R. The braking torque M

the flaps is then obtained by equating it to the driving torque M

of the rotor,

= M

, since our goal is to assure that the rotor does not speed up to load-free

idling

(Ȝ) A

R ȡ/2 = c

D.fl



U

/2 , (12.1)

where A

is the rotor swept area resp. A

the flap area. The drag coefficient c

D.fl

is mostly equal to that of a rectangular plate and is in the range between 1.2 to 2.0

depending on the aspect ratio. c

(Ȝ) is the torque moment coefficient of the rotor.

Equation (12.1) may be transformed into the dimensionless equation

(Ȝ) = c

M.fl

(Ȝ) . (12.2)

12 Supervisory and control systems for wind turbines 407

A.stall

u = const

2.stall

u = const

2.opt

A.opt

Normal wind

Strong wind

A.stall

u = const

2.stall

u = const

2.opt

A.opt

Normal wind

Strong wind

Fig. 12-9 Triangles of velocity at design point and under strong wind conditions: flow separa-

tion (stall effect) due to constant rotational speed and resulting reduction of lift and increase of

drag

a) b) c)a) b) c)

Fig. 12-10 Different types of braking flaps a) turnable blade tip, b) braking flap in the blade sur-

face, c) fold-out end disk

The flap torque moment coefficient c

M.fl

(Ȝ) is

M.fl

= c

D.fl

/ A

Ł f · O

. (12.3)

The factor f is determined by the ratio of flap area to rotor area.

408 12.1 Methods to manipulate the drive drain

0 2 4 6 8 Ȝ 10

0.12

0.1

0.08

0.06

0.04

0.02

, c

1/500

1/250

1/200

1/150

1/100

f = 1/50

0 2 4 6 8 Ȝ 10

0.12

0.1

0.08

0.06

0.04

0.02

, c

1/500

1/250

1/200

1/150

1/100

f = 1/50

Fig. 12-11 Operating points on c

(

-curve of the rotor depending on the flap size;

parameter f = c

D.flap

· A

flap

rotor

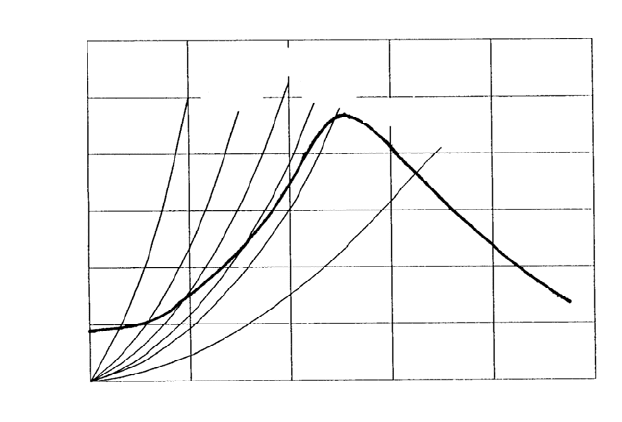
After plotting the curve c

M.fl

(

) =

f into the c

-O diagram, Fig. 12-11, the in-

tersection of this curve and c

(

) gives the operating point of the system ‘wind

turbine with deployed flaps. Turbines with a high tip speed ratio require only

small flap areas: for a wind turbine with a design tip speed ratio of

= 7, the

idling tip speed ratio would be reduced from

idle

= 13 to approximately 6.5, pro-

vided that the area of the deployed flaps is 1/500 of the rotor area. In contrast to

that, turbines with a low tip speed ratio require very large flap areas: a spoiler

brake is not suitable for this.

The most elegant and accurate method of aerodynamically influencing the rotor

is provided by a blade pitching system. There are two alternatives to be distin-

guished:

- Reducing the angle of attack

(pitching to feather, i.e. nose into

the wind, resp. trailing edge out of the wind) by increasing the blade

pitch angle

, Fig. 12-12, and

- Increasing the angle of attack

(pitch to stall, i.e. nose out of the

wind, resp. trailing edge into the wind) by reducing the blade pitch

angle

, Figs. 12-13.

If at constant wind speed, Fig. 12-12 top, the pitch angle is increased, the angle of

attack at a blade section is reduced from the point of optimum flow conditions to

smaller angles of attack. Therefore, the lift is reduced - and consequently the

power output since the driving circumferential component of the lift, which wants

to accelerate the rotor, gets smaller. In Fig. 12-12, bottom, the influence of the

blade pitch angle on the power coefficient curve c

(

) is shown. The rotor char-

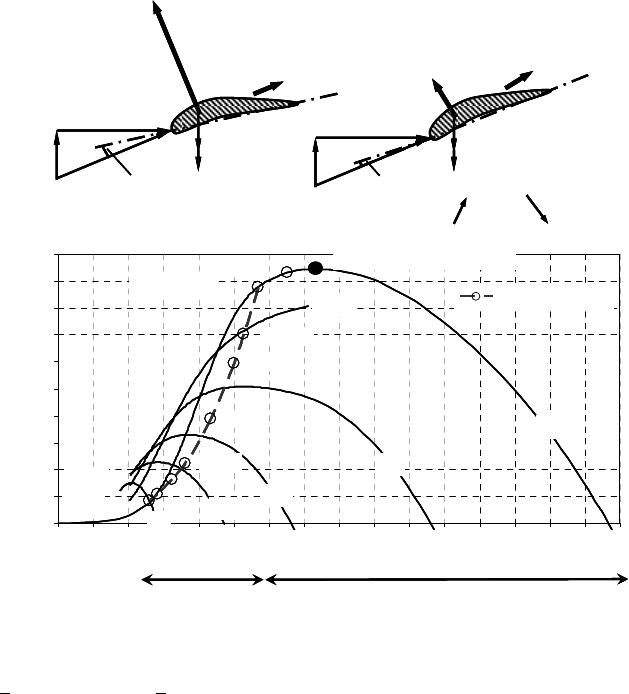
12 Supervisory and control systems for wind turbines 409

acteristics of a wind turbine with a high design tip speed ratio for various pitch

angles are given in the Figs. 6-15 to 6-17.

Pitch control systems which operate with a reduction of the angle of attack

(pitch to feather) to smaller values have a good accuracy and produce a smoothly

running rotor since for all occurring angles the flow remains attached to the blade.

The disadvantage is that in the range od strong winds the pitch angle will require

relatively large changes, see Fig. 12-14.

u = ˖r

A.D

u = ˖r

< D

A.D

Pitch to feather:

J => D

Normal operation, zone 1

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

0,5

012345678910111213141516

Tip speed ratio



Power coefficient c

Operating points

Zone 2

Zone 1

= 5

= 0

10 m/s

4- 9 m/s (

opt

)

25 m/s

= 11,4 m/s

13 m/s

12,3 m/s

18 m/s

23 m/s

20 m/s

15 m/s

u = ˖r

A.D

u = ˖r

< D

A.D

Pitch to feather:

J => D

Normal operation, zone 1

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

0,5

012345678910111213141516

Tip speed ratio



Power coefficient c

Operating points

Zone 2

Zone 1

= 5

= 0

10 m/s

4- 9 m/s (

opt

)

25 m/s

= 11,4 m/s

13 m/s

12,3 m/s

18 m/s

23 m/s

20 m/s

15 m/s

u = ˖r

A.D

u = ˖r

< D

A.D

Pitch to feather:

J => D

Normal operation, zone 1

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

0,5

012345678910111213141516

Tip speed ratio



Power coefficient c

Operating points

Zone 2

Zone 1

= 5

= 0

10 m/s

4- 9 m/s (

opt

)

25 m/s

= 11,4 m/s

13 m/s

12,3 m/s

18 m/s

23 m/s

20 m/s

15 m/s

Fig. 12-12 Control by pitching to feather, top: reduction of angle of attack D

by increasing the

pitch angle

; bottom: corresponding power characteristic c

(

) for blade angle

= 0° in zone 1

(v <

11,4 m/s) and 0° <

< 25° for zone 2 (11,4 m/s < v < 25 m/s), see fig. 12-2

410 12.1 Methods to manipulate the drive drain

A.D

> D

A.D

Pitch to stall:

dL < dL

dD>dD

J => D

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

0,5

012345678910111213141516

Schnelllaufzahl [-]

aerodyn. Leistungsbeiwert Cp [-]

- 1

- 2

- 3

- 4

Betriebspunkte

10 m/s

5 m/s

8 m/s

6 m/s

13,7 m/s

nenn

= 11,4 m/s

13 m/s

12,3 m/s

18 m/s

23 m/s

20 m/s

15 m/s

= 0

= - 4

Zone 2 Zone 1

Operating points

Tip speed ratio

Power coefficient c

Normal operation, zone 1

A.D

> D

A.D

Pitch to stall:

dL < dL

dD>dD

J => D

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

0,5

012345678910111213141516

Schnelllaufzahl [-]

aerodyn. Leistungsbeiwert Cp [-]

- 1

- 2

- 3

- 4

Betriebspunkte

10 m/s

5 m/s

8 m/s

6 m/s

13,7 m/s

nenn

= 11,4 m/s

13 m/s

12,3 m/s

18 m/s

23 m/s

20 m/s

15 m/s

= 0

= - 4

Zone 2 Zone 1

Operating points

Tip speed ratio

Power coefficient c

Normal operation, zone 1

A.D

> D

A.D

Pitch to stall:

dL < dL

dD>dD

J => D

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

0,5

012345678910111213141516

Schnelllaufzahl [-]

aerodyn. Leistungsbeiwert Cp [-]

- 1

- 2

- 3

- 4

Betriebspunkte

10 m/s

5 m/s

8 m/s

6 m/s

13,7 m/s

nenn

= 11,4 m/s

13 m/s

12,3 m/s

18 m/s

23 m/s

20 m/s

15 m/s

= 0

= - 4

Zone 2 Zone 1

Operating points

Tip speed ratio

Power coefficient c

Normal operation, zone 1

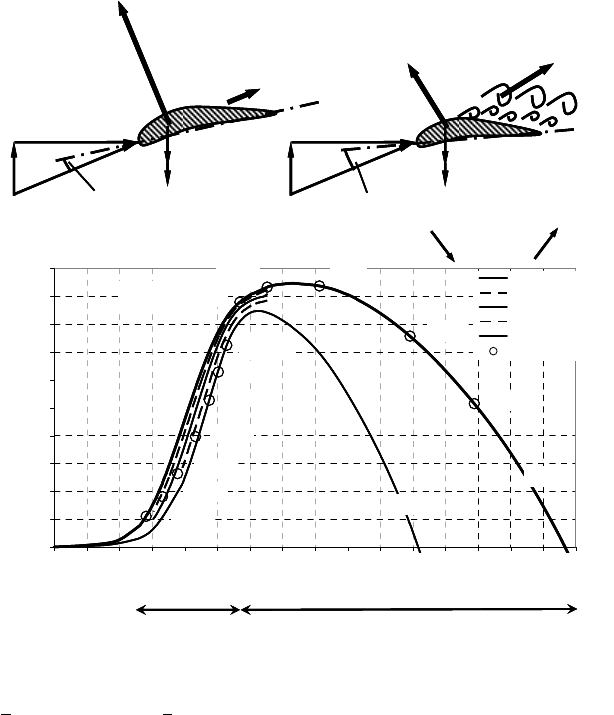
Fig. 12-13 Active-stall control, top: increase of angle of attack

(stall effect) by reducing the

pitch angle

; bottom: corresponding power characteristic c

(

) for blade angle

= 0° in zone 1

(v <

11,4 m/s) and -4° <

< 0° for zone 2 (11,4 m/s < v < 25 m/s)

Increasing the angle of attack (active stall, nose out of the wind) leads to a reduc-

tion of the power output as well, since the flow will separate from the blade,

which reduces the lift (a little) and increases the drag significantly, Fig. 12-13.

Provoking flow separation requires only small pitch angle changes and even

achieving a controlled rotor standstill is easy. But the thrust remains quite large for

this type of pitch control.

Fig. 12-14 compares the required pitch angle for constant power control in the

range of strong winds (11.4 to 25 m/s). Obviously, the stall-controlled wind tur-

bine requires only very small changes of the pitch angle to keep the power output,

which was originally slightly rippled, really constant.

The summary of the different ways to influence the rotor by blade pitching in

Table 12.1 gives an overview of the possibilities for wind turbine rotor operation.

Practical examples exist for each field in this table.

12 Supervisory and control systems for wind turbines 411

-5

4 6 8 1012141618202224

Windgeschwindigkeit [m/s]

Blattwinkel [°]

Pitchen in Fahnenstellung

Pitchen in den Abriss (Active-Stall)

Wind speed

Pitch angle [rr]

Pitch to feather

Pitch to stall (Active stall)

-5

4 6 8 1012141618202224

Windgeschwindigkeit [m/s]

Blattwinkel [°]

Pitchen in Fahnenstellung

Pitchen in den Abriss (Active-Stall)

Wind speed

Pitch angle [rr]

Pitch to feather

Pitch to stall (Active stall)

Fig. 12-14 Blade angle pitching to feather or to active stall in order to limit the power to rated

power P

for strong winds (v > v

= 11.4 m/s )

Table 12.1 Overview of possibilities for wind turbine rotor operation

Blade angle pitching

none To feather To stall

constant

e.g. wind turbines

of the classical

“Danish concept “

e.g. early MW wind

turbines

„active stall“

wind turbines

Rotor speed

variable

e.g. battery chargers

modern variable-

speed wind turbines

with A.C.-D.C.-A.C.

converter

At present not a

common wind

turbine concept

12.1.2 Drive train manipulation using the load

In chapter 10 on wind pump systems we already discussed how the differences in

the speed-torque characteristics of piston pumps and centrifugal pumps influence

the behavior of the total system. Moreover, from chapter 11 we know several

methods of drive train manipulation through the generator. They are briefly sum-

marized here: