Gasch R., Twele J. (Eds.) Wind Power Plants: Fundamentals, Design, Construction and Operation

Подождите немного. Документ загружается.

8.2 Free and forced vibrations of wind turbines - examples and phenomenology

292

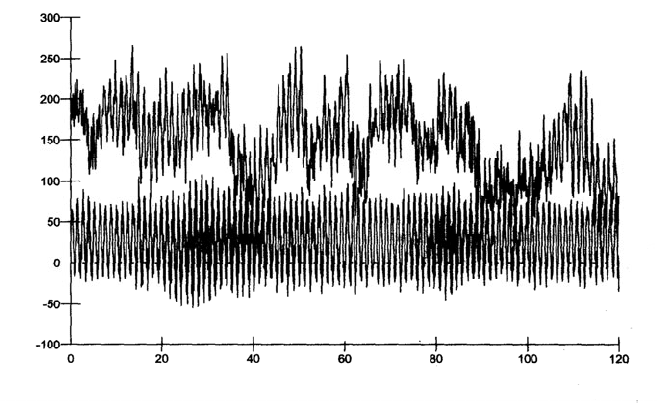
energy strongly excites the first flapwise natural frequency of the blade. The

response of the edgewise bending moment is shown as well. It is more narrow-

banded and is above all dominated by the alternating bending with the rotational

frequency induced by the blade weight. Here, the gustiness of the wind has only a

small influence.

Flapwise bending

Edgewise bending

Time in s

Bending moment at the root of the blade in kNm

Flapwise bending

Edgewise bending

Time in s

Bending moment at the root of the blade in kNm

Fig. 8-16 Simulated response of the flapwise and edgewise bending moment at the blade root

due to stochastic excitation by the wind, wind turbine of 500 kW

8.2.3 Drive train vibrations

In essence, the excitations of the vibrations in the drive train stem from:

- the blade passage: number of blades times the rotational frequency and its

harmonics,

- the turbulent wind field,

- the vertical wind profile for one- and two-bladed wind turbines,

- action of the control, blade pitching, torque moment changes in the

generator,

- teeth contact frequencies,

- etc..

The sufficient treatment of the dynamics of torsion of smaller wind turbines

(D < 50 m) is possible by modelling the drive train as a system with 2 or 3 degrees

of freedom (DOF), Fig. 8-17 left and middle. However, magnetic forces act

between rotor and stator of the generator which may be modelled for a synchronous

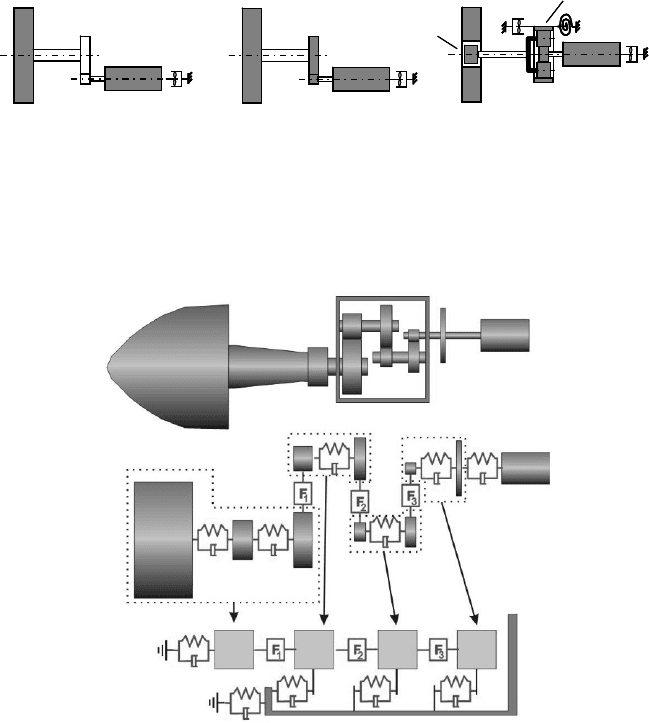
8 Structural dynamics

293

generator a as load dependent torsional spring. The forces for an asynchronous

generator, which has a slip to the grid frequency, may be described by a torsional

damper, as shown in Fig. 8-17, where the damping coefficient results from the

slope of the torque characteristic at the synchronous frequency, cf. chapter 11. For

large wind turbines the first edgewise eigenmode of the blades has to be consid-

ered in the dynamics of torsion and the fact that the casing of the gearbox is

mounted on the nacelle frame in elastic rubber bushings. Thus, one more degree of

freedom comes into play, and the drive train has four degrees of freedom - possi-

bly even five if individual inertia is assigned to the gear wheels in the model, Fig.

8-17, right.

Rotor

Gen

Gear

2 DOF

3 DOF

Hub

3Blade

Housing

5 DOF

Rotor

Gen

Gear

2 DOF

3 DOF

Hub

3Blade

Housing

5 DOF

Fig. 8-17 Modelling of the torsional drive train dynamics with different numbers of degrees of

freedom (in grey: moment of inertia Ĭ; torsional stiffnesses c

, c

, etc.; spring and damping

systems from the gearbox housing and generator)

Fig. 8-18 Modelling of the drive train dynamics as a multi-body system [10]

8.2 Free and forced vibrations of wind turbines - examples and phenomenology

294

Recent studies on the three-dimensional situation of the loading at the hub and in

the entire drive train as well as the damages observed in reality with larger wind

turbines show clearly the limitations and the inadequacies of the models described

above. As a result, multi-body-system models are being developed. Fig. 8-18

shows a model with torsional and translational degrees of freedom [10]. These

investigations become very complex if the gaps between the teeth flanks and,

moreover, the elasticities of the support provided by the nacelle frame and the

tower are considered.

The drive train is only slightly damped from the mechanical and aerodynamic

side. The edgewise movement of the blades merely provides an aerodynamic tor-

sional damping (see below). Only the elastic rubber support of the casing has a

positive effect – if a suitable rubber material is chosen. Fortunately, in modern

variable-speed wind turbines stability problems of the drive train may be avoided

by introducing torsional damping artificially via the generator: the air gap

moments can be varied by the fast electrical torque control of the generator.

8.2.4 Sub-models - overall system

For dynamic investigations at an early design stage it is advisable to cut the over-

all system of a wind turbine into suitably selected sub-systems, e.g.

- The tower-nacelle system with rigid blades

- The blade rigidly clamped at the root

- The drive train (dynamics of torsion), etc.

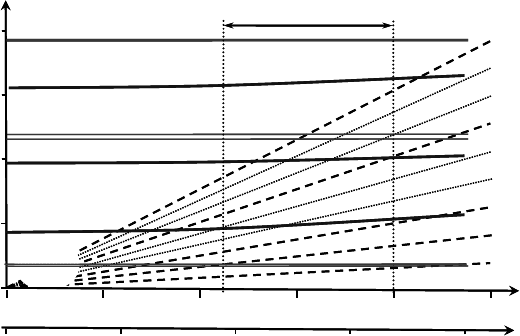
Drawing the natural frequencies of the sub-systems in their dependency on the

rotational speed in one single Campbell diagram, Fig. 8-19, allows us not only to

detect potential resonance problems but also to judge the danger of interference of

natural frequencies which lie close together.

Changes in the natural frequencies also occur if eigenmodes of the sub-systems

influence one another. The example of the drive train dynamics shows that espe-

cially for large wind turbines the simplified consideration of the blades as rigid

bodies is inadmissible. Here, the blade’s first edgewise natural frequency is that

low that it falls into the range of the drive train’s first torsional natural frequency

at which the rotor of the turbine oscillates against the generator. Thus a coupling is

formed: blade and drive train dynamics are married inseparably together. Some

vibration modes are even influenced by the tower dynamics. Therefore, the natural

frequencies determined for the sub-systems are shifted in the assembled overall

system.

8 Structural dynamics

295

Operating range

510 1520 25

Rotational speed

in rpm

Tower

bending

Flapw.

bending

Edgewise

bending

Tower torsion

Flapwise bending

Tower bending

Longitudinal

Lateral

Natural and rotational

frequency in Hz

1ȍ

2ȍ

3ȍ

4ȍ

5ȍ

6ȍ

7ȍ

8ȍ

9ȍ

0.1 0.2 0.3 0.4

in Hz

Operating range

510 1520 25

Rotational speed

in rpm

Tower

bending

Flapw.

bending

Edgewise

bending

Tower torsion

Flapwise bending

Tower bending

Longitudinal

Lateral

Natural and rotational

frequency in Hz

1ȍ

2ȍ

3ȍ

4ȍ

5ȍ

6ȍ

7ȍ

8ȍ

9ȍ

0.1 0.2 0.3 0.4

in Hz

Fig. 8-19 Campbell diagram with natural frequencies of the tower-nacelle system and the cou-

pled blade – drive train system of a typical 1.5 MW wind turbine with variable rotational speed

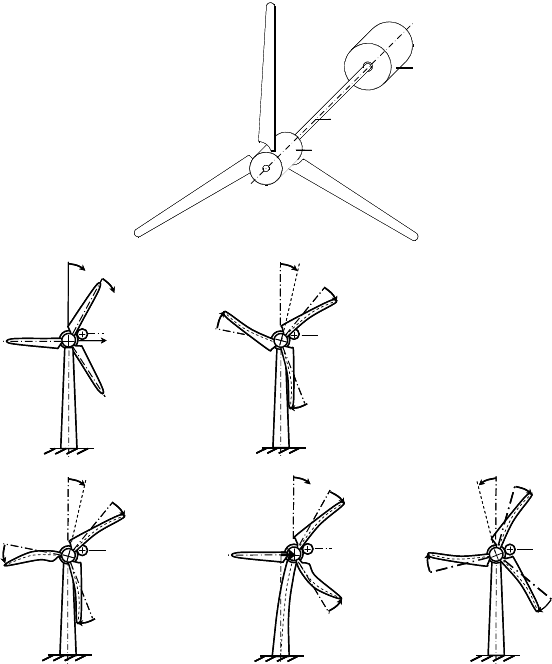
Fig. 8-20 top shows a simplified drive train model, where the blades are elastic. In

eigenmode I the blades and the hub oscillate together against the generator. In

eigenmode II, which is sometimes called lambda-eigenmode due to its

-shape, two

blades bend together in the edgewise direction and the third blade balances them

with doubled amplitude. Eigenmode III is characterised by two blades vibrating

against each other while the third stays calm (Y or tuning fork eigenmode).

Eigenmodes II and III are not coupled with the drive train torsion. The bending

moments at the hub are balanced. The corresponding natural frequencies are

(nearly) similar to the natural frequencies obtained for a rigid clamping of the

blade. However, with eigenmode III the tower shows a small accompanying

motion. In eigenmode IV the blades retain the packet-shaped vibration of Eigen-

mode I, but now the body of the hub vibrates in opposition to the blades. Since in

the model we allowed five degrees of freedom (for each blade an individual

edgewise degree of freedom, plus one for the hub-gearbox unit and one degree of

freedom for the generator) there is one natural frequency and eigenmode missing:

it is the “rigid-body degree of freedom”, the free unbound rotation of the entire

drive train which has the natural frequency of zero.

8.2 Free and forced vibrations of wind turbines - examples and phenomenology

296

Rotor (mit Getriebe)

Torsionsfeder

Generator

Torsion spring

Rotor (and gear box)

Rotor (mit Getriebe)

Torsionsfeder

Generator

Torsion spring

Rotor (and gear box)

Hub

-2

-1

Nacelle

Mode II

Mode III

Mode IV

Mode I

Hub

-2

-1

Nacelle

Mode II

Mode III

Mode IV

Mode I

Fig. 8-20 Eigenmodes of coupled blade-drive train system, eigenmodes I, II and IV coupled

with the drive train torsion, mode III coupled with the lateral nacelle vibration

1ȍ-Shift

Another typical effect in the overall system is the 1ȍ-shift. Mass unbalances as

well as an aerodynamic unbalance (blade angle or twist angle deviations) excite

vibration of the tower head with the frequency 1ȍ equal to the rotational fre-

quency in the lateral direction of the nacelle, see section 8.2.1.

These lateral vibrations of the nacelle act in the rotating system as a 2ȍ base

excitation (with twice the rotational speed) of the rotor blades in the edgewise di-

rection [11]. If the first two natural frequencies of the blades are close to double

or triple the maximum rotor speed, resonance problems may be provoked. This

1ȍ-shift is familiar to us already from gravitational influences: considered in the

8 Structural dynamics

297

inertial system without rotation, 0ȍ, the gravity force acts constantly on the

blades, whereas in the rotating system it acts periodically with the rotational fre-

quency 1ȍ. Therefore, in the resonance diagram of a three-bladed wind turbine,

Fig. 8-19, not only are the beams of the 1ȍ-, 3ȍ-, 6ȍ-, etc. excitations shown but

also the one for the 2ȍ excitation.

Simulation of the overall system dynamics

For larger wind turbines in the early design stages a model for the overall system

dynamics is developed, which considers all the couplings between the sub-

systems. It also comprises the electrical and electro-mechanical (or hydraulic)

degrees of freedom of the control and controllers. The solution of these “equations

of motion” is then calculated in the time domain by digital simulation. Compared

to the consideration in the frequency domain this has the advantage that even non-

linearities and transient processes may easily be considered. Section 8.3 gives an

introduction to the common procedures.

8.2 .5 Instabilities and further aeroelastic problems

Aeroelastic instabilities

In the discussion of the shut-down of a wind turbine we saw how slowly the

natural vibrations of the tower-nacelle system decay, Fig. 8-11, since in this case

there are only small damping forces from the flange connections of the tower and

from the soil.

However, if the machine operates close to the design tip speed ratio, the nacelle

vibrations in the axial direction and the blade vibrations in the flapwise direction

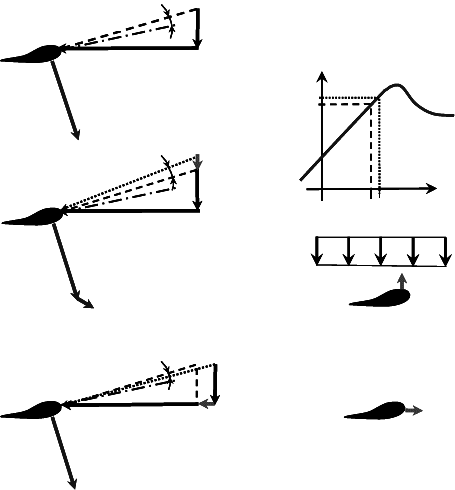
are well damped by aerodynamic forces. Fig. 8-21 shows in the middle how a

(flapwise) movement of the blade against the wind direction changes the triangle

of velocity. An additional lift ǻdL is produced which acts against this movement,

i.e. damps it. However, it also becomes clear that if the wind turbine operates in

the region of separated flow (i.e. stall) which is found to the right of the maximum

of the lift curve c

(

) then the deviation c

´ of the lift coefficient changes its

sign. The additional lift ǻdL produced by the flapwise movement becomes nega-

tive which means that vibrations are “fuelled” by the reduced damping. If there is

insufficient “structural damping” then the natural vibrations increase and instabil-

ity occurs. Of course, in the stall region the drag forces from c

have to be con-

sidered as well, so this case again becomes a little more complicated [12, 13].

8.2 Free and forced vibrations of wind turbines - examples and phenomenology

298

The edgewise movements of the blade provide only very small aerodynamic

damping, which may be concluded from Fig. 8-21 (bottom). Since the circumfer-

ential speed u is much bigger than the wind speed v

in the plane of rotation, the

aerodynamic forces – and above all the angle of attack

- merely change if

edgewise movements occur. The additional edgewise velocity 'u

edge

is small

compared to the circumferential speed u, consequently vibration modes where the

edgewise movement dominates are merely damped and therefore imply the danger

of instability. Therefore, there are sometimes dampers for the edgewise move-

ments installed in the blade tips of stall-controlled wind turbines (e.g. LM blades).

ǻv

Flap

ǻu

Edge

ǻdA < 0

< 0

ǻu

Edge

ǻv

Flap

ǻdA > 0

ǻv

Flap

ǻu

Edge

ǻdA < 0

< 0

ǻu

Edge

ǻv

Flap

ǻdA > 0

'dL > 0

'dL < 0

ǻv

Flap

ǻu

Edge

ǻdA < 0

< 0

ǻu

Edge

ǻv

Flap

ǻdA > 0

ǻv

Flap

ǻu

Edge

ǻdA < 0

< 0

ǻu

Edge

ǻv

Flap

ǻdA > 0

'dL > 0

'dL < 0

Fig. 8-21 Effect of flapwise bending and edgewise bending on the aerodynamic forces, aero-

dynamic damping and negative damping. Reference location (top), flapwise movement (middle),

edgewise movement (bottom)

8 Structural dynamics

299

Further aeroelastic problems

There are further aeroelastic problems which may occur, e.g.

- Stall-induced edgewise vibrations, provoked by flow separation which

may be reduced by dampers close to the blade tip (see above and cf.

chapter 3) [14]

- Unstable torsional drive train vibrations with the strong involvement of

edgewise blade movement and generator (or generator-converter system)

- Vibrations of the blade pitch controller, where the axial vibrations of the

tower-nacelle system (u,



) suggest incorrect wind speeds v

± u



, instead

of the real wind v

. The consequent action of the controller reduces the

aerodynamic damping or even actively amplifies the tower-nacelle vibra-

tions (see chapter 12)

- The nacelle whirl [11, 14] where the hub centre of the rotor propagates on

an elliptic orbit around its rest position

- Unstable lateral tower-nacelle vibrations [13]

- The fluttering known from aviation and the aerodynamics of buildings

where combined torsional and flapwise vibrations of the blade have an

unfavourable influence on the aerodynamic forces so that vibrations may

become unstable.

8.3 Simulation of the overall system dynamics

Since the wind and operating conditions of wind turbines are non periodic or tran-

sient, an analytical model may only rarely be applied in a way that makes it possi-

ble to determine deformations and stresses directly. Instead, the analysis of the

wind turbine behaviour as well as the design of the force-transmitting components

or the yield estimation is commonly based on simulations in the time domain

[1, 15].

Simply speaking the mechatronic model of the wind turbine is exposed for a

manageable time period to a “numerical wind” which is as close to reality as pos-

sible. This procedure is enhanced for offshore wind turbines by the simulation of

the swell, and in special cases also by the determination of loads during earth

quakes. The simulation calculations are used in essence to obtain the following

information:

- Internal forces and moments in certain relevant turbine components as

input for the component design procedure and for certification

- Determination of the wind turbine behaviour under all occurring operating

conditions for design validation and determination of the power curve

- Design and optimization of the control system

8.3 Simulation of the overall system dynamics

300

8.3.1 Modelling in simulation programs

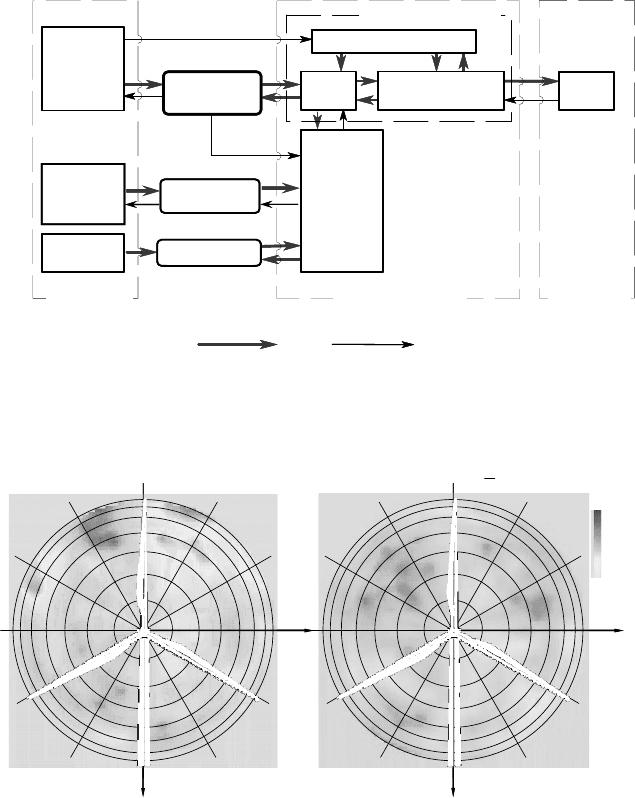
In general, the applied simulation models are divided into three sub-models, Fig.

8-22:

- Time series model of the environmental conditions (wind field, swell, etc.)

as input

- Model of the aerodynamics at the rotor blades

- Model of the structural dynamics of the wind turbine (including electrical

system and control behaviour)

The basic consideration in selecting the applied models is

Depth of modelling versus speed of simulation.

Therefore, different kinds of models are applied in parallel, of course depending

on the requirements which have to be satisfied. Pre-design studies serving for a

first estimation of the power performance and the wind turbine stress may be cal-

culated with models of low complexity which require less computing time.

Extended analysis of the controller behaviour requires partly a very complex wind

turbine model and consumes correspondingly more computing time. A complete

calculation for certification comprises the analysis of up to several hundred simu-

lation runs which have to be performed several times in the iteration loops of the

design process. Therefore, the applied models are just detailed enough for a suffi-

cient determination of the internal forces and moments required for certification –

a closer consideration of the components is then not possible.

Modelling of the wind field

One of the challenges of the wind turbine simulation is modelling the (unsteady)

wind as simulation input. This wind is basically one main reason for the necessity

of the simulations. Not long ago, it was thought that in the course of the design

calculations it would be sufficient to apply simple wind models consisting of a

steady inflow, deterministic gusts and superimposed vertical wind profile or

oblique flow. Many loads could then be determined with models according to the

ones discussed in the sections 8.1 and 8.2. But the growing influence of the fatigue

analysis in the course of the design led to a stronger emphasis on the turbulent

fraction of the wind.

8 Structural dynamics

301

Dynamic Influence:

Aerodynamic

Loads

Wind Field

Soil

Soil Dynamics

Grid

Support

Structure

(Tower &

Foundation)

Electro-Mechanical

Conversion System

Controller

Rotor

Wind Energy Converter ConsumptionEnvironment

Wind Turbine

major

minor

Aerodyna-

mic loads

Rotor

Controller

Electro-mechanical

conversion

Rotor-nacelle-unit

Grid

Wind turbine ConsumerEnvironment

Soil

Soil dynamics

Support

structure

(tower and

foundation )

Dynamic influence:

big

small

Wind

field

Waves,

currents,

ice

Hydrodyna-

mic loads

Dynamic Influence:

Aerodynamic

Loads

Wind Field

Soil

Soil Dynamics

Grid

Support

Structure

(Tower &

Foundation)

Electro-Mechanical

Conversion System

Controller

Rotor

Wind Energy Converter ConsumptionEnvironment

Wind Turbine

major

minor

Aerodyna-

mic loads

Rotor

Controller

Electro-mechanical

conversion

Rotor-nacelle-unit

Grid

Wind turbine ConsumerEnvironment

Soil

Soil dynamics

Support

structure

(tower and

foundation )

Dynamic influence:

big

small

Wind

field

Waves,

currents,

ice

Hydrodyna-

mic loads

Fig. 8-22 Block diagram of a simulation program with wind field model, rotor aerodynamics,

structural dynamics, influence of the generator and control system

5.85

v‘ in m/s

-5.75

t = t

v = 12 m/s

5.85

v‘ in m/s

-5.75

t = t

v = 12 m/s

Fig. 8-23 Simulated wind field in the rotor plane of a wind turbine at two consecutive times;

mean wind speed of 12m/s is subtracted

For this purpose, times series of the wind are generated which are based on the

statistical information of the wind under consideration, in general the mean wind

speed, the turbulence intensity, the length scale parameters and the turbulence

spectra (cf. section 4.2.5). These time series, which also incorporate wind compo-

nents perpendicular to the main wind direction, are applied to the swept rotor area

at up to several hundred points, Fig. 8-23. An important challenge in this context