Gasch R., Twele J. (Eds.) Wind Power Plants: Fundamentals, Design, Construction and Operation
Подождите немного. Документ загружается.

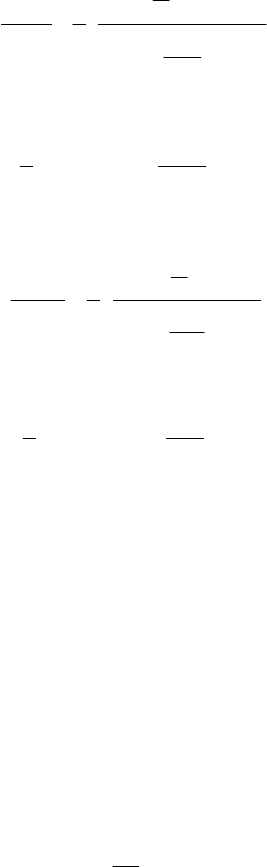
7.3 Tensile stress in the blade root resulting from centrifugal forces
262
6
2
1
2
2
1S
2
T
ax
S
,
hb
vlRc
zZ
lT
ax
axB
S
U
O
V
=
2
S
2
2
1T
3
hb
lR
vc
z
¸
¹
·
¨
©
§
SUO
(7.4)
6
2
1
2
2
1
3
M
,
,
bh
vRc
zZ
M
circ
brB
circB
S
U
O
V
=
2
3
2
1M
3
bh
R
vc
z
¸
¹
·
¨
©
§
SUO
(7.5)
Now, if all lengths (R, b, h, l
s
) are enlarged or reduced by the same factor, in
accordance with the law of similarity, the bending stress remains constant!
V
B
~ R
0
(7.6)
7.3 Tensile stress in the blade root resulting from centrifugal
forces
The tensile stress in the blade root due to the centrifugal force F
c
, can be obtained
by the cross sectional area A of the blade root:
A
F
c
Fc
V
(7.7)
Fig. 7-3 shows the change in centrifugal forces for a blade extension according to
the rules of similarity.
For a given distance l between rotor axis and the blade’s centre of gravity, the
centrifugal forces are:
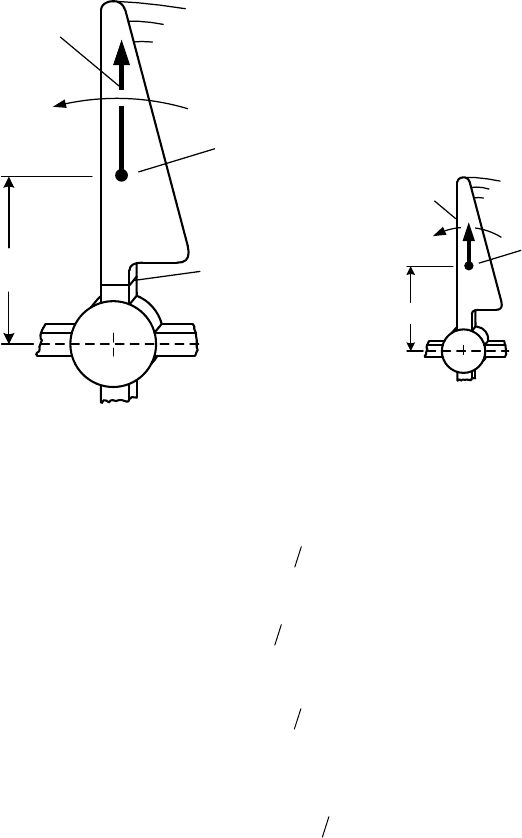
7 Scaling wind turbines and rules of similarity
263
F
c1
=
2
111
ȍlm (7.8)
F
c2
=
2
222
ȍlm (7.9)
2
F
R
U
2
:
2
m
2
l
2
A
R
U
1
F
1
m
1
:
1
l
Fig. 7-3 Centrifugal forces at the blade root when changing the rotor diameter
Applying the rules of similarity yields:
3
1212
RRmm , (7.10)
1212
RRll
and (7.11)
2
21
2
1
2
2
RRȍȍ . (7.12)
We thus obtain:
2
12
2
1112
RRȍlmF
c
(7.13)
7.4 Bending stresses in the blade root due to weight
264
The cross sectional area of the blade root is:
2
1212
RRAA (7.14)
If this term is inserted into equation (7.7), we obtain the following equation for the
tensile stress in the blade root of the enlarged blade:
1
1
1
2
121
2
12
2
111
2
2
2 Fc
cc
Fc
A
F
RRA
RRȍlm
A
F
VV
(7.15)
The tensile stress in the blade root due to centrifugal forces is then independent of
a change in the rotor diameter!
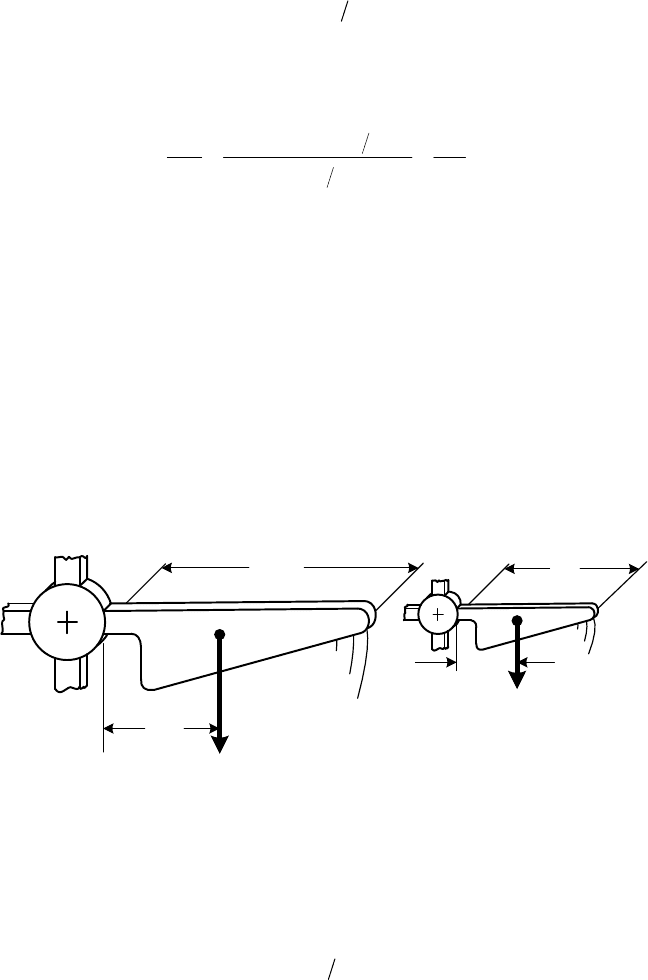
7.4 Bending stresses in the blade root due to weight
The bending moment M
B,W
in the blade root due to the blade weight mg acting at
the distance
l between the blade root and blade’s centre of gravity is:
M
B,W
= m g· l . (7.16)
2
R
2
l
2
m
g
1
R
1
l
1
mg
Fig. 7-4 Bending moment at the blade root due to weight influence when changing the rotor
diameter
Fig. 7-4 illustrates the impact of weight when comparing two blades of different
length. From the rules of similarity we obtain again for the scaling factor (R
2
/R
1
):
m
2
=
3
121
RRm and (7.17)
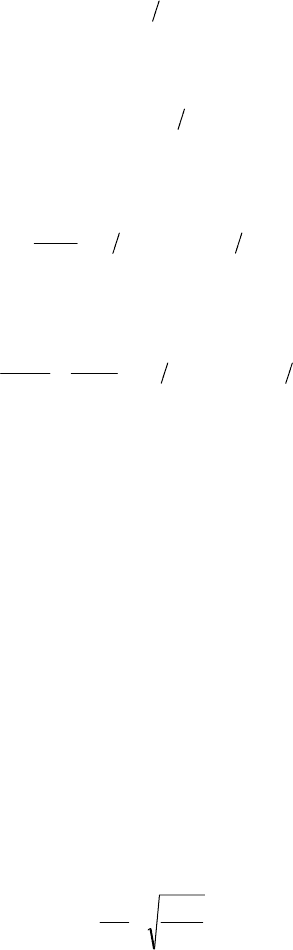
7 Scaling wind turbines and rules of similarity
265
l
2
=
121
RRl . (7.18)
This gives
4
121,B2,B
RRMM . (7.19)
The section modulus Z for a rectangular blade root, according to Fig. 7-2, is:
3
121
3
12
2
11
2
6
RRZRR
bh
Z (7.20)
Thus, the ratio of the bending stresses due to the weight is:
121,12
1
1,B
2
2,B
2,
RRRR
Z
M
Z
M
BB
VV
(7.21)
This means that the bending stress in the blade root due to the weight rises linearly
with the increase in the rotor diameter. This explains why the wind turbines cannot
be enlarged ad infinitum. It also limits the application of the rules of similarity for
extremely large turbines, where weight is the limiting factor for the turbine size.
Light weight design then becomes extremely important.
7.5 Change in the natural frequencies of the blade and in the
frequency ratios
To illustrate how the natural frequencies of the blades change if they are enlarged
or reduced in accordance with the rules of similarity, we assume (for the sake of
simplicity) an untwisted, homogeneous rectangular blade with a rigid attachment
to the hub (Fig. 7-5).
According to [4] the natural frequencies of this vibrating beam are as follows,
if we ignore the centrifugal stiffening and take the eigenvalues
/
n
from table 7.2:
Z
n
=
P
ǿǼ
R
ȁ
2
2
n
(7.22)

7.5 Change in the natural frequencies of the blade and in the frequency ratios
266
Table 7.2 Eigenvalues
/
n
of the fixed end beam (cantilever)
n 1 2 3 ....... n (large values)
//
n
1.8571 4.6941 7.8531 .......
212
S
|
n
For the natural frequencies in direction of the flap deflection (low stiffness), we
obtain the n
th
natural frequency Z
n
, using the mass per (blade) length
P
=
U
b h (7.23)
and the geometrical moment of inertia,
12
3
hb
I , thus (7.24)
UU
Z
1212
2
2
n
3
2
2
n
Ǽ
R
hȁ
hb
hbǼ
R
ȁ
n
. (7.25)
For a change in rotor diameter, this results in:
1,n
2,n
Z
Z
=
2
21
2
12
Rh
Rh
=
2
1
R
R
(7.26)
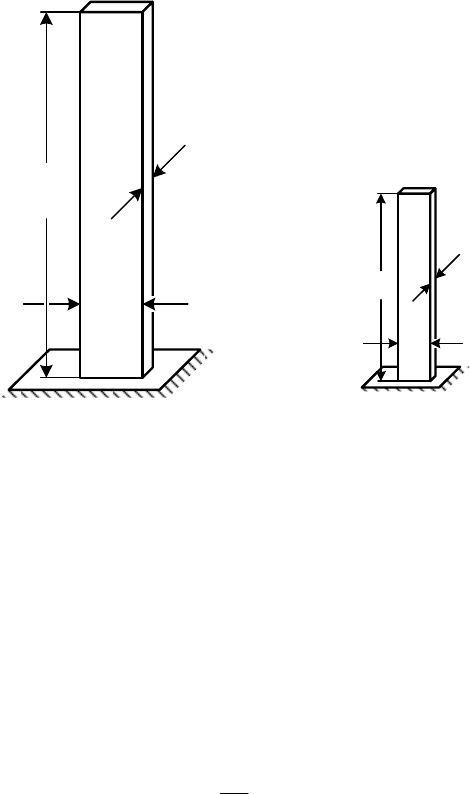
7 Scaling wind turbines and rules of similarity
267
2
R
2
h
2
b
1
R
1
h
1
b
Fig. 7-5 Untwisted, homogeneous rectangular blade; influence of the change of the rotor dia-
meter on the flapwise natural frequency
The natural frequencies in direction of edgewise vibration are obtained in the same
way using the geometric moment of inertia for the stiff direction, i.e. b and h are
interchanged. It follows that the natural frequencies change in inverse proportion
to the change in rotor diameter. This law for the natural frequencies holds true
even for tapered and twisted blades.
The excitation frequencies of the blade due to the tower shadow effect, mass
unbalance, aerodynamic unbalance or the height-related wind profile are all pro-
portional to the rotational speed :. But as :, like the natural frequencies, is in
inverse proportion to the change in rotor diameter, the frequency ratio K
n
between
excitation frequencies and natural frequencies remains constant whether the rotor
is scaled up or down!
K
n
=
n
Z
ȍ
~ R
0
(7.27)
7.6 Aerodynamic damping
Since the structural damping at a wind turbine is small, the damping of vibrations
comes, on the one hand, from the generator, which can only be manipulated in the
rotational degree of freedom, and on the other, from the aerodynamic forces at the

7.6 Aerodynamic damping
268
rotor - though, unfortunately, they may sometimes even excite the vibrations [2,
6].
The rules of similarity also hold valid for the aerodynamic damping: The
damping ratio
D (dimensionless Lehr’s damping ratio, see equations (7.30) and
(8.8.)) is heavily dependent on the tip speed ratio of the operation points (partial
load!) but independent of the rotor radius.
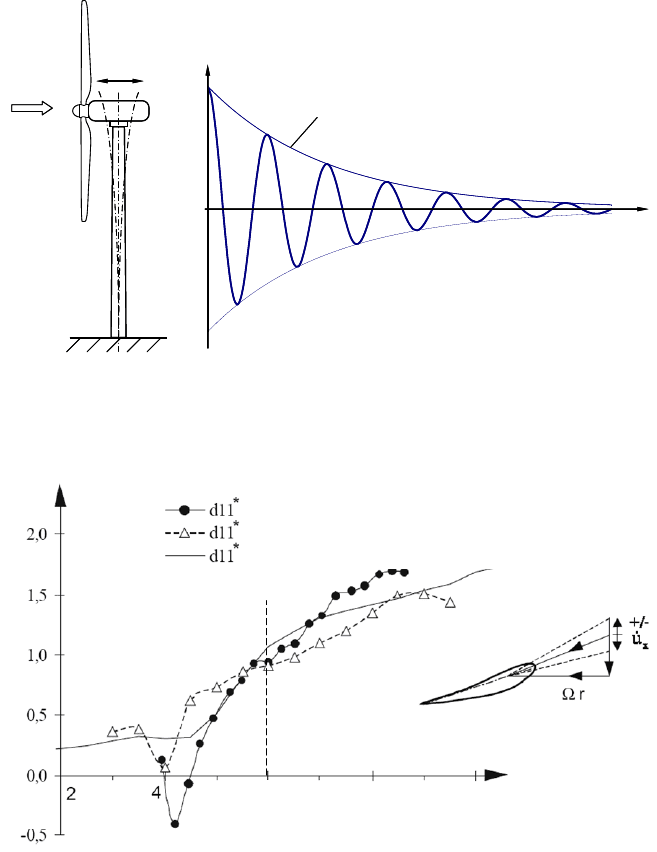
Fig. 7-6 shows, on the left, the tower-nacelle system vibrating in the axial
direction (i.e. the wind direction) and, on the right, for constant wind speed
v
Wind
, the
decaying curve of the damped vibration at natural frequency. A measured decay-
ing curve is displayed in Fig. 8-11. The aerodynamic damping coefficient
d
11
(
O
)
depends strongly on the tip speed ratio. The measured and calculated dimen-
sionless values
d
11
* are shown in Fig. 7-7 for a rotor dimensioned according to
Schmitz (
O
D
§ 6) where, [6],
d
11
(
O
) = d
11
*
2
R
v
Wind
2
ȡ
.
(7.28)
The damping force is obtained by multiplying of
d
11
with the vibration velocity u
which becomes obvious when comparing the dimensions.
The decay factor
G
, describing the envelope curve of the decaying natural
vibration, is given by [3, 4]
G
= d
11
/ (2 m) . (7.29)
The dimensionless damping ratio
D is obtained from the ratio of decay factor
G
and the natural frequency Z
0
(cf. chapter 8, dynamics) of the system without
damping
D(
O
) = d
11
(
O
)/ (2 m
Z
0
According to the rules of similarity the following relations are valid
mass
m ~ R
3
natural frequency
Z
~ 1/R and,
as explained above,
d
11
~ R
2
.
Therefore, the damping ratio
D of the axial tower-nacelle vibration is independent
of the radius of the wind turbine.
7 Scaling wind turbines and rules of similarity
269
Fig. 7-6 Axial deflection u(t) of the tower-nacelle vibration; fading out due to the decay factor G
of the damping
Ȝ
D
= 6
*
11
d
8
10 Ȝ
Measurement in free-stream channel
Measurement in closed channel
Theory
w
Ȝ
D
= 6
*
11
d
8
10 Ȝ
Measurement in free-stream channel
Measurement in closed channel
Theory
w
Fig. 7-7 Dimensionless damping coefficient d
*
11
(O) for a wind turbine in axial direction;
comparison of the theoretical curve and measurements in two different wind tunnels [from [2],
chapter 25, lit. 10]
There is a significant loss of damping when the flow separates, i.e.
O
< 5.
-1
0
1
0 2 4 6 8 10 12
v
Wind
u(t)
tporsuudum 0
11
t
e
G
t
u(t)
-1
0
1
0 2 4 6 8 10 12
v
Wind
u(t)
tporsuudum 0
11
t
e
G
t
u(t)

7.7 Limitations of up-scaling - how large can wind turbines be?
270
7.7 Limitations of up-scaling - how large can wind turbines be?
In the calculations for dimensioning and partial load operation of wind turbines,
chapters 5 and 6, it was always assumed that the lift and drag coefficients,
c
L
and
c
D
, are independent of the relative velocity w. This holds true for common airfoil
profiles as long as the Reynolds number
X
wc
viscositykinematic
velocityrelative ·length chord Profile
Re
is larger than 200,000. For
small wind turbines (D < 5 m) and in wind tunnel ex-
periments this requirement leads to some problems. For Reynolds numbers below
Re < 50,000, even thin and sharp low-Reynolds profiles [5, 7] no longer produce
any lift. This limits
down sizing.
In section 7.4 it was shown that the bending stress due to blade weight in-
creases proportionally to the blade radius when scaling up according to the rules
of similarity - and thus creates an
upper limit for wind turbine construction. This
limit is higher
- the higher the fatigue strength against alternating bending,
V
BW
, and
- the smaller the density
U
of the material used.
That is the reason why glass-fibre reinforced plastics (GFRP) replaced alumin-
ium, and why carbon-fibre reinforced plastics (CFRP), which are even lighter and
stronger, are now being used more and more.
Light-weight design with all the weight-saving tricks used in construction plays
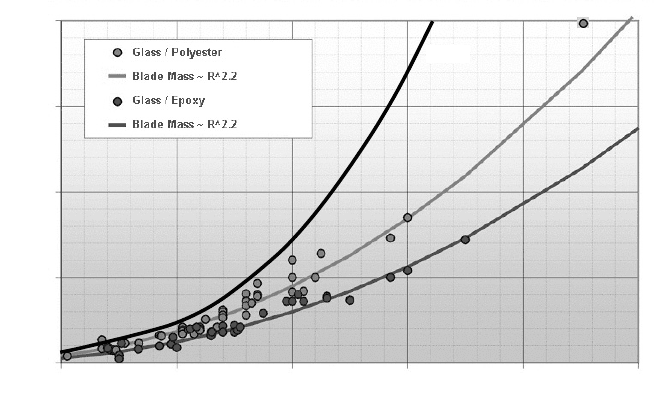
an important role. Fig. 7-8 shows the blade weight versus the rotor radius, or rotor
diameter, for some wind turbines. If the blade mass is scaled up purely using the
rules of similarity with the starting point
m = 300 kg at D = 21 m, we obtain the
curve (m ~
R
3
) proportional to the cube of the radius. However, design engineers
have achieved a reduction in the rotor blade mass by means of light weight design:
For both material combinations glass/polyester and glass/epoxy the fitted curves
for the blade mass are proportional to (
R
2.2
).
Moreover, practical reasons prevent the rigid application of the scaling rules.
Wind turbines situated inland need high towers (
H/D > 1) to escape the boundary
layer close to the ground. Wind turbines at the coast need only smaller towers
(
H/D < 1). For small wind turbines or battery chargers, the ratio is often H/D > 2.
The laws of similarity allow quickly to find the shape of a future design. And
they reveal where problems are to be expected.
7 Scaling wind turbines and rules of similarity
271
Rotor diameter D in m
Blade mass m in t
Euros / Germany
m ~ R
3
20
15
10
5
0
20 40 60 80 100 120
Rotor diameter D in m
Blade mass m in t
Euros / Germany
m ~ R
3
20
15
10
5
0
20 40 60 80 100 120
Fig. 7-8 Increase of the blade mass with the diameter; real mass (interpolation m ~ R
2.2
) and
theoretical curve (m ~ R³)
References
[1] Wiedemann, J.: Leichtbau (Light weight construction), Band II, Kapitel 4, Springer
Verlag, Berlin 1989
[2] Nordmann, R, Gasch, R., Pfützner, H.: Rotordynamik (Rotor dynamics) (2
nd
edition),
Springer Verlag Berlin, 2002
[3] Magnus, K., Popp, A.: Schwingungen (5. Auflage) (Vibrations, 5th edition), Teubner
Verlag, Stuttgart, 1997
[4] Gasch, R., Knothe, K.: Strukturdynamik I und II (Structural dynamics I and II),
Springer Verlag Berlin, 1987/89
[5] Althaus, D.: Profilpolaren für den Modellflug (Profile polar characteristics for
aeromodelling), Neckar-Verlag, VS-Villingen, 1980
[6] Kaiser, K.: Luftkraftverursachte Steifigkeits- und Dämpfungsmatrizen in Windturbinen
(Aerodynamic damping and stiffness matrices of wind turbines), VDI-Fortschritt-
Bericht, Reihe 11 (VDI progress report, series 11) , Nr. 294, Düsseldorf 2000
[7] Althaus, D.: Niedriggeschwindigkeitsprofile(Low-Reynolds airfoil profiles), Vieweg
Verlag, Wiesbaden 1996
