Gasch R., Twele J. (Eds.) Wind Power Plants: Fundamentals, Design, Construction and Operation
Подождите немного. Документ загружается.

6.8 Extending the calculation method
232
section was determined. These two forces can be equated, when the following as-
sumptions hold true:
- The forces at the blade section cause a steady and homogeneous change in
the velocity of the air mass that flows through the ring section with the
area dA = 2
r dr.
- The air mass is only affected by the aerodynamic forces in the plane of
rotation. The stream filaments do not excert any forces on each other.
- The profile drag is very small and can thus be neglected.
These assumptions are approximately valid as long as the rotor runs near the de-
sign tip speed ratio. During start-up (
<<
D
) of a turbine with a high tip speed
ratio, air flows through the rotor without being influenced by the blades. However,
during load-free idling (
>
D
), the deceleration of the air is so heavy (v
2
< v
1
/2)
that some of the retarded air mass flows rather around the outside of the rotor than
through the rotor area. This loss of utilized air mass is not considered in the for-
mula of linear momentum we used in section 6.1. Furthermore, the profile drag is
negligible only for operation with the design tip speed ratio. We already men-
tioned these effects when discussing the dimensionless characteristic curves in
sections 6.3 and 6.4 and considered them in the turbine performance characteristics
of sections 6.5 and 6.7. In the following, better late than never, the calculations of
section 6.1 will now be extended to include these influences in the iteration
algorithm.
6.8.1 Start-up range of
<
D
(high lift coefficients)
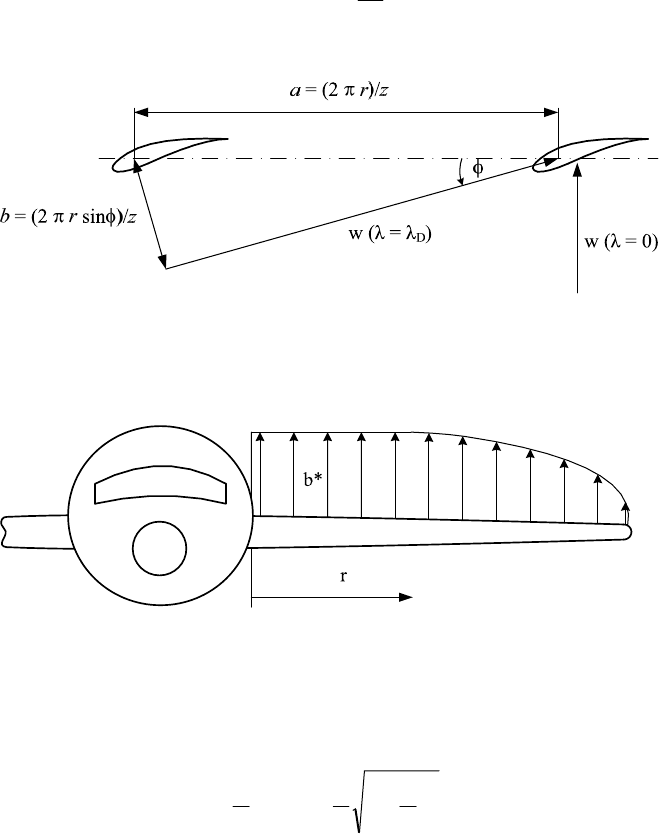
A turbine with a high tip speed ratio has few and slender blades. These apply a
force to the air masses that flow through the ring section with the area 2
r dr, cf.
Fig. 5-14. An individual airfoil can affect the air mass in its vicinity only in a cer-
tain effective width b*.
If the rotor runs at the design point of
D
, the relative velocity w has the angle
with respect to the rotor plane, Fig. 6-19. The width b of the region the blade
should affect is comparatively small, b = (2
r sin
/z, because, due to the small
angle of attack, the incident relative velocity is nearly parallel to the profile chord.
In contrast, at standstill the individual blade should affect a width of a = 2
r/z
(i.e. the circumferential distance between the blades) which is usually significantly
larger than its actual width of influence b*. Therefore, during standstill (and start-
up) of a turbine with a high tip speed ratio, some of the air flows through the plane
of rotation without being disturbed and utilized by the blades.
How large is the effective width b* of the region where a blade affects the air
masses? Strictly speaking, its influence reaches into infinity - it only decreases
rapidly with growing distance. From the Prandtl airfoil theory [4], we obtain the
maximum of air mass for which a blade can cause a constant change in speed.
6 Calculation of performance characteristics and partial load behaviour
233
From that, we can estimate the effective width b*. For the airfoil of an airplane,
Prandtl proved that for an elliptic lift distribution (Fig. 6-20), the air flow at each
blade section is directed downwards at an identical angle.
Far downstream of the airfoil, the air moves downwards with a speed of 2
v
which depends on the lift coefficient c
L
, the blade chord c and the relative velocity
w.
R
c
cwv
L
22 (6.11)
Fig. 6-19 Width of area in which the rotor blades should influence the flow: width a at standstill
(
= 0) and b at the design point (
=
D
)
Fig. 6-20 Area in which an airfoil affects the air flow with reduced influence close to the tip
If a similar elliptic lift distribution is assumed for the rotor blade, the lift of each
blade section can be calculated by
2
L
2
1
4
2
R
r
cdrcwdL
. (6.12a)

6.8 Extending the calculation method
234
The mass flow is now the product of air density
, relative velocity w and the still
unknown area b* dr around the blade where it affects the flow. The lift obtained
from the principle of linear momentum with a change in speed of 2
v, equation
(6.11), is therefore
vmddL
2
R
c
cwdrbwdL
L
2* (6.12b)
Equating the lift in (6.12a) to that in (6.12b) gives us the maximum area b* dr
perpendicular to w that can be affected and this in turn gives us b*
drRrRdrb
2
)(1* . (6.13)
The maximum effective width b* is independent of the blade chord c and the lift
coefficient c
L
! According to this equation, a blade cannot deflect any air mass at
all at the blade tip (r = R).
If in Fig. 6-19 we take b = b* and use the width a between the blades, we
obtain the maximum relative velocity angle
max
up to which the air mass in the
ring section of 2
r dr is affected and utilized. The maximum relative velocity
angle
is then dependent on the number of blades z
)(2
)(1
sin
2
max
Rr
Rrz
(6.14)
If, for the range of
<
A
, in the course of the iterative calculation, we obtain
larger values
max
of the relative velocity angle, we have to replace sin
by
sin
max
in the iteration equation. This makes allowance for the fact that then a
fraction of air mass flows through the swept rotor area without being utilized.
6.8.2 Idling range of
>
D
(Glauert’s empirical formula)
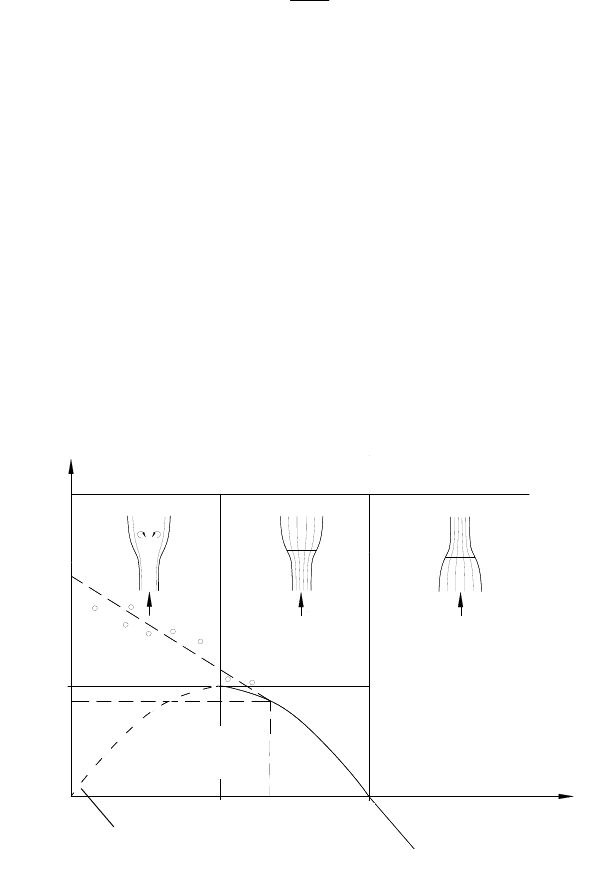
If the rotor is idling load-free the thrust coefficient of a turbine with a high tip
speed ratio, cf. Fig. 6-4, approaches the drag coefficient of a solid circular disk, cf.
Fig. 2-19.
6 Calculation of performance characteristics and partial load behaviour
235
If therefore the wind speed v
2
in the plane of rotation is slowed to zero, the relative
velocity angle and consequently the mass flow approaches zero, too. Using the
principle of linear momentum, we would then obtain the thrust force
0sin
2
vdr
z
r
wvmddT
(6.15)
i.e. the thrust becomes zero, which does not seem altogether logical. Formally, it is
correct that if no air flows through the plane of rotation, we do not need any force
to retard it. However, in reality, the point is that the retarded air no longer flows
through the rotor plane as assumed in the formula of linear momentum, but passes
outside around the circular rotor swept area as it does with a solid circular disk.
This kind of flow is not taken into account in the stream tube theory that has been
applied so far.
In order to consider this fluid dynamic effect in the calculation of rotor charac-
teristics we will now apply an approximated approach, without which it would be
necessary to compute the entire three-dimensional flow in the area from -∞ to +∞.
The thrust forces of this operating state were measured and investigated by
Glauert (1926) and Naumann (1940), [2, 3]. The purpose of the measurements was
to determine how efficiently a propeller airplane could be slowed down if the pro-
peller blades were pitched so that they act contrary to the direction of flight. Glauert
discovered that the thrust force can be calculated using our formula of linear
momentum until approximately v
2
≥ 2/3 v
1
.
Betz-Auslegung
Physically not
reasonable
Principle of the linear
momentum with disk
area
1/2 2/3 1
v
2
/v
1
1
8/9
Glauert
(empirical)
Thrust coefficient
v
2
v
1
v
1
turbulent
attached flow
Turbine range
Propeller range
c
T
Betz dimensioning
2
Betz-Auslegung
Physically not
reasonable
Principle of the linear
momentum with disk
area
1/2 2/3 1
v
2
/v
1
1
8/9
Glauert
(empirical)
Thrust coefficient
v
2
v
1
v
1
turbulent
attached flow
Turbine range
Propeller range
c
T
Betz dimensioning
2
Fig. 6-21 Thrust coefficient according to the principle of linear momentum and according to
Glauert’s empirical approach in the range of 0 < v
2
/v
1
< 0.5, [2,3]
6.8 Extending the calculation method
236
For smaller v
2
, i.e. larger
, the thrust force, and correspondingly the thrust coeffi-
cient, increases steadily and reaches a value of twice the dynamic pressure at
v
2
= 0 m/s (i.e.
= 0°), see Fig. 6-21. Given this finding, the air mass that is
retarded by the forces of the blade can be approximated depending on the relative
velocity angle using a continuous function, for which the following conditions
apply:
- For v
2
= 0, twice the dynamic pressure is obtained
- For v
2
= 2/3 v
1
, the value of the function and the slope must agree with the
Betz optimum dimensioning.
Using the substitution:
)32(sin
sin
1
y
the mass flow is described as follows:
42
1
929
3
2
sin
4
12
yywdr
z
r
md
(6.16)
This approximation is only valid for small relative velocity angles
1
of the undis-
turbed flow! The angle
1
has to be so small that the approximation sin
1
≈
1
is
valid. For turbines with a high tip speed ratio, this operational state is reached, for
instance, during load-free idling.
Equation (6.5) can still be used for the calculation of the relative velocity angle
,
however, for
≤ 2/3
1
(i.e.
>
D
) the term of the air mass (8
r/z sin
has to
be substituted by the larger air mass of equation (6.16) (i.e. sin
is replaced by the
expression in the large brackets).
6.8.3 The profile drag
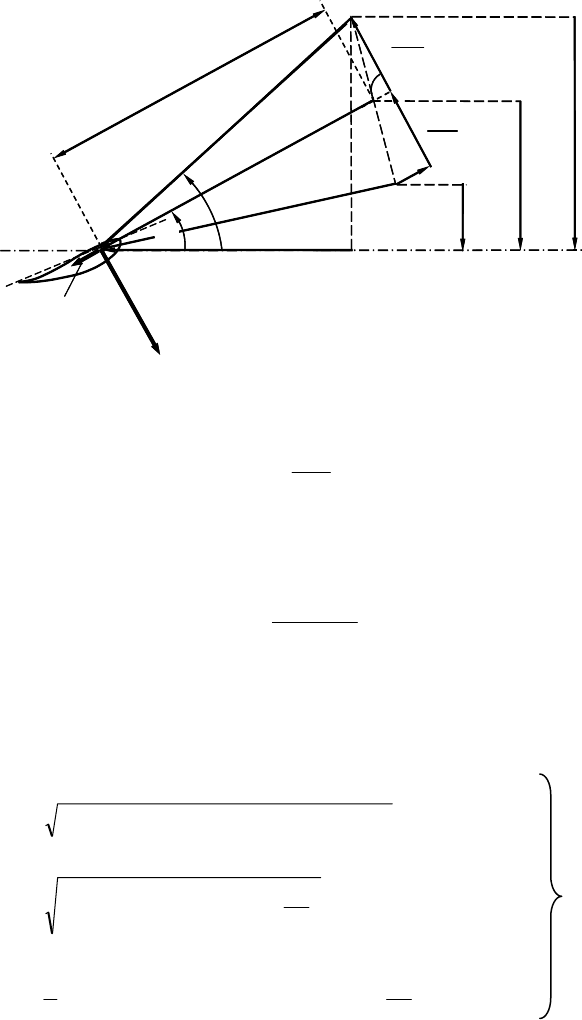
For an airfoil, the profile drag acts in parallel to the relative velocity. The profile
drag reduces the relative velocity w by the velocity difference
w which denotes
the component parallel to the profile drag of the change of relative velocity, Fig.
6-22. For the sake of clarity, the component of the velocity change parallel to the
lift is denoted w. The velocity difference w is obtained again from the force
equations of the airfoil theory and the principle of linear momentum.
The calculation of the drag force at a blade section using the airfoil theory was
derived in equation (5.28) of chapter 5. The principle of linear momentum can
also be used to obtain the drag force at a blade section:
6 Calculation of performance characteristics and partial load behaviour
237
ϕ
u = Ω r
ϕ
1
v
1.ax
= v
1
v
2.ax
w
3
w
1
sinw
2
w
1
dL
.
dD
v
3.ax
w
2
w
w
2
=
w
=
w
1
c
o
s
(
ϕ
1
-
ϕ
)
–
w
/
2
(ϕ
1
-ϕ)
ϕ
u = Ω r
ϕ
1
v
1.ax
= v
1
v
2.ax
w
3
w
1
sinw
2
w
1
dL
.
dD
v
3.ax
w
2
w
w
2
=
w
=
w
1
c
o
s
(
ϕ
1
-
ϕ
)
–
w
/
2
(ϕ
1
-ϕ)
Fig. 6-22 Flow conditions at the blade section
wdr
z
r
wwmddD
sin
2
. (6.17)
By equating both forces, the velocity difference
w is obtained depending on the
relative velocity w at the blade section
sin4
AD
r
ccz
ww
. (6.18)
Observing the flow from the rotating blade as the reference (rotating frame of ref-
erence), the far downstream wind has the velocity w
3
. As w
3
is smaller than the
undisturbed upstream relative velocity w
1
, the rotating observer will note that the
power dP is extracted from the air:
2
)cos(
2
1
2
)cos(2
)cos()sin(
11
2
3
2
1
11
2
13
2
11
2
113
w
wwmdwwmddP
w
wwww
wwww
(6.19)

6.8 Extending the calculation method
238
This power dP can also be derived from the product of drag force dD and relative
velocity w. By equating these two power expressions and using w from equation
(6.18), the velocity w at the blade section is obtained:
2
)cos(
11
w
wwmdwwmdwdDdP
(6.20)
)(sin
8
sin
8
)cos(
AD
11
cc
z
r
z
r
ww
. (6.21)
Since the lift force dA is also calculated using the relative velocity w, taking into
account the profile drag changes the basic equation (6.5) of the iteration as
follows:
wmdcdrcwdL
)(
2
AL
2
0)tan()(sin
8
)(
1ADAL
cc
z
r
cc (6.22)
6.8.4 The extended iteration algorithm
Considering the flow of unused air around the swept rotor area (Prandtl), the
Glauert empirical formula for the flow near to the tip and the profile drag, the
iteration algorithm for every blade section is as follows:
1) Starting value:
1
,
2) Limiting angles of the relative velocity angle:
)(2
)(1
sin
2
max
Rr
Rrz
1min
3
2
sinsin

6 Calculation of performance characteristics and partial load behaviour
239
3) With this
:
r
A
→ c
L
(
A
) and c
D
(
A
) from the airfoil
profile characteristics
and substitution:
sin
x
Set
42
1
929
3
2
sin
4
1
yyx
with
)3/2sin(
sin
1
y
If
max
sin
x then modified according to Prandtl:
Set
max
sin
x
5) Solution of
1
tan
8
ADAL
crcx
z
r
crcf (6.22/ 6.23)
6) Verification:
If f > 0 then reduce and go back to step 3).
If f < 0 then increase and go back to step 3).
With this procedure we zero in on the relative velocity angle until the residual
reaches f = 0 m. Aerodynamics is once more reduced to searching the functions
zero.
To compute the iteration it is quite reasonable to select a suitable loop termina-
tion criterion for the residual f. Due to the profile chord length and the blade
radius in equation (6.23) f is dimensionful (meter); moreover for wind turbines
with a high tip speed ratio the chord length decreases strongly with increasing
radius. Therefore, it is not useful to apply one and the same termination crite-
rion (e.g. f < 0.002 m) for the entire blade: it is perhaps suitable for the small
blade tip, but unreasonable for the range of the maximum chord length of up to
4 m close to the blade root, where it is smaller than the manufacturing toler-
ances. In the course of programming the iteration this problem is solved by
transforming equation (6.22) into a dimensionless equation, e.g. dividing by the
chord length c. Then the percentage termination criterion for the residual f/c is
applicable along the entire blade radius.
7) The relative velocity w is calculated with the determined relative velocity
angle
and equation (6.21). Here the sin
should be replaced by the term x
from step 4) of the iteration algorithm.
8) The aerodynamic forces now obtained for the blade section are:
4) Verification:
If
min
sin
φ
<x , then modified according to Glauert:

6.9 Limits of the blade element theory and three-dimensional calculation methods
240
)()(
2
2
AL
cdrrcwdL
and )()(
2
2
AD
cdrrcwdD
and subsequently:
Thrust force: dT(r) = dL cos
+ dD sin
Circumferential force: dU(r) = dL sin
- dD cos
(6.24)
Torque moment: dM(r) = dU r
With the presented extended iteration algorithm of the blade element momentum
method it is possible to determine, with a fairly close approximation, the forces
and moments produced by the aerodynamics as well as the power of the wind tur-
bine rotor for the entire range of its performance characteristics.
6.9 Limits of the blade element theory and three-dimensional
calculation methods
The blade element method discussed in this chapter has the advantage of provid-
ing a comparatively accurate calculation of the performance characteristics with-
out requiring the solution of extensive systems of equations. However, it ignores
the fact that there are interactions between the flow in the different radial blade
sections. For the simplified approach, optimum rotor geometry and ideal lift dis-
tribution were assumed. In the range of low tip speed ratios (λ < λ
D
) and for non-
optimum rotor geometry, there may occur considerable discrepancies between the
calculated and the actual measured power. In particular, the beginning of the flow
separation (stall) cannot be predicted accurately. There are in the main three
effects which produce the divergence between calculation and actual values:
- Ignoring the real lift distribution
- Change of the lift curves by the 3-D effect
- Dynamic effects
In the following, various approaches for addressing these effects are discussed.
6.9.1 Lift distribution and three-dimensional effects
In the literature, there are different effects referred to as the "3-D effect":
- Induced velocities produced by the tip vortices,
- Modified profile characteristics due to the finite length of the blade,
- Modified profile characteristics due to Coriolis and centrifugal forces.
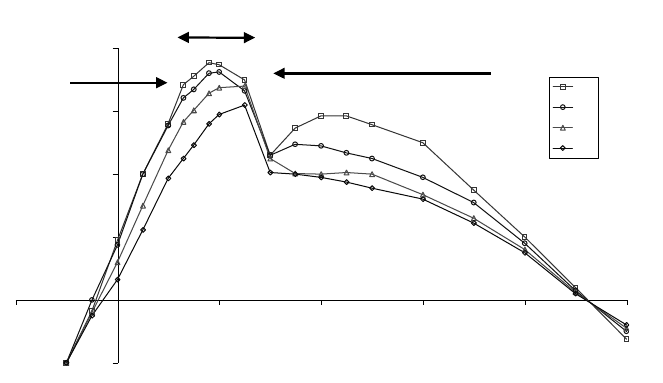
6 Calculation of performance characteristics and partial load behaviour
241
Fig. 6-23 Lift coefficient versus angle of attack for blades with different aspect ratio, [7, modi-
fied]
For attached flow the lift can be calculated with the Prandtl correction. Our
version, equation (6.22), assumes an elliptical lift distribution. More extensive cal-
culation procedures based on Panel methods (method of singularities) or Euler
equations are, however, only applicable for attached flow.
Generally the measured airfoil characteristics are available for the region with
attached flow up to the high lift region. Airplanes do not have separated flow
across the wing under normal flight conditions. Therefore, it is very difficult to get
accurate values from wind tunnel measurements for the region of separated flow.
So the database for post-stall values is very small. The last measured value for lift
and drag is usually for the angle of attack α
A.s
where the flow starts to separate.
The lift and drag values in the post-stall region with fully separated flow seem
to be quite similar for all airfoils. Here, it is possible to fall back on the aero-
dynamic characteristics of a flat plate where there are approximations for the region
of separated flow [8]. Based on this, Viterna and Corrigan formulated the descrip-
tion of the passage to the measurement data [e.g. in 26]. In the following we will
present their equations for the range of the angle of attack between 15 < α
A
< 90°.
For separated flow, the drag coefficient may be described as follows:
A2A
2
1D
cossin
BBc (6.25)
NACA 4418
-0.4
0
0.4
0.8
1.2
1.6
-20 0 20 40 60 80 100
inf.
12
9
6
attached flow
high lift region
Post Stall re
g
ion
A
s
p
ect ratio
A
c
L
[ ]
