Гаркушенко В.И. Лекции по ТАУ

Подождите немного. Документ загружается.

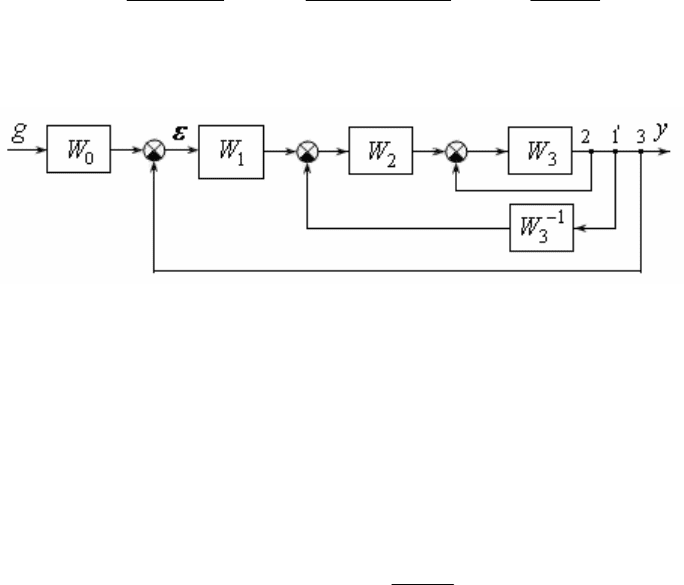
Для решения задачи необходимо привести структурную схему к виду

обобщенной структурной схемы рис. 5. Для этого узел 1 перенесем вперед че-

рез передаточную функцию

. Тогда получим структурную эквивалентную

схему рис. 12, для которой с помощью формул (1), (4) последовательно найдем:

0 1 2

1 2

W WW







2 3

2 3 3

W W

W W W















Рис. 12

Здесь в результате упрощения выражения полученной эквивалентной пе-

редаточной функции она приводится к виду

( ) ( )/ ( )

W p m p d p



. При этом вы-

ход системы имеет вид

( )

( ) ( ) ( ) ( )

( )

m p

Y p W p G p G p

d p

 



где,

0 1

( )

m m

m p b p b p b



   

  





0 1

( )

n n

d p a p a p a



   



  



Отсюда следует, уравнение в изображениях Лапласа

( ) ( ) ( ) ( )

d p Y p m p G p





которому с учетом обратного преобразования Лапласа соответствует диффе-

ренциальное уравнение

( ) ( 1)

0 1

( ) ( 1)

0 1

( ) ( ) ( )

( ) ( ) ( ).

n n

m m

a y t a y t a y t

b g t b g t b g t



   

   

  



  



(11)

Следует отметить, что из уравнения (11) при

( ) 0

g t



в общем случае не

следует уравнение свободных движений выхода

( )

y t

, зависящих от начальных

условий

(0)

(1)

(0)

y , …,

( 1)

(0)



, поскольку в полином

( )

d p



входит полином

знаменателя передаточной функции

( )

W p

Поэтому для анализа динамики свободных движений системы, вызван-

ных начальными условиями, при отсутствии входных сигналов необходимо оп-

ределить соответствующее дифференциальное уравнение. Для этого, например,

в уравнениях (6) следует положить



. Тогда получим уравнения

ос 2 1

W y y W W

 

  

из которых, для выхода

найдем





раз

1 0

W y

 

Полагая

раз

( ) ( )/ ( )

W p m p d p



, получим уравнение в изображениях Лапласа

( ) ( ) 0

D p Y p



, (12)

где

( ) ( ) ( )

D p d p m p

 

– характеристический полином замкнутой системы.

При этом свободное движение

( )

y t

определяется корнями характеристическо-

го уравнения

( ) 0

D p



. Действительно, уравнению (12) в изображении Лапласа

соответствует дифференциальное уравнение

( ) ( 1)

0 1

( ) ( ) ( ) 0

n n

a y t a y t a y t



   



. (13)

Тогда переходя к преобразованию Лапласа в уравнении (13) с учетом началь-

ных условий

(0)

(1)

(0)

y ,…,

( 1)

(0)



получим выражение

( ) ( )/ ( )

Y p M p D p



где

( )

M p

– полином, зависящий от начальных условий. Тем самым, независи-

мо от начальных условий оригинал

( ) { ( )}

y t L Y p



 определяется полиномом

( )

D p

или корнями уравнения

( ) 0

D p



В системе MATLAB предусмотрена возможность программно “набирать”

схему САУ путем предварительного ввода моделей простых звеньев и после-

дующего соединения этих звеньев в единую структуру.

Пример 3. Для структурной схемы рис. 11 при заданных передаточных

функциях можно найти передаточную функцию

для выхода

от входа

помощью следующих команд [2]:

Wa=append(W0,W1,W2,1,W3);

in=[1]; out=[5];

Q=[2 1 -5 0;3 2 -4 0;4 3 -5 0;5 4 0 0];

W=connect(Wa,Q,in,out)

2. Многомерные системы

Рассмотренные выше структурные схемы относятся к одномерным сис-

темам, поскольку имеют один выход. Если в системе имеется несколько выхо-

дов, то такая система называется многомерной или многосвязной, если выходы

в системе взаимосвязаны. Примером многомерной и многосвязной системы

может служить летательный аппарат, у которого управляемыми величинами

являются курс, углы тангажа и крена, скорость и высота полета.

В многомерных системах при нескольких входных воздействиях

( )

u t

i m

 изображение для выходной координаты

( )

y t

i l



определяется выра-

жением

( ) ( ) ( )

i ij j

Y p W p U p





, (14)

где

( ) ( )/ ( )

ij ij ij

W p m p d p



i l



;

j m

 – передаточные функции ФЭ, которые

называются собственными при

j i



и перекрестными связями при

j i



, уста-

навливающими связь

- го выхода с

- м входом.

Выражение (14) можно записать в матричном виде:

( ) ( ) ( )

Y p W p U p



, (15)

где

1 2

( ) [ ( ) ( ) ( )]

Y p Y p Y p Y p





1 2

( ) [ ( ) ( ) ( )]

U p U p U p U p





;

( )

W p l m

 

- передаточная матрица с элементами

( )

W p

На структурной схеме выражение (15) представляется одним из много-

мерных блоков, изображенных на рис. 13.

Рис. 13

Многомерные блоки также могут иметь различные соединения как и од-

номерные блоки. При определении эквивалентных передаточных матриц ис-

пользуются матричные операции и их свойства. Например, для обобщенной

структурной схемы вида рис. 5, где

g y

– вектора размерности



вектор, матрицы

ос

соответствующих размеров, также получим

уравнения (6). Исключая промежуточный вектор



размерности

, найдем вы-

ражение для вектора выхода





2 1 ос 2 1 2

E W WW y W W g W W f

   , (16)

где

–

l l



- единичная матрица, имеющая отличные от нуля только диаго-

нальные элементы, равные единице. Отсюда получим выражение

yg yf

y W g W f

 

или

( ) ( ) ( ) ( ) ( )

yg yf

Y p W p G p W p F p

 

, (17)

где

 

2 1 ос 2 1

( ) ( ) ( ) ( ) ( ) ( )

yg l

W p E W p W p W p W p W p



  ,

 

2 1 ос 2

( ) ( ) ( ) ( ) ( ) ( )

yf l

W p E W p W p W p W p W p



  .

Найдем характеристическое уравнение системы (16). Для этого в уравне-

нии (16) положим



и получим уравнение в изображениях Лапласа:





( ) ( ) 0

E W p Y p

 

, (18)

где

2 1 ос

( ) ( ) ( ) ( )

W p W p W p W p



Уравнение (18) выполняется, если

( )

| ( )| 0

( )

D p

E W p

d p

  

. (19)

Тем самым уравнение

( ) 0

D p



является характеристическим уравнени-

ем, от корней которого зависит свободное движение

( )

y t

Для задания в системе MATLAB передаточных матриц можно использо-

вать команду, формирующую массив одномерных передаточных функций. На-

пример, при заданных элементах передаточной матрицы

11 12

21 22

( ) ( )

( )

( ) ( )

W p W p

W p

W p W p

 



 

 

можно воспользоваться командой W=[W11 W12;W21 W22]

Для определения корней характеристического уравнения

( ) 0

D p



(19)

используется команда tzero(eye(l)+W)

Вопросы для самопроверки

1. В чем отличие эквивалентных передаточных функций для последовательного

и параллельного соединения передаточных функций?

2. Чем отличаются передаточные функции замкнутой системы при отрицатель-

ной и положительной обратной связи?

3. В чем смысл эквивалентных преобразований структурных схем?

4. Как определяется характеристическое уравнение одномерной системы?

5. Какую роль играют корни характеристическое уравнение системы?

6. В чем отличие передаточной матрицы от передаточной функции?

7. Всегда ли можно использовать эквивалентные преобразования для много-

мерных систем?

8. Как определяется характеристическое уравнение многомерной системы?

ЛЕКЦИЯ 7

Представление системы в переменных состояния. Способы построения решения. Пе-

реход от сигналов вход-выход к переменным состояния. Блочные системы в переменных со-

стояний

1. Представление системы в переменных состояния

Представление ФЭ с помощью передаточных функций позволяет строить

структурные схемы и на их основе получать желаемые передаточные функции

системы. Недостатком такого подхода является требование нулевых начальных

условий для переменных ФЭ. В связи с этим в инженерной практике использу-

ется также подход представления системы в переменных состояния, т.е. в виде

совокупности исходных дифференциальных уравнений ФЭ, приведенных к

системе дифференциальных уравнений первого порядка:

0 0

, ( ) ,

x Ax Bu x t x

y Cx Du

  

 



(1)

где



- вектор состояния;

u m



- вектор входа,

y l



- вектор выхода; матри-

цы

соответствующих размеров. Решение

( )

x t

t t



дифференци-

ального уравнения (1) однозначно зависит от начального условия

( )

x t

и входа

( )

u t

. В связи с этим вектор

( )

x t

называют вектором состояния системы (1),

удовлетворяющего общему определению состояния системы.

Определение. Состояние системы в любой момент времени

– это ми-

нимальное количество информации, которое вместе со всеми входными пере-

менными однозначно определяет поведение системы при всех

t t



2. Способы построения решения

Для определения реакции системы (1) на входное воздействие

( )

u t

ука-

жем способы построения решения

( )

x t

2.1. Метод преобразования Лапласа

Проведем преобразование Лапласа левой и правой части уравнения (1) с

учетом начального условия

(0)

x x



в нулевой момент времени. С учетом

{ ( )} ( )

L x t X p



{ ( )} ( ) (0)

L x t pX p x

 



{ ( )} ( )

L u t U p



, для уравнения (1) полу-

чим





( ) (0) ( )

pE A X p x BU p

   .

Отсюда найдем выражение изображения для оригинала

( )

x t

   

1 1

( ) (0) ( )

n n

X p pE A x pE A BU p

 

    . (2)

Используем свойство обратной матрицы:

 

( )

pE A A p

d p



 



где

( ) | |

d p pE A

 

– полином

-го порядка; ( )

A p n n

 



- матрица алгебраиче-

ских дополнений, элементы

( )

a p



которой определяются как произведение

( 1)

i j



 на определитель матрицы, полученной из матрицы

pE A



, вычеркива-

нием строки

и столбца

. Причем порядок полиномов

( )

a p



не превышает

значения



Тогда выражение (2) можно переписать в виде

1 1

( ) ( ) (0) ( ) ( )

( ) ( )

T T

X p A p x A p BU p

d p d p

 

 

. (3)

С помощью обратного преобразования Лапласа по выражению (3) нахо-

дится оригинал

( )

x t

. При

( ) 0

u t



свободное движение системы зависит от кор-

ней характеристического уравнения

( ) | | 0

p a pd p apE A



    





. (4)

При нулевых начальных условиях

(0) 0



с помощью выражения (2)

найдем изображение вектора выхода

( ) ( ) ( )

Y p W p U p



где

( )

W p l m

 

- передаточная матрица определяется по формуле

 

( )

W p C pE A B D



  

(5)

Из выражения (2) согласно теореме о свертке следует выражение для

оригинала

( ) ( ) (0) ( ) ( )

x t t x t Bu d

  

    



(6)

где

 





( )

t L pE A



   называется переходной матрицей состояния (фун-

даментальная матрица), причем первое слагаемое определяет свободной дви-

жение, а второе слагаемое вынужденное движение системы (1).

2.2. Метод разложения в бесконечный ряд

Из выражения (6) следует, что решение

( )

x t

зависит от матрицы

( )



которую можно искать независимо от входного сигнала

( )

u t

. Поэтому в урав-

нении (1) положим

( ) 0

u t



. Найдем решение однородного уравнения

0 0

( ) ( ), ( ) ,

x t Ax t x t x

 



(7)

полагая

t t t

  

. Решение

( )

x t t

 

разложим в ряд Тейлора относительно

начального значения

( )

x t

2 ( )

0 0 0 0

1 1

( ) ( ) ( ) ( ) ( )

2! !

k k

x t x t x t t x t t x t t

        

 

 

(8)

Учитывая, что

0 0

( ) ( )

x t Ax t





0 0 0

( ) ( ) ( )

x t Ax t A x t

 

 

, …,

( )

0 0

( ) ( )

k k

x t A x t

 вы-

ражение (8) перепишем в виде

( ) ( ) ( )

x t t x t

  

(9)

где

2 2

1 1

( ) ... ...

2! !

k k A t

t E A t A t A t e



            , (10)

т.е. переходную матрицу можно считать матричной экспонентой.

Тем самым выражение (10) определяет способ вычисления матрицы

( )



Путем подстановки нетрудно убедиться, что решение (9) удовлетворяет

уравнению (7):

2 1

0 0

1 1

0 0

( ) ( ) ( ) ... ... ( )

2! !

... ... ( ) ( ) ( ) ( ).

( 1)!

k k

x t t x t A A t A t x t

A E A t A t x t A t x t Ax t



 

 

          

 

 

 

          

 



 



Отсюда следует свойство 1 переходной матрицы:

( ) ( )

t A t

    



(11)

Поскольку выполняется равенство:

0 0 0

( ) ( ) ( ) ( ) ( ) (0) ( ) (0)

x t t x t t t t x t x

        

то, очевидно, что для произвольных начальных условий

(0)

выполняется

свойство 2

0 0

( ) ( ) ( )

t t t t

    

(12)

или

0 0

( )

A t t At

e e e





С помощью формулы (12) решение (6) можно записать для начальных ус-

ловий в произвольный момент времени:

0 0 0 0

0 0 0

0 0

( ) ( ) (0) ( ) ( )

( ) ( ) (0) ( ) ( ) ( ) ( ) ( )

( ) ( ) (0) ( ) ( ) ( ) ( )

( ) ( ) ( ) ( ) .

x t t x t Bu d

t t t x t t t Bu d t Bu d

t t t x t Bu d t Bu d

t t x t t Bu d

  

     

  

     

            

 

 

          

 

 

     



 



2.3. Метод преобразования подобия

Из теории матриц известно, что если характеристическое уравнение

( ) | | 0

p a pd p apE A



    





имеет различные корни



 (собственные значения матрицы A) кратно-

сти

(

...

n n n



  

), то с помощью подобного преобразования

| | 0



любую вещественную матрицу

можно привести к блочно диагональной

форме Жордана [12]:





( )

j i

A MJM diag J p



  , (13)

где

( )

j i

J p

–

j j

i i

l l



- жордановый блок вида

1 0 0

0 1 0

( )

0 0 0

j i

J p

 

 



 

 



   



причем

i i

n l





– число жордановых блоков для корня

Тогда формулу (10) с учетом свойства

2 1 1 2 1

A MJM MJM MJ M

  

 

можно записать в виде

2 2 1 1

1 1

( ) ... ...

2! !

k k J t

t M E J t J t J t M Me M

  

 

           

 

 

. (14)

1) В частном случае, когда



, ( )

j i i

J p p



и матрица

является диа-

гональной. Тогда с учетом свойств диагональных матриц матричную экспонен-

ту

J t



можно представить в виде:

{ }

p t

J t

e diag e





Для данного случая с помощью представления матриц

1 2

[ ]

M m m







 

 



 

 



формулу (14) можно переписать в виде

( )

p t

J t

t Me M Qe



 



   



(15)

где

i i i

Q m n n n

  

- матрицы. Тогда решение однородной системы (7) при



(0)

i i

c Q x



запишется в следующей форме

1 1

( ) ( ) (0) (0)

i i

n n

p t p t

i i

x t t x Qe x e c

 

   

 

, (16)

2) В общем случае, когда



, решение

( )

x t

представляется в виде ана-

логичном (16), содержащем слагаемые с множителями

p t

e t

, …,