Гаркушенко В.И. Лекции по ТАУ
Подождите немного. Документ загружается.


51
( ) ( 1)
0 1
( ) ( 1)
0 1
( ) ( ) ( )
( ) ( ) ( ),
n n
n
m m
m
a y t a y t a y t
b u t bu t b u t
(20)
которому при нулевых предначальных условиях соответствует уравнение в изо-
бражениях Лапласа
( ) ( ) ( )
Y p W p U p
, (21)
с передаточной функцией
1
0 1
1
0 1
( )
( )
( )
m m
m
n n
n
b p b p b
m p
W p
d p
a p a p a
, (22)
где выполняется условие
m n
физической реализуемости системы.
Подадим на вход системы гармонический сигнал
( ) cos
m
u t u t
, который
с помощью формулы Эйлера
cos sin
j t
e t j t
можно представить в виде
1 2
( ) ( ) ( )
2
j t j t
m
e e
u t u u t u t
,
где
1
( ) /2
j t
m
u t u e
,
2
( ) /2
j t
m
u t u e
.
Найдем отдельно реакции системы
1
( )
y t
и
2
( )
y t
на составляющие
1
( )
u t
и
2
( )
u t
. Тогда реакция линейной
( )
y t
системы на
( )
u t
равна сумме реакций:
1 2
( ) ( ) ( )
y t y t y t
.
При подаче на вход системы (20) сигнала
1
( )
u t
на выходе возникает пере-
ходной процесс
1
( )
y t
, который содержит переходную и установившуюся со-
ставляющие движения. Если переходное движение со временем затухает, то на
выходе системы установятся вынужденные гармонические колебания. Для их
определения установившееся решение будем искать в виде
1 1 1
( ) ( )
y t Au t
, кото-
рое подставим в уравнение (20). С учетом равенств
(1)
1
1
( ) ( ) /2 ( ) ( )
j t
m
u t j u e j u t
,
( )
1
1
( ) ( ) ( )
i i
u t j u t
,
( )
1 1
1
( ) ( ) ( )
i i
y t j Au t
из
уравнения (20) найдем
1 1 1
( ) ( ) ( ) ( )
d j Au t m j u t
.
Отсюда следует, что
1
( )/ ( ) ( )
A m j d j W j
. Функцию
( )
W j
ком-
плексного переменного можно представить как в декартовой

52
( ) ( ) ( )
W j U jV
, (23)
так и в полярной системе координат
( )
( ) ( )
j
W j A e
, (24)
где
2 2
| ( )|
( ) | ( )| ( ) ( )
| ( )|
m j
A W j U V
d j
, (25)
( )
( )
( )
V
arctg k
U
,
0,1,2,..
k
(26)
С помощью выражения (24) решение
1
( )
y t
можно записать в виде
( ) ( ( ))
1
( ) ( ) /2 ( ) /2
j j t j t
m m
y t A e u e A u e
.
Для определения вынужденного решения
2
( )
y t
на входной сигнал
2
( ) /2
j t
m
u t u e
воспользуемся следующим свойством: в силу равенств
1
j j
и
( )( ) 1
j j
все операции над комплексными выражениями будут
сохраняться с точностью до знака при замене
j
на
j
. В силу данного свойства
решение
2
( )
y t
будет иметь вид
( ( ))
2
( ) ( ) /2
j t
m
y t A u e
.
Тогда окончательно получим
( ( )) ( ( ))
1 2
( ) ( ) ( ) ( ) ( ) cos ( )
2
j t j t
m m
e e
y t y t y t A u A u t
.
Таким образом, на выходе системы устанавливаются вынужденные гар-
монические колебания с амплитудой
( )
m m
y A u
, частотой
и фазовым
сдвигом
( )
относительно входного сигнала. При этом
( )
A
,
( )
зависят от
частоты
и вида передаточной функции
( )
W p
и не зависят от амплитуды
m
u
входного сигнала. Отсюда следует методика экспериментального определения
характеристик
( )
A
,
( )
:
1. С генератора синусоидальных колебаний на вход исследуемого объекта
подаётся гармоническое воздействие заданной частоты
и произвольной, но
допустимой по величине амплитуды
m
u
.
53
2. После завершения переходного процесса измеряют амплитудные зна-
чения колебаний на выходе
m
y
исследуемого объекта.
3. По осциллографу определяют разность в фазах выходных и входных
гармонических колебаний, выражают её в градусах или радианах и получают
аргумент
( )
.
4. Вычисляют модуль частотной характеристики по формуле
( ) /
m m
A y u
.
5. На генераторе изменяют частоту гармонических колебаний и для ново-
го её значения повторяют всю процедуру, начиная с п.1.
Графики функций
( )
A
и
( )
при изменении
0
называются ам-
плитудно-частотной характеристикой (АЧХ) и фазовой частотной характе-
ристикой (ФЧХ) соответственно.
График функции
( )
W j
, построенный на комплексной плоскости при
изменении
0
, называется амплитудно-фазовой частотной характери-
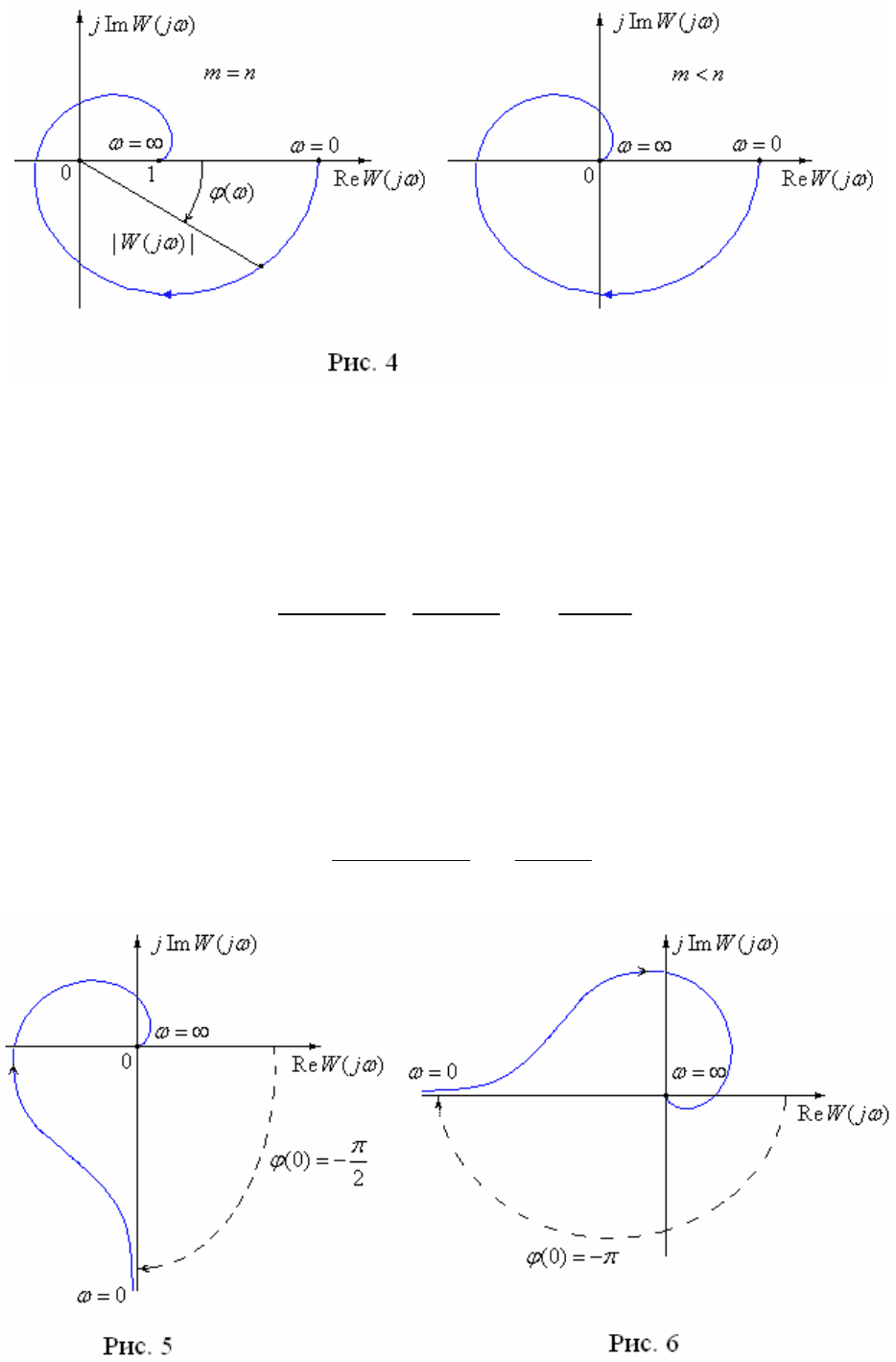
стикой (АФЧХ) (рис. 4). Очевидно, что по известным характеристикам
( )
A
и
( )
можно построить характеристику
( )
W j
и наоборот.
5. Свойства АФЧХ.
Рассмотрим свойства АФЧХ физически реализуемых систем с передаточ-
ной функцией (22).
1) При
0
АФЧХ начинается на вещественной оси (рис. 4):
( 0) /
m n
W j b a
при
0
n
a
.
2) При
АФЧХ заканчивается на вещественной оси (рис. 4):
0 0
/ при ,
( )
0 при .
b a m n
W j
m n
54
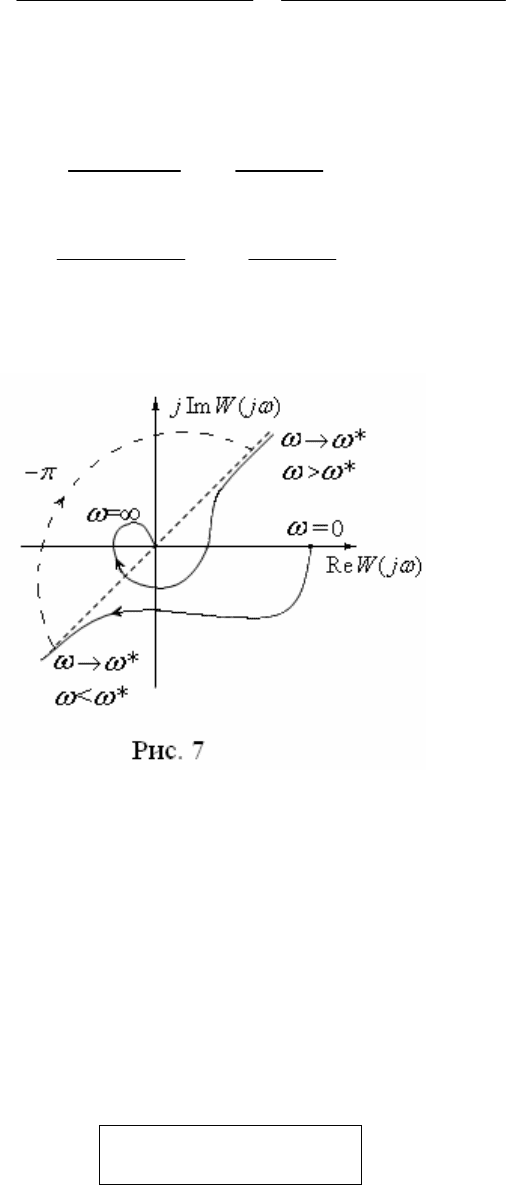
3) Если
0
n
a
, то при
0
АФЧХ имеет значение
( 0)
W j j
и
(0) /2
(рис. 5). Действительно в этом случае
( ) ( )
d p pd p
и при
0
m
b
получим
1 1
( 0)
( 0)
0 0
0 ( 0)
m m
n n
b bm j
W j j j
j a a
j d j
.
4) Если
0
n
a
,
1
0
n
a
, то при
0
АФЧХ имеет значение
( 0)
W j
и (0)
(рис. 6). Действительно в этом случае
2
( ) ( )
d p p d p
и при
0
m
b
получим
2
2
( 0)
( 0)
0
( 0) ( 0)
m
n
bm j
W j
a
j d j
.
55
Таким образом, если уравнение
( ) 0
d p
имеет
нулевых корней, то на-
чальное значение фазы
(0) /2
.
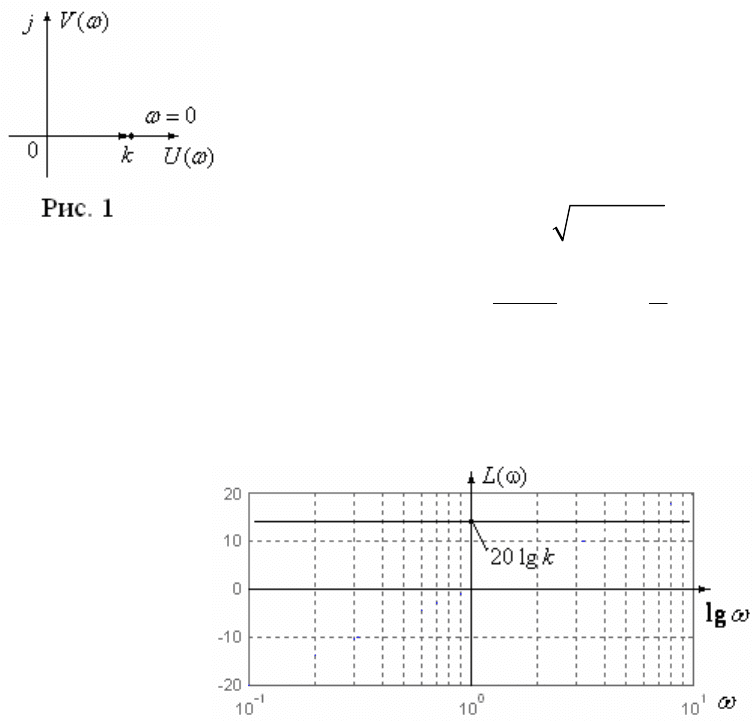
5) Если
2 *2
( ) ( ) ( )
d p p d p
, то при
*
АФЧХ имеет разрыв второ-
го рода (рис. 7). Действительно в этом случае получим
2 *2 2 *2
( ) ( )
( )
) ( 0) ( )
(
m j m j
W j
j d j d j
.
Тогда при
*
будем иметь:
* *
*
* *
*
* *
*
* *
( ) ( )
= при ;
0 ( ) ( )
( )
( ) ( )
=- при .
0 ( ) ( )
m j m j
d j d j
W j
m j m j
d j d j
Таким образом, при
*
значение фазы скачком меняется на
.
6. Логарифмические частотные характеристики и их свойства.
В инженерной практике широкое применение получили логарифмические
частотные характеристики (ЛЧХ), отличающиеся от предыдущих частотных
характеристик масштабами представления.
Логарифмическая амплитудная частотная характеристика (ЛАХ) оп-
ределяется по формуле
( ) 20lg ( )
L A
.
(27)

56
Единицей измерения по оси ординат является децибел (дБ), заимствован-
ный из акустики, единицей деления является 20 дБ. Логарифмическая фазовая
частотная характеристика (ЛФХ)
( )
по оси ординат строится в равномер-
ном натуральном масштабе с единицей деления
/ 4
. Общий для ЛАХ и ЛФХ
параметр – частота откладывается в логарифмическом масштабе
*
lg( / )
, ха-
рактеризующем изменение частоты относительно базовой частоты
*
. Единица
десятикратного изменения частоты называется декадой. Значение
*
определя-
ет начало координат в логарифмическом масштабе и может назначаться произ-
вольно. В системных исследованиях обычно
*
1
рад/с, в экспериментальных
условиях удобно начало координат связать с началом частотного диапазона ге-
нератора синусоидальных колебаний.
Таким образом, ЛАХ (27) является полностью логарифмической как по
оси ординат, так и по оси абсцисс, а ЛФХ является полулогарифмической. При
построении ЛЧХ по экспериментальным данным их преимущества никак не
проявляются. Более того, необходимы дополнительные вычисления по формуле
(27) и вычисление координат по оси абсцисс по формуле
* *
lg lg
f
f
,
где
2
f
,
f
– частота в герцах (Гц). Однако, только в логарифмических
масштабах возможно однозначное восстановление фазовой характеристики для
минимально-фазовых систем по логарифмической амплитудной характеристи-
ке. Это исключает необходимость измерения
( )
, что существенно упрощает
эксперимент.
Рассмотрим свойства ЛАХ и ЛФХ для произвольной передаточной функ-
ции (22). Для этого найдем корни полинома числителя (нули) и корни полинома
знаменателя (полюса) передаточной функции и согласно теореме Безу полино-
мы числителя и знаменателя передаточной функции (22) представим в виде
произведения простейших множителей:

57
2 2
1 1
2 2
1 1
1 2 1
( )
( )
( 1) ( 2 1)
i i i i
i i
v
i i i i
i i
k p p p
m p
W p
d p
p T p T p T p
. (28)
Здесь множители
1
i
p
соответствуют вещественным корням, а множители
2 2
2 1
i i i
p p
при
0 1
i
комплексно-сопряженным корням уравнения
( ) 0
m p
. Множители
( 1)
i
T p
и
2 2
( 2 1)
i i i
T p T p
при
0 1
i
соответствуют
вещественным и комплексно-сопряженным корням уравнения
( ) 0
d p
соот-
ветственно. Множители
v
p
соответствуют нулевым корням знаменателя при
0
v
и числителя при
0
v
. Коэффициенты
i
и
i
называются коэффициен-
тами демпфирования.
Таким образом, передаточную функцию (28) можно представить в виде
произведения типовых передаточных функций:
1
( ) ( )
N
i
i
W p W p
, (29)
где типовые передаточные функции
( )
i
W p
приведены в таблице 1.
Таблица 1.
№ Название типового звена Передаточная
функция
Нули /полюса
1. Безинерционное звено
k
2. Дифференцирующее звено
p
1
0
p
3. Интегрирующее звено
1
p
1
0
p
4. Форсирующее звено первого
порядка
1
Tp
1
1/
p T
5. Апериодическое звено
1
1
Tp
1
1/
p T
6. Форсирующее звено второго
порядка
2 2
2 1
T p Tp
2
1,2
/ 1 /
p T j T
7. Колебательное звено
2 2
1
2 1
T p Tp
2
1,2
/ 1 /
p T j T

58
Название типовых звеньев следует из вида их переходных характеристик
[1], поведение которых зависит от нулей и полюсов передаточной функции:
дифференцирующее и интегрирующее звено осуществляют дифференцирова-
ние и интегрирование входного сигнала соответственно; выход апериодическо-
го звена имеет монотонно нарастающий процесс, не превышающий установив-
шегося значения; выход колебательного звена имеет затухающие колебания от-
носительно установившегося значения (см. лекция 11).
Представленные в таблице 1 звенья с положительными коэффициентами,
у которых нули или полюса имеют отрицательные вещественные части, назы-
ваются минимально-фазовыми. В таблице 2 приведены неминимально-фазовые
звенья с отрицательными коэффициентами, у которых нули или полюса имеют
положительные вещественные части.
Таблица 2.
№ Название типового звена Передаточная
функция
Нули /полюса
1. Неминимально-фазовое форси-
рующее звено первого порядка
1
Tp
1
1/
p T
2. Неминимально-фазовое аперио-
дическое звено
1
1
Tp
1
1/
p T
3. Неминимально-фазовое форси-
рующее звено второго порядка
2 2
2 1
T p Tp
2
1,2
/ 1 /
p T j T
4. Неминимально-фазовое колеба-
тельное звено
2 2
1
2 1
T p Tp
2
1,2
/ 1 /
p T j T
Подставим в (29)
p j
и получим частотную передаточную функцию
1
( ) ( )
N
i
i
W j W j
(30)
С учетом выражения (24) можно записать
1
1
( )
(
1
)
( )
( ) ( ) ( ) ( )
N
i
i i
N
j
j
j
i
N
i
i
i
W j A e A e A e
.
Отсюда следуют формулы

59
1
( ) ( )
N
i
i
A A
,
(31)
1
( ) ( )
N
i
i
.
(32)
Переходя к логарифмической амплитудной частотной характеристике по-
лучим выражение
1
1
( ) 20lg ( ) 20lg ( ) 20lg ( )
i i
N
N
i
i
L A A A
.
Тем самым справедлива формула
1
( ) ( )
N
i
i
L L
,
(33)
т.е. ЛАХ произвольной передаточной функции равна сумме ЛАХ типовых
звеньев.
Таким образом, для построения ЛАХ передаточной функции необходимо
знать ЛАХ типовых передаточных функций, приведенных в таблицах 1,2.
Вопросы для самопроверки
1. При каких условиях строятся временные характеристики?
2. В чем отличие переходной и весовой характеристик?
3. Как связаны переходная и весовая характеристики?
4. С помощью какой характеристики можно построить реакцию системы на
произвольное входное воздействие?
5. Какой физический смысл имеют АЧХ и ФЧХ системы при подаче на ее
вход гармонического сигнала?
6. Какие передаточные функции называются типовыми?
7. В чем отличие АЧХ и ЛАХ, ФЧХ и ЛФХ?
8. Каким свойством обладает ЛАХ передаточной функции?
60
ЛЕКЦИЯ 5
Частотные характеристики типовых передаточных функций. Методика построе-
ния ЛАХ и ЛФХ.
1. Частотные характеристики типовых передаточных функций
Рассмотрим свойства частотных характеристик типовых звеньев, приве-
денных в таблице 4.1. Для каждого звена проведем построение АФЧХ и соот-
ветствующих ЛАХ и ЛФХ.
1.1 Безынерционное (усилительное) звено
1) Для построения АФЧХ в передаточную функцию подставим
p j
и
выделим вещественную и мнимую часть:
( ) ( ) ( )
W j k U jV
.
Отсюда следует, что
( )
U k
,
( ) 0
V
. На рис. 1 приведен график АФЧХ в
виде точки на вещественной оси. При этом из графика
видно, что при изменении
0
ФЧХ равна нулю.
2) Для построения ЛАХ и ЛФХ воспользуемся
формулами
2 2
( ) | ( )|
A W j U V k
,
( ) 0
( ) 0
( )
V
arctg arctg
U k
.
Отсюда следует, что ЛАХ
( ) 20lg
L k
, построенная в логарифмическом
масштабе
lg
имеют вид рис. 2, а ЛФХ
( ) 0
.
Рис. 2
