Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

236

Transient

flow

in

gas

pipe

networks

lch.

11

e +P:

r

.P:

C-T

p

"l-

tp

where

Qo

is

the specific

heat

at

constant

pressure.

The total

heat

is known

as

the

enthalpy

and

is

CpT

+ u2l2.I*tthe

perimeter

of the

gas

element

be

s and

the rate

of

heat

inflow

to

the

system

be

q

units

of

heat per

unit

area.

The

heat

inflow

to the

Sec.

11.41

The

value

of

g

237

where

m is

the

hydraulic

mean

radius

of

the

duct.

6Al0x

is the

rate of

increase

in

the

area

of the

duct.

In

a

parallel-sided

duct,

OAIOx:

0.

These

forms

of equation

are

due

to G.

Edgell

[20].

ll.3.l

The use

of

the

characteristic

equations

Along

RP in

Fig.

11.1,

equation

(11.4)

applies

and

is a

forward

or

positive

Fig.

11.1

-The

wave

and

particle

paths.

I1.4

TIIE

VALI'E

OF

g

q

is

the

rate of

inflow

of

heat

per

unit area

of

pipe

wall

per

unit

of time

(Fig.

11.2).

euasi-steady

heat

flows

into

the

pipe

may

be assumed

with little

resulting

error;

so

the standard

heat

inflow

methods

oianalysis

may be

used.

The error

in this

approach

lies in

the

fact that

this

analysis

ignores

the

heat needed

to raise

or

lower

the

pipe

wall

material

through

any

required

temperature

rise or

fall.

Newton's

law

of

heat

transfer

can

be

used,

i.e.

q=cLT"

where

A?.

is the

temperature

difference

across

the

wall.

In steady

state,

*

e.,9)

-,+x(#.,#)

-tr-f

=

o

(11.3)

(11.4)

(11.5)

(11.6)

(11.7)

(11.8)

(11.e)

11.3

THE

CHARACTERTSTIC

EQUATTONS

The

characteristic

equations

are

**!-*=

u,

along

ot

Tp

dt

*-:*=

u,

arong

\r,

YP

ut

#-

**:

t,

arong

d-r

::u+c

dt

d.r

::0-c

ot

dx

-=u

dt

where

u,:Th.#(ry-')

-on#,

Es:(^t_r(***)

T-l

q

-#(ry+r)

+oo#

Ez:

cpm

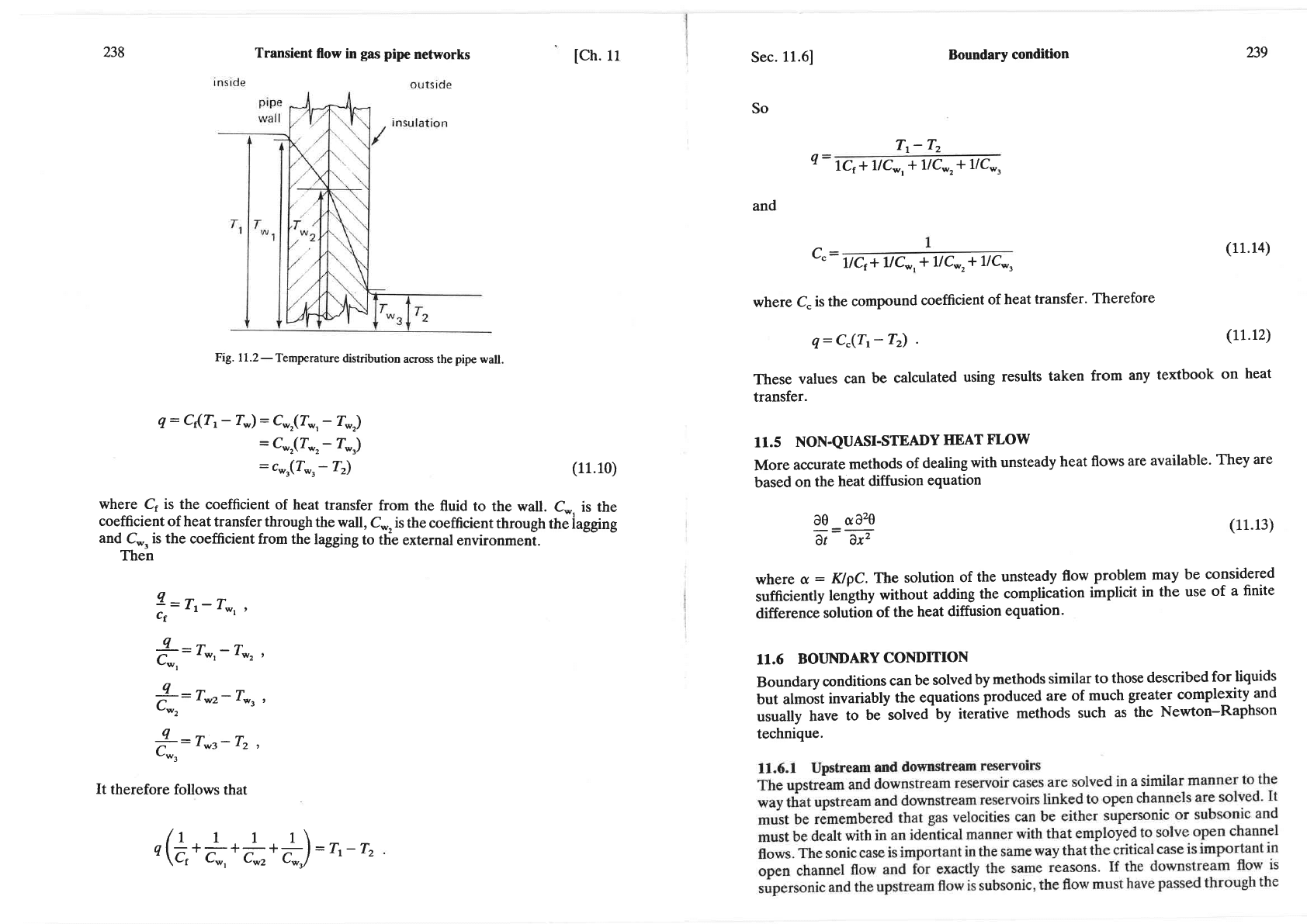
238

Transient

flow

in

gas

pipe

networks

Fig.

11.2-Temperature

distribution

across

the

pipe wall.

Q:c{r'-&)

=?tfr'"-t'l

c*r(r*,

-

Tr)

lch.

11

(11.10)

Sec.

11.61

So

Boundary

condition

239

(11.14)

(11.13)

Tr-

T,

q:

1Cf

+ uC*,+

llc*,+

llc*,

and

c.:

Llcr+

yc*,+

Llc*,+

Llcn,

where

C.

is the

compound

coefficient

of

heat

transfer.

Therefore

Q:

C.(Tr-

Tr)

.

(L1"12)

These

values

can

be

calculated

using

results

taken

from

any

textbook

on

heat

transfer.

11.5

NON-QUASI-STEADY

ImAT

FLOW

More

accurate

methods

of

dealing

with unsteady

heat

flows

are

available.

They

are

based

on

the

heat

diffusion

equation

A0

c04

-___

Ot lxz

where C, is

the coefficient

of heat

transfer

from

the

fluid to

the wall.

C*, is the

coefficient

of heat

transfer through

the wall,

C*, is

the coefficient

through

the iagging

and

C*,

is the

coefficient

from the

lagging

to the

external

environment.

Then

1:r'-T*,

'

Q

_T

4:

l*' T*'

'

Q

_T

(-

^

*z-

T*t

,

vw-

i:r*s-rz,

u*.

It

therefore

follows

that

where

s

:

KlpC.

The

solution

of

the

unsteady

flow

problem

may

be

considered

sufficiently

lengthy

without

adding

the

complication

implicit

in

the use

of

a finite

difference

solution

of

the

heat

diffusion

equation-

11.6

BOTJNDARY

CONDITION

Boundary

conditions

can

be

solvedby

methods

similar

to

those

described

for

liquids

but

almost

invariably

the equations

produced

are

of

much

greater

complexity

and

usually

have

to

be solved

by

iterative

methods

such

as the

Newton-Raphson

technique.

,(i,.+.**+)

=r,-rz

240

Transient

flow

in

gas

pipe

networks

lch.

11

sonic

case.

If this

happens,

the local velocity

is

equal

to

the wave

speed

and

the

conditions downstream

cannot

affect

the conditions

upstream

in

exactly the

same

way that

downstream

supercritical

conditions

in an

open

channel

cannot

affect

upstream

subcritical conditions.

Bearing

these

arguments

in

mind

and remembering

that there

is a

particle

path

along which

information

is carried

in

the case

of

gas

flows,

the two

reservoir

cases can

be solved

by

similar

methods

to

those

used in

the

open

channel cases.

11.6.2 Turbo-blowers

or compressors

These act

in exactly the

same

way

as do pumps

in the

case

of liquids

and

can

be

handled in

a surprisingly

similar

manner.

The

energy

per

unit

weight

supplied to

the

gas

is

given

by the

equation

H:ANz+BNQ_CQ'

Sec.

11.91

Shocks

Polytropic

indices

for

a compressor

may

be

as

large as

5.3

because

of these

large

losses and

cun

be obtained

either

from

the

literature

orfrom

the following

equation:

241

H:Rrr+l-(+)'"-""-

t1

n-

lL\P'l

I

together

with

n-t_Y-11

nyep

(1

1.1s)

(11.16)

where

Q

is

the flow in

cubic

metres

per

second at inlet pressure

and temperature.

The

Il

versus

Q

cuwe is

supplied

by the

manufacturer

in the

same way

that

the

pump

manufacturer

supplies the

.F/

versus

Q

cuwe

for a

pump.

The ^Fl

versus

Q

curve is

a

statement about angular momentum;

so it is

not surprising

to find

that it

works

perfectly

as

well

for

gases

as for

liquids.

This

statement

must be

qualified

as

compressors can

surge. The

explanation

of this is that

the rotating

blades

can

be

thought

of

as resembling

aerofoils

which

can become

stalled

if the

compressor

is

exposed to

too high a

pressure

difference

across it

(Fig.

11.3).

This

causes the

flow

to

{a)

(b)

Fig.

I 1.3

-

(a)

Normal H

versus

Q

curve;

(b)

F/ versus

Q

curve with

stalled blades.

separate from

the blading

and additional,

heavy

energy

losses

are then generated

which distort

the head

versus

flow characteristic

of the

compressor.

One

way

that the

pressure

difference

across

the compressor

can

be calculated,

given

that

the.Flvalue

has been

evaluated

from

the Flversus

p

relationship

allowing

for any

stalling

of the blades,

is based

on the assumption

that the

flow through

the

compressor

is following a

polytropic

process.

(Note

that adiabatic

processes

are not

applicable

to

a compressor as

there

are

significant

energy

losses

occurring within

it.)

where

eo is

the

polytropic

efficiency

of

the

compressor.

The

polytropic

efficiency

must,

of .o,16",

be

known

or

be able

to be estimated

from

II.7

THE

COMPRESSIBILITY

COEFFICIENT

common

practice.

11.8

JTJNCTIONS

Readers

are

warned

that

junctions

exhibit

all

the

problems that

are

found

in

open

channel

junctions.

If

all the

pipes

joining

at

a

junction

are

running

subsonically,

a

technique

similar

to

the

one

illustrated

for

subsonic

open

channels

will

work, but

it

must

be

remembered

that

mass

flow

through

the

junction

is

conserved

and

not

1r.9 SHOCKS

The shock

is

analogous

to

the hydraulic

jump

in open

channel

flows

and

the moving

shock

is analogouJto

the

travelling

surge.

Again,

if it

is

remembered

that

mass

is

conserved

and

not

volume,

the methods

used

for travelling

surges

can be

adapted

to

deal

with

shocks.

The equation

for

a normal

shock

is

given in

all

textbooks

on

gas

dynamics

and

in some

general

fluids

texts.

As stated

before

in the

section

on

open

channel

flow,

it is

required

that

the

relative

Froude

numbers

must

span

unity,

and

similarly

here

the relitive

Mach

numbers

across

the

shock

must

also

span

unity.

(11.14)

curve when

are

stalled

12

The

programming

of the

wave

equations

I2.1 INTRODUCTION

This entire book

is

of only academic

interest

if

the reader

has

no access

to

a

computer. The

integration

of

the

wave

equations

involves

massively

heavy

compu-

tation. This can

only be

performed

if a computer

of

adequate

speed

and

sufficient

storage is available.

Only then can

networks

of

significant

size

and complexity

be

analysed. The

author

recommends

a microcomputer

equipped

with

a

80286 chip

and

a random-acces

memory

of at least

256 kbytes

together

with

an

80287

mathematical

coprocessor. The

language

in which

the

program

is written

could

be

any

of the

modern languages

such as Pascal,

C,

Fortran

or

one

of the modern

fast versions

of

Basic. Modern

versions

of Fortran

have their

attractions

and the user

may

contem-

plate

using Fortran

77 butthe

author

finds that

the language

for whieh

a eompiler

is

most commonly

available

is Fortran

IV. For

this reason

the following

description

of

how to write a

suitable

program

is based

on Fortran

IV.

Any

problem

that

the reader

may

be called

upon to

analyse

could be

dealt with

by

writing

a specific

program

for

it. This

approach

has

its attractions

but the

author

strongly recommends

the

reader

to face

the

much

larger

challenge

of

writing

a

program

that

will

solve any

network without

modification.

Any

scheme can

then be

analysed, however

complex.

In

the author's

experience

such a

program

will

never

be

completed, however,

and the first

'simple'

general

program

that

the

programmer

develops will

not

be

quite

sufficient to handle

the

that

he is

called

upon

to

solve. He will

add to

it and may

reach a

stage when

the

program

appears

capable

of

solving

all

problems

presented

to it, but,

sooner

or later,

a

problem

will

arise which

it

is

not

quite

capable

of

handling

and

so

will

need

further

development.

Most

large

general

programs

behave like

this, however.

I2.2 THE

OVERALL PHILOSOPHY

OF THE

PROGRAM

The

programmer

must

provide

a

way

by which

the

user can

define

the network

and

the

directions in which

the

fluid moves

through

it.

The user will

have a

schematic

Sec.

12.31

The

description

of

network topology

243

drawing

of

the

network

and

will,

undoubtedly,

be able

to say

in which direction

he

expectJ

the

fluid

to move,

at

least

when

in steady

state.

It

does not

matter

if

he

guLrt"t any

direction

wrongly

as

will

be seen

later. In effect

it

is necessary

to

define

*tti.tt

end

of

any

pipe

is

the

upstream

end

and

which is

the

downstream

end. To

do

this

job,

systematically

insert

arrows

on

the

schematic

diagram

of

the

network,

poiniing in the

expected

direction

of

flow.

The end

towards

which the

arrow

points

is

ihe

downstream

end

and the

other

end

is

the upstream

end.

The importance

of

the

definition

of

the

pipe

ends

is

that the

numbering

of the

Ax

nodes

starts

at I'

at the

upstredm

end

and

is

netno(i)

at

the

downstream

end.

i

is here

used

to

denote

the

nlmber

of

the

pipe which is being

considered.

If

the

procedure

is not

carried

out

correctly

and

the

direction

of

steady

flow

is

wrong on

a

given

Pipe,

the

velocity

of

flow

will be

bbtained

with a negative

value

indicating

that the

flow is in

the

opposite

direction

to the

one

guessed.

The

program should

consist

of

a main

segment

which

calls

an input

subroutine,

then

calis

ail

the required

subroutines

for

the

various

hydraulic

calculations,

then

calls

an

output

roufine

which

sends

the

required

calculated

values to

whichever

output

device

is chosen,

and

finally,

returns

control

to

an earlier

stage

of the

program

so

that

the

hydraulic

calculations

can

be

performed again.

This

process must

be

repeated,

the

time

appropriate

to

the

calculation

advancing

progressively

by

an

amount

of

Aruntil

the time

to

be simulated

is exceeded.

The

program then

must

stop.

Additionally

titles

must be

output

to the

printerwhen

required.

It is

advisable

to

use

subroutines

for every

function

required

in

the main

segment

as this

provides

easy

location

of error.

The

remainder

of

the

program

will

consist

of

the subroutines.

The

fundamental

diffeiences

between

a

general

program and

a

program

written

to solve

a

specific

problem

consist

(i)

in the

way

in

which the

network

topology

is supplied

to

the

program

and

liii

fto* the

iubroutines

are made

to

recognise

that

they

are relevant

to

the

pipe

under

eurrent

examination.

I2.3

TITE

DESCRIPTION

OF

NETWORK

TOPOLOGY

Three

properties

of a

pipe are important

when

considering

a network.

The

first

is the

lengthbf

each

pipe

initr-e

network

as this

decides

how

many

Ax

lengths

are

present in

uny

indit

idual

pipe.

The

direction

in

which

the analyst

thinks

flow is

occurring

in

an

individuat

pipeisitre second

because

this

decision

determines

which end

of

the

pipe is

considereO

to Ue

the

upstream

end,

for

which

the

node counter

will be one,

and

which

is

the downstream

end

for

which

the

node

counter

will be

netno(f).

Netno(n)

is a

one-dimensional

array

which contains

the

number

of

Ax

lengths

in

each

pipe'pinr on".

n is the

number

of

pipes

in

the

network.

Even

if the

analyst

gu6r.rihidirection

of the

flow

wrongly,

no harm

is done

as all

that

will

happen

will

be that

the

velocities

will

be

calculated

with negative

sign.

The

third

property of

any

pipe

consists

of

information

as

to what

is

connected

to

the

pipd

at ea;h

end.'The

way that

this

information

is

supplied

is

in the

form of

two

integei

numbers

although

there

is

no

reason

why it should

not be supplied

in

some

othei

manner.

The

author

suggests

an

array

which he

calls

iroute(n,

2).

There

are

Boundary

condition

Upstream

reservoir

Downstream

reservoir

Junction (upstream)

Junction

(downstream)

Pump

244

The

programming

of the wave

equations

lch.

12

two numbers

for

each

pipe

iroute(i, 1) and

iroute(i,

2) where i

is the

integer number

of the

pipe.

Iroute(i, 1) is

the upstream

end number

and

iroute(i, 2)

is the

downstream

end

number.

These two

numbers

can take

any integer value

and the

prograrnmer

can choose whatever code

he likes

to describe

the various

boundary

conditions.

Here are

a few

numbers

which

could be

used but the

reader can use

anv

others should

he so

wish.

iroute(r,2)

(downstream)

1

2

3I to 34

The integer

numbers forpump are

needed as

procedure

pump

can

be complicated. A

pump

may have an

air

vessel

associated with

it

and/or a valve.

One

way

of dealing

with this

is

to use a simple

pump procedure

with

an air

vessel

one

Ax

downstream

followed

by

a

valve

at an additional

A.r. This works

but

is not

totally accurate

so a

compound

procedure

can be

written.

iroute(i,

1):31

gives

an upstream suction well

pump.

iroute(1,

l):32

gives

an in-line booster

pump

iroute(i,

1):33

gives

an air

vessel

located

just

downstream

of a

suction-well

pump

iroute(i,

1):34

glves

an air vessel

located

just

downstream

of

an in-line booster

-

pump.

This way

of using iroute

allows the first number

3 to define a

pump

and the

second

number

to

define

any additional

circumstance.

Other variants

can

be added to

subroutine pump

as and

when

required.

Air

vessel(downstream)

4I

or

42

iroute(i,

2)=4t

gives

an air

vessel

of constant

cross-section

arranged with its

longitudinal axis vertical.

iroute(i,

2):42

could be

written

for the

case

of an air vessel

with

the shape of a

horizontal

cvlinder.

Valve

5L,52

Again

it will be

seen that

variants

can

be added

to the

subroutine

as and when

required.

iroute(i, 2):51,gives

a

valve

connected

on

either side into

the

network,

the

valve

being

located at the downstream

end of the upstream

pipe.

Valve movement

may be

opening

or closing as required.

iroute(r,

2):52

gives

a

valve

located

at the downstream

end

of a delivery

pipe

to

which

no

pipe

is connected

on the

downstream side

of the

valve.

Surge tank

etc.

iroute(i, 1)

(upstream)

t

2

61

Sec.

12.41

Subroutines

245

It

will be seen

that,

when a

pipe isbeing

analysed

which has

an

iroute(i,

2)

value of32,

a

subroutine

which

performJan

analysis

of

a

pump located

at the

downstream

end

of

the

pipe must

be ialled

to calculate

the heads

and

velocities

of

flow

up

and

downsiream

of the

pump. If

the

value of

iroute(i,

1)

is I

then

subroutine

upstream

resewoir

must

be

ialled

to

calculate

the

head

and

velocity

at the

outlet

of

the

reservoir.

Similarly

each

nurnber

requires

that

a subroutine

be

called

and

these

take

current

values

of

head

and

velocity

and

calculate

from

them

the

values that

will exist

at

the

time

r*Ar.

Some

subroutines

such

as

downstream

pumps and

valves

assume

that

the

pipe

currently

being

examined

are

@nnected

to i

downstream

pipe the number

of

which

is one

nigher

than

that

of

the

current

pipe. This

means

that,

when

the

network

is

being

ntinbered,

it is

necessary

that

pipe numbering

is sequential

across

such

bouridary

conditions.

Reservoiri,

suction-well

pumps

and

other

devices

which

are

located

"t

un

upstream

or

downstream

end

of

the

network

cannot

be

numbered

sequentially

of

course

and

do

not

need

to

be.

Junctions

are

different

from

all

otherboundary

conditionsinthat

they

permit

the

linkage

of any

number

of

pipes of

any

numbering.

Because

of

this

a

particular

pipe

meeti"ng

othei

pipes at the

junction

must

be

selected

at

the

time

of

run

to

receive

an

iroute(l

2) number

of

2.

Additionally

a

group of

integer

numbers

must

also

be

read

in to

an integer

array

called

junct(z,

5)

*[ich

consists

of

the

numbers

of

the

pipes

that

join

at

the

jinctionbut

which

are

assigned

a

plus

or

minus

sign

according

to

whether

ihe

analysithinks

that

the

flow

in

theindividual

pipe is transporting

fluid

towards

or

away

from

the

junction.

If

an error

is

made

in

these

assignments

of

sign,

the

flow

velocity

in

pipei with erroneous

signs

will be

calculated

to

be

negative

but

no

other

error

will

beintroduced.

The

dimensions

of the

array

junct

are

n

and 5.

As

n

is

the

number

of

pipes

in

the

network

this

means

that

any

pipe may

have

a

junction

at

its

downstream

end

and

5-1,

i.e.

4,pipes

may

join

at

these

junctions-

If

the

network

contains

junctions

at

which

more

tlian

four

pipes

meet,

it

will

be

necessary

to increase

this

dimension

to

a

number

equal

to the

largest

number

of

pipes

joining

at

any

junction

plus

one.

The

reason

thlt

the

dimension

irrust

be

greater than

the

rnaximum

number

otpip"r

joining

at

any

junction

by unity

is that

the

first

number

in

the

alray

junct

must6.thtou-U-erof

pipls

joiningitthat

junction,

theremainingmembersof

ih"

"rr.y

being

the signed

numUlrs

of

the

pipes

joining

at

the

junction

as

stated

before.

I2.4

SUBROUTINES

Subroutines

can

take

many

forms

according

to

the style

favoured

by

the

program-

mer.

What

will be

said

about

subroutines

in the

following

paragraphs

reflects

the

author's

taste

and

is not

intended

to

be

authoritative.

Seeing

how

one

person,

the

author,

writes

the subroutines

may

help

the

reader

by

pointing

out

difficulties

and

problems

which

the

reader

has

not

yet

Lncountered.

The

following

ways

of

writing

the

subroutines

is intended

for

guidince

only

and

the

programmer

is

free

to

modify

and

develop

other

ways of

achieving

the same

ends.

The

prograrnming

of the

wave

equations

lch.

12

12.4.1 The input subroutine

INPDAT

This

subroutine is

the most

variable

of all. There are three

ways

of supplying

a

program

with

the

necessary information

i.e., data,

and these

are as follows

(i)

Via

a data file

which is

prepared

by the user of the

program

and

read in at the

time

of

run. This method is the

quickest

and is the most suitable

for batch

operation of the

computer. It is not'user friendly' but it is the best

method for

regular frequent running of the

program.

(ii)

The

programmer

writes

an input subroutine

which

makes

the

program

user

friendly.

This

requires the

programmer

to

generate questions which the

computer

then

writes out to the

visual

display unit for the

user to answer.

The

answers, consisting of numbers or titling

for

graphs,

etc., are then

stored in

the

machine until the

program

is run,

usually

coincidentally,

and are then

used.

This

method

is

welcomed by the user at first and if the

program

is to be

used only

occasionally this

is

a

good

way

of supplying the

data but, if

the

program is to be

used

often,

the

process

of sitting

at a

visual

display unit

and

putting

in a set of

answers

to a lengthy

list

of

questions

can be

very

tedious.

(iii)

By the

use

-

in Fortran

-

of

the data

and

block data facilities.

By

editing the

program

and typing

in the required

data or

block data the

program

is

tailored to

the

specific application

and then

only needs to

be run. However,

this needs

to be

doneevery

time

that theprogram is to be used for a different

application

and the

program

will

have to

be recompiled

every

time. Really, these

facilities

are of

most use when developing the

program

and it

is

necessary

to use test

data over

and

over again

when runs are repeated to locate errors and

make corrections.

The

computer used may affect the

way

in

which

input is

made to a

program

and

the various

compilers

available

for the different languages offer somewhat

different

facilities;

so it is not

possible

to make further comment on

how to

write the input

subroutine.

The following is an example of

a user-friendly input

subroutine

which reads in

data

for

a

program

which dealswith a networkwhich may contain

50

pipes,

junctions

which

may have four

pipes

joining

at the

largest

junction,

50

pumps,

50 air

vessels, 50

valves

and

50 reservoirs.

It

is

probably

needless to say that

it

would

be impossible

to

have

50

pumps

and 50

air

vessels

and valves

and

reservoirs all at

the same

time. The

terms

used

in the common

block have the following meanings.

EL is the

pipe

length.

D

is the

pipe

diameter.

EK

is

the

pipe

roughness.

G

is the

gravity

constant.

W is the

specific weight

of the

fluid. WNU is the kinematic

viscosity

of

the fluid.

Hl. is the total

head

at time /. Vl is the

velocity at time t.HZ is the head

at

time

t+Lt and

V2 is

the

velocity

at time t+At.

QP

is the

flow through

the

pump.

Z is the elevation

of

the

various pipe

nodes above some

arbitrary datum level. DX is

the internodal

space.

IROUTE

contains

boundary condition

control numbers described

above. NETNO

is

the number

of Ar spaces

in any

pipe

length

plus

one. JUNCT

is the

array containing

thesigned

numbers of

the

pipes

joining

at any

junction.

HRES is

the array containing

the

elevations

of the

reservoirs connected

to the network above

the centreline

of

the

pipes

adjacent to the

reservoir.

PI is

3.14159.

HA is the

height of

the water

barometer

(usually

10.3).

HG is the absolute head at

which

water

boils at

normal

temperature (usually

0.1).

El is the fractional

volume

of air

present

in the

water

in

bubble

form.

E2

is

the

fractional

volume

of air

dissolved

in

the

water'

RWSP

is

the

minimum

wave

speed.

IP

is

a counter

used

in

subroutine

pump'

VIit

an

arrray

containing

the

K

values

of

the

valves

in

the

network

(21

per

nul"-")'

QV

is

the

array

which

contains

nows

through

varves

and

these

are

working

variables

only.

FK

is_the

bulk

modulus

of

the

fluid.

Fr,

it

Young's

modulus

for

the

pipe

wall

material'

TK

is

r errrrent tim-e. AP is

the

first

coefficient

in

the

pump

head

tficient

and

CP

is

the

third

coefficient'

PN

PNS

is

the

steady

rotational

speed

of

the

)

pump

(note

that

in

this

particular

version

ri

variation

in

the

efficiency

with

speed

or

rs

of

the

program

include

this

facility)'

TP

is the

time

at

which

a

pump

is

tripped.

Po

is

the

no-flow

powgr

required

to drive

the

po*p

under

this

condtion-.

PINER

is

the

pump's

moment

of

inertia'

DP

is

the

pump

impeller

diameter.

FIV

is

the

head

in

metrei

of

water

at

which

the

fluid

boils

at

r^--^-^+.-a i a rha heqd .nrre.snondins to the

fluid's

vapour

pressure.

iifi:11ffi:1ffiil;i

d;'#;"^,'il

(!";il;;;

;hE

ai,

nessers

have

bien

asiumed

to

be

vertical

cylinders;

they

can

have

any

other-geometry

bu11hi1

is

left

to

the

programmer

to

d;;;iil;

nimselj).

DTF

is

the

'D'epth

in

the

'T'ank

at

the

'F'inish

of

the

time

step.

DTI

is

the.D'epth

in

the.T'ank'I'nitiaily.

pArRI

is

the

pressure

of

the

air

in

the

air

vessel

initia[y.

eolv

is

the

polytropic

index

in

the

equation

of

state.

AT

is

the

cross-sectional

area

of

the

tank.

f{i

i,

itt"

height

of

the

base

of

the

tank

with

reference

to

the

centreline

of

the

pipeline

below

it.

AC

is

the

area

of

the

choke

fitted

in

the

choke

ring

in

the

air

vessel.

AE

is

the

area

when

the

choke

ring

is

open'

ry9

it

the

time

of

starting

of

valve

movement.

TVF

is

the

time

of

finishing

of

valve

movement.

KSR

is

either

-

1. or

1

(if

it

is

-

1.

,

the

valve

is assumed

to

be

initially

clo99d

and,

if

it

is

1.

,

the

valve

is

assumed

io

be

initially

opened)

' IcHg

is

an

integer

variable

provided

to

give choice

as

to

how

output

is maie.

TSIM

is

the

time

to

be

simulated

by

ih"

*o.

DTls

the

time

step

of

the

integration'

Subroutines

247

.SUBROUTINE

INPDAT

coMHoN

/

AA/N,EL(50),O(50),

EK(50

oP(5,r ),v1

(50,2!r,v2(50,zLl,z(50'

JUNCT

(50,

5},HRES(50,

2

}'

PI,HA,HG,

FK,

FE

(50

i,

TK(50),

T,

AP(50)

lBl!5-o

)

rpi

so

),

Po(50

),

PrNER(50),

DP(50)'tl

AC(50l

,est50)

,TVS(50)

,TVF(50)

'KS

ICHO,

TSIM,

DT,

II

,

KK

nRrTE(

1,100)

FORI''AT(i

ENTRY

OF INPDAT')

l.tRITE

(

1

,59)

FORMAT('

THE

INPUT

DATA

FILE')

READ(5,1)ICHO

READ(5,1)IP

I.IRITE(

1,1)

ICHO

I4RITE

(

1,1)

IP

READ(5,1)N

t,tRITE(1,1}N

FORMAT

(

13)

READ

(

-c. 12

)

tl

tiRrTE(

1,12)Ll

G=9.

81

Sec.

12.41

246

1

a

3

4

5

6

100

59

248

The

programming

of the

wave

equations

1[ch.

12

PI

=3

. 14159

READ{5,10)nNU

T,IRITE(1,1O)t,|NU

FORMAT(F12.8)

READ(5,8)DX

I,TRITE(1,8)DX

troRMAT(Fl0.2)

READ( 5, 22)HA, HG, HV, TST}1,

POLY,

FK,

RhISP

WRITE

(

!

,22)HA,

HG, HV,

TSIM, POLY

,

FK

,

RLISP

FORHAT

(

5F 12

.

4,

2Gt5 . z',)

READ(5

,231E1,82

T.IRITE

(I

,23IEt,E2

FC'RMAT

('/Ftz.5t

DO

50

f=l.N

READ(5.2)EL{ I

) .

D(I

)

.

TK( I)

.

EFI(I)

.

FE(I

)

LIRITE

(

1

,?IEL(.I

)

,

D

(

I

)

,

TK

(

I

)

,

EK

(

I

)

,

FE

(

I

)

FOP.MAT(5F18.5i

READ(5

,:1)Z(r,

1)

,

Z(r

,2)

wF.rrE(

1,3iz{r,

1

l,z(I,2)

FORMAT(2FT2.4')

READ(5,

4)IROUTE(

I,

1

),

IROUTE(I,

2}

T,IF.ITE(1,4}IROUTE(I,

1

},

IROUTE(I,

2}

FORHAT

(2r4)

IF( IROUTE

{T,2).NE.

2

)COTO

6

RFAD{_c. Ti.TUNCT

(

I,

1

i

TJPITE(

1,

7),IUNCT

(

I,

1

)

JK=JUNCT{f,1}+1

DO

5 .I=2,

JK

READ(5,7l.TUNCT(

I

,

J)

I.IRITE

(

1,

7,

JUNCT

I

I, J

)

FORMAT(

13

)

CONTINUE

rF

(

IROUTE

(

I,

1

i

. NE.

1 .

AND.

IROUTE

(

I, 1

i

. NE.

31 .

AND.

IROLiTE

{

I, ].

)

. NE. 33

)

GOTO

11

READ

(5.

!.2

)HRE-q(

I

.

1

)

WRITEi

1, 12)HP.ES(

r, 1

)

FORI'IAT(F12.3)

IF(

IROUTE

(I,2'.HE.4.AND.

IROUTE

(T,2'.

HE.

10)GOTO

13

READ(s,12)HRES(I,2)

wRrTE(1,lz)HRES(I,2)

]F(IROUTE{I,2)

.NE.

9.AND.

IROUTE

(I,2T.NE.

1O)GOTO

14

READ(5,

15)

TVS(

I

},

TVF(

I

),KSR( I

)

ttRITE(

1,

1_s)

TVS(I

),

TVF(

I

),KSR

(

I

)

FORMAT(2FL2.4,T31

DO

16 fK=1,21

READ(s,31)VK(I,

IK)

T.JRITE(

1, 31

)VK(I,

IK)

FORMAT

(G18.

5)

CONTINUE

IF(IROUTE(I,1}.LT.5.0R.

IROUTE(I,

1

)

.GT.9)GOTO

17

READ(5, 18)

AP( I

),

BP( I

),

CP(

I

),

PNS(

I

),

PN

(

I

),

DP( I

),

PINER

(

I

),

AE

(

I

)

LTRITE

(

1,

18)AP(

I

),

BP( I

),CP(

I

),

PNS(

I

),PN(

I

),

DP(

I

),

PINER( I

},

AE

(

I

)

READ(5,

19)EFF(I

),

TP(I

),

PO(I

)

WRITE

(

1

,

19

)

EFF

(

I

)

,

TP( I

)

,

PO

(

I

)

10

Fto

t2

-7

e

it)

LL

11

13

15

31

L6

t4

Sec.

12.41

Subroutines

FORMAT

(

8F12.5}

FORMAT(3F12.3)

CONTINUE

IF(IRoUTE(I,2,.NE.11.AND.IRouTE(I,1).NE.7.AND.IRoUTE(I,1).NE.g)

1

GOTO

20

READ(5,21)TNKL(I),DTI

(I),AT(I),HB(I

)

WRITE(1,21)TNKL(.I),DTI

(I),AT{I

)'HB(I)

FORMAT

GF12.4)

CONTINUE

D0

200

I=1,N

NETNO(

I

l

=EL(

Tl

lDX+t

IF

(NETNO(

I)

- LT

- 2)NETNO(

I

)

=2

EL(

I

)=(NETNO(

I

)

-1

)

rDX

249

18

19

t7

2L

20

50

2OO

CCNTINUE

READ(5,4)II,KK

DF'f I IDIU

f\E I L,I\II

END

12.4.2

The output

subroutine.

Output

consists

of

tifles

of output

tables

and

of

the output

itself.

It is

generated on

every

pass

through

the

progran;

so

output

files

may

be

very large.

Different

applications

may

require

different sorts

of output.

For instance

it may

be

thought

dLiirable

to.have

every

velocity, total

head

and

gauge

pressure head together

with

the

distance

along

each

pipe

for

every

Ax node

and

for each

At

level. This

will be a

very large

file indeed.

To organize

such

output

into a comprehensible

table

will

require

the output

of suitable

titles

to be

printed at appropriate

points in the table.

firis is

all

possible but one

sometimes

wonders

whether

the output,

when

produced,

is of muctruse

because

there

is so

much of

it.

Alternatively,

output

can

be

made

for

the

pressure

or

velocity or

flow

history

against

time

for

different

points in the

network. Such

histones

can

be stored

in separate

files

which

can be

graph

plotted

later

when the

run

has been

completed.

There

is an

alternative

way of

generating

graphs

of

these

histories

and that

is to

plot them on

the

visual display

unit

and

then,

if

ihJuser

thinks

that they

are

useful,

they

can

be downloaded

to the

printer using

screen

downloading

software

assuming

that

the user

has access

to it.

12.4.3

The wave

speed

subroutine

WASP

This

procedure

uses

the concepts

given

before

and calculates

the

wave

speed

allowing

for the

effects

of changes

in

pressure and

their consequences

as they

cause

gas

bubble evolution

and

so change

the

effective

bulk modulus.

c

r tr tt s r rtl

r I r ll

a

t

I t

t

I

I t r r a I I tt I

tr

r r t I r t

I t t

I r s r t I t

t *

t 1t

t

tt

r

a

r t f

ll *t t I

t

I t I

C

-SUBROUTIT{E

IJASP

CALCUTATES

THE

LOCAL

WAVE SPEED.

E1 IS

THE

FRACTIONAL

C

VOLUME

OF FREE

AIR

BUBBLES

AND

E2 IS

THE

FRACTIONAL

VOLUME

OF

THE

AIR

C DISSOLVED-IN

THE

LIOUID

BOTH

AT LOCAL

ATMOSPHERIC

PRESSURE.

HA

IS

THE

C HEIGHT

OF

THE LIOUID

BAROMETER

iN

METRES

AND

HG

IS

THE GAS

RELEASE

C

HEAD.

RI,ISP IS

THE MINIMUM

I.IAVESPEED

WH]CH CAN OCCUR.

HV

IS

THE

C

VAPOUR PRESSURE

HEAD

IN

HETRES

OF LIOUID.

C

-qUGGESTED

VALUES

ARE:-

E1

=

0.001,

E2

=

O-019,

HA

=

10'3'

HV

=

0'1,

250

CHG=

c

The

programming

of

the

wave

equations

2.4, RTJSP

=

100-0- THESE

VALUES

ARE FOR I.IATER.

I t t t

r

t

t t t ltttlt *

I

tl

tt r

t

*

r r t rrtt

trt I

r

tr

r

f I t

r

t *

t t

r

r r

ri

x

r

l r

r r r

r

t

)t

SUBROUTINE

I.TASP( T, J, K.C)

coltMoN,t AA

lN,Et

(

50

),

D

(

-c0

),

EK

(

50

l,

G, H, HNU, H1

(

50,

21

),

H2

(

SCt, 2t

l,

oP(50)

,v1(50

,21) ,v2t50,21) ,

Z(50,2)

,DX.,

TROUTE(50,2)

,NETNO(50) ,'

JUNCT

(

50, 5

),

HRES

(

50, 2

),

Pr,

HA, HG, E1, E2. Rttsp, rp,

VK

(

50,

21

),

QV

(

50

),

FK, FE

(

50

),

TK

(50

),

T,AP

(

5C

),

Bp(

50

),

Cp(50

),

pN

(

50

),

pNS

(

50

),

EFF

(

50

),

TP

(

50

)

.

PO

{

50

),

PINER

(

50

),

JP

(

50

),

HV, TNKL

(

-s0

r,

DTF

(

50

),

POLY.

DTf

(

50

},

AC

(

50

),

AE

(

50

),

TVs(50

)

.

TVF

{

50), KSR

(

50

},

pArRr

(

50

),

AT

i

50

),

HB

(

5

),

TCHO,TSIM,DT,TT,KK

T.TRITE(

1,

1OO) I,

EL(T

)

FORMAT(

'

ENTRY

OF I.TASP'

,15,

F12.41

P=

(H1

(

r,

J)

-

(Z{1,1

)

+

(

3

(

r, 2

)

-Z{r,1

)

.

(

J-1

)

rD}:/EL

(

r

; ) )

r

9t

E=E1

IF

(P.

LE.

HIHG)

E=81+E2

IF{

P.

LT . HVrI.l

)

P=HVr}l

E=Erl.lrHA,/P

IF(E.cT.0.8)E=0.8

c=1 -

O/soRT(Hr

(1.0-E)

/cx

(1.0/FK+E/p+D(

r

) /

(TK(r)

tFE(r

)

) ) )

IF

(C.

LT . RI|SP)

C=RllSP

c

wRrTE(1,101

)C

101

FORMAT('

EXIT OF

HASP'

,Ft2.4I

RETURN

END

12.4.4 The interpolating and fric{ion

subroutine FRINT

\ilhen

calculating the

values

at the

base

of

a

characteristic three numbers

are

required. These are the

velocity

u1,

the total head

hland the friction value

Zfullol

Ltl

gd

where the

subscript I denotes an interpolated

value.

All three values

are needed in

the calculation of the

velocity

and head

at the

node

point

a Ar

later; so it

seems

sensible

to

use one subroutine to calculate

all three.

c

lltl ttl t t tttttltrtt lttr

ttrr t

rr

t a I t

rlr

lI S

r r r r.t

I t t lrr t

rr l r r artrt

I

r

C

SUBROUTINE FRINT

CALCULATES

INTEP.POLATED VALUES OF HEAD(TOTAL),

C VELOCITY AND Ff

{

=2IFIVIaABS{VI)'DT/D).

RE IS

CATCULATED

AND IF

C RE IS IESS TIIATI 2300, F IS ICADE

EOUAL TO 15/RE AND JF IT

IS GREATER

C THAN

2300

IT IS OBTAINED FROI'I

THg COLEBROOK-IIIHITE EOUATION

USING THE }'OODY FOR}'UIA AS

AN

INITIAL

APPROXIMATION.

c

t r

t: *

tt

rtttlrt ltttl tr rt

ta t *t trt t lttr I tl

t

I r

r

t

tr

t t I r I

t

t * t a t x t tr I

I

*

suBRouTrNE

FRrNT( r, J,Hr,Vr,

Fr, L,K,C)

COHMON

/

AA/N,EL{50

),

D

(50

),

EK

(

50

),

G, H, [.lNU, H1

{

50, 21

),

H2

(

50,

21

},

oP( 50),

vl

(50,

21

),

V2

(50,2!),2

(50,

2

),

DX, TROUTE

(

50, 2

),

NETNO( 50

),

JIINCT(-c0,5)

,HRE-q(50,2l,PI,HA,HG,E1,

E2,RI.ISP,

fP,VK(50,21)

,QV(50)

,

FK,FE(50)

,Tl{(50) ,T,AP(50},BP(5rl) ,cP(50)

,

PN(-=.C)

.

PNS(50)

,

EFF(50)

,

TP

(

50

),

PO

(50

),

PII{ER

(

-c0

},

DP

(

5C

)

.

HV, TNKL

(

50

)

.

STF

(

50

),

POLY, DTr

(

_c0

),

AC(50)

,AE(50),TVS(50)

,TVF(50)

,KSR(50)

,PAIRI

(-s0)

,AT(50) ,HB(50) ,

ICHO, TSIM, DT, TT,KK

t.rRrTE.(1,100)I

FORMAT(

'ENTRY

OF

FRIIIIT'

,

T5)

IC=0

CALL WASF(T,J,K,C)

DDX=

(C+J'V1 (f,

J)

)

rDT

JA=K-J

VI=V1

(I,

J)

-(Vl

(I,

J)-Vl

(f

,.TA)

)

IDDX,/DX

lll=Hl

(

I, J)-(H1

(f

,

J)-H1

(I,

JAI

)

1DDX,/DX

RE=ABS(VI)rD(I)/HNU

'

1cn.

rz

1

a

3

4

5

6

c

100

1

2

3

4

5

6

c

100

Sec.

12.4]

Subroutines

IF(RE-LT.0'1)RE=O'1

3

c

101

25L

IF(RE.

LT.2300

- 0

)F=16'

O/RE

F1=F

IF(RE.

tT.2300.

0

)coTo

3

F1=0.

001375r

t

r. 6iiioooo.

0rEK

(

Tl

lD

tI

)

+

1000000'

o/RE)

r t0'

3333)

F=!

.0/

(-4.0'Al,o6i07i.stt

(

2.0tsoRT(F1)

rRE)

+EK(

r

)

/D(

r

| /3

-7,l't2

rF(ABS(F1

/F-t

-0)

-LT.

0'

0001

)Goro

3

IC=fC+1

F1=F

GOTO

2

F=F1

FI=Z.0*FrvIrABS(VI

)

lDTID(

I

)

WRITE(1,101)

FORMAT('

EXIT

OF

FRINT')

RETURN

END

12.4.5

The

air

vessel

subroutine

AIRV

In

this

subroutine

the

technique

used

is

that

given in

the

preyious

relevant

chapter.

This

subroutine

can

be

called

at

the

downstreim

end

of any

pipe

!n

the

network'

If an

air

vessel

is

present

at

a

distance

r

down

any

pipe' this

procedure

can

be

used

by

introducing

an

additional

node

into

the

netw;rkit

*hich

the

air

vessel

is

located.

SUBROUTINE

AIRV(I)

coMMoN /M/N.EL(50)

,

D(50)

'

EI

1

oP(50),v1(50,2L),V2(5O'2t\,Z',

2

JUNCT(50,5),HRES(50,2),Pr,HA

3 FK,

FE

(50),TK(50),T,AF(50)'

BP

4 TP(50

),

PO(50).,

PrNER(50

),DP(51

5

AC(50),AE(50),TVS(50),TVF(50

5 ICHO,

TSII.',DT,II

,KK

c

IIRTTE(1,100)

1OO

FORI'AT('

ENTRY

OF

AIRV')

NET=NETNO(

I

)

CALL

I.IASP(

I,

NET,K,C)

CALL

FRINT{I'NET,HX,VX,FX,

1,K,

C)

CALI

FRINT(

I+1,

1,HY,vY,

FY,

-1'K'C)

AL=PI/A.OxD(I)'D(I)

AZ=P]

/4.0*D(

I+1

)

rD(

I+1

)

DH=

(A1rV1

(

I,NET)

-A2*V1 (

f+1'

1

) )'DTr/AT(

I

)

IF(T.GT.DT/2.0)GOTO

1

pAIRI

(I)=(Hl

(I,NET)-HB(I

J

-2G,2)-DTI

(I

)

rn

DTF(I)=DTI(I)

1

DTF(i)=DTF(l)+DH

HAIR=

t

tillxi

(

I

)

-DTF

(

I')

t

/

(TNKL(

I

)

--DTI

(

I

) )

)

r'PoLYTPAIRI

(

I

)

/t'l

HP=HAIR+HS1

1

)

+Z{

I, 2

)

+DTF

(

I

)

v2(

I

,NET)=VX-FN-G/Cx

(HP-HX)

V2

(

I+1,

t

)

=VY-FY+G

/Ct

(HP-HY)

Hz(I,NET)=HP

H2(I+1,1)=HP

DTI{I)=DTF(I)

c

ttRrrE(1,101)

252

The

programming

of the

wave

equations

'

[ch.

12

101

FORMAT('

EXTT FROM AIRV')

RETURN

END

12.4.6

The

upstream subroutine

LJPSTR

This

subroutine

models the unsteadybehaviourof

an

upstream reservoirinwhich

the

head is

maintained

constant. There

can be as many

reservoirs

as there are

pipes.

The

analysis which this subroutine models

is

given

in the

relevant

chapter.

1

c

J

4

5

6

SUBROUTINE

UPSTRE

(

I, K)

cotfMoN

/AA/N,Et(50)

,D(50)

,

EK(50)

,G,W,ttNU,Hl(50,21),H2(50

,2!) ,

ap(50

)

,

v1(50

,2t!.

,v2

(50

,ztl

,z

(50,

2)

,DX,

TROUTE(50

,21 ,NETNo(50

)

,

JLTNCT

(

50,

5

),

HRES

(

50,

2

),

pr,

HA,

HC, El,

E2,

RI.lSp,

rp,

VK

(

50, 21

),

OV

(

50

),

FK, FE

(50

),

TK

(

50), T, Ap

(

50

),

Bp

(

50

),

Cp( 50

),

pN

(

50

),

pNS

(

50

),

EFF

(

50

),

TP

(

50

),

PO

(

50

),

PrNER

(

50

),

Dp

(

50

),

HV,

TNKL

(50

),

DTF

(

50

),

pOLy,

DTr

(

50

),

ACt50)

,AE(50)

,TVS(50)

,TVF(50)

,KSR(50) ,pArRr

(50)

,AT(50)

,HB(50)

,

ICHO,

TSIM,

DT, rr

,

KK

wRrTE(1,100)

FOPMAT

{

'

ENTRY OF

UPSTP.E'

)

CALL I.IASP(T,2,K,C)

CALL

FRrNT( r,

1, HY,VY,

FY,

-1,K,C)

H2(I,1

)

=HRES(I,

!)

+7.1

1,

1

)

+HA

V2{

I, 1

)

=VY+G,/Cr

(H2(

I,

1

)

-HY}

-Fy

HRITE(1,101

)

FORMAT('

EXIT OF UPSTRE')

c

100

c

101

RETURN

END

12.4.1

The

downstream subroutine

DOTTNST

The

downstream

subroutine models

a

constant-head

reservoir

located

at the

down-

stream

end of a

pipe.

As with

the upstream

subroutine

there can

be

as many

downstream

reservoirs as

there

are

pipes

in

the network.

The

analytic

basis

is

given

earlier in this

text.

SUSROUTINE

DO[.'NST(

I, K

)

COI{MON

/

AA/N,EL

(

50

),

D

(

50

),

EK

(

50

),

G,

[.t,{rlNU,

H1

(

50,

211,H2(

50, 21

),

oP(50

),

v1

(

50, 21

),

V2

(50,

21

),2(50,

2

),

DX, TROUTE

(

50, 2),

NETNO(50

),

JUNCT

(

50, 5

),

HRES

(

50, 2

),

pr,

HA, HG,Et,E2, RI.lSp, rp,

VK

(

50, 21

),

OV

(

50

),

FK, FE

(50

),

TK

(50

),

T,

Ap(50

),

Bp

(50

),

Cp( 50

),

pN

(

50

),

pt{S(

50),

EFF

(

50

),

TP

(

50

),

PO

(

50

),

PrNER

(

50

),

Dp

(

50

),

HV, T!{KL

(

50

),

DTF

(

50

},

PoLy,

DTr

(

50

),

AC

(

sfr

),

AE

(50

),

TVS

(

50

),

TVF

(

50

),

KSR( 50

),

pArRr

(50

),

AT

(

50'),

HB

(

50

),

rcHo, TSIM,

DT

,

rr

,

KK

LIRITE(1,100)

FORMAT('

ENTRY OF

DOI,JNST')

NET=NETNO

(

I

)

CALL

WASP(

T,

NET-1,K,C)

CALL

.FRINT

(

I,NET,

HR,

VR,

FR,

1,K,C)

H2

(

I

,

t{ET

)

=HRES

lI

,2)

+Z(I

,2

)

+}lA

Vz(T

,NET

)

=VR-G

lcx

(Hz(I

,

NET

)

-HR

)

-FR

r{RrTE(1,101)

FORMAT('

EXIT OF

DO}TNST')

RETURN

END

1

2

3

4

5

100

c

101

c

Sec.

12.41

Subroutines

253

12.4.8

The

pump

subroutine

PLJMP

This

subroutine

is complex

in that

it solves

a number

of cases.

Pumps are

commonly

used in

conjunction

with other

devices

such as

air

vessel or

valves.

A

pump

may

be

either

a

booster

pump,

i.e.

an

in-line

PumP,

or

it

may be

an upstream

pump

such

as

a

suction-well

pump. A

suction-well

pump

draws

water from

a

well, located

upstream,

and

feeds

a network

downstream.

It may

supply

a rising sewage

main,

it may draw

from

an irrigation

well.

The

case

may be

a

potable water supply

or

it may

be an

oil

well. It may

even

be

a chemical

processing

plant, which delivers

its

product to

a

pipeline which feeds

a distant

network,

somewhat

similar

to the

circumstance

that

is

found

in Europort,

near

Rotterdam.

Itlltftttllltlarltttltrrltltll*taltltrltl

f, I

lIt

t*llIlItIt

llt:xlltll

.SUBROUTINE

PUHP

CALCULATES

THE FLOI,I

THROUGH

THE

PUMP

AND

THE

HEADS

AND

VELOCITIES

UP

AND

DCWNSTREA}I

OF

THE

PUHP.

Itr'

THE

TIME

IS

LESS

THAN

THE

PUMP

TRIP

TIME

THE

RUNNING

SPEED

I-S

KEPT

AT THE

STEADY

VALUE

BUT

IF

THE TrME

Ei(cEEDs

THE

TRIp

TIME

tlEtl

VALUES

tlF

PLIMP

REVS/MIN

ARE

CALCULATED

TO

SIMULATE

THE

PUMP

RUN

DO[']N.

IF

IROUTE

IS

GIVEN

THE

VALUE OF 31

THE

PUMP

IS

A

SUCIION

WELL

PUMP

AND

IT

USES

THE

UPSTREAM

RESERVOIR

LEVEL

AS

THE

-SUCTION

IIELL LEVEL.

IF

IROUTE

IS

GIVEN

THE

VALUE

OF 32

THE

PUHP

IS

AN

INLINE

BOOSTER

PUMP

AND

MUST

HAVE

A SUCTION

PIPE CCNNECTED

UPSTREAI''

AND

A

DELIVSRY

PIPE

DOI'INSTREAM.

IF

]ROUTE

IS

GIVEN

THE

VATUE OF

33 THE

PUMP

IS

A SUCTION

I'IELL

PI.'HP

EOUIPPED

WITH

AN

AIR

VESSEL CONNECTED

I}'MEDIATELY

DOI.INSTREAT'!.

IF IROUTE

IS

GIVEN

THE

VALUE

OF

34

THE

PUMP

IS

AN

INLINE

BOOSTER

PIJMP

EGUIPPED

I'IITH

AN

AIR

VESSEL

CONNECTED

IMMEDIATELY

DOI.INSTREAM-

PUMP IS AN

UPSTREAM

PROCEDURE

SO IROUTE(I,I)

MUST

BE

GIVEN

ONE

VALUE

FROT.' THE

LIST

31

,32,33,34

r llt ttrt

tlrsx

l(l tttr

I

r rr I

I

tl

I t rr

t I t

r I tr

r I

rr l. I t

t ltl I tt

rrrr

r ! t i t t

r r t

AC

(50

),

AE

(

50

),

TVS(

50

),

TlrF

(50

),

KSR

(

50

),

PArRr

(

50

),

AT

(

50

),

HB

(

50

)'

rcHo,TsrM,DT,Ir,KK

tfRrTE(1,100)

FORT{AT('

ENTRY

OF

PT'MP')

IF(IROUTE(I,

1

)

.8O.33.OR.

IROUTE(I,1)

-E4.34)GOTo

10

IF(IROUTE(I,1 }

.8Q.32)

GCTO

1

HSU=Z(

J, 1

)

+HA+HRES(

I,

1

)

CALL

I.IASP(I,1,K,C2)

CALL

FRrNT(r,

1,HY,VY,

FY,

-1,K,C2)

APZ=PT/4tD(I)'D(I)

AP1=1.0

FX=0.0

VX=0. 0

HX=O.0

IF(IROUTE(I,

1

)

. EO.

31

)GOTO

2

NET=NETNO(

I-1

)

CALL

I.IASP(T-1

,

NET,

K,

Ci

}

CALL FRINT(I-1,NET,HX,VX,FX,

1,K,C1

)

API=PI/4xD(

I-1

)

rD(

I-1

)

AL=CP

(

I

)

1

a

&

3

4

5

6

c

100

The

programming

of the wave

equations

[Ch.

12

BET=

(C2/

AP2+CL/AP1

)

/c-BP(

I

)

*pN(

I

)

GAM=HY-HX-AP(I

)'PN(

I

)

rpN(

T)

+CZ/Gt

(Fy-Vy)

+C!/Gt

(

FX-VX)

SURD=BETTBET-4

. 0

TALIGAM

IF(

SURD.

LT.

0. 0) SURD=O.

0

OP

(

I

)

=

(

-BET+SQRI

(

SURD)

|

/

(Z'

AL,

IF(AP(I

)

.

LT. 0.

0)AP(

I

)=0.

0

V2(I,1)=AP(I)/APz

rF(

rRouTE(r,

1

)

.

EA. 31

)GOTO

3

v2

lI-1,

NET)

=QP

(

I

) /AP1

H2

(

f

,

7

)

=H'I+CZ/GI

(V2(

I,

1

)

-Vy+Fy)

H2

(

I-1, NET

)

=HX-Cl/G'

(V2(I-1,NET)-VX+FX)

IF(IROUTE(I,

1

)

.EO.32)GOTO

4

HzlI

,

Ll

=HY+CZIGI

(V2 (

I. 1

)

-VY+FY)

IF(T.tT.TP(I)

)GOTO

6

IF

(

IROUTE(

I, 1

)

. EO.

31

iHU=HSU

IF( IRCUTE(

I, 1

)

. E0.

32)HU=H1

(

I-1, NET)

DH=HI

(

I,1

)-HU

IF(DH.LE.O.O)GOTO

7

Pl{Rl=-tlr0P

(I

)

rDH,/EfF{

I}

PIIR2=-PO(

I

)

r

(PN(I)

/PNS(

I

) )

r r3.

0

PtlR=PIJR1

IF

(

PWR2

. LT. P[,1R1

)

PtlR=PlIR2

IF(DH.GT.O.O)GOTO

5

IF(PN(I)

.LE.O.O)GOTO

6

CV=Z.0-2-

0rct(60.0/{PITDP(I

) )

)

rtzrAP(I)

TER=50.0rctBP(I

) /(

(CV-l.0)

'PITDP(I)

)

EN=-DH-CP{r)

roP(r)

rGP(

l)-cv

/

(2.0rc)

r

( (PFDP(r)

tpN(

r)

/oo.0

)

t t2-

2. 0rpr

rDp(

r

)

*pN(

I

)

rQp(

I)

/60.0rTER)

PI'fR=tlrQP(

I)

*EN-PO(I)

r

(PN(I

) /PNS(f

) )

tr3

PN(

I

)

=PN

(

I

)

+3600.

0

TPHRIDT,/

(

4

. 0

tPI rPI

tPN

(

I

)

TPINER

(

I

) )

IF

(PN(I

)

.

LT. 0. 0)PN(

I)

=0.

0

CONTINUE

IF(

IROUTE(I,

1) .80.31.OR.

IROUTE(I,1)

.EO.32)GOTO

9

rF(T- LT

.DT

/2-0)PArRr(r

)=(Hl

(r,

I

)-HB(r

l-z$,

1

)-DTr

(r

) )

rfl

IF

(

T.

LT .DT

/2.

0

)DTF(

I)

=DTI

(

I

)

ACR=AE(I)

AP7=PI/4.0rD(I)rD(I)

OT=OP(I)-APltvl(f,t)

IF

(

OT-

LT.

0. 0

IACR=AC(

I

)

rF(

rRouTE(r,

1

)

-EO.

34)COTO

I

HSU=Z(

f

,

I

)+HA+HRES( I, 1

)

CALL

FRINT(

T,

1,HY,VY,

FY,

-1,K,C2)

IF(T. GT.

TP(

I

)

)PN(I)

=0.

0

IF(T.GT.

TP(I

)

)OP(

r

)=0.

0

IF(T.GT.TP(I)

)GOTO

15

AL=CP(

I

)

BET=-(BP(I)rPil(I))

GAH=HI

(

I, 1

)-AP(I)

tPN(

I

)

tPN(I

)-HSU

OP(

I

)

=(

-BET+SQRT(BETTBET-4.

0rALrcAM)

)

/

(2.

O'

AL)

IF(OP(

I

)

.

LT.

0. 0)0P(I

)

=0.

0

DTF(I

)=DTF(I

)

+

(OP(I

)-APlrV1

(

I,

1

)

IDT,/AT(I

)

PArR=PArRr

(r)

t

( (TNKL(I

)-DTr

(

r

) )/(TNKL(r)-DTF(

I

) ) )

rrpoly

VT=OT,/ACR

H2(I

,1

)

=PAIR,/91+DTF(

1)

+HB(

11+Z(f

,

1)

+VTTABS(VT

|

/

(2.Ol,c,)

Vz(I

,1

)

=VY+G/CLI

(H2(

I

,1)

-Ht')

-Fy

IF( IROUTE(I,

1

)

.

EO. 33)GOTO

9

Sec.

12.41

Subroutines

255

NET=NETNO(

1-1

)

CALL

FRINT

(

I-1

,

NET,

HX,

VX, FX,

1

,

K,

C1

)

CALL

FRrNT

(

I

,

1

,

HY,

VY,

FY,

-1

,

K, C2

)

AL=PT/

4.0

rD(

I-

1

)

rD

(

I-1

)

A2=PI/4.0'D(I)

rD(I)

IF

(T

-GT

- TP(

I

) )oP(

I

)

=0

'

0

IF(T.GT.

TP(

I

)

)PN(I

)

=0-

0

IF(T.GT.TP(I)

)GOTO

17

AL=CP(

I

)

BET=

(C1l

(cxA1

)

-BP(

I

)

rPN(

I

) )

GAM=HI

(

I,

1

)

-HX-CIrVX

/G+C|IFXIG-AP(I

)

*PN(I

)

rPN(I)

SURD=BET

rBET-4

.

0tALTGAM

IF

(SURD.

LT.

0.

0

)SURD=0

-

0

OP

(

I

)

= (

-BET+SQRT(SURD),

/ Q.CIAL)

IF(OP(I

)

. LT-

0

- 0)OP(

I)=0-0

DTF{I

)=DTF(I}+

(OP(I)-A3'V1

{I,

1

i )

{DT/AT(

I

)

PAIR=PAIRI

(

I

}'

(

{TNI(L(

I)-DTI

(I)

)

/(TNKL(I

)-DTF{I

i

} }'I'POLY

VT=

(OP(

I

)

-A2tV1(I,

1

) )/ACR

H2(

I, 1

)

=PAIR,/II+DTF(I

)+HB(

11+Zl

I,

1

)+VTaABS(VT)

/

{2'O*GI

V2(

I, il

=VY+G/CZt

{.H2(I,

1)

HY)-FY

H2

(

I-1,

NET)

=HX-CI/Gr

(V2(

I-1,NET)

-VX)

-CllGrFX

V2

(

I-1,

NET

)

=YX-G/CLr

(H2(I-1,NET)-HX)-FX

t7

6

10

IF

(T.

GT'

TP(

I

) )PN(I

)=0.

0

9

CCNTINUE

IF

(

H2

(

I-1,

NET

)

-z

t

I

-1,2|

.LT.

Hv

)

H2

{

r

-

1,

NET

)

=HV+Z

(

r-1,

?

)

IF

(H2

(

I,

1

)

-Z

(

I,

1

)

.

LT.

HV)H2

i

I, 1

)

=HV+Z(

I,

1

i

c

LIRITE(1,101)

101

FORMAT('

EXIT

OF PIJI.IP.)

RETURN

END

12.4.9

The

valve

subroutine

VALVE

cr.trrrraa'rrlltrtaraaaaaasacgr:l!rrErlt**tlttrlltlr'lltlttrrt|',||a

C

SUBROUTINE

VALVE

CALCI'LATES

HEADS

AND

VELOCITIES

UPSTREAT'I

AND

DOI'IN

C

STREAM

OF

A

VALVE.

KSR

CAN

BE

SET

TO

1

OR

-1'

IF

KSR

IS

SET

TO

1

cTHEvALvEoPENsBETI.IEEI|THES.TARTTIMETvSANDTHEFINISHTIMETvF

C

AND

IF

IT

IS

SET

TO

-1

IT

CLOSES

BETI'IEEN

TI{ESE

TIMES'

THE

VALVE

K

C

VALUE

:-

VALK

IS

OBTAINED

FROM

ARRI

C

TNOU

THE

OPEN

VALVE

K TO

THE

CLOSEI

C

IF

IROUTE

IS

GIVEN

THE

VALUE

OF

41

C IROUTE

IS

G]VEN

THE

VALUE

OF

42 THl

C PIPELINE

DISCHARGING

II{TO

A

RESERV(

C STREAM

PROCEDURE

SO

THE

ASSIGNMENT

C

IF

IT

IS

WANTED

TO

MODEL

MORE

COMPLEX

VALVE

MANOEVRES'

I'E'

SERVO-

C CONTROL

OR

P.S.VS

OR

P.R.VS,

THE

SUBROUTINE

MUST

BE

HODIFIED'

coFTEN0UITEcoMPLExMoTIoNscANBEMoDELLEDBYCoMPRESSINGoREXPANDING

cPoRTIoNSoFTHEvALvEARRAY,I.E.MULTI-SPEEDACTUAT0RS.

clltlllxlta'l.ttatlttll'rrlr'rrtttltlratrltllltlrar'tlttlrltlIllll

SUBROUTINE

VALVE(I,K)

cor{MoN 7;a7n'

ii

(

s0

)

:

D

(

5c

),

EK

(

50

)

r

G'

ll'

t'lNu'

Hl

(

-q0'

21

)'

H2

(

s0'

21

)'

lOP(50),v1(50,2L\,\2(50,21i,2ts0,2\,DX'TROUTE(50',2)',NETNo(50)'

2

JUNC.T(-so,ir,HRESi50,2),pr,ne,Hc,rr,E2'Rl'lSP',

rP',vK

(5o',2l)

',QV(50)

'

3

FK,

FE

(

-c;

i,

iriio

r,

ep

(

so

),

epi

so

i,

cp

(so

)'

PN

(

s0

)'

PNS(

50

)'

EFF

(

50

)'

Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

Подождите немного. Документ загружается.