Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

Sec.

6.21

Valves

t37

136

Boundary

conditions continued

lch.

6

This

is not

perfectly

accurate

but

it closely

approximates the

accurate

analysis of

the valve.

This

is

given

in the author's book Hydraulic analysis of unsteady

flow

in

pipe

networ,ts. Generally,

analysts do not even correct

the manufacturer's

graph;

so

the results obtained

from an analysis, using this correction, should be significantly

more accurate.

The effect

is not

negligible.

In

a

valve

opening, s increases from

zero

to the

value at

which

the

opening

is to be

steady,

i.e.

unity if the

valve

is to be full open

-

and this

movement must

occur in the

time specified

for

it.

Conversely,

with a valve closure, s runs from unity or whatever

partial

opening exists at the

beginning of the stroke down to zero.It is simple either

to increment

or to decrement the

value

of

s

progressively

but there are many other

different sorts

of

valve which

perform

different functions for which this simple

technique

would not be appropriate.

Examples of such valves are,

for

example,

the

pressure-reducing

valve which operates in such a

way

as to reduce the

pressure

downstream

of itself

to a

preset

value,

the

pressure-sustaining

valve which maintains

the

pressure

upstream

of itself above a

preset

value, valves which close or open

according

to the magnitude

of the

pressure,

the temperature of the flow,

or the flow

itself at some

other

point

in the

network communicated

to the valve's controls

using

some

form of

telemetry.

Far

more complicated types of control

are used

in

various

systems

in

which valves

are used

to control some

particrrlar

variable

such as the depth in

a tank or the

pressure

in a

pressure

vessel. A simple linear response to the difference

between a

control

variable and set

value may be used, but in others the s

value

is controlled

by

the magnitude

of the

time integral of this deficit.

In

all these cases,

the analysis can

be

carried

out

by

specifying

the

way

in which s

varies

with whatever

variable

controls

it,

and then,

by reference

to the array for

K, the

appropriate

value for K can

be

determined.

Once

the

value of K has

been found, the calculation

of

the heads and

velocities on

each side

of

the

valve

must

be undertaken. The

pipe

is first divided into two sections

at the

valve. The upstream

section

willcontain

a

Ax length

immediately

upstream of

the

valve

and

the downstream section

will contain a Ax length downstream of

the

valve. In the upstream

Ax length a

positive

characteristic will be

present

and,

similarly,

in the

downstream section a

negative characteristic will also be

present.

These two

characteristics,

together

with

the equation for the head

loss across the

valve, and the

continuity equation,

will

provide

a

solution of

all unknown

values.

At

point

Nthere

must

be an upstream Nand a downstream N, i.e. Nt and N2, as

there

are

two

values of head and two

values of

velocity

at a

valve

and

at time f * Ar the

apices

of

the two

triangles

must

be designated by Prand Prtorcpresent the two sides

of the

valve at this time

(Fig.

6.4).

The

two characteristic equations

are

,

hr,:

hs

*Or

@o-

u5

* F5)

therefore

h",

hp2:

h^-

hr-?

,",-%r

,r,*

?

,^

*

?

',

-|

n"-

f

r"

but

h",

hP2=#

and

uPr.

urr?

where

a,

is

the

cross-sectional

area of

the

upstream

downstream

of

the the

valve- So

*

rl*,

valve

Fig. 6.4.

c-,

*

(h",-

h*) +Dp,

-

DR * Fp

:

o

,

c

-:

- E

(hr,-

hr)

+

Dpz-rrs + lt

:

o

her

h^-%

(u",

-

u^

*

F^)

pipe

ry:v-(?.or',)',,

and

a2

is that

of

the

PiPe

138

where

Boundary

conditions

continued

lch.6

f:hn-lrs*ftr**?r"

Therefore

uu!,+

Fu",

*

y:0

-f;

r"-f

""

where

o:

(K/2g)

and

U:

(rr,.??)

The variable

up, can have

positive

or negative

values

according to the head difference

across the

valve.

This

means

that the value

u!, must

also change sign

with

the

value

of

necessary

to

repeat the calculation using the latest value

of u", that has been found. It

is unlikely

that

much error

will be introduced

by this

proceduie

as the velocity will

be

very

close tozero

anyhow; so

the

quadratic

term will be very

small.

In Fortran,

if this

is the language

being used, there is no function

for sign. It must be created by the

user. The

obvious

way to do

this

is to use

the little algorithm

sign equals

u/abs(u)

but

this is dangerous

because the time

when

sign really

makes a difference is when u is

very

close to zero. Atzero this algorithm will

fail in overflow;

so

it is necessary

to set

sign to

*

1 unless u is negative and so to avoid

the

problem.

6.3 TIIE

CALCI.JLATION OF

VARIABLES

AFFECTING THE

LIQT,ND BEING

TRANSPC'RTED

ALONG

TIIE PIPELII\IE

Two variables

that occur in the characteristic

equations are

very

often

treated as

constants.

These are the

Darcy

f

and the wave

speed

c. Both, in

fact,

are

highly

variable

and should be treated as such

in these

equations.

6.3.1

The

Darcy

f

This

occurs in

lhe

characteristic equations in the term zfululLtld. Again, remember

that in

the American

version

of this

term

the commonly

used

value

of/is

four

times

larger

than the British version;

so

the term is written

in the

USA

as

fulullM.

Below

a Reynolds

number Re of

2300

the

value

of/is

given

by 1.6lRe.

This

omits

consideration

of

the transition zone

between

Reynolds

numbers of 2C/JIG2800

but

this is

a

very

small

range and can be omitted. Assume

laminar flow

extends

up to a

Reynolds

number

of.2300 and

that turbulent flow

starts at this

value.

Although it is

most

unlikely

that

laminar

steady

flow will

occur in any

cornmercial

pipeline

it may

happen

that

during some

phases

of a

transient

the Reynolds number

may fall below

Sec.

6.3]

The

calculation

of

variables

affecting

the

liquid being

transported

139

conditions

that

then

exist

in the

pipeline,

it is

the

best

approximation

available

and it

is necessary

to supply

a

value

of

/for

the

Reynolds

numbers

below

2300

so

as

to be

able

to.oniin,r"

the ialculation

through

the

period

of time

that

quasi-laminar

flow

is

occurring.

When

calculating

the

Reynolds

number,

the

absolute

value of

the

velocity

must

be

used

and

not

the

veiocity

itself

as/and

Reynolds

number

do

not

carry

a

sign.

An

excellent

equation

that

describes

the/value

is the

Moody

formula

which

is

accurate

to

within

-5o/o

for

the

entire

range

of

the

Reynolds

numbers

that

occur

in

turbulent

flow,

i.e.

from

2300

upwards:

/=

0-001375

This

result

still

suffers

from

the

defect

that in

some

parts

of

the

Reynolds

number

range

there

is

a 5%

error.

To

eliminate

this

the

result obtained

from

the

Moody

formula

must

be

improved

and

this

can

be

done

by

using

the

Colebrook-White

formula

1 ..

{z.st

d\

rt:

-4

logls

\m*uo)

The

problem

arises

of

how

this

equation

should

be solved.

The equation

is

implicit,

so

the

value

of

/obtained

from

the

Moody

formula

can

be substituted

into

the righihand

side

of

thl

equation

and

a new

value

forf

obtained

frorn

the

left-hand

side.

This

value

can

then

beiubstituted

into

the

right-hand

side

and

the

value of/can

again

be evaluated

from

the

left-hand

side.

This

process

can

be

repeated

until

two

successivevalues

of/are

insignificantly

different.

Obviously,

this

process is

best

done

on

a computer.

Thsnumber-of

iterations

required

to

give a

highly

accurate

answer

is

four

or

five.

[t

-

(r*

to*roooooo/R,)"']

140

Boundary

conditions

continued

lch.

6

Let

the fractional bubble

content

at

the reference pressure

be

e

and the volume

of

the liquid

plus

the

gas

in the

bubbles

be V. The volume

of the

liquid will

be

(1

-

e)V

and the

volume

of the

gas

eV. Let

the reference pressure

be

p

and

let this

pressure

increase

by an amount

Ap. Assuming

that the

compression process

is isothermal,

then the

gas

volume will

become pl(p

+

L,p)eV

and the liquid volume

will

become

(1

-

e)(1

-

LplK)).V The

total

volume

becomes

(1-e)(1-(LplK)V

+

pl(p

+

Ap)eV.

Now, if. A,p is

small in comparison

withp

then

P

-

1

-r-LP

p+Lp

l+Lplp

p

so V becomes

(1-e)V(1

-

LplK)

+

(L-A,plp)eV.

The change

in

volume

thus becomes

l4l/K(l

-

s) +

elp)

Lp neglecting

second-order

small

quantities.

The

effective bulk modulus

thus

changes

according to the relationship

1

1-e

€

I

tt- K

-p'

Allowing for distensibility

effects

Usually K is so large and

e so small that

(1

-

e)lK can be

approximated

to l/K so

The density

of the liquid becomes

p(1

-

e). So

a-

L_

Therefore

Sec.

6.31

The calculation

of

variables

affecting

the

liquid

being

transported

(1

-

e)p

The

remaining

problem

now

is

to obtain

a realistic

value for

e.

At

atmospheric

pressure

there

wiilbe

a free

bubble

content

of eo.

When

the

pressure

changes,

this

bubble content

will

change.

There

will be

an increase

in

volume

of

the

bubbles

present

accompanying

the

pressure drop

which will

be

governed by

the

universal

gas

iaw. This

volume

chinge

can

be

very large

if the

drop

in

pressure is

large.

If the

pressure

drops

sufficiently,

more

bubbles

may

come

from

the

gas that

is

present in

iolution

in

the

liquid.

Evidence

is

growing that,

for

gas to come

out

of solution

sufficiently

rapidly,

on

the

time

scale

of

a

pressure transient,

to

produce

significant

contributions

to

the

bubble

content,

it is

necessary

for

the

pressure to

drop

below

a

certain

specified

value

-

the

gas release

head.

Reseirch

in

the

author's

laboratory

has

clearly

demonstrated

that

if

a liquid

originally

exposed

to,

say,

atmospheric

pressure for long

periods is exposed

to

a

low

sub--atmosphiric

pressure,

progressively

and

smoothly

applied,

gas

bubbles

will

evolve.

The

curve

of

the

fractional

volume of

gas

evolved

in the

time

/ is

plotted in

Fig.

6.5.

This sort

of

result

has

been

obtained

by

many

workers

in the

past

and is

well

fractional

volume

of

gas

Fig.6.5.

known.

The

names

of some

of

the

major

workers

in

the

field

are Epstein

and

Plesset,

a Jesuit

priest

Father

Fox

(not

the

author),

Schweizer

and

Harvey.

The

author's

ph.D.

stident,

Richard

Chilton,

was

able

to extend

this

work, filling

in

gaps in the

work

of

the

afore-mentioned

workers.

The

mode

of application

of

the

pressure

drop

makes

a considerable

difference

to the

result,

however

(Figs.

6.6

and

6.7).

Another

ph.D.

student,

Patricia

Dawson,

has

obtained

clear

and

certain

evidence

that,

if

a

pressure drop

is

applied

suddenly,

so

that

there

is

an

initial

downswing

of

pressure

to

i

level

consideraUty

U"to*

that of

the

final

pressure,

gas

release

may

occur.

Without

this

initial

downswing

no

gas release

occurs

in the

time

scale

of

pressure

transient

=--

phenomena.

It sr.rni

thai

the

initial

downswing

must

take

the

pressure

below

a

"-

r4l

(t".;.+")

1 1-e e D

-:-J--r-

K'

K'p TE

11eD

-:-+-+-

K'

K,

P'

TE

trme

K'

(1

-

e)p

742

pressu

re

0

trme

Fig. 6.6

-

Graph

of

pressure against

time for

a relatively

slow

pressure drop,

which

gives

negligible

gas

release

in the available

time.

Sec.

6.31

The

calculation

of

variables

affecting

the

liquid

being

transported

L43

6.3.3

Micronuclei

and

microcracks

Micronuclei

(Fig. 6.8)

have

been

mentioned

above

and

their

role

in

generating

Fig.

6.8

-

The

micronucleus

and

its

adsorbed

gas'

bubbles

within

the

flow

remains

to be

described.

If

the

simple

dynamics

of

a small

bubble

is

considered,

it

is easy

to

see

that

@

+

tp)ndz

-Pnd'

* ttdr

44

where

p +

Ap

is

the

pressure

within-

the

bubble,

p

is

the

external

pressure

and

t

is

the

coefficient

of

surface

tension

and

therefore

Boundary

conditions

continued

[ch.6

^p=+

pressu

re

Fig. 6.7

-

Graph

of

pressure against

time

for

a rapid

pressure drop to below

the

gas release

head,

which triggers

a much

larger continued

gas

release.

specific

value

if

gas is to

be

released

in a

time comparable

with that

in

which

we are

interested.

This

specific

value is

called

the

gas release head.This

is

explained

below.

To

grow a bu-bble

from

the nuclei

moving

within the

fluid

or

from

small

cracks

upon the

surface

of

the

vessel

which

contain

small

amounts

of

air,

a

pressure

difference

across

the

bubble

surface

must

exist.

where

R is

the

radius

of

the

bubble'

Imag

bubbles

present

and

which

is

subjected

tc

would

have

to start

its

existence

atzetorar

be

infinite.

This

would

cause

any

contain

ro

radius.

However,

if

it

may

be

assumed

ce

of

micronuclei

or

in

small

microcracks

this

problem

does

not

arise'

Adsorbed

gas

into

a

spherical

bubble

if

the

pressure

is

be

created

with

a

finite

radius

of

the

same

rnucleus.

Such

nuclei

can

be

found

in

most

neter

of

about

44

p'm some

people

think

l!1.",",

can

be

created

from

adsorbed

gas

on

a

nucleus

if

the

pressure

is

reduced

to

a

value

of

approximately

?'!

^

of

water

absolute

and,

once

the

nucleus

has

been

so

'potentiated;,

gas can-flow

into

the

bubble

from

the

main

uoav

of

the

fluid.

This

leads

to

the

idea

of

the

gas

release

head

mentioned

PreviouslY.

Microcract,

6ig.

6.9)

on

the

surface

of

the

containing

vessel

canoperate

in

the

Same

manner

as

nuclei,

as

any

carbonated

drink

demonstrates'

The

reader

is

reminded

of

how

lines

of

bubbles

rise

from

specific

sites

on

the

side

of

a

glass

after

the

first

rush

of

bubbles

(from ordinary

nuclei)

have

been

released'

These

specific

sites

are

microcracks.

trme

144 Boundary

conditions

continued

lch.6

Fig.

6.9

-

The microcrack

and its

contained

gas.

The author, in his

analysis

of unsteady

flow

in

pipe

networl<s has advanced a simple

theory

of how the value

of

e

could be

calculated

and,

whilst he

appreciates its defects,

he is

still

persuaded

that

this method

has much

to

recommend

it.

For a

pressurep

which

is

above the

gas

release pressure

head, the value

of e6 has

to

be adjusted to give the

expanded

or

compressed value

e

depending

upon the

magnitude

of the local pressure,

i.e.

e:

tsplp

uwhere

eo is the

fractional free

bubble

content in the

liquid at atmospheric pressure

pa.

For

a

pressure

p

which

is below the gas

release pressure

head the

fractional

free

bubble

content has

to be adjusted

according

to the

magnitude

of

the

pressure

relative

to atmospheric pressure

as

above, but,

additionally,

the

fractional volume

e, of the

dissolved

gas

content is assumed

to

come

out of solution

to be

expanded

or

compressed

in the

same

way

as

was

the

fractional

free

bubble content.

So

_

(eo

*

er)p

q--

.

P"

There

can be no doubt that

this assumption

is not completely

satisfactory but,

by

using

this approach,

very good

results have

been

obtained, which

have

been

verified

later by measurement

on site

when

the

scheme

analysed was

constructed.

Karplus in the 1930s

produced

graphs

of wave

speed

against the fractional volume

and

graphs

which

illustrate the type

of result

that

he obtained

are

given

in

Fig. 6.10. It

will

be seen that Karplus's

graph

does

not fit

the wave

speed

equation

given

above.

The reason

is, of course, that the assumption

on which

the

equation

is based is

that e

is

small

which

is

only

true for the left-hand

portion

of the

diagram.

At

e

:

0 the wave

speed is 1460 m/s as

one

would

expect

and at

e

:

1 it

is 340 m/s which

is the

speed

of a

sound wave

in air. For

values

of

e

in

between,

it will

be

seen that there

is a

great

reduction

in

wave

speed; so for

very

small values

of

e

the

reduction

is large. For

most

values

of

e

it would

be reasonable to

assume

that the wave

speed is that

of

the

nearly

horizontal

portion

of the

graph

except for

the two

extreme values

of

e,

i.e.

0

and L.

The value

of

e that occurs during

a

pressure

excursion is

unlikely

ever to rise as high

as

unity;

so

a sensible

way

of using

this

diagram

is

to take off the wave

speed

Sec.

6.3]

The calculation

of

variables

affecting

the

liquid being

transported

1460

m/s

I

Wavespeed

340 m/s

Minimum wave

soeed

Fig. 6.10

-

Wave

speed against fractional

volume

of

gas.

corresponding

to the horizontal

portion

of the

graph

which

will

be called minwasp

(minimum

wave speed) and

to use the equation to calculate the

value

of the

wave

speed. If

it

is

less than minwasp,

use minwasp;

otherwise

use the calculated value.

145

Sec.

7.21

The

continuity

equation

r47

where b.

is

the

surface

width

of

the

channel.

This

equation

states

that

the

rate

of

change

in

flow

over

a unit

length

of

the channel

is equal

to the

rate of

change

in

storalge

of

the

flow

within

a

unit

length

of

the

channel.

Alternatively,

this can

be

stateJ

as

the

flow

that

enters

the

Ar

length

either

leaves

it at

its

downstream

end

or

is

stored

within

the

length

by an

increase

in

the depth.

The

negative

sign

is

introduced

to

take care

of

the

fact

that

an

excess

of

inflow

(a

negative

value of 0(av)/0x)

must

equal

the

rate

at

which the

volume

of storage

is made

available

by the

rise in

the

surface

level

over

the

length

of

the

Ar.

As this

is

positive,

a negative sign

must

be

introduced

to

make

the equality

possible.

Differentiating,

Unsteady

flow

in open channels

7.I

INTRODUCTION

In

open channels,

unsteady

flow

is much more common

than

steady

flow.

Rivers are

constantly rising or

falling, either

in a

state

of flood or on

the recession

curves of their

hydrographs. Man-made

channels

can approximate

to stOady state

but even they

spend much

of their

time in

unsteady

state.

Unlike

most

pipes, channels are

not

only

of circular cross-section.

They may of

course

be of circular

cross-section,

e.g. sewers,

but more commonly

they are

rectangular or trapezoidal;

so

the techniques used

to analyse them must

be indepen-

dent

of

shape.

The equations

that

govern

unsteady

flow in open channels

are

very

similar indeed

to those of

pipe

flow but they

differ in one

respect.

The

cross-section

of

the

flow

,is

not bounded

as it is in the case of

pipes,

as the free surface,

which

constittites one

boundary,

is

positioned

according to the

dynamics

of

the

problem.

As in

pipe

flow

these equations

turn out to

be

quasi-linear

hyperbolic

partial

differential

equations.

The

development of these equations

can be

performed

as in

Fig.7.1.

(Aul

Fig.

7.1

-

Profile of Ar

length of free surface flow.

7.2

THE CONTINUITY

EQUATION

The

continuity

equation

for

an unsteady free surface

flow

is

0(.4u):

0x

ff,**n*u"#:o

*a%y#*r,

ff=o

but

Dividing

through

by

A,

but

Alb,:

6

which

is

the

mean

depth

based

on the

surface

breadth. so

-ad

uD"

6*

ad

u-*0

dx

ub,Od

*aud

abs+99*4

!:O

AOx'A

dx'Ox

A)t

0u

Ad

quddb"

#*a+

o

du:o

cross-sectlon

a

+Eg

148

Non

prismoidol

rectongle

-lrke

chonnel

Ea=BEa+aEa

Fig.7.2.

but c

:

V(g6)

where c is the celerity

of a small

wave on the surface of stationary

fluid.

Therefore

Sec.

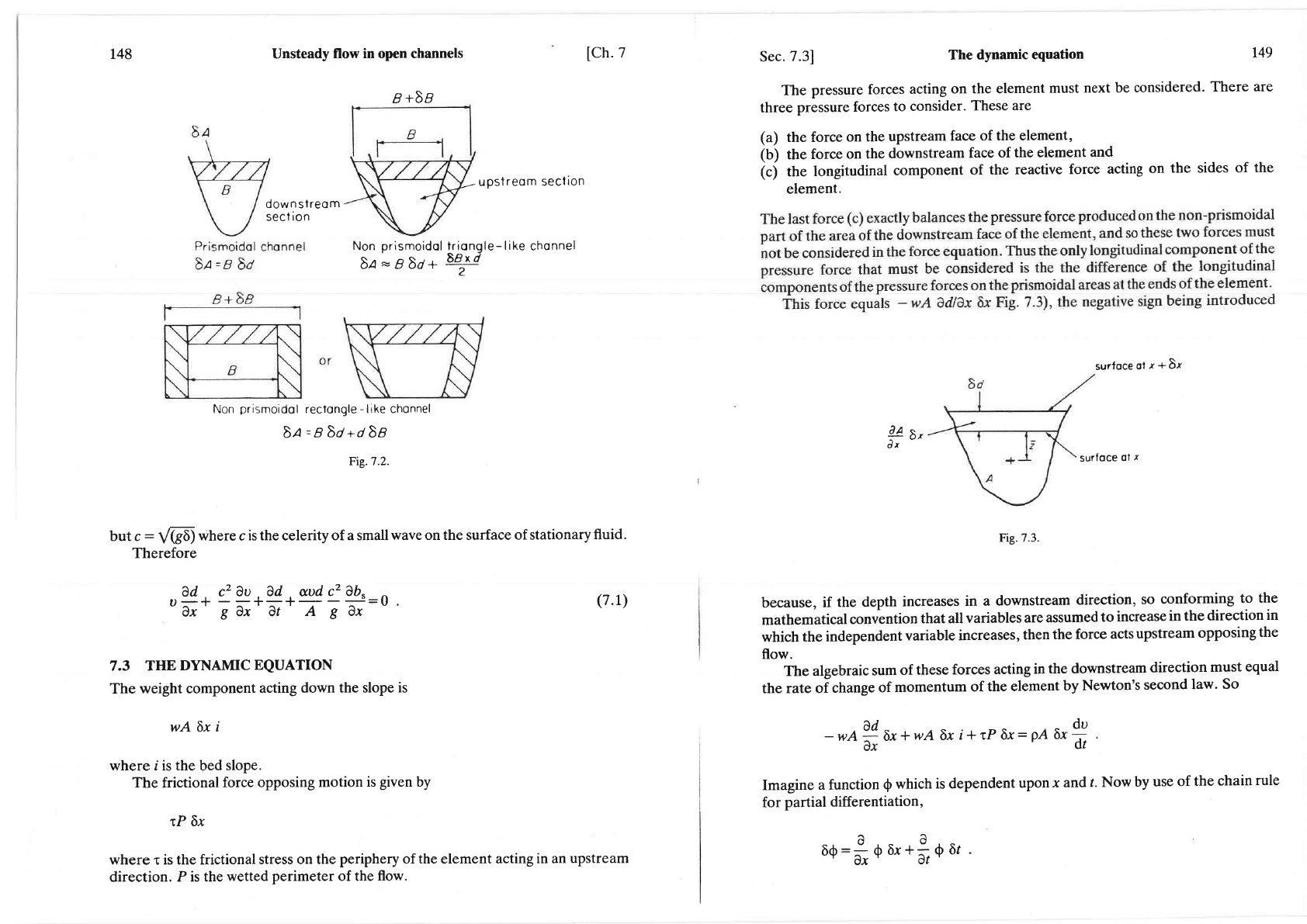
7.31

The dynamic

equation

t49

The

pressure

forces

acting

on

the element

must

next be

considered.

There are

three

pressure

forces

to

consider-

These

are

(a)

the force

on

the

upstream

face

of the element,

(b)

the

force

on

the

downstream

face

of the

element

and

(c)

the

longitudinal

component

of

the

reactive

force

acting

on

the sides

of

the

element.

surfoceotr+Er

surfoce

ol

r

Fig.7.3.

because,

if

the depth

increases

in

a downstream

direction,

so

conforming

to the

mathematical

convintion

that atl

variables

are

assumed

to

increase

in

the

direction

in

which

the

independent

variable

increases,

then

the force

acts

upstream

opposing

the

flow.

The algebraic

sum

of

these forces

acting

in

the downstream

direction

must

equal

the

rate of

change

of

momentum

of

the element

by

Newton's

second

law.

So

-wA

6x*wA6xi*rp6x:pA6r

du

dt

Imagine

a function

S

which

is dependent

upon

x and

r. Now

by

use

of

the

chain

rule

for

partial

differentiation,

Unsteady

flow in open channels

downstreom

secl

ion

upstreom

section

lch.

7

Non

prismoidql

triongle-

| ike

chonnel

6a'* BSd+

ff

!t,

dx

Ad

c2 0u Ad

q,ud

cz 0b"

'ar*;ar*ar*

AE ar:u

(7.1)

7.3 THE

DYNAMIC

EQUATION

The

weight component

acting down

the slope is

wAExi

where

i is the bed slope.

The

frictional

force opposing

motion

is

given

by

rP 6x

where

r

is the frictional

stress on the

periphery

of

the

element

acting

in an

upstream

direction.

P is the

wetted

perimeter

of the

flow.

ad

0x

DO:*

O

D'**

06r

Sec.7.4l

The

characteristic

forms

151

150

Unsteady

flow

in open

channels

lch.

7

(7.2)

(7.1)

(7.2)

Dividing

through

by

6r,

60:40

6x*00

6r

ax

&'r

dt

'

Replacing

S

by

u, and

as 6l/6r,

when

taken to

the limit,

is

u,

then

du

0u

A:

ar

'*

a,

Substituting

this

result

into

the

equation

under

consideration

and

dividing

through

by

wA 6x

gives

Ad,

tP

uOu,10u

:__

Ox'

'

wA

g}x'

g

0t

rplwAisrlwmwhere

z

is

the

hydraulic

mean

depth

and

this term

is

denoted

byi;

so:

ad

u0u

10u

-+--+--+r-I=u

Ox

gOx g0t

'J

This equation

is

more

often

written

as follows.

ad

Q*A

* E:o

I

a**u

ar

or

where

E:

s(j-i).

The

two

equations,

known

as

the Saint

Venant

[15]

equations

are:

ad

c2 0u

ad

U-*-:-*=-:U,-dx

80x

0t

ad

9*9*E:o

.

I

ar*'a*

at

that

occurs

in channel

flow

problems,

there

are

certain

complications

in

the

use of

the

channel

flow

equations

that

do

not

arise

with

the

waterhammer

equations-

7.4

THE CHARACTERISTIC

FORMS

First

multiply

equation

(7.1)

(the continuity

equation)

by

8:

ad

,r! +4:o

.

Suar+c

or

ot

equation

(7.2)

(the dynamic

equation)

by

c:

Ad

0u

,s

ia

us

i*

,

u*

E:0

Add

the

two

equations:

/ a a\ /

a a\

('+,)

*.;)

gd+c

(r.*,);.;)

u*cE-o

On

p.

000

it

was shown

that

d0

d,r

a0

,

a0

dr

dt

0x

0t

For

the

very special

condition

that

dxldt=

u

*

c the

can

be

written

as

t

*r+'#

*cE-o

.

These equations

can

be

solved

for

a channel

by

a

variety of

finite

difference

methods

some of

which

will be

given later.

It is

possible

to

obtain

their

characteristic

forms

quite easily,

and

it

will

then

be

seen

that

these

equations

are exactly

the

same

as the

waterhammer

equations

and

the

same

techniquer

is

*"t" used

to solve

the

waterhammer

problem can

be

employed

to

solve the

uniteady

channel

flow

problem.

Because

of

the much

lower

wave

speed

(7.3)

Examining

the

(d/d|kd) term,

it equals

g(ddJdt and

as

8A:

b'6d

it follows

that

ddtdt:

(lib,)

@eni.This

implies

thit

d6:

dd

and

for

a

prismoidal

channel

this

is

correct.

The

term

thus

becomis

(g/b,)

(dAldt). When

the

whole

equation

is

divided

by c

the

term

becomes

(g/b.

Q@ent

and,

as c2:

86

and

6

:

Alb",

then

the

term

reduces

to

(cl

A)(dAl

dt.

The equation

therefore

is

cdA

du

;i

*;

*

E:o

Subtracting

the

two

modified

versions

of equations

(7.1) and

(7.2)

gives a slightly

different

result.

r52

Unsteady

flow in

open channels

lch.

7

For

the special condition

that dxldl

-

u

-

c the resulting equation can be written

AS

Generally

(7.4),

Q.aa\

and

(7.s), (7.sa)

Another

version

of this

equation can be obtained by another

manipulation of

the

first

term in

equations

(7.5)

and

(7.5a).

Reconsidering equation

(7.3);

the first

term is

(dldt)(gd). gd:

c2 andthe

differential of c2 isZc(dcldr)

so

the equation becomes

2dc du

&

+a*u-0.

Sec.

7.61

SuPercritical

flow

("'

-f.)#.ix*E:o

153

(7.e)

All these

forms apply to channels of

any

prismoidal

cross-section.

The integrated form of

the last equation is sometimes

preferred:

u+2c* Et:a

constant.

Another form of

equations

(7.4)

and

(7.5)

is

sometimes

preferred

because

it is

claimed to be more conservative.

It uses A and

Q

as

variables

instead of

u and ^A.The

equations

are

When u: c,the

flow

is said

to be in critical

state. When

u is less than

c, it is said

to

be

in subcritical

state

and,

when u

is

greater than c, it is said

to

be in supercritical

state.

Other

terms have

been

used in

the

past

such

as tranquil

or streaming

flow

for

subcritical

flows

and shooting

or torrential

for supercritical

flow. This terminology

is

rapidly

becoming

obsolescent.

7.5 SUBCRITICAL

FLOW

In subcritical

flows,

waves

travel

faster

than

the liquid itself;

so they can

progress

in

either

direction,

i.e.

both

upstream

and

downstream.

For this

reason a disturbance

in

a

flow can travel

in

both

directions,

causing

changes

in

velocities and depths.

The

profile

of

such

a flow

is determined

by

conditions

both

upstream and

downstream.

The boundary

conditions

at

both ends

of a reach

have their effect

upon

the

reach.

Note that

a reach

is a section

of

channel

in

which

properties

such

as roughness,

bed

slope

and cross

section

are

constant.

7.6 STJPERCRITICALFLOW

In

supercritical

flows,

waves travel

slower

than the

liquid

and are

unable to

progress

upstream.

In

such

cases

the

flow is only

affected by

upstream

conditions.

There

is an

important

qualification

to

this statement:

the

waves being

discussed

are

infinitesi-

mally

small

waves

and

what has

been

said

certainly applies

to

these. However,

a

travelling

surge

(or

moving

hydraulic

jump)

can travel considerably

faster

than

such

a

wave, having

a

larger

celerity,

and such

waves may travel

in either

direction

if

the

degree

of supercriticality

of

flow is

not sufficiently

large.

In

waterhammer,

the

acoustic

wave

speed is

far larger

than the

velocity of

the

liquid, c:

1400

m/s and

u usually

does

not exceed

3 m/s,

so the

Mach

number

of

the

liquid

is

very small

and

always

far

smaller

than

unity.

(The

Mach

number equals

u/c.)

There

can

be only

the

smallest

possibility of having

a supersonic

flow.

(The

possibility cannot

be

dismissed

completely

because the

author

has heard of

very

high

ipeed

liquids,

delivered

through

pipelines

of

small diameter,

and

used to cut

metal

and

ceramics.

The

pipelines used

are

very short

and small

and

operate

under

very

large

pressures

and

are

in

no

way typical

of any other

sort

of

pipeline.) 40

years

ago

the Froude

number

was

defined

as

being

uzlg} because

when it appears

in

expres-

sions

it almost

always

occurs

in this

form.

Nowadays,

because

of the similarity

of

free

surface

flow

to compressible

bounded

flow

(the

analogy

between

the two

is total

and

perfect) the equivalent

number

to

the

Mach number

in free surface

theory

-

the

Froude

number

-

is

written

as u/c

where

t:

VF

or

Dt{gd.

As the

slopes

of the

characteristic

lines

arc dtldx

:

ll(u

+

c) the

two types

of

flow

give very different

patterns in the

t

versus.r space.

In

subcritical

flow the

positive

iharacteristic

has a

positive slope

(dtldt:ll(u +

c)) but

the negative

characteristic

has a

negative

slope

(dtldx:

Il(u

-

c))

because c is

greater than

u. In supercritical

-;#*#*

E:o

dx

a:

u*'

cdA du

tzil

*t * E:0

Also,

d.r

E:,

lC

,

9trdt

+ E:o

dt-

-

dt

(7.6)

(7.6a)

(7.7),

(7.7a)

d.r O

-72!

7

dt A--

'

(7.8)

154

Unsteady

flow

in

open channels

'

[ch.7

positive

slope

as u

is

about subcritical

and

flow both the

positive and the

negative characteristics

have

greater

than

c.

This, of course,

infers the statements

made

supercritical

fl ows above.

Two important

points

emerge

frorn Figs.7.4 and7.5.

XR

Fig. 7.5

-

Supercritical

flow.

(1)

The

interpolative

procedures used to establish

the

velocity

and celerity

values at

points

R and S in

sub-critical

flow

must calculate the

values

in

the upstream

and

the downstream

Ax

values

respectively and in supercritical flow

they must

both

be

calculated

in the

upstream

A.r.

(2)

When

the flow

is supercritical,

the solution

of

the upstream boundary condition

cannot use

any

characteristic

equations

but,

when the

flow is subcritical,

the

negative

characteristic

is

used,

7.6

CHARACTERISTICS

WITHOUT THE

E

TERM

In

near-horizontal

channels

with very small friction, i andT

are

nearly

zero; so the

E

term can,

under these

circumstances,

be neglected. Alternatively,

when a flow

is at

near uniform

flow conditions

the

value

of

i

-

jis

very

small

so that, again,

E can

be

neglected. Under

these

conditions

it becomes

possible

to make

predictions

which

cannot be

made if

the

E term

has to be taken into account.

In the

earlier

sections

of

this chapter it

is shown

that

the characteristic

equations can be written

D-C

If.

E L,t can

be

treated

as

negligible

then

the equations

reduce

to

o+k:

a constant,

From

these

results,

valuable

relationships

can,

very

easily,

be deduced-

Along

a

positive

characteristic

line,

u *

Zcis

constant.

Similarly,

along

a

negative

characteris-

tic line

the

u

-2c

term

is

constant.

Consider

the

area

ABCD

in

Fig.

7

.6 made

up

of the

intersections

of

two

C*

and

two

C-

characteristics.

C*

familY

Fig.7.6

-

Frictionless

characteristic

plot.

Along

the

C-characteristics,

u ^

-Zc,

:

u^

-2c^

Sec.

7.61

Characteristics

without

the

E

term

155

dr

--:lt*c

dt

and

u-2c+ELt:

aconstant,

P

-"T\

,/l\

rl\r

XR

N S Y

Fig.7.4

-

Subcritical flow.

P

11

,1,

d.r

a-

d-r

.:-:DAC

dt

N

zone

of

quiet

dt

1

dx

n0*t0

u*2c*ELT=aconstant,

Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

Подождите немного. Документ загружается.