Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

196

Finite difference methods

lch.

8

obtained

from the

upstream

and downstream

characteristics together

with

the

boundary

conditions.

The

resultingZn equations must then be

solved

to

give

the

pairs

of

values for

the

later time required at each of

the n

nodes.

8.6.2

The

second Strelkov

method

The second Strelkov

method specifies

slightly different finite difference forms for the

partial

derivatives

in the

St

Venant Equations.

These

are

ui+

t

+t-u;-t

+l

dr*,

2Lx

*r-

dr-,

2Lx

These expressions

can be

used in the

same

way as those derived for the

waterhammer

case above.

I.7

THE PREISSMAI\N-SOGREAH

MPLICIT

SCHEME

This schleme

was developed to enable even

larger

At

values to

be used than

are

possible with

explicit

methods.

Regarding this

point

it is

worth

mentioning that,

when

very

large

river schemes

are being analysed,

the duration of the simulations

can

be

very

large. There

is, then,

a

very

strong incentive

to

use

very

large Arvalues and

implicit

methods are capable

of

handling very

large At

values

indeed. It should be

remembered

that implicit

methods cannot handle supercritical flows accurately

nor

can

they deal

with rapidly

changing boundary conditions unless the Ar

values

are

correspondingly

reduced.

However, they are extremely useful when

very long

simulated times

are to be

analysed. It is claimed that the analysis of sewer networks

is

best

done

with

implicit

methods.

This

is because,

as the

depth

increases

in a

sewer

with a circular cross-section,

the surface

breadth

diminishes,

eventually

becoming

zero

when

the

depth equals

or exceeds the sewer's diameter. As the

wave

speed

equals

VkD)

and 6 is

the ratio of

the

flow area to the

surface

breadth, the

wave

speed

becomes

infinite. In implicit

methods the wave

speed is not

involved, whereas in

characteristic

methods

the

wave

speed is a

parameter

of major importance.

So

irnplicit methods are suitable

for dealing with

analyses of this type, but it should

always be remembered

that

these methods

cannot handle supercritical

flows and

sewage

networks,

very

frequently

indeed,

experience supercritical flow conditions.

It

must

still be

remembered,

however, that

implicit

and

explicit

finite difference

methods can

pass

shocks,

i.e.

hydraulic

jumps,

and these are common in sewerage

networks. The

pros

and cons

of

using implicit

methods are

therefore

complex

and it

may

well

be thought

that,

for such complicated circumstances, the method of

Sec.8.7l

The

Preissmann-sogreah

implicit

scheme

r97

characteristics

may

have

something

to

offer.

tf

this

method

is chosen,

the

tracking

of

any

hydraulic

jumps

must

be

undertaken

and

supercritical

flow

sections

must

be

analysed

approPriatelY.

E.?;l

Ttre

Preissman

implicit

scieme

The

discretization

of

the

-dependent

variables

and

their

derivatives

as

suggested

by

Preissman

are

given below:

f,.i

:|{f,*r,,

*,

+

f,,i).

ry

(f,*

r'i

*

f,,i)'

{.:"-*+(1-q*'

ll

-f,*r,i*r-

fr*r,i

*

f

,,,*t-

ft,'

Ot

ZLt

0 is

a

weighting

eoefficient

which

must

lie

between

zero

and

unity'

Each

of

the

dependent

variables

in

the

continuity

and

dynamic

equations

together

with

its

associated

derivatives

can

now

be

replaced

T

th9

appropriate

eq"uation

by

one

of

the

expressions

just

specified,/b9ing

replaced

by

the

dependent

nuriubl"

und",

consideration.

Reduction

of

the

resulting

expressions

and

substitut-

ing

f

:

'l-,2,3,

4,

. .

.

glves a system

of

implicit

equations

which

together

with

end

characteristics

and

boindary

conditions

cin

be solved

for

depth

and

flow

at

each

node

along

the

reach.

The

system

is always

stable

if_0

is chosen

to

lie between

0.5

and

L.0

and

isilways

unstable

when

0

is

lesithan

0.5.

When

0

is

between

0-5

and

0'55,

parasitic

oscillations

have

been

reported

but

these

only

occut

il-

+9

absence

of

hction.

By

using

larger

values

of

0

-

greater

than

0.66

-

artificial

damping

is

introduced;

so

tf,e

rJcommended

procedure

is

to

use

0

=

0'5

when

there

are

significant

resistance

terms

prereni

and

0

=

0.6

or

larger

for

less

frictional

circumstances.

For

further

details

of explicit

and

implicit

methods

the

reader

is

referred

to

the

book

(lnsteady

flow

in

open

channels

edited

by

K. Mahmood

and

V'

Yevjevisch

published

by

lVater

Resources

Publications,

PO

Box

303,

Fort

Cottins,

Colorado

'1OSZZ,USA.

The

Lax

Wendroff,

StrelkoV

methods

and

the

Preissmenn

method

all

use

i to

denote

spatial

location

and

j

to

denote

timewise

location

whereas

the

I-eap

Frog

method

,ei"rs"s

this

practicl.

ttris

follows

the

practice

employed

in

the

sources.

0u

0.r

ad

ar-

+l

0r

Lt

Resonance

9.1

INTRODUCTION

Resonance

is

of

common occurrence

in

pipe

networks although

not in channels. In

channels, resonance takes the form

of seiching which

is similar to the

motion that is

generated

when

a forcing

longitudinal

oscillation is applied by hand

to the

water

in

a

bathtub. It occurs in

reservoirs

and

even larger bodies

of water. Perhaps

the most

famous case

of it is in the Adriatic

Sea which

can be

set

into

seiching by

winds

and

pressure

distributions created in storms.

It is important

in that, when

the sea is

seiching, the city of

Venice can

be submerged,

at least in

part.

In

pipe

networks,

similar resonant effects

can

be

generated

although at much

higher frequencies. The

pressures

that resonance

generates

can be excessively

large

and cause

pipe

bursts. In

some machines

in which

pipe

networks

occur, resonant

behaviour can cause

vibrations.

These may be unacceptable

because

of the noise that

they

generate

or

because of the risk

to

the

physical

integrity

of

the machine.

When

a

pressure

wave is sent

up a

pipeline

at

the

upstream

end of which there is a

reseloir, it reflects

at

the

reservoir

completely

and

negatively

and this negative wave

is

then

returned to the downstream

end.

The exact details

of this

process

are

described in Chapter

L on

pp.

31 to

35. If at the moment

of the return of the

negatively reflected

wave a reinforcing

wave is applied

to the downstream end, the

process

will

be

repeated and the

energy

of compression

of the fluid and

and

the

energy of

distension of the

pipe

will be

increased. This

will cause the

pressure

to

increase and,

unless there is a dissipative

process

such as

friction, the

pressure

will

continue to increase

until the

pipe

bursts.

The

situation is very

similar

indeed

to

what

happens in musical instruments such as organs

or flutes, in which

standing waves are

formed. Of course,

the

frequencies of such oscillations will

be

very

low

compared

with

those

of sound. The

same

phenomena

that

arise in the

case of musical

instruments can arise in

pipe

networks.

The

fundamental

frequency

may be

gener-

ated

in either

case

and the

overtones or harmonics may also be

excited.

There

are

many ways in which

the

necessary

forcing

oscillations can

arise. One of the

Sec.9.1l

Introduction

199

commonest,

which

almost

everyone

will have

encountered,

is

the oscillating

ball

valve.

These

valves occur

in

the expansion

tank

of any

central

heating

system

and

also,

in the UK,

in

the

hot

water

supply

tank

(although

such antiquated

technology

is

now under

critical

re-evaluation).

junction

that

it

encounters.

The

pressure rise

in

the

pipe is also

applied

to the

nearly

Ltosed

rubber

valve

face

and

the

force

that

it exerts

will

force

the

ball

back

under

the

water surface.

Thus

there

are

two

springs

acting:

the

buoyant

force

acting

on

the

ball

and the

compression

of

the

rubber

disc on

the face

of

the

valve.

There

are two

masses

involved

in

the

oscillation:

one

is the

mass

of

the

ball

and

the

operating

arm

and

the

start

into

resonance

about

an

hour

after

he had

gone to

bed and

would

generate so

valve

had

to

be closed

before

each

perfonnance,

and

re-opened

after

it,

to ensure

that

this

most

unacceptable

interruption

did

not

occu.

The

solution

to

such

resonant

events

is to

alter

(i)

the

spring

stiffness,

(ii)

the system's

mass

and

(iiD

the damping

of

the

sYstem.

By changing

the

valve

facing,

which

is

made of

rubber,

the

resonant

frequency

of

the

u"tn"

is

itteied.

This

is

beciuse

the

rubber

face

of

the

valve acts

as

the

spring

in the

spring-mass

system

and

replacing

the

rubber

facing

alters the

rubber's

elasticity.

^

1.fir seroni

parameter

ittat

-iy

be

changed

is

the mass

of

the

oscillatory

part

of

200

Resonance

lch.

e

the system. Adding

mass to the

operating

arm

-for

instance by

attaching

a stiffplate

to the base

of the ball

-will

make the oscillation

have

a

lower

frequency which,

in all

probability,

will no longer give

rise to resonance.

This

particular

technique

has

other

benefits:

the

plate

attached

to the base

of the ball

of

the valve will

cause a

considerable increase

in the

energy

lost

from

the

vibration

in fuid friction,

so

increasing the damping

of the

vibration.

This

method of solving

the

problem

of the

oscillating

valve

is sufficiently recognized

for

manufacturers

of the balls

of

such

valves to

make a

flat

plate-like

float which will

provide

greater

damping

than

does a

spherical

ball.

One

further

thing that

can be done to

detune

such resonant

behaviour

is to

change

the diameter

of

the

supply

pipe.

A

pipe

of

larger

diameter

will

have

smaller

velocities

in it and so any velocity

changes that

occur within

it

will

be

correspondingly

smaller,

Ieading

to

smaller

pressure

fluctuations

to drive

the

resonance.

This homely illustration

has many analogues

in

the

world

of hydroelectric power

generation

and in the field

of water distribution.

Wind-generated

waves

on

the

surface of a reservoir can

cause small

pressure

fluctuations

over the

entrance to a

pipe

network which

may then be

set into resonance. Valves

in large

pipelines

are usually

of the butterfly type

and are sealed, when

closed,

by a rubber

seal around the

periphery

of the

valve

leaf. This

rubber

seal is usually inflated

by

either the liquid in

the

pipeline

or some other liquid

-

usually oil. If the

rubber

seal is damaged

and the

Pressure

in

it is lost, the seal may

start to

vibrate

in

a

manner

sometimes

called flutter.

Such

a

vibration

is

caused by leakage over the

seal, the associated

Bernoulli

effect

causing a

drop in

pressure

which makes

the seal

expand, thereby

shutting off the

leakage. When the leakage

stops, the

pressure

rises

and

the

seal

shrinks, so causing

the leakage

to

restart.

This intermittent leakage generates

a fluctuating

flow which,

in

turn,

causes an oscillating

pressure

which

could

be the forcing vibration

to drive a

resonance.

It

is not

only that a frequency

exists at which

the

network may resonate

which is

so

dangerous

but

that many harmonics

of

such a frequency

may operate to

cause

resonance

also.

Servo-controlled

valves

can

easily be set into

vibration

by

slack in the mechanism

or by

an

unhappy

choice of the servo mechanism's

characteristics.

If the frequency

of

the fundamental

or that of any

of the

harmonics

of this

vibration

match the

resonant

frequency

of

the network then

resonance may

occur.

9.2

ANALYTIC

METHODS

AVAILABLE

Resonance analysis can

be

performed

by four

methods.

(a)

The

characteristics method.

(b)

The

hydraulic impedance method.

(c)

The

transfer matrix method.

(d)

The

Fourier analysis method.

9.3 TIIE

CHARACTERISTICS

METHOD

The method already described

can be used

to calculate

pressure

magnitudes in

resonant

conditions. It is

quite

impossible

to use this

method

to

investigate

the

Sec.9.4l

The

hydraulic

impedance

method

description

of

friction

but other

methods

linearize

friction

and

consequently

produce

less

accurate

results.

The

characteristics

method

produces the

highest

grade of

results

but is only

usable

once

the

frequency

of the

applied

resonant

frequency

has

been

determined.

9.4

THE HYDRAULIC

IMPEDANCE

METIIOD

9.4.1

The analogy

between

electrical

and

hydraulic

impedance

The

analogy

between

electrical

currents

and

hydraulic

flows

has long been

recog-

nized.

The major

difference

between

them

lies

in the

dissipative

mechanisms

present

in

the two

phenomena.

It is

true

that electrical

theory

can

include

such

phenomena

as

radiance

and

leakance

and

there

are

no

analogous

phenomena in

hydraulic

theory-

, r -r- -r rL --- :^ -^ r^^l-^-^^ :- ^ L-'l-^"li^-i^^li-a h'r* flrp

qnqlnrrrr

at

least, one

nopes

Inat

tner9

ls llu

tcartalll9|;

lu

<l llyurauur/

PrPvrruw

-

trrtr

rrrv

4uqrv6J

between

the

fluid

properties of

a

pipeline

and

the electrical

properties

of a

trans-

mission

line

can

-b"

ieen

quite

clearly,

once

the analogy

has been

stated

in

mathematical

form.

20r

The equations

applicable

to

a transmission

line are

av

1ai

ar

-

a

a*:u

and

AV

LAi

;+E+R.1i:0

(e.1)

where

V is

the

voltage

and

i is the

current.

R.,

is the

electrical

resistance

per

unit

lenglh

of

the

line,

C

is the

capacitance

of

the

line

per

unit

length

and

L is

the

inductance

per unit

length.

The

equations

applicable

to

a

pipeline

are

(e.2)

(e.3)

(e.4)

The

terms

in

these

equations

are

the same

as

those

used elsewhere

in

this

book.

h

is

seen

as analogous

to the

voltage

V andthe

flowAv

is

seen

as analogous

to

the

)tldt

term

provided

that

c is large.

Equations

(9.3)

and

(9.4)

become

Ah c2 0e_o

--{--

0t'

gAlx

ah

+

1, 0q

*Zfqlql:o

a*-

gA

UTW-''

202

Resonance

lch.

e

current

i. If the u(1hlAfi

term in equation

(9.3)

can

be neglected and

the

(u/g) (0u/0x)

term in equation

(9.a)

can be neglected

and the zfulullgdterm

can be linearized

then

the analogy

can be

seen

to be exact.

The

u(dlrlOx) term

is

small

compared

with the 0hl0t

term if

the

wave

speed

is

large : This istecause

O/r/Er

:

(u*

e{O/rlOr)

;

so

;

if itean

be

assurned that eis large in

comparison

with u, the o(}hllx)

term can be neglected.

By the same argument,

the

u(OulO-r)

term in equation

(9.4) can be seen to be negligible

in comparison

with

the

The

value

ot

OhlOVis

the

hydraulic

gradient

and

therefore

equals

-Zfqlqltgdez.

fn"

u"f"r

of.

OElat:O

as

the

steady

liead

component

does

not

change

with time'

Equation

(9.5) becomes

A(h+h')

*cz

d(q+q')

-o

0t

gA 0x

and this

reduces

to

Oh'

*!V=0.

Q3)

0r

gA

0x

Equation

(9.6)

O(E

+

h')

*

t

O(q

+

q')

*zflq

+

q')|,(F

+

q'\l

-

^

-ar

Ot

?dA'

becomes

-

zfqlql

*Oh' *

L

Oq'

*hf(q

+

q')l(g

+

q')l

-

,

dAz

'

0r

'

gA 0t

gdA"

Sec.9.4l

The

hydraulic

imPedance

method

203

(e.8)

For

the

analogy

between

friction

and

electrical

resistance

to

hold,

the

value

of/must

be

seen

as

a

constant,

which

is

not

true.

However,

fqlql

can

be

rewritten

as

fsq"

where/s

is

a true

constant

and

n

lies

betweenL.Ts

and

2.0.

fniierm

(q

+

q,)2 can

be

expanded

by

the

binomial

theorem:

(E

+

q')'

:qn

+

n4q'

*ffiu*rq'+

.

. .

.

If

q'

is small

compared

with

q,

second-order

terms

can

be

ignored;

so

2fo(4+q')"

=2f&" *Znf&"-'q' .

7dA"

gDA"

gdA"

Therefore

equation

(9.8) becomes

-2f&"

-Oh' *

|

dq'

*Zfoq" *Znf&"-'q'

-0

gdA"

'

0x

'

gA

0t

gdA"

which

reduces

to

(e.5)

(e.6)

9.4.2

The linearization

of

r,he

2,fqlql/A2gdtprm

If the flow

q

is thought

of

as being made

up

of

a steady

flow and

an

oscillating

component

of flow, the

term can

be linearized. Thus

let

q: q

*

q' where

q

is the

steady

state component

of

flow

and

q'

is the unsteady flow

component. So

As

?

is a steady

quantity and

invariant

with

x,0Ql0x

will be zero. So

Similarly

0q:Oq

-Oq'

qt

0r'

0t'

Now OQl)t: 0

as the

flow

Q

is

steady

and does not

vary

with time;

so

0q

:0q,

0r

0t'

This

process

can

be

repeated

with the

variable

h.

h can

be

split

up into two

components:

a steady

and

an unsteady component. So

Oq

:Oq

*0q'

A

'

dx ox

ox

0q:0q,

A

dx dx

h:h+h'

lch.

e

(e.e)

(e.7)

(e.e)

Sec.

9.41

Then,

differentiating

with respect

to x,

The

hydraulic

imPedance

method

205

If the

rcrm

2nffii"-algdA- is denotedty R

which

is thehydraulic

resistance, the

hydraulic

equations

reduce to

204

Resonance

Ah'

1

dq'

,2nf&"-'q'

-J-

Ox

gA

Ot

gdA^

-

0

Ah' c'04'_o

&

+

gA

ar-u'

#.hY*Rq':s

Comparing

these equations

with

the electrical equations

*:-*(#*^n')

#:-sA(*.#)

av iat

;;*;-:u,

dT LdX

l-,, +

I-'

LI L

Oq'

-gA

0h'

--L:

--:-

-

0x

c2

0t

from

equation

(9.7).

So

I

azh'

,

Roq',

:-

c2 otz

oxz

ox

Azh'

_gRA

0h'

_

I

Oxz

c2

0t

c2

H.

t#.R.1i:0,

it can

be seen

that the

hydraulic equivalent of the capacitance

per

unit length C

is

gAlcz,

the hydraulic equivalent

to the inductance L

per

unit length is llgA and

the

hydraulic

equivalent

to

the

resistance R.1

per

unit

length

is

R which was defined

above

as2nffi"-LlgdA".

If the

flow

is laminar

R becomes32vlgdzA from the Hagen-Poiseuille formula.

fte.fo

form

used in

this development is the British form

but

it is known in the USA

as

the

Fanning/. The

form more commonly used in the

USA

is four times

larger than

the

British

form.

The British equation

for the head loss due to friction in a turbulent

flow is

h:4fLuzl2gd

whereas

in the USA

it is /lt

-fLuzlZgd.

9.4.3

The

solution of the

linearized waterhammer

equation

First

differentiate

equation

(9.7)

with

respect to time:

A2h,

_c2

02q,

@:

gA

arat'

0q'

_-gA)h'

0.r 0r

cz )tz

and, rearranging

equation

(9.9),

-0.

(e.10)

This

is the

wave equation'

If

an

oscillatory

wave

has

a

constant

wave

speed,

its

amplitude

will

not

change

with time

at any

particular

point on

the

pipetine

although

it

may

attenuate

over

the

length

of

the

pipeline.

If a

sinusoidalty

varying

pressure

is applied

to

the

pipe at

its

upstream

end

a

solution

of

equation

(9.10)

must

be

h':Heitu

where .Fl

is

the

amplitude

of

the

wave.

At

x

=

0,

h'

,:o--

Ho eia''

Atx=xr,

a2h'

0t2

ht*r:

Or,

"tn'

206

Resonance

The reader

is reminded

at this point

that

eitu:

cos(er)

+ i

sin(er) where

and cl

:

2nf where

/

is the frequency

of

the

oscillation.

Therefore

lch.

e

i:V-1

Sec.

9.41

The

hydraulic

impedance

method

Crm2

e^

:

^fzCt

e*.

Therefore

207

a2h'

azH

-

:

-

alsat

dxz

0x2'

'

ah'

.n

;:

if)r/

eio"

a2h'

i

=

-

{'2H

ei')t '

Substituting

these results

into

equation

(9.10),

azH

pRA

o2H

5p

ertzt

-fiQn

siarl-f

eitu:0.

So

u='4-

:#(.9+

in)a.

1xz

cz

\Sa

,".J.,.

Denote

(AS{U:')

b

(AE$

+

n] by

y'.

Then

ffi:r'u.

A2Er

--

Crmm2

e*.

dx

m2:

yz

and

m:

!T.

The

required

solution

is

thus

H

:

aeY'

*

b

e-t'

where

a and

b areconstants.

So

h'

--(a

er'*

6

.-rx1

sicu

(e.13)

To obtain

the solutionfor

q',differentiate

equation

(9.13) with

respect

to time:

#:ie(a

er'*,

"-r')

eifr.

(e.11)

From

equation

(9.7).

Oq'

-

gA

Oh'

-:

Ox

c2

0r'

Therefore

(e.12)

In the

electrical

theory

of transmission

lines,

y

is called

the

propagation

constant.

Equation (9.12)

is

called

the harmonic

equation.

A solution

of

equation

(9.12)

is of the

form

H:

Cr e*

and

so

q,

-#

e,*(a

el,

-

b e-r,).

-

rc-"l

This

is the

general solution

of the

wave equation

for

any sinusoidal

oscillation.

9.4.4

The evaluation

of

1

Now

y

is complex,

as

can

be

seen

from

its

definition

(equations

(9.11,)

and

(9.12));so

it

will have

the

form

q,

:+,r,

"'{t

a et,

*b e

_r,)

&

(e.14)

So

Y:a+iP

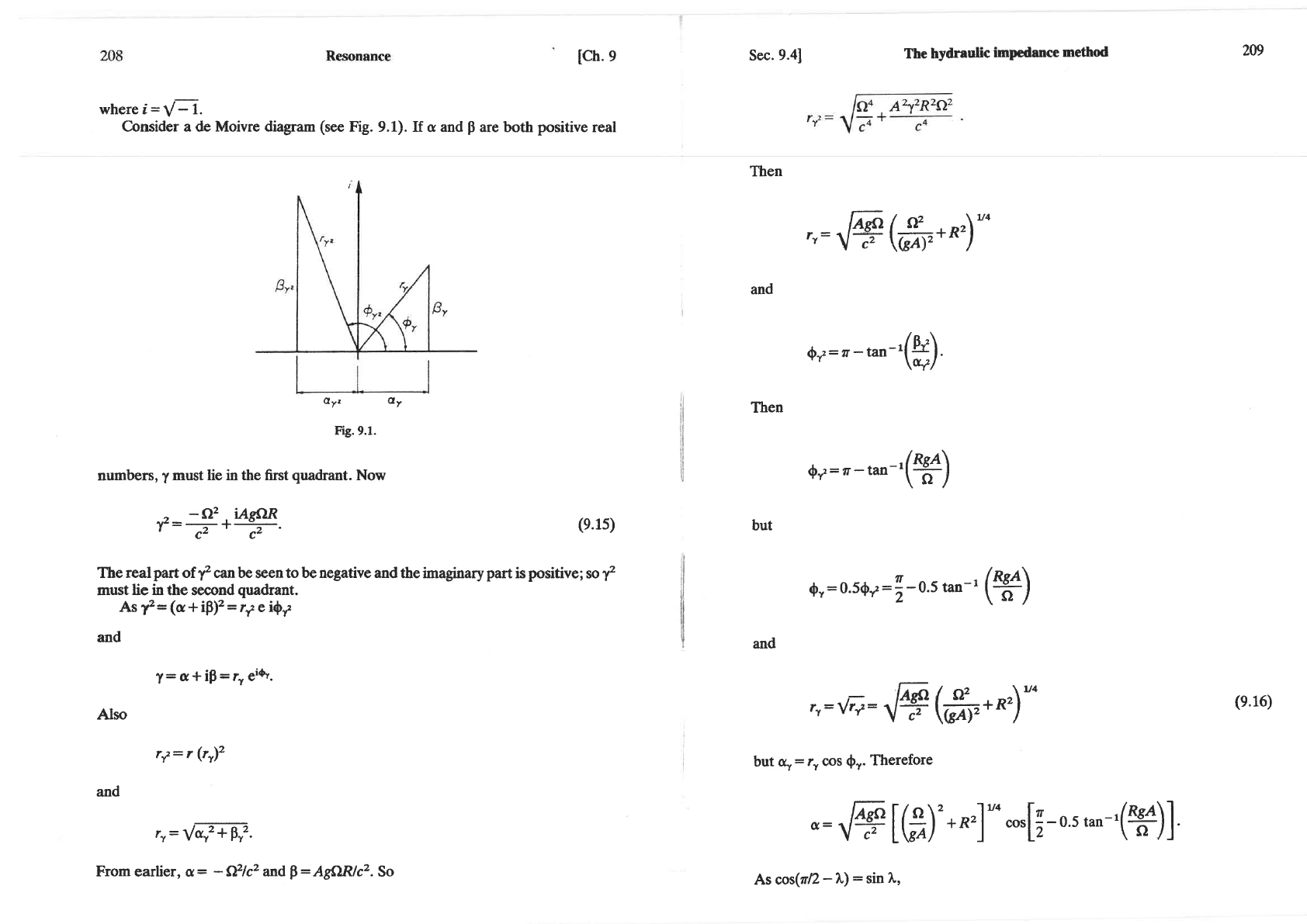
lch.

e

wheref=V-1.

C-onsider a de Moivre diagram

(see

Fig. 9.1). If

c

and

p

are both

positive

real

Sec.9.al

The hydraulic

im@ance

method

2W

Then

and

Then

but

,,:Jry(#.*')"'

if

:zr-tan-1(#)

Qy,

Cty

Fig.9.1.

numbers,

y

must lie in the first

quadrant.

Now

nr._-Q'+iA80R

'c2cZ

(e.ts)

The

realpart of

f

can be

seento

benegative andtheinraginarypart

ispositive; so'f

must

ti'c in

the second

quadrant.

Asf=(c+i$2=rlet6f

and

T=

c

+ ifl= r, eifr.

Aho

rrz: r

(rr)2

and

rr:t/o--r? +Pr''

Frorn earlier, s=

-

dfilcz and

p

:AgSlRlc2.

So

Q,=o.5ol

=;,-0.5

tan-l

(Y)

but ory

-

r7 cos

$".

Therefore

*:

r{rytffi)'

* *']

"-

*,[l

-

o.s'*-'(Y)].

As cos(rif2

-

lu)

:

sin

?u,

and

(e.16)

sr=n_tan_1(Y)

,,-,,/G-

a[ry

(#*^r*

lch.

e

(e.17)

Sec.9.4l

The

hydraulic

impedance

method

ztl

2r0

Resonance

3)'*

^']

"o,in[0.r,*

-'(Y)

]

and

pr:

r, sin

0.

So

(e.18)

9.4.5

The impedance

concept

In

an

electrical

network the

risk

of

resonance

can be assessed by investigating

the way

in

which

the impedance at

a

point

in the network varies with the frequency of the

voltage

applied

to the network.

The concept

of impedance, in some

ways,

resembles

the

idea

of resistance. The

resistance of a section

of

the network is

the

ratio of the

drop of

voltage

over the section

of

the

network to the current through

it.

The

concept

of resistance

comes

from the study of

direct

current. In alternating

current theory it is

not

sufficient,

as other

phenomena

are

present

in which energy is stored in magnetic

and

electrical

fields, i.e.

in inductive and capacitive effects and, in

high voltage

networks,

energy

is lost in radiance

and leakance

effects. In alternating

networks it is

therefore necessary

to employ

a rather more complex definition of the ratio of

the

voltage

drop

to the current.

The ratio is called the impedance, which is a

word

which

carries many of the overtones

of

resistance

but, because of the energy storage effects

in

inductance

and capacitance,

it is dependent upon the frequency of the applied

voltage.

Thus,

at any

point

in the network, the

impedance

will have a

small

or large

value, dependent, in a

very non-linear way, upon the frequency of the applied

voltage. In Fig.

9.2,at1pical

Zversus/plot

illustrates this

point.

Zisthe impedance

and/is the frequency.

It can be seen

that

at a number of defined frequency

values

the

value of

Z becomes

very

large.

At

such frequencies the

network is said to be

resonating

and these conditions

correspond to the

generation

of

very large voltages

at the

point

in

the network

for which the

analysis was

performed.

In

exactly

the sane

way,

a similar

value

can be

specffied

in the hydraulic

circumstance

which

@rrespondsvery

closely

to the concept of

electrical impedance.

Whereas electricd

impedance

is defined

as Vli, hydraulic impedance

is

defined as

h'lq'

.

V is the alternating

voltage

at the

point

in the network and

i

is

the alternating

current

passing

at the

point

in the electrical network; lr'is

the oscillatory

component

of the

piezometric

head

and

q'

is

the

oscillatory component of flow

passing

the

point

in

the

hydraulic

network.

In both types

of

network

the steady components

of the

variables is ignored.

So

h'

Zfu):--\"/

a'

'

Therefore

L

f

Fig. 9.2

-

Impedance

versus

frequency

in an electrical

circuit

containing

resistance,

inductance

and caoacitance.

(e.1e)

(e.20)

has the

dimensions

of

impedance

and

is denoted

by

Z"the

characteristic

impedance:

the term

(a

er,

+ b

e-rtt(a

sr'

-

b e-r')

on

the

right-hand

side

of the

expression

is

dimensionless.

At the

end

of

a

very long

pipeline,

.r

goes

to

infinity

and

so

the

terms

go

to

zero.

Then

Z(x):

-

Z"'

So

-

Z.is

the impedance

of

an

infinitely

long

pipeline

extending

in the

x direction

and

Z"ii

ttre impebance

of

an infinitely

long

pipeline extending

in the

-

r

direction.

It

will now

be seen

that,

when

an oscillatory

head is

applied

to

a

network

at

a

frequency

that

makes

the

impedance

of

the

network equal

to

-

Z",the

applied

wave

2t2

Resonance

lch.

e

will

enter the

network

without

reflection.

In

electrical networks

this

property

of the

characteristic

impedance is

of

great

importance. When

the

play-back

head

of

a

gramophone

is connected to an

amplifier and the signal that it

generates

is fed to the

amplifier,

if the frequency presented

creates

an impedance which

is

equal

to

-

2.,

there

ulillte

norefleetion

oftlre

applied

signal andso-nodistortion

caused

by

connecting the

two devices. This

is

the

explanation

of the frequently used phrase

that

it is necessary

to match the

impedance of the

play-back

head to the amplifier when

connecting up

a hi-fi system

Substituting the

value

of

y

into the

expression for Z.

gives

Sec.9.4l

The

hydraulic

impedance

method

At the sending

end

where r:0,

h'o: Ho

at*

:

Hs, ettu

and

e'o:

Qo

e'*

:

Qs

aitu.

From equation

(9.13),

h'o: H,

at*

-

(a

et'+

b e-")

e'''.

Hs:a*

b'

Similarly

for

q'from equation

(9.14),

eitu

(o-

b).

a:0.5(FIs

-

Z.Qs)

and

b:0.5(Hs+

Z.Q).

Therefore

(e.2r)

2L3

(e.22)

(e.23)

9.4.6 Receiving

and sending ends

Following

the

practice

used in transmission

line theory

the end

of

the

pipeline

atx

=

0

will be

thought

of

as

a sending end and

the receiving

end

will

be

considered as

being

__atx: t

(Fig.

9.3)=

In other words,

the location

of the forcing

oscillation

wi!!

be

5

H(x) R

''J

Fig.

9.3

-

Receiving and sending ends. S denotes

a sending end and R denotes

a receiving end.

thought

of as being located at the upstream

end of the

pipeline.

Readers

are

warned

that

in some

other

texts this

practice

is reversed.

9.4.7 The

equation of

impedance

It

is

necessary

to be able to calculate the

change in impedance

over the

length of a

pipeline.

Referring to Fig.

9.3,

atr

the oscillatory

head is

given

by

h'r: H, 9'*

and the

flow by

4'r=

Q*

Q'n'

where

FI,

is the amplitude of the head

oscillation

at r

and

Q,

is

the amplitude of the

corresponding

flow oscillation

at r.

e,o:

e,

er*:#

(s

e"'

-

b e-r')

Therefore

Adding equations

(9.22)

and

(9.23)

gives

2a:

Hs.#"eAs.

So

Resonance

h',:

e't>'

f+Hs-z"Q.r)

e" +

*(rls

+

Z"Q)

e-"'l

Sec.

9.5]

BoundarY

conditions

-

Zn*

Z.tanh(yL)

tt:@.

2L5

214

[ch.

e

Dividing

h',by

q'* gives

Z,:

F/5 cosh(yx)

-

Z"Q,

sinh(yx)

Q"

cosh(yx)

-

(HJZ.)

sinh(yx)

:

Hs- Z"Q, tanh(yx)

Qr-

(HJZ")

tanh(yx)

and

so

/_-

Zs- Z" tanh(p)

'

1-

(ZtlZ")

tanh(yr)'

At r:0, tanh(p)

also equals zero

and

the

above result

reduces

to a simple

equality

Zo: Zs

At

x:

L,

From

the

above

results

either

Z^can

be

obtained

in

terms

of'

Zs

or

Z, can

be

obtained

in

terms

of.

Z^.

9.5

BOUNDARYCONDITIONS

In

the same

way as

in

the analysis

of

waterhammer

by the

method

of

characteristics,

conditions

at

boundaries

control

the

magnitudes

of

impedances

throughout

the

network.

At

the

boundaries

the

conditions

present make

it

possible

to obtain

relationships

which

define

the impedance

at all

nodes

in the network-

9.5.1

Reservoirs

At a

reservoir

the

head

imposed

on

the

pipe is

rigidly

controlled

by the

depth

of

water

in the

reservoir.

The

piezometric

head

is equal

to the

height

of

the

reservoir

surface

above

the chosen

daium

minus

the

height

of

the centreline

of the

pipe above

the

r^+.,- 7 ^^,,^l- +t io Loinhf hrrr lrpnqrrce it ic rioirllv five.rl fhe valtre of h' must be

(laluttl.

t,

gqu4lD

llrlJ

rrwrSlrr

vulr

vvvssuv

rvrv-t

zero.

(In

some

circumstinces

this

is

not

perfectly

true. For

instance

waves

on

the

reservoir

can

be created

when

wind

blows

across

its surface

and,

in

fact,

pipeline

ruptures

have

been

caused

by

resonance

in

the

pipeline set

up

by such

waves.)

The

,uiio

h'lq'

at

a reservoir

is

thus

zero

irrespective

of the

value of

q'

.

Therefore

Zr"".rooir:0'

9.5.2

Blank

ends

It is

not

very common

for

pipelines to

have

branches

which are

sealed

off

by blank

ends

but

it ii

very commoo

for

valves in

pipe

networks

to be

closed.

The

pipe lengths

upstream

and

dbwnstream

of such

a closed

valve then

both

become

blank-ended

branches

in the

network.

At such

a

blank

end

there

can

be

no

flow;

so

both

q

and

q'

must

be zero.

The ratio

h'lq'

mast

always

be

infinite,

i.e.

Zbtankend:

@

'

9.5.3

Junctions

At

the ends

of

a

group

of

pipes which

join

at

a

junction

the

pressure

head

must

be

the

same at

all

the ends.-Also

ihe

flo*

that

comes

into

the

junction

must

be exactly

the

same

as

that

leaves;

this

last statement

is

merely

a statement

of

the

continuity

equation.

Then

2q,^:

)qo.*

and, as

f

is common

for

all

PiPe

ends,

:eQ'l--e1'*e-Tt

e'rx-e-Yr\

'\o"

,

-z,o't)

but

(er'

*

"-t*)12

--

cosh(Tr) and

(et'-

"-r')/2:

sinh(yt).

Therefore

h',=

"'*

[F/"

cosh(yx)

-

ft

sinh(yr)].

Similarly

Q5cosh(yx

)

-

|sinrr(yx))

.

zr: zn:

=

ztr=z=tanh\Yl)

,

1-

(zJZ")

tanh(yl)

Re-expressing

Zsin terms of. Z^by

manipulating

this

expression

gives

z,

Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

Подождите немного. Документ загружается.