Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

216

Sec.

9.51

Boundary conditions

z^r:

zrr.

A pipeline

consisting

of

a number

of

pipes connected

in series

is

merely

a number

of

pipistonnected

by

joints

and

so

are

very easily

dealt

with as

illustrated by

Fig' 9.6.

r

1-T

1

4-t

T

Z-/

z

1:1,277

Lin

i-l.m

Lout

(where

rz is the number

of

pipes

joining

at the

junction).

For

example consider a

four-way

junction

(see

Fig. 9.4).

@

Fig. 9.4

-

The four-way

junction.

Suppose that Zsr, Zsrand Z*rare

known

by calculation

from their other

end;

then

1111

-:

r-

J--

znr

znz'

zrr' z"r'

9.5.4

Joints

A

joint

is

merely

a two-way

junction

(Fig.

9.5).

So

Resonance

lch.

e

2r7

y

T'in-

T

Q'.,u,

.4 h' 4

h,',

i:l,m i:l.m

I

7

os,

le

S,

R,,

S,

Rr,

S,

R,

("nruoi,

o

@

o\

Fie. 9.6

-

A series

pipe.

ry

ct'(!t-

iqs)

2c3-

g{lA,

p3

and

0e

rta calculated

from

equations

(9.17)

and

(9.18);

so

Zca

can be

evaluated

from equation

(9.21):

We know

that

Z^r:

0 as

R, is

at a reservoir.

The characteristic

impedance

of

pipe

3

is

given by the

chaiacteristic

equation

(9.21)

requoted

here:

z

_

n

_

Zt^-

Z."tanh(TtLt)

oRt

1'

-

1

-

(zr!2.,) tanh(y3lr)'

So

Z\:

Z.rtanh(ytLt)

and

Zs^can

thus

be

evaluated.

Froh

the

boundary

condition

at the

joint,

Fig.9.5-Ajoint.

z^r: zs,

2r8

and

z

_

Z^.+ 2.. tanh(''{rLr)

os+-@

Again

Z^, Zrrby the

joint

rule and

so Zr,can

readily be

found.

9.5.5

Loops

In Fig. 9.7

a loop

is included. Loops (Fig.

9.8) are simple to

solve but,

when

two loops

and

7

-

Z^^*

Zotarfit(TtLt)

Lst-

t+

1z"1zr)

tanh(1.Lr)'

At

the

left-hand

junction,

2r9

Resonance

lch.

e

Z*,

/,sz

L

+-

'

zs,

reservorr

Fig.9.7.

Fig.

9.8

-

First-order

looping.

overlap

(Fig.

9.9),

a

problem

arises for which

the

author does

not know

the solution.

Fig.

9.9

-

Second-order looping.

He is

not

aware of any method of analysing

second-order

looped

networks.

In

Fig.

9.7,

ZRn= 0;

so Zso:

Z.^tanh(yoL).

At

the right-hand

junction,

111

-:-+-

zso z^r' Z^r'

2",+

Z",

t^"WtL)

zsr:@

A

further

equation

can

be

written

by

combining

the

two

junction

equations'

1

L_:

1

_

1

*

I

_

1

.

4,-

zr,-

2*,'

zr,

z^,

There

are

eight

equations

and

eight

unknowns

Zr,,

Z^r,

Zs"

Znr.'

1fr:

Z^r'Zsnand

i^,ifithe

pioble-

ir

no*

simflJto

solve

as

the

e{uatidns

aie

nol

all

simultaneous'

9.6

hTETWORKS

Networks

are

made

up

of

such

components

as have

just

been

described

but

other

boundary

conditionr

&irt

which

migiht

be

of

interest.

For

example

a

pump

might

be

included

in

a

network.

usually

pumis

are

not

generators

of

pressure

vibrations,

but

the

author

has

encountered-

i

pump

which

shed

vortices

at

its

cut

water

and

*o*qo"rrtly

vibrated

so

badly

that

it

caused

its

adjacent

pipework

to

fail'

A

in

a resonance

analysis.

This

is

because

the

m

oscillatory

component-

However,

if

a

in

its

flow

or

head,

it

can

be

dealt

with

by

e

realized

that

the

relationship

between

'Fl

Le relationship

is

parabolic

and

in

axial

flow

ationships

can

be

linearized

and,

in

some

r satisfaCtory

simulation

of

resonance

to

be

possible.

The

process

of

analysing

a

network

is

undertaken

by

starting

at

a

downstream

boundary

condition,

which

ils

usually

easily

specified,

and

working

upstream

evaluat-

ing

the

impedance

until

a

junction

is

encountered.

At this

point

it

is

necessary

to

220

Resonance

'[ch.

e

work

out

the

impedance

at every

other

branch

of

this

junction

and

using

this

information

to

obtain

the

impedance

at

the

upstream

side

of the

junction.

The

process

rnust

then

be

continued,

proceeding

upstream,

dealing

with any

junction

Lncountered

as indicated

above,

until

the

point at

which

the impedance

is

required

is

encounteiecl.

FreQuently,

thiS

pointis

at

an

upstream

point,because

in

the

process of

carrying

out

the

analysis

for

such

a

point it

is necessary

to obtain

the

impedance

for

all

nodis

in the

network.

In

effect,

this

technique

obtains

the

impedance

values

for

all

points

that

could

be of

interest

throughout

the

network-

9.7

ANATYS$

The

result

obtained

foI!"

impedance

is simply

a complex

number.

It takes

the

form

of.

a*ib

where

i:\/

1.

However,

a and

b

contain

constituent

variables

which

inciucie

O, the

angular

velocity

of

the frequency,

and,

as

f,)

increases

from small

values

to

large

nal,res,

the

value of.

Z

will alter

in

a most

complex

and

non-linear

manner.

It is

not

unusual

for

the

analysis

to

be started

at

a

C)

value of

0.01

and

to

^-r^,,tqra ,rqtrrpc nl T fnr inr-rernenfs in O of O 01 The nrocess is then continued

until

a

vctlvurqlv

Yqluvo

vL

u \vt

--

- ---

r-

frequency

is

reached

which

is

considered

to

be so

high

that

the

analysis

can,

safely,

be

disiontinued.

The

result

of

doing

this

can

be

plotted in

the

form

of

a diagram

such

as

Fig.

9.10.

From

this

diagram

the

risk

that

the

network

becomes

resonant

can

be easily

--/

Fig.

10

-

The

harmonic

diagram.

assessed.

The

peaks

on

the

harmonic

curve

specify

the

resonance

frequencies.

The

magnitude

of

the

resonant

pressure

heads

can

be calculated

if

the amplitude

of

the

forJing

frequency

causing

the

resonance

can be

specified.

Even

if this

is

not

possible,

it

is obvioui

that

it

is

vital

to avoid

the

generation of

the

frequencies

corresponding

to

such

peaks.

9.E

FORCINGOSCILLATIONS

The

methods

advanced

in

the

preceding

paragraphs

are

capable

of

predicting

the-

frequencies

at

which

resonance

occurs

but

do

not

give

any

idea

of

the

magnitudes

of

the oscillations

as

yet.

The

techniques

already

developed

are

quite

capable

of

Forcing

oscillations

22r

Sec.9.8l

encornpassing

this

requirement..

Assume

that

a

forcing

oscillation

is

present

uprtr"itn

for

which

the

equation

is

h'o:

Ho

rgt*

and

FIs

-

Ho'

zswlllhave

already

been

evaluated

in

the

impedance

analysis

andwill

be

a complex

number;

so

H"

er:_ir.

Therefore

Q,

will

now

be

known'

again

as

a

complex

number'

AtaPointxdownstream'

h'x:"t*

[Ilt

cosh(1x)

-

Z'Q'

sinh(1x)]'

So

H,:

Hs

cosh(Yx)

-

Z"Qt

sinh(Yx)

and

similarlY

Q,

:

Q scosh(1x)

-

H-t4sinh(1x)'

the

cause

of

resonance

as

have

servo-con'

circumstan"",

io

*hich

Bernoulli's

equation

and

continuity

can

be

used'

Generally,

flow

through

un

orin.J

is

governed

by

an

unusually

simple

equation

7t

,\

It

tt

/\

q:

a"!28h

222

Resonance

lch.

e

where a. is

the'effective'area of the orifice

and

equals Caao

and

Co

is the coefficient

if

discharge

of

the open area of the

valve; a

valve,

then, is an example of an orifice

obstructing

the flow.

An

alternative

way of writing this equation

is

,

Kqz

rl:3

/84.'

where K is

a number

which ranges from small numbers

for a wide open

valve

to

very

large numbers

for

very

nearly closed

valves

and up to infinity for

fully closed

valves.

9.9 TIIE

TRANSFER

MATRX METHOD

The

inventor

of

this method is

Hanif

Chaudhury

who took a

technique from

structural

analysis

where it is used to analyse

vibrating

structures

and applied

it to the

analysis

of

resonant

pipe

networks. It

is completely

explained

in his book

Applied

hydraulic

traruicnts.In

essence,

the

same equations

as

were

used

in the hydraulic

impedance

method

are used, along

with

the same boundary

conditions.

The

equations

applicable to

each

pipe

together

with the boundary conditions

are

written

in

matrix form

which can then

be

solved

quite

straightforwardly.

This technique is

much better suited

to the solution

of loops

than

is the

hydraulic impedance method.

9.10

TIIE

FOTJRIER

ANALYSIS METHOD

This method

was

suggested

to

the author by Professor A.

E. Vardy. It

is very

simple

indeed. It requires

that

the user has

available a complete and detailed

characteristics

program. A wave

generated

by a

step

in

flow

amplitude

is applied

to the

prototype

network

which

is under

analysis. The smallest Ar

that the size

of the computer

random-access

memory

permits

and the

longest

possible

time of simulation

are used

in the analysis.

The

resulting

wave is then subjected

to

Fourier analysis.

The

Fourier

analysis

will

yield

all

the frequencies

which

could

produce

resonance

up to

the

harmonic the semi-wavelength

of

which

is

equal to

the A.r length. This and

any

higher

harmonics

cannot

be

regarded

as real. Individual resonant frequencies

can then

be

analysed by

the characteristic

program

employing all the frequencies

established

from

the step

analysis

in turn.

10

Three-dimensional

free

surface

flow

rO.1

INTRODUCTION

In

previous chapters

the

theory

of

unsteady

flow

in open

channels

has been

presented

and

discussed.

The

theory

Ldvanced

is

two-dimensional

and,

strictly,

is only

applicable

to channels

in

which

the

assumption

can

be

made

that

the depth

across

the

cioss-section

can

be

regarded

as

approximately

uniform

and

that

no

transverse

components

of

the

vetoiity

are

generated.

In fact,

the

theory

is often

applied

to-

channels

of

circular

or

traplzoidal

cross-section

and

this

does

not

generate

errors

of

significance.

It

is true

thatiecondary

flow

effects

are

created

in

such channels

but

this

is

also

true

of

channels

of rectangular

cross-section

in

which

the

depth

is

perfectly

uniform.

In rivers,

estuaries

andsuch

channels,

cross-sections

can

exist

in

which

these

assumptions

are

not

even

approximately

true;

in

such

channels,

secondary

flows

are

an order

of

magnitude

stronger

than

those

that

occur

in

channels

that

can

be

treated

by

one-dimensi-onal

"pptoa-hes.

In

the

same

way

that

two-dimensional

channel

flbw

@ig.

10.1)

can

be

analysed

by

finite

difference

methods

and

also

by the

Fig.

10.1

-

One-dimensional

channel'

method

of

characteristics,

three-dimensional

flows

(Fig. 10.2)

can

be

analysed

by

finite

difference

methods

and

by the

theory

of

bi-characteristics'

IO.2

THE

THEORY

OF

BI-CHARACTERISTICS

This

theory

is often

said

to be

a three-dimensional

theory

and

this

is

correct

in

that

two

dimenrion,

of

distance

and

one

of

time

are

involved.

In

fact

the

problem

is really

224

Three-dimensional

free surface flow

lch.

10

Fig. 10.2

-

Three-dimensional

channel.

a four-dimensional

problem:

three

of distance

-

length, breadth and depth

-

and

time.

The only current

method

of

which

the author

is cognisant,

which

can handle

four

dimensions,

is by integrating the

Navier-Stokes

equations

and

this can only be

sensibly

attempted

on a supercomputer.

At the time of

writing,

much

work

about

parallel

programming

is

proceeding

and most

of

it is concerned with integrating

equations

of a type similar

to theNavier-Stokes

equations.

This work

cannot be

regarded, as

yet,

as usable for the routine

solution of

problems

of the type described

in

this book but it

will

certainly become

possible

to

solve

the

Navier-Stokes

equations

in the future

using

very

high

speed computers. Almost certainly, it will

always

be time consuming

to

solve the Navier-Stokes

equations; so the bi-character-

istic

method

will remain useful for the

solution of shallow

water,

long

wave

problems.

The bi-characteristic

method

is not,

currently,

as

popular

as finite

difference methods.

Much

work

has been done

on the method but because of its

greater

complexity it is

not

extensively used. It has one

great

advantage:

it is

inherently stable

whereas finite difference methods

are not.

In the theory of

the bi-characteristic method

it is assumed that velocities do not

vary

with depth,

i.e. in

the

z direction but do

vary

in the r and

y

directions. This

constancy of

velocity with depth neglects the

effect of the boundary

layer created

by

bed friction but this

is taken into account

separately by the inclusion

of

a friction term

in the

momentum equation in

a way

identical

with

that

used

in the one-dimensional

approaches

already

described.

The

Euler

equations

are well known

and describe the relationships

between the

pressure gradients,

momentum rates of change

and the

forces

acting on a fluid

element.

They

neglect frictional forces. They

are

statements of

Newton's

second

Law.

+*x:r("*+,X****#)

,

-An

/

Ou Ou

Ou Ou\

6

*

Y:

o

(,;

* ,6 *,;*-u,)

,

The

theory

of

Bi'characteristics

225

Sec.

10.21

-op

+z

/

Ow

.

ow

dw\

dz

i-

o(r;*ray

*n$*a)

If these

equations

are

applied

to

a

free

surface

flow

and

the

r

and

y

directions

are

chosen

perpendicular

to

one

another

and

parallel

tothe

channel

bed

then

the

body

forces

X

and

Y

are

-

pgi,and

-

pgi, respectively

where

i' is

the

bed slope

in

the

'r

direction

and

i,

is

the

u""Aitop"

in

itre

y

dir-ection.

Here.the

mathematical

convention

is being

used,

i.r.

tftui

the

slope

i in

tire

first

quadrant

is

positive'

It is

more

usual

to

,rgurd",

slope

in

the

fourth

quadrant

as

positive

in

the-special

caseof

open

channels

and

the

convention

is

now

a;cepted

thai

a channel

which

slopes

downwards

in

the

downstream

direction

is

a

positive

slope;

so

the

body

forces

Xand

Y are

pgi,and

pgi,

respectively,

the

signs

being

,"n"rted.

In

the

z

direction

the

body

force

Z

is

-

p8'

The

negative

sign

iJintroAuced

here

because

Zistheweight

Pg

ger

unit

volume

and

acts

downwards

in

the

direction

of

z

decreasing.

The

assumption

ismade

that

there

is

no

velocity

in

the

z

direction;

so,

everywhere,

w is

zero

and

all

its

derivatives

in

both

spatial

and

time

dimensions

are

also

zero'

It

therefore

follows

that

opldz

:

-

p8

and

so

integrating

with

respect

to

z

between

the

limits

of

zero

and

t'he

depth

d

gives the

result

thatplw:

d; thus

dpldx

-

ipAarl.This

is

a

well-kno*o

,.rrrlt

Uuiit

totally

depends

{or-itl

validity

on

the

assumption

that

there

is

no

component

of

velocity

in

the

vertical

direction.

It

then

also

follows

that

tt

"

pt"ttore

is

hydrostatically

distributed

with

depth'

This

circum-

stance

is

closely

appioximated

in

many

free

surface

flows

such

as

open

channels,

rivers

and

estuariis.

fne

hydrostatic

issumption

rarely

applies

to

waves

in

deep

water;

so

the

theory

is

commonly

called

shallow

water

wave

theory'

A consequence

of

the

assumption

of

frictionless

flow

is

that

the

values

of

z

and

u are

constant

with

depth

so

they

can

be

regarded

as

mean

values.

Taking

account

of

atl

the

foregoing

the

Euler

equations

reduce

to

-"X-'(,#

-,X

#)

twi,=0,

-*X-'(,#-,#

*)

*wi,:o

(10.1)

(10.2)

w in

eqns

1.0.1

and

10.2

now

represents

the

specific

weight

o-f

the

!Yid'

It

is

now

n"."rr"ry

to

take

account

of

friction.

The

assumption

that

the

flow

is frictionless

was

essential

to

the development

of

the

above

equations

and

for

them

to

be

valid

the

flow

must

be

regarded

as

inviscid

with

no

inigrn-al

shears

in

the

body

of

the

fluid'

Flowever,

it

is

possible

to

concentrate

all

the

omitted

frictional

effects

at

the

boundaries.

Thus

the

behaviour

of

the

flow

will

be

correctly

modelled€ven

though

the

internal

behaviour

will

not

be

correctly

described.

Rewriting

the

Euler

equations

226

Three-dimensional

free surface flow

lch.

10

Ad udu uOa

0u rx.

.

n

-a'-;t-Eay-

u-;+tr:u

'

Ad u)o udu

0u r

-;--

--'-Y*i":Q

Ey

gOx g}y

0r

w

'

Multiplying

through

by

-

I

gives

Ad u)u u)u

0u r-

ar+;t*tay*

u*i-L:u

and

Ad uOu u

0u

r..

-T

Ox

g1x

g}y

0t' w

where

t, and ry are the bed shears

acting in the

-x

and

-y

directions respectively.

The

term

rlw equal@ uzlc2dwhich in

turn is equal to7, which

is the energy lost

per

unit weight

of fluid

per

unit distance

down the slope in

the r direction.

Simitarty

y'w

u2

is equal

to

Czdwhich

equalsy".

A

third equation is available and this

is the equation

of conservation

of

mass.

Given

that the fluid can

be considered

to be incompressible

this

is

-0u

Ad

.0u

Ad Ad

d-* u-*

d-* u-*::0

ox

dx dy

oy or

This

equation can

be

simply obtained by

considering

a

vertical

rectangular

volume

of dimensions 6.r in the .r direction,

6y in the

y

direction

and dz in

the

z

direction.

The

equation

comes from the

consideration

of the balance

of

inflow and

outflow

into and

out

of this

volume

in a

short

time

0t and the

equating of

this

amount

of

volume

to the

volume

traced out by

the

water

surface in this time.

The

equations then are

Ad uOu

u)u

0u

-

+__+:__-

+i

_L:0

,

Ox'

gOx' g}y'

61

'"

Ad uOv uOu du

u-*;''*rt*t

+iv-i":o

,

-0u

Ad

.0u

Ad Ad

d-*u-*d-*u-*::U

dx dx oy

oy dt

Sec.

10.31

The

characteristic

equations

of

three-dimensional

flow

r0.3

THE

CHARACTERISTIC

EQUATIONS

OF

THREE-DIMENSIONAL

FLOW

The

characteristic

equation

is

lUcos0

+ usin0

+2c)-

E

cos

g

+ Evsin0

:

Dtt

where

DtDtis

the

differential

operator

defined

as

follows;

-'

[sin'eff

-

sine*,t

(#.

#)

+

.",'o#]

227

(10.3)

(10.4)

Daa^

W:

At+

(u+ccos0)*

*

(,

*

csinel

ay

The

angle

0

can

take

any

value

between

zero

and

Zn.For

each

value

of

0

the

equation

describes

the

conditions

that

occur

along

a

characteristic

line

in

time

and

space

the

direction

of

which

is

defined

by

the

two

following

relationships:

fl:r*csin0

,

$:r*ccos0

Equation

(10.3)

is

called

the

compatibility

equation

and

applies

along

the

character-

istic

definio

uy

equations

(10.4).

Ttreri

aie

close

resemblances

to

the

concepts

described

when

the

theory'of

ciraracteristics

of

one-dimensional

flow

was

being

discussed

earlier

in

this

book.

'ion

(L0.4)

are

statements

that

a

wave

ave

a

velocity

in

the

y

direction

due

to

the

:

celerity

c in

the

y

direction'

Similarly

the

on

will

be

caused

by the

two

components

a

rn.

This

leads

to

Fig.

10.3.

consider

a circle

of

radius

c

dt on

the

x-y

plane

at

time

level

t.

From

each

point

on

the

circle,

a

characteristic

line

travels

up

the

surface

of

the

conoid;

these

meet

at

the

"p..

"t

,fie

conoid,

which

will

be at

a

point

displaced

from

the

centre

of

the

circle

by

distances

of

udt

and

udf

on

the

t+ it

plane

where

u and

u

are

the

mean

velocity

components

in

the

r

and

y

directions

o'

contlqn"nce

of

the

two

equations

defined

joining

the

centre

of

the

circle

to

the

apt

diff"tJftom

a

characteristic

line

which

is

path.

All

characteriStics,

of

which

there

are

an

lnhnlte

numDer'

meet

at

LUt;

aPeJa

au\r

continue

upwards

in

the

x-y-t

space.

The

volume

enclosed

by

these

continued

characteristics

can

be

thought

of

as

describing

a

point in

space

at

timeJ

*

dt'

i'e'

at

the

apex

of

the

original

conoid

from

which

is-emitted

a disturbance

which

radiates

228

lch.

10

circular wave is transported

in the

r andy directions

at

velocities

u and u. This

causes

the

conoid

to be skewed and,

if the

velocities

rz

and u vary

as time

passes,

the

conoid

will

also

be twisted.

The shape

is thus

a skewed twisted

conoid. If u and u

can be

assumed

to be

constant

over

the

duration

of one dt,

the conoid

can be regarded

as

skewed

and the twisting

effect can be neglected.

This last

assumption

is equivalent

to

the assumption

made in

one-dimensional

theory

that the

short lengths

of the

characteristics

in the solution

triangles can

be regarded

as

straight. If the

conoid

apex

lies

outside the

origin circle in the.r-y

space, the

flow is

supercritical

and

when

it lies

within

the

circle the flow is subcritical.

The

circular

area in the

x-y space at

time f

is

the domain

of dependence

of the apex

P and the

divergent

sheaf of characteristic

lines

arising from P defines

an enclosed volume

which

is the range

of influence

of P.

The

volumes

outside the conoid

are known

as

the domain

of determinacy.

The

square formed

by

the

spatial nodes which

contain

the circular

domain of dependence

is known

as the dsrnnin

of finite difference.

When

integrating

up the characteristic

lines,

interpolations

for

values

at

their bases

can

only be

successfully

performed

if the

circular

domain of dependence

is totally

enclosed

by this

domain

of

finite difference.

10.4

TIIE

INTEGRATION

OF

TI|E

CHARACTERISTIC

EQUATIONS

There

are an infinite number of

characteristic

lines

in

the conoid;

so

an

infinite

number

of equations can be

written

all

of

which

are

equally

valid.

It is

obvious that,

when

an infinite number

of equations

are

used,

a situation

equivalent to an

integration

around

the base of the

conoid

is being

undertaken.

This concept was

investigated

by

A.

E.

Vardy

at Dundee

University.

C-onsidering any

point

on the

circumference

of the

base circle, equations

for the velocities

u andu and the celerity

c

can

be

written

using linear interpolations

between

appropriate values

at adjacent

node

points.

Finite

difference forms

of the characteristic

equations can be written

using

these

equations for

the base

values

and

these,

together

with the

particle path

line

-

derived

from the

continuity equation

-

gives

the

c

value

at

the t +

dt level.

Sec.

10.41

The

integration

of

the

characteristic

equations

229

Using

this

value,

back

substitution

gives

the

u and

u

values

at

the

t

+ dr

level'

This

method

has

not

been

employed

in

many

applications;

so

little

can

be said

about

its

suitability

for

general

use-

10.4.1

The

four-Point

method

The

method

described

above

can

be

demonstrated

by

using

a four-point

method'

This

method

has

some

peculiar

advantages

and

some

disadvantages'

The

conoid

is

illustrated

in

Fig.

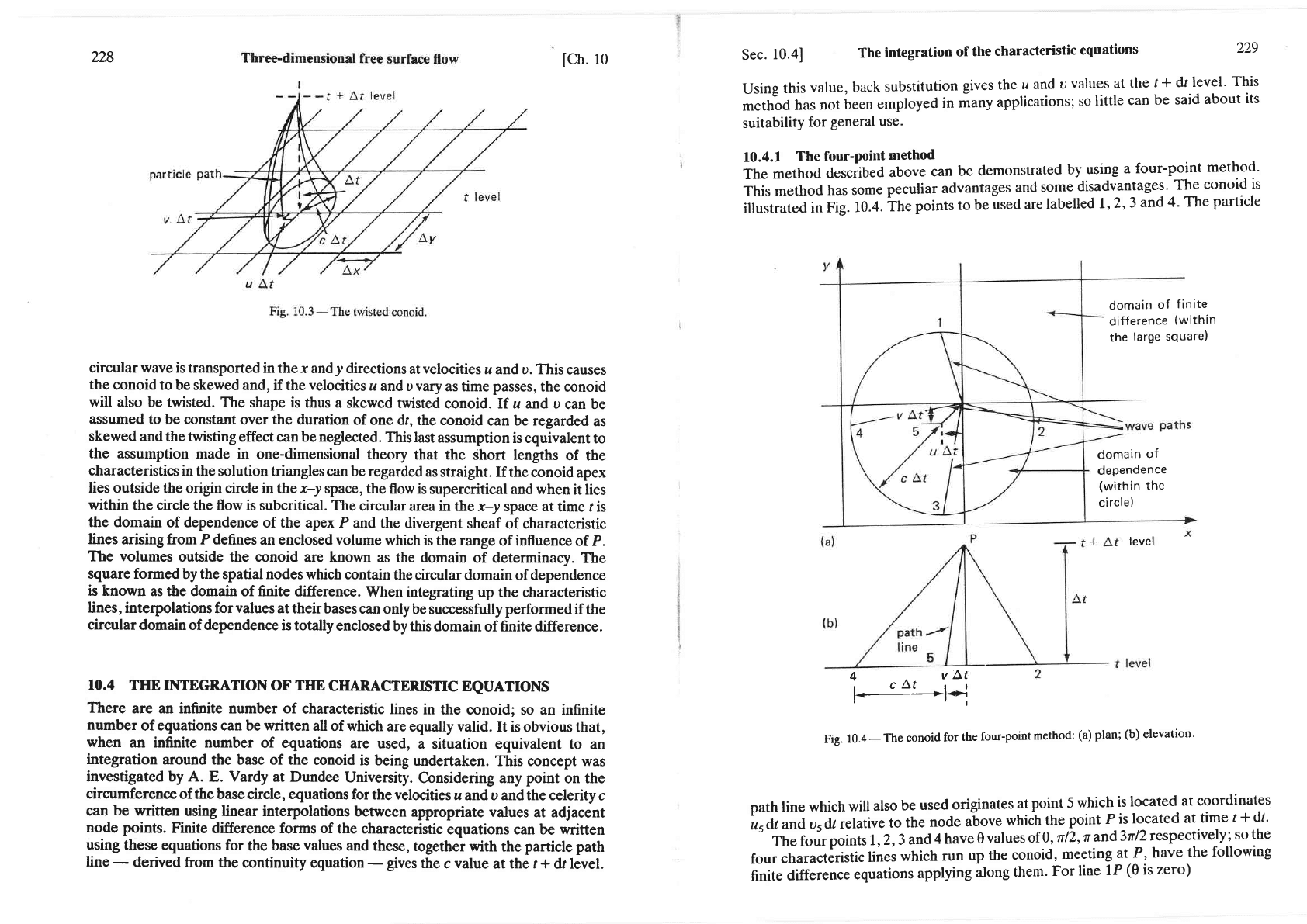
10.4.

The

points

to be

used

are

labelled

1,2,3

and

4'

The

particle

level

4 vA,t

,

cAt

I

r

I-.---------.--------_ff

Fig.10.4_Theconoidforthefour-pointmethod:(a)plan;(b)elevation.

path tine

which

will

also

be

used

originates

at

point 5

which

is

located

at

coordinates

Lrdt

andu,

dt

relative

to

the

node

u-bon"

which

the

point

P

is

located

at

time

t

+ dt'

ThefoJrpointsl,2,3and4have0values

of.O,nlL,rand3rlZrespectively;sothe

four

characteristic

lines

which

run

up

the

conoid,

meeting

at

P,

have

the

following

finite

difference

equations

applying

ilong

them.

For

line

1P

(0

is

zero)

domain

of

finite

difference

(within

the

large

square)

domain

of

dependence

(within

the

circle)

230 Three-dimensional

free

surface

fl

ow

lch.

10

(10.sa)

(10.sb)

(10.sc)

(10.sd)

Along

the

particle path

line dx/dt:

u

and dyldt

:

o.

Use

the

definition

of

the

total derivative

of the wave

speed c with

respect to

time:

uo*2cr-

th-Zcr-

ElLt=

For

line

2P

(g

is n/2),

ur*Zco

-

t)2-Zcr* ErAt:

-

cp

For

line 3P

(0

is n),

0c

_:

0t

-

uo *

2co

*

u,

-

Zcr+

E3Lt:

-

rr/'

O,

For

line

4P

(0

is 3nl2),

-

up*bo*

uo-2co-

EoLt-

-

cp*U,

The

continuity equation

given

earlier

is

Ad

Ad Ad

.0u -0u

ar+ua**"r*ox*our:o

for d. This

reduces

to

0c

0c tdu

10u

u+

"

a**'t,

*rx*rw=u

This

gives

*o,

dx

Dc

0c

.

Ocd-r

.

Ocdy

-:_J-__J___

Dr

0t 0x dr

0y dr

I

oc

oc lou

1

ou\

-

\'a,

*'r,

*lu*zut)

Sec.

10.51

Boundary

conditions

In

the

equation

for

the

total

derivative

of

c

with

respect

to

f

given

above

,

replace

dxldt

by

z

and

dyldt

bY

u.

Then

Substituting

for

0cl0t

into

this

expression

glves

(10.6)

231,

Dc

0c

w:

u+

"

ar*'ay

Dco:3(%*9.%\

Dt

2

\0t

AYI

By

adding

and

subtracting

equations

(10.5)f uo.and

De

can

be

eliminated

and

an

eipressioi

in

co

and

@ulai+

iuay)ocan

be

obtained.

These

expressions

can

then

be

co

mbi

ne

d

* ittr

e

qu

uii o

n

(

1

0

-

6

)

te afr

n

g

*TJil

lili"9.ii

J;;

?,T*'tl;il:fi

il

JH:

but

it suffers

from

a

disadvantage

in

that

. at

multiples

of 90o

are

not

detected

until

polation

rectangles

and

have

traversed

worth

while

to

develop

rnethods

employ-

ing

more

interpolation

points

and

correspondingly

more

compatibility

equations

so

that

the

analytic

method

becomes

more

sensitive

to

waves

arriving

from

other

angles

'

If it

is

wished

to

use

large

At

values

to

reduce

the

number

of

time

levels

to

be

handled,

it

will

be

necessuty

tJ

perform

the

twisted

conoid

analysis

and

this

will

involve

second-order

tech;ques^which

will

offset

much

of

the

gain in

speed

achieved

by

the

use

of

large

At

values'

It

is

obvious

that

waves

approaching

in

an

x or

y direction

affect

interpolations

by

altering

values

at

three

nodeJbut

wavis

advancing

in

other

directions

initially

only

affect

a single

node

(Fig- 10-5).

Itwould

therefore

seem

desirable

to

use

a

multi-point

methodinwhich

more

than

four

points

were

involved.

Many

such

techniques

have

been

evolved

and

the

reader

is

referred

to the

specialist

literature

for

details

of

them.

The

method

described

is,

to

a large

degree,

first

order

and

so

can

only

deal

with

a

skew

conoid.

To

handle

the

twistedikewionoid

requires

second-order

techniques'

ttre

price of

such

methods

is

high

in

that

computing

time,

whiclr

is

already

large,

becomes

two

or

three

times

larger.

There

is

a

large,

highly

specialized

literature

on

the

subject

and

the

reader

is

recommended

to

coniult

this

to

increase

his

background

in

this

comPlex

field.

10.5

BOUNDARYCONDITIONS

The

plan of

the

flow

channel

must

be

first

examined

to

decide

how

its

boundaries

are

to

be

represented

(Fig. 10.6).

short

lengths

of

any

of

the

boundaries

have

to

be

represented

by

on.

br

6tn",

oi

the

sides

of-a

mesh

of

the

grid.

If

the

Tgth

is small

and

the

grid rorr"rpondingty

fine,

the

representation

will clbsely

resemble

the

shape

of

Finite

difference

methods

233

232 Three-dimensional

free surface

flow

lch.

10

Fig. 10-5

-

Detection of

waves

moving in

directions

other than

an r or

y

direction.

Fig. 10.6

-

Modelling of

a flow

channel.

the channel but

the analysis

will

involve

a large run

time.

Conversely, a course

grid

will

provide

a

poor

representation

of the flow

channel

but the

analysis

will

require

much less

run time.

The boundaries will

run

either in

anx

direction or in ay direction.

The required

condition at a boundary

is that

the flow velocity perpendicular

to it

must

be

zero. No friction from

the

side of the

channel

can be included in

this type

of

analysis

but an approximation to it

can

be obtained

by

suitably increasing

the bed

friction in

the adjacent

grid

mesh.

Otherconditions

can be modelled

by

similar

methods

as were

given

in

ChapterT.

10.6

FINITE

DIFFERENCE

METHODS

As

with

two-dimensional

methods

described

in

the

it

is

possib_le

to

integrate

the

basic

equations

of

three-dimensional

flow

directly

using

similar

finite

difference

methods,

The

process

is

much

simpler

and

quickgr

lhal

the.

bi-characteristic

method

iust

described

but,

like

all

finite

diff"t"n."

methods,

it is

liable

to

suffer

from

instability

and/or

diffusion

error.

The

simplest

representation

of

a finite

difference

can

be

used

and

substituted

in

fhce

of

the

purti"t dirivatives

in

the

basic

equations-

This

will

give

solutions

for

the',

*-pon"nt,

th"

u

component

and

the

depth

d'

This

simple

technique

has

been

successfully

employed

but

the

author

would

not

like

to offer

any

guarattlee

of

its

resistance

to

instability'

Sec.

10.61

Sec.

11.21

Basic

equations

So

235

(1

1.1)

(1r.2)

tl

Transient

flow

in

gas

pipe

networks

1I.1 INTRODUCTION

The

techniques

of

analysing gas

flows

are

not

identical

with

those

used

for

liquid

flows

although

there

are

considerable

similarities

between

the

equations.

the

essential

difference

between

them

lies

in the

much greater

compressibility

of

gas

when

compared

with

liquids.

tt.z

BASIC

EQUATTONS

ll.2.l

The

continuify

equation

The

rate

of increase

in

the

mass

of an

element

of

gas

of length

Ar

equals

the

difference

between

the

rates

of

entry

of

gas

to

the

element

and

exit

of

gas

-from

the

element.

So

a

abo6-r)

-

Therefore

g*rort

+${oa,):o

Thus

In

pipelines,

pressure

fluctuations

are

not

sufficiently

large

to

cause

pipe

distensions

when

comparedwittr

ttre

compressibility

of

the

gas.OAtOtcan

be

ignored

and

omitted

from

the equation.

The

continuity

equation

therefore

reduces

to:

*.|X*,ff.N#*o*=o

*.,$*o#*

T#:o

11.2.2

The

dYnamic

equation

By

applying

Newton's

second

law

of

motion

to

an element

of

gas

of

length

6x'

the

net

force

^u"tin!

in

the

direction

of

flow

(i.e. in

the

direction

of

r

increasing)

equals

the

rate

of change

in

momentum

of

the

element:

-WDe-.,-OA"-

,

d'

a*r&+pi6x-F6r:PA6rA'

The

second

termp(o

Abxlox)is

the

longitudinal

force_acting

upon

the

element

due

to

the

increment

in

area

in

the

longitudirial

direction.

F is

the

frictional

force

per

unit

length

acting

upon

the

element

and

opposing

the

flow-

This

reduces

to

*.

e,#*

p* *!o:o

-

(*(pAu)&)

11.2.3

The

equation

of

statc

of

the

gas

sary

to

involve

any

equation

of

state

of

the

rt

pressure

changes

cause

no

change

in

eal

is

so

large.

This

is

not

true

for

gases

hanges

of

density

and

temperature'

For

a

perfect

gas the

internal

energy

per

unit

mass

is

e:

CvT:Ai

where

C'

is the

specific

heat

at

constant

volume

and

T

is the

absolute

temperature'

Also

1ff

*pX*e,ff*p,#*aoff:o

Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

Подождите немного. Документ загружается.