Fox J.A. Transient Flow In Pipes, Open Channels And Sewers
Подождите немного. Документ загружается.


116
Boundary
conditions
lch.
4
where A, is
the
plan
area
of
the
liquid surface
and
h,is
the depth
of
the
liquid
in
the
tank. The
wave
path RP,
is
the characteristic
line
running
through
the
upstream
6x
which connects
with the
downstream
wave
path SP2
in
the downstream
Ax. Note
that
the
points P,
and
P, cannot
be considered
coincident
because
the
velocities
ul(i,
netno(i))
and u1(i
+ 1,
1)
do not
have the same
value
even
though
they
have
the
same
head.
The
Reimann
invariants
for these
two
lines
give the equations
+
3-
(h",- h*)+
Dp,
-
rrn *
'&*&
:
o
and
-L(hrr-
hr)+
t)pz-
u"*'#:o
-
Now
hr,is equal
to
hrrand
these
two
heads
are
made
up
of
the
following
constituents':
the
height
of
th"e
j
unction
of
the
tank with
the
pipe
,
i. e.
z1
above
datum,
the elevationhr,of
the
base
of
the tank
above
the
junction,
the
height
/rrof the
water
surface
above
the base
of
the
tank
and,
finally,
the
pressure
head
in terms
of
the
liquid
column
height equivalent
to
the
pressure
p.,,
of
the
air in the
tank.
Because
all
caiculations
of
the
fluctuating
air
pressure in the
tank
must be
made
in terms
of
pressures referred
to
vacuum,
i.e.
absolute
pressure, the heads
in
the
network
are
all
ibsolute
also.
In the case
of
a network
which does not
contain
an
air
vessel
this
requirement
does
not have
to be
observed
but
the wisest
course
is
to
assume
that,
some
time
or other,
the solution
program will
have to
deal
with a
network
which
includes
an
air
vessel and
to
use
absolute
heads
and
not
gauge
heads.
I-et
the
initial depth
of
the
water
in the
air
vessel be
hr and
the
pressure head
in
the
tank
be
/r*.. Then
the
initial
heads
in the
pipes
joining
ai the
base
of
the tank
will
be
hr,
hp2:
Zr+
hr+
ht.+ h*.
.
The
initial
values
of
hr,andhr,will
be defined
by the initial
conditions
of
the network
and, as far
as
the air
vbssel
is concerned,
can
be regarded
as
determined.
Then the
initial
pressure
head
of
the
air
in the
vessel must
be
fu*r:
hp,
Z,
-
h,
-
futi
Let
the
depth
of
water in
the
vessel
at time
tbe hr;then
this
depth at
time
r
* Ar
will be
Sec.
4.131
but
The analysis of
air
vessels
oft
_
A(i) u1(t,
netno(t))
-.4(t
+ 1) ul(t
+ 1, 1)
0r
Ar
and, as all the
variables
on
the
right-hand side
of this expression
are known,
hrfor
time
r * A/ can be
calculated.
This change
in h, involves
a
change
in ft*
(the
pressure
of
the air expressed
in terms of
head of
tiquid). The change
can be calculated
using
the equation of
the
isentropic
process.
It has
been common
pracdce
in the
past
to use
a
polytropic
process
but recently
evidence
has
been accumulating
that the
process
in
an air
vessel
is better
approximated
by an isentropic
process. In fact the
process
is not
well described by the
polytropic
process
and
not
very well described
by the isentropic
process
either.
In
fact the correct
analysis
that should
be used
is the full
thermodyna-
mic treatment.
This could
be done
but it may
be difficult
to obtain
some
of the
constants
that would
be required
for this
treatment.
The isentropic
process
is
So
PnVr:
k
because
V
:
Llp
where Vis
defined
as being the
volume
occupied
by
a
unit
mass of
gas.
Assume that
there
are m
units of
mass in the
vessel
and this
will
not change
throughout the
air
vessel's
period of operation.
If It
is the length
of the
vessel and h,
is the depth of
liquid in
the tank
(tr
o
is the depth
of
water in the
tank at the
initial time
l,) then
p*
:e,
(
h-hr\'
p*,-
Art\I^-
h,
)
For a
vertical
cylinder
At is constant
and
p*
:
ft*,w. So
h*
_(
rr-nrlt
-=
|
-
h*i
\Lr-
hhl
Thus hn canbe calculated.
This
will
give
the
pressure
head
of the
air
at time
r + Ar
expressed
in metres
of liquid.
Then
rL7
fu:k
pl
hr*or:
h.+*O'
Hpt:
hpz:
Z + hT
+
h+
h*

118
Boundarv
conditions
lch.4
Next
use
the
wave equations
to
give
the
values of
v", and
v
r,
fi{nr,-
h^)+
vP, ,^ *@j9:
o
where
d,
denotes
the
diameter
of
the ith
pipe.
So
DP,
:
DR
-
f^{nr,-
h^)
-zf
^'4:A
nt
'
Similarly
the negative
characteristic
in
pipe number
i * 1
gives
-L(hrr-
hr)
+ t)pz-
us *
'#:o
So
o )f
u"lu"l Ar
Dpr:
nr+
zr(hrr-
h")
This
process
will
give
the
pressure
history
at
the
pipe
junction,the
velocities
at
the
junction
and the
level history
in
the tank together
with the
air
pressure in
the
tank
over
as long a
period
of
tirne as
may be
required.
4.13.2
The horizontal
cylinder
When the flow
in
the
pipeline
is
large, it may
be considered
to
be a sensible
idea
to
provide
a
large
surface
area
in the
vessel.
The cross-sectional
area
of
a
vertical
cylinder is
much smaller
than
the diametral
area of
a long
horizontal
cylinder
of
the
same
diameter;
so
the
use of such a cylinder
can be
attractiye.
It will
be
found
necessary
to use
multiple-entry
ports
to
such
a
cylinder,
otherwise
longitudinal
surface
waves may
develop
in
the cylinder;
and these
could
generate an
additional
wave system
overlying
the main system
of compressional
waves in the
network
(see
Fig.4.11).
The obvious
reason
for
using a horizontal
cylinder
is that,
when a
large
volume
of
air is required
to
provide the damping
effect
that
is required
to convert
the high
sharp
transient
oscillations
into
long
low mass
oscillations,
it may
prove
impossible
to
build
a
vertical
cylinder
of
the required
height.
The difference
between
the
analysis
of the
vertical
cylinder
and
the horizontal
cylinder
lies
in the
variability of
the
water
surface
area.
The
operating
level of
the horizontal
cylinder
should
be
at the
horizontal
diameter
or a little
below.
Then,
when the surface
rises, the
pressure rises
relatively
slowly
because
the air
volume is at, or
near,
its maximum
value. As
the
level
rises
Sec.
4.131
The analysis
of
air
vessels
119
XR
N,
N,
(a)
(b)
Fig.
4.11
-
(a)
The
horizontal
cylinder
and
(b)
its associated
r
versus
t diagram.
further,
the
volume
decreases
more
and
more
rapidly,
eventually
decreasing
more
rapidly
than
the
rate
at
which
the
volume
decreases
in
the
case
of
the
vertical
.yiinOlt.
The
pressure
rises
at
an increasing
rate,
decelerating
the
flow
more
and
,nor"
powerfuily.
The
horizontal
cylinder
is favoured
when
an air
vessel
has
to
be
fitted
to
a
very
long
pipeline.
Horizontai
cytinOtis
have
been
made
out
of sections
of
pipe
of
largediameter
and
it
is
easy
to
fit two
such
cylinders,
one
on
each
side
of
the
pipeline;
multiple
entries
to
the
cylinders
must
be
usld
to
prevent
the
generation
of
tongitudinal
waves
in
them.
The
cylinder
must
be construCted
so
that
it is as
perfectly horizontal
as
possible.
The
analysis
of
the
air
vessel is
the
same
as that
of
the
vertical
cylinder
except
that
the calculations
of
air
volume
and
its
compression
must
be
done
differently
(Fig.
4.l1).The
area
of
a segment
of a
circle
which
subtends
an
angle
of 0
rad
at
the
centre
Fig.
4.12- The
cross-section
of the
air
vessel.

120
is
given
by
Boundary conditions
lch.
4
(0
-
sin 0)
The
area occupied
by air
in the cylindrical cross-section
is
given by
Auir: nR2
-
A
So
the
volume
of air
in the
cylinder is
V^ir: A^irLr
The
relationship
betwen
the
central depth of
the air
vessel
and the
angle 0
is d
:
R[1
-
cos(0/2)]. The
variable
lr, which is the depth
in the tank is the same
as d above.
The
only difference
between the two
analysesis
in the
calculationof
hJh*;
which
equals
the ratio
of
the
volume of air at the current
time
to
the
volume
of
air
initially
present
raised to the
power
of
y.
These
volumes must
first be calculated,
using the
relationships above, and
their
ratio evaluated.
The rest of the calculation
then
follows
and the entire
analysis
can be
completed
with little difficulty.
4.f33 The surge tank
The surge
tank
is an excellent
device for controlling
transients.
It works
consistently
and
needs
no rnaintenance.
Like
flywheels,
its
operation
depends
solely
upon
its
physical
proportions. Its sole
defect consists
of
its limitations in use.
The
height of
a
surge
tank
is
limited by the
expense
involved
in its construction
and this
controls
the
circumstances in
which it can
be employed
(see
Fig. a.13).
There
are a
number of
different sorts
of surge
tank.
In essence they
all
work on
the
same
basis
but they use
different
techniques
of dissipating
the energy
of
the
mass
oscillation that occurs
in
them
and
employ
different devices
to damp
the
transient
pressure
waves that
are travelling
through
them.
The
normal
rnethod
of analysis of
a surge
tank consists
of a simple
application
of
the rigid column
method.
This works satisfactorily
in
that it describes
the mass
oscillation but
does
not describe
the
passage
of any
pressure
transients.
It is
not
generally
realized
that,
unless
the surge tank
offers an
infinite area
to the
flow
in the
pipeline,
there
will
be
a small
but
finite-sized transient
wave
which will be transmit-
ted
past
the
junction
of
the
surge tank
with the
pipeline
into
the system
beyond
it.
This in
many circumstances
will
not
matter; occasionally
the transient
will
pass
the
junction
at a frequencywhich
will
excite
resonance
in the
pipework
downstream
with
the
possibility
of
failure. See
Chapter
9
for a discussion
of resonance.
Additionally
there is
a
significant
risk that,
the transient
which
arrives
at the
junction
with the
surge tank, will have
been
travelling
in a
pipe which
is
capable of
withstanding
the
pressure
to which it is exposed,
but
it may
happen that the
considerably
attenuated
transient that
passes
up
into
the
pipe
upstream
may still
have too
large
a magnitude
for the
pipeline
to
withstand.
It is
therefore
important
that the analysis
of surge
tanks
Sec.4.13l
The
analysis
of air
vessels
t21
three
or
four
valves
sealed
toP
located
around
the
I
periphery
of
the
i
choke
outward-opening
valve
inward-opening
va lve
enlarged
view
of
valve
system
Fig.
4.13
-
The
choke
ring surge
tank.
should
be based
on
a
full
characteristic
treatment
and
not
on rigid
column
theory.
Commonly
analyses
of
surge
tanks
are still
carried
out
using
rigid
column
theory
but
now
that
this much
more
accurate
analysis
is available
it seems
quite improper
to
use
an
inferior
technique.
The
analysis
of the
air
vessel
given before
can
very easily
be
adapted
to
provid-e a solution
of
the simple
surge
tank.
If
the
vertical
rylinder
air
vessel analyiis
is
modified
by setting
the
height of
the cylinder
to a
very large
number,
the
solutioo
*itt be that
of a
simple
surge
tank.
Models
of
more
complex
surge
tanks
can
be constructed
using
the
usual
assumption
that
once
inside
the
surge
tank
the
rigid
column
assumption
is
valid.
Above,
this
rigid column
assumption
was used
to
dJscribe
conditionsinside
the
air
vessel
also. The
characteristic
technique
should
be
retained
in the
pipework
leading
to and
from
the surge
tank.
The simpl"
ioig"
tank
consists
of
a
vertical cylinder
rising
from its
junction
with
the
pipeline
to
a
height
at
least
20%
higher
than
the
highest
level
that
the
water
surfice
ever
attains.
On
the
downswing
the
level should
not
fall
lower
than
an
elevation
of.20%
of
the total
tank
height.
This
provides
an
adequate
margin
against
overtopping
or
the release
of
air
into
the
pipeline. Its analysis
is
performed
using
the
air
vesiil analysis
given above
with
the height
of
the air
vessel set
to
a
very
large
number as
mentioned
earlier.
4.13.3
The choke
ring
surge
tank
The choke
ring
surge
tank
consists
of
a normal
simple
surge
tank
across
the
inlet
of
which is fitted
idevice
resembling
a
top
hat. In the
vertical
sides of
this
device
are

122
Boundary
conditions
lch.4
fitted a number of check
valves which
open and
permit
a
restricted
flow into
the
tank.
When the flow direction reverses,
somewhat
smaller
check
valves, fitted
in the
leaves
of
the main
check
valves,
open and
permit flow
out of the surge tank into the
pipeline.
The
flow
is restricted
in both directions, less
for
flow in and more for
flow
out
of the tank. This restriction
dissipates
and attenuates the
mass oscillation and
also tends to
prevent
resonance. The flow in the
pipeline
just
upstream of the
junction
must
equal
the
flow into
the surge tank
plus
the flow
that
travels on down the
pipeline
away from the
junction.
So
A(i)u*,'
or#+ A(i+
1)u* .
(This
is the
same equation
as
was
used for the air
vessel
case.)
Ndenotes
the nodes at
the
junction
with
the surge
tank at time level /. From this
equation the
value
of.dhldt
can be obtained.
d/,
_
A(i)ul(i,
netno(i))
-
A(t + 1, 1)u1(t + 1,
1)
AT
where
i is the
pipe
number of the upstream
pipe
and
i * 1 is the number of the
pipe
downstream
of
the surge tank.
From dhldt
the
depth of liquid in the tank at the
end of a Ar
period
can be
calculated.
hrr: hr,+fftt .
Now
the head
in
the tank must be less than the
head
in the
pipe
at
the
junction
by the
amount of
kuluf2g
where u is the
velocity
through the
choke.
The
energy loss at
the
choke
due to the expansion
of flow
after it is
given
by this term and it
can be
seen that
it will reverse its direction
when
the flow reverses.
The
head
at the
junction
becomes
h2(i,netn'o(i))
=
Z +
hr +
h^ + Or,*
ry
where
fto is
the
height
of
the
water
barometer. This is the absolute
head at the
junction.
The value
of
k will have one
value when the
surge is rising
and
a
larger when
the
surge
is
falling.
This
is
because the larger chokes are in use when
the
surge
is rising
and
the smaller chokes
when
the surge is
falling. The
two characteristic
equations can
then
be used
to obtain the
values of the two
velocities
at the surge tank
junction
at the
t + Lt
time level.
dt
Sec.
4.141
Line
pack
and
attenuation
123
4.13.4
The
Johnson
differential
surge
tank
The Johnson
differential
tank is
a
surge
tank
with
special
qualities
in
that it is capable
of
causing rapid
attenuation
of
an oscillation
and is
unlikely to
generate
consequen-
tial frequencies
which
are
liable
to resonate
with the
governor
of
the
turbine
(see
Fig.
4.14).
open
top
(weir
flow)
orif
ices
Fig.
4.14
-
The
Johnson
differential
surge tank.
When shut-down
of
the
pipeline occurs,
forwhatever
reason,
the
level rises
in the
surge tank
and initially
in the
riser
only.
As it rises,
however,
flow out
through
the
base orifices
occurs
and
the
level starts
to
rise
in the concentric
outer
riser. When
the
level reaches
the top
of
the
inner riser,
a
weir flow occurs over
the
circumference
of
the top
edge of
it.
Eventually
the flow occupies
the entire
cross-section
of the tank
and the surge
reacies
its
maximum
amplitude.
The
surge
then
starts
to
fall but the
sequence
of events
is
not the
reverse
of the
events
that
occurred
during
the rising
surge.
The surge
falls,
at
first like
that in
a simple surge
tank;
then,
as
the surface
approaches
the level
of
the
central
riser, a
weir flow
will develop
down into
the
riser
of
smaller
diameter.
Once
a level
difference
between the surface
over
the outer
riser
and
the inner
riser
develops,
a flow
out of the
base
orifices into
the
inner
riser starts.
The level
in
the inner
riser falls
rapidly
and
the flow out of
the
orifices
is needed
to
stop
the level
from
falling
too far
and letting
air out of
the
surge
tank
into the
pipeline.
This sequence,
although
complex,
can
be
programmed
using
methods
similar
to those
demonstrated
in the
analysis
of
the choke
ring surge
tank.
Surge
tanks can
be used
in
the control
of
transients in
pipe networks
and also in
stabilizing
hydroelectric
systems.
As a
generalization it is
possible
to say that surge
tanks
are
more usually
encountered
in hydroelectric
schemes
and
air
vessels in
pipe
networks but
this
is a
very
general
statement
and
many exceptions
exist.
4.I4
LINE
PACK
AND
ATTENTUATION
When a
valve closes
rapidly
at the
downstream
end
of a
pipeline,
a steep-fronted
wave travels
upstream
at the
local acoustic
velocity.As it starts
off
to travel
upstream,
124
Boundary
conditions
the wave reduces
the
velocity
to zero
initially,
but,
as it
progresses
upstream,
the
pressure
that
it runs over
is an increasing
pressure
because,
as it
progresses upstream,
it
encounters
pressures
which are
greater than the
downstream
pressure
because
of
friction.
As it
reduces
the
velocity of
successive
layers
of fluid, their
pressures rise
and this rise
is transmitted
downstream
through
the
near- stationary
fluid, maintain-
ing
and increasing
the downstream
rises
which have
already occurred.
This
process
occurs at
wave speed
also.
Thus the
space
between
the
wave and
the
valve
is occupied
by
fluid which
has
had its
pressure raised
by the
momentum
change
in the wave
itself,
and also
by
the transmission
into
it of the increasing
pressure that the
wave
is
experiencing
as it runs
up the
hydraulic
grade line.
The section
of
pipe
thus
exposed
to
this
rising
pressure
is
distended
by
it and the
fluid
that it contains
is compressed
so
that, although
the
velocity
of
the
fluid
downstream
of the
wave is zero
when it is
located
at the
valve, this
velocity
progressively increases
as the
wave
progresses
upstream.
The
velocity
change
across
the
wave
thus
decreases
and
the wave
therefore
diminishes
in
magnitude
as the
wave
passes up
to the upstream
end.
This
diminution
in the
size of
the
wave is
called
attenuation
and
the
rise
in
pressure
as the
wave
travels
upstream
is called
line
pack. Attenuation
is
the
mechanism
that dissipates
the
wave
as seen in
Fig.
4.15-
Fig.
4.15
-
Attenuation
in the
Presenoe
of friction.
Line
pack
is
not
very noticeable
in short
pipelines but can
be
very
important
in
long
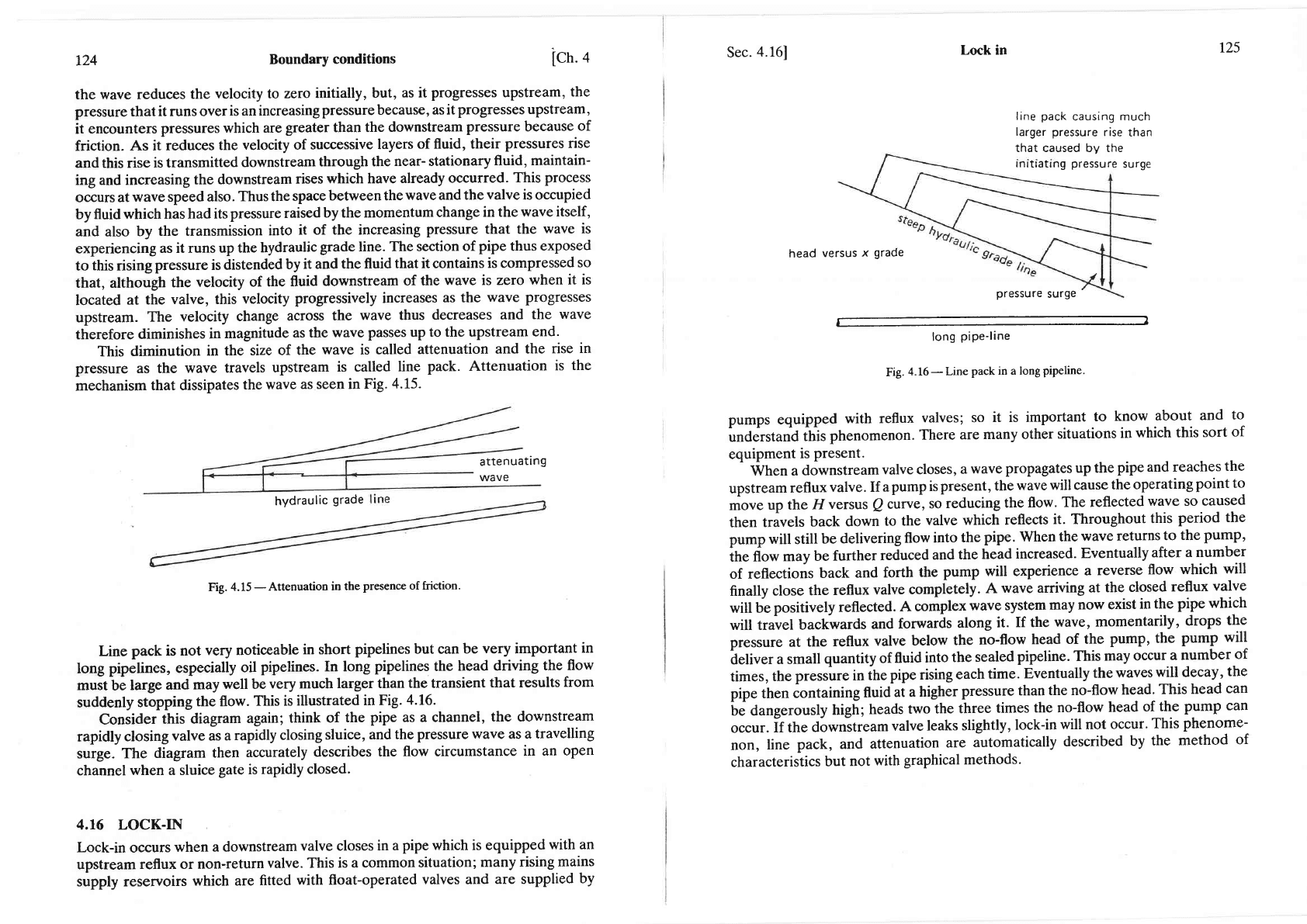
pipelines,
especially
oil
pipelines. In long
pipelines
the
head
driving
the
flow
mustbe large
and
may
well be
very much
larger than
the transient
that results
from
suddenly
stopping
the flow.
This is illustrated
in Fig-
4.16.
Consider
this
diagram
again;
think
of
the
pipe
as a channel,
the downstream
rapidly
closing
valve as
a
rapidly
closing
sluice,
and
the
pressure
wave
as a
travelling
surge.
The
diagram
then
accurately
describes
the
flow
circumstance
in
an open
channel
when a sluice
gate is
rapidly closed.
4.16 LOCK-IN
Lock-in
occurs
when
a downstream
valve
closes
in
a
pipe
which is equipped
with
an
upstream
reflux or non-return
valve. This
is a common
situation;
many
rising
mains
supply reservoirs
which are
fitted
with float-operated
valves and
are supplied
by
[cn.
a
attenuating
wave
hydraulic
grade
head
versus
x
grade
line
pack
causing much
larger
pressure
rise
than
that caused by the
Inrtratrng
pressure
surge
pressure
surge
Sec.4.16l
Lock in
long
PiPe-line
Fig.
4.16
-
Line
pack in a long
pipeline.
pumps
equipped
with
reflux
valves; so
it is important
to
know
about
and
to
unOerstand
ihis
phenomenon.
There
are
many other
situations
in
which
this sort
of
equipment
is
present.
-
When a
downstream
valve closes,
a
wave
propagates
up the
pipe
and reaches
the
upstream
reflux
valve. If
a
pump
is
present, the
wave
will cause
the operating
point
to
-on"
up the
.I{
versus
Q
iuwi,
soreducing
the
flow.
The reflected
wave
so caused
then
trivels
back
down
to the
valve
which
reflects
it. Throughout
this
period
the
pump
will
still
be
delivering
flow
into
the
pipe. When the
wave
returns
to
the
pump,
itt"
tio*
may
be
further
reduced
and
the
head
increased.
Eventually
after
a number
of reflections
back
and
forth
the
pump will experience
a
reverse
flow
which
will
finatty
close
the
reflux
valve
completely.
A
wave arriving
at
the
closed
reflux
valve
will be
positively
reflected.
A complex
wave
system
may
now
exist
in
the
pipe which
will trjvel
backwards
and
forwards
along
it.
If the
wave, momentarily,
drops
the
pressure at the
reflux
valve
below
the
no-flow
head
of the
pump,
the
pump
will
'deliver
a small
quantity
of
fluid
into
the
sealed
pipeline. This
may
occur
a
number
of
times,
the
pressure in
ihe
pipe rising
each
time.
Eventually
the
waves
will decay,
the
pipe then
iontaining
fluidat
a
higher
pressure
than
the no-flow
head.
This
head
can
^b"
dung"tously
high;
heads
two
the
three
times
the no-flow
head
of
the
pump
can
occur.
it ttt"
downitream
valve
leaks
slightly,
lock-in
will not
occur.
This
phenome-
non,
line
pack, and
attenuation
are
automatically
described
by
the
method
of
characteristics
but
not
with
graphical
methods.
125

Turbines
5.1
INTRODUCTION
The
analysis
of
a hydroelectric
scheme
is exactly the same as the analysis of any other
pipe
network except
for the special boundary
conditions
presented
by the
turbines.
Generally,
a hydroelectric
scheme
is a
very
expensive
project;
so its safety
is of
great
importance. Even
small
schemes
involve the handling of significantly
large flows of
water of
high energy;
so there
is always some risk
and this must be minimized.
The
turbine is a
device for
converting the energy
which water
possesses
by
virtue
of
its elevation
in the
earth's
gravity
field, i.e.
potential
energy to rotational
energy
which can be used
to
drive an electrical
generator.
It is assumed that readers
have
studied
the turbine
in their
first degree course
and know how it works.
There are
three
main classes
of turbines.
(1)
For high head
circumstances,
these
are as follows.
(a)
Impulse
turbines.
This consists of
the Pelton wheel in its
various
manifes-
tations, such
as single-jet
machines, multiple
jet
machines and
multiple
wheel-machines.
These all have
low
specific speeds
(ranging
from 9.5
to 23
kW m
rev/min).
(b)
Turgo wheels.
These
machines have
rather
higher specific speeds
(ranging
from 30
to 46)
and so can handle
somewhat lower, but
still
large, heads
and
larger flows.
This machine is
not as
popular
as it should be.
(2)
Radial flow
machines.
This class contains a
large range of different
types of
machine from
the
pure radial
flow Francis
turbine, capable of handling
large
heads
and
having
a fairly
low
specific speed
(ranging
from 46 to 76)
through
Sec.
5.11
Introduction
mixed radial-axial
flow machines,
which handle lower heads
and
have
larger
specific
speeds,
to
the nearly
axial flow machine,
which handle low
heads
and
have specific
speeds
ranging
up to 570.
(3)
Axial
flow machines.
This class
consists essentially
of three
types
of turbines:
the
propeller
turbine,
the
Kaplan
turbine and
the bulb turbine.
These
machines
are
very large and
require
very large
flows under small
heads.
The
principles
under
which turbines
operate
are exactly
the same
as those
for
purnps
and, indeed,large
radial
flow
pumps
may be
constructed
in exactly
the same
way as
turbines. Machines
used
in
pumped storage schemes
work alternately
as
pumps and
turbines.
It is not surprising
that
the theory
of
pumps
and turbines
is
identical
except
that a
pump
uses energy
to
generate head
and a turbine
uses
a head to
generate
energy.
To analyse such
machines
and the
associated
pipe
network
it is
neressary
to have
detailed
information
about
the machines'characteristics.
Analysts
use
various
forms
of
the characteristic
curves
of
the turbine
that
they wish to
analyse.
It is suggested
that
the
Suter
presentation
is the
best as
it covers all
possible
modes
of operation
of
any
turbine using
only
one
diagram.
This
presentation has been
exhaustively
described in Chapter
4 and
the
reader
is recommended
to familiarize
himself
with
it
before
proceeding. There
is one
difference
between
pumps
and turbines
and
this
is
the adjustable
guide vanes
which are
present.in
turbines
but only
exceptionally
so in
pumps.
Usually
these
adjustable
guide vanes are called
the
wicket
gate
and
act as a
flow control
device.
The
wicket
gate
has
two functions:
it controls
flow by
altering
the
area available
for flow
and
also adjusts
the angle
at which the
absolute
velocity
enters
the
runner.
For
every
value of
the
wicket
gate
setting
there
are two complete
Suter
graphs,
i.e. for the
Wpagainst
0
and
for the W7 against
0
graphs
(see
Chapter
4).
Thus it
is necessary
to
plot two
graphs
for each
of a
number of
wicket
gate
settings
so
that
it
will
be
possible to
interpolate
between
them for
any
given
value of
0
and
for
any
wicket
gate
setting.
It is
necessary
to use
graphs
for at least
1,0
wicket
settings-
It is
recommended
that
parabolic interpolation
be used
when obtaining
values
for
intermediate
wicket
gate
seffings.
To do this the
following
procedure
may
be used.
For a
wicket
gate
setting
of
w at
a
value
of 0
equal
to 0rfind
three
values
of
Ws for
wicket
settings
of
w,-r,
w, and
wr*,
where wlies eitherbetween
wt-r and
w,
or
between
wrandwi+t.
Then Wu:
cr*
pw
*'!w'. Now,
when
w:wi-,
then
Wa:
W*q., and similarly
for the
other
two
values of
w;
so
Wr,-r:
q*
FrYr-r
*
Tw?-rz
,
Wr,
=d*F*!+yw!
,
W
*,*r=d
*
Fw
,*,
*
'{w7*
,.
From these
three
equations,
c,
p
and
y
can
be calculated.
Then Wrcorresponding
to
the
wicket
gate
setting
w at0i
is
given
by
r27

r28
Turbines
lch.
s
Wa:a*pw*Y*'
Similarly
the
value of.
Wrcan be obtained
by
parabolic
interpolation
also.
Once
W, and lllz.
have
been obtained,
the
values of flow
and head
across
the
turbine can
be obtained
by methods
exactly
the same
as
those used
for the
pump
given in the
previous chapter.
One
problem
remains.
This is
how the
value of
w- the
wicket
gate
setting
-
applicable to
the
next
Arperiod can
be obtained.
For
a turbine,
circumstances
external
to
the hydroelectric
station
decide
the
power that
it is
required
to
provide. Additionally
it
must
generate
power at a fixed speed
so that the
alternators
that
convert
the
power
generated by the
turbine
to
electrical
power
can
do it
at a
determined
frequency.
In
the UK,
an electrical
distribution
network
has
been
developed
which operates
at 50
cycleVs;
in the USA
the frequency
of
their
distribution
networks
is 60
cycles/s
and
any
power
station
that
is to be
connected
to
such systems
must
generate at
these
frequencies.
This requirement
demands
that
speed
regulation
is
accurate
under
steady
and
fluctuating
loads.
To achieve
such
a
high
standard
of speed
regulation,
governors
have been
developed
which can
ensure
that the
turbine
will operate
at the
required
synchronous
speed.
5.2
TURBINE
GOVERNORS
The
turbine
governor is required
to
respond
to
a variety of speed
fluctuations
ranging
from
full shut-down
to
start-up.
There
is a drop in
the speed as
a turbine
takes
more
load and
the
difference
between
the steady
running speed
at full
load and
the speed
at
no load is
called
permanent speed
droop.
In response
to a
rapid decrease
in
load
the
turbine
will increase
its speed
and the
governor must
close
the wicket
gate
so
that
the
generated
power
will equalize
with
the
load demand.
Initially
the
governor
must
cause
a
wicket closure
which
will cause
the speed
to reduce back
to
its steady
synchronous
value. The
wicket must
be closed
by a
greater
amount
than
would
give
the steady
synchronous
speed
so
that there
will be a
rapid reduction
in speed
to a
value followed
by
a relatively
short
period of further
speed
reduction
down
to the
synchronous
speed
(see
Fig.
5.1(b)).
To
do this,
temporary speed
droop
is
used.
This
is a feedback
signal
which
is
proportional
to the rate
of movement
of the
wicket
gate
servomotor
the
signal
decaying expenentially
with time
.
It is
possible to
achieve
a condiction
in
which there
is no change
of speed
with
changing
load.
This
is called'astatism'.
There
is a
number
of designs
of
mechanical
governors
that can
produce the
behaviour
required,
but
now electrical
devices
are also available
which can
operate
as efficiently
as
mechanical
governors.
The
turbine
governor
generates the
required
value of the
wicket
gate
setting
w
for
the time
level
r *
At which
can then
be used,
as described above,
to obtain
the Wp
and lV2"
values. Once
these
are available,
the
flow, the speed, the
head
across
the
machine
and the
power
generated
can
all be calculated.
The methods
to
be
used in
performing these
calculations
are
the same
as those
used
earlier for the
analysis
of
pumps.
Fig.
5.1-The
effect
of a
governor
(a) with
permanent
droop-but
without temporary
droop,
(b)
with
permanent and temporary
droop.
Sec.
5.21
Turbine
governors
r29
synchronous
speed
correct
rate of
withdrawal of
temporary droop
\
temporary
droop withdrawn
too slowly

Boundary
conditions
continued.
Junctions,
valves,
friction
and
wave
speed
6.I
JUNCTIONS
An analysis based
on
the
method
of characteristics
can only
be solved
by computer
methods.
The
load of
calculation
is far
too
great to be handled
any
other
way. Any
use
of
a
computer
requires
the
writing of a
program. This
consists
of a number
of
shorter
pieces
of
program sometimes
called
subroutines.
Each subroutine
performs
tasks
which the
analyst
requires;
for
example, a subroutine
to solve
an upstream
reservoir
to
which
a
pipe
is
connected
could be called UPSTR
(in
Fortran IV
the
name of a
subroutine
is limited
to six
characters
only
and Fortran
IV is the
commonest
computer
language
and
the most
widely distributed). Subroutines
for
pumps,
airvessels,
downstream
reservoirs,
valves, turbines,
junctions,
etc.,
together
with subroutines
for data
input and
output,
will all be required.
Additionally
a
subroutine
(usually
termed
the
main
program)
is needed
in
which
the other
subroutines
are
called,
in
appropriate
sequences,
to do the
work
necessary
to solve
the
network.
As far
as
networking
is concerned,
the
junction
subroutine
is
the most
important
subroutine
that
the analyst
will
be
called upon
to develop.
Such
a
subroutine
must
have the
following
characteristics:
it must have
no limitation
on
the
number of
pipes
joining
at
the
junction
and the subroutine
must
be
capable
of
detecting
the direction
of
flow
in every
pipe
joining
there.
The knowledge
of
which
end
of a
pipe is meeting
others
at a
junction
is
vital,
because,
at a
junction,
the
head
is
the same for
every
pipe meeting
there,
and
the
assignment
of this common
head
must
be made to
the head
array
positions appropriate
to the
nodes
in the network
at
which
the
pipe
ends
are located.
Also
the
velocities at
these
ends
must be calculated
and
the
results
assigned
to the
velocity
affay
positions
appropriate
to
these same
nodes.
At this
point it is
necessary
to
demonstrate
the method
that the
author
uses to
define a network.
It
is not
the
method
that is in
common use
-
which is the
node
method
-because
the
author
considers
the link method
to
be superior,
in that
it has
Junctions
r31
Sec.6.1l
the advantage
of
using
the
absolute
minimum
of
information
necessary
to
define
the
network.
First
a schematic
diagrarn
of
the
network
must
be
prepared
and
oneach
pipe an
arrowhead
must
be
dralwn
indicating
the
direction
in
which
the
analyst
thinks
it
probable
that
flow
will occur.
The
diriction
may
be chosen
wrongly
but
if so
the
only
.onr"qrr"nce
is
that
the
computer
will
calculate
the
flows
and
velocities
in
such
a
pipe
as
being
negative,
i.e.
opposite
in
direction
to
that
that
the
analyst
thought
would
occur.
Next,
number
ealtr
pipe,
continuing
the
numbering
across
every
boundary
condition
sequentially;
the
bnty
"*""ption
to
this
rule
occurs
at
a
junction
at
which
more
than
two
pipes *."t.
The
information
necessary
to
solve
a
junction
consists
of
the
following
data-
(7)
n,the
number
of
pipes
joining
at
a
junction'
tZi
1.it
numbers
of
'the
iip.t
joining
at
the
junction
signed
according
to
the
following
convention:
positively
signed
if the
pipe has
been
considered
to
be
transporiing
flow
towards
the
junition
and
negatively
if
the
pipe
has
been
consibered
to
be
transporting
flow
away
from
the
junction.
(3)
The
number
of
Ar
nod"r
in
each
pipe length
+ 1.
This
information
will
have
been
required
in
the
main
program
and
*ilt
be available
and
will
not
need
to
be
specially
supplied.
The
auihoi
uses
an
array,
netno
to
contain
this
number
for
each
piPe.
(a) The
diameters,
lengths
and
roughnesses
of each
pipe'
only
irems
(1)
and
(2)
above
will
need
to
be
supptied
as
information
specifically
associated
with
the
juncti,on.
Items
(3) and
(a) will
have
to
be
supplied
when
loading
input
data
associaied
with
all
the
rest
of
the
program
and
are,
thus,
generally
required.
For
each
pipe
meeting
at
the
junction
calculate
an integer
number
l'. This
number
is to
be
+
1 if
the
numbei
of
the
pipe is
positive
and
-
f. if
the
number
is
negative.
It
can
be
calculateJ
from;"-TlaUsf)
toit"t.
i
is
the
pipe number'
The
continuity
equation
must
apply
at the
junction;
so
,>r*iJ''uo:o
where
A, is
the
area
of
the
ith
pipe, uo
is
the
velocity
at
the
t +
Lt
time
level at
the
junction
a
nd
mis
the
number
of
pip.t
ltiining
at
thejunction.
This
is a
statement
that
ilow
towards
the
junction
must
equal
the
flow
away
from
the
junction'
Then
for
every
pipe meeting
at
ihe
junction
the
wave
equation
can
be
written:
i"
:
(ho,-
h,)
+Do,
-
u,
*'ff
:,
In
the
foregoing
the
subscript
i
denotes
that
the
variable
so
designated
is
that
for
the
ith
pipe in
itre
jirnction.
uo
denotes
the
velocity
at
the
second
time
level,
i'e'
at
time

r32
Boundary
conditions
continued
fch.
6
t +
Lt
at
the
junction
itself
and u,
denotes the interpolated
value
at
the
base of the
characteristic line
rising up from
the
interpolation
position
on
the ith
pipe
at the time
level r. From this
equation,
a
value
of uo_ can be
obtained:
Sec.
6.21
Valves
r33
Chapter
13 but here
an outline
is
presented. Remember
the
signed
numbers
which
originally
were used
to specify
the
pipe numbers of
pipes
joining
at
the
junction
and
how
they specify
whether
the
pipes
are transporting
water to the
junction
or away
from it. Remember
also that
the sign of
the number was
positive if
the
pipe was
transporting water
towards
and
negative if transporting
flow away
from the
junction
and also that
the
value of i" was
set
to
1
if the
sign
was positive and
-
f.
if it
was
negative.
Then,
if for any
given
pipe
the
value
of
r, is
greater than
zero,
the
characteristic
equation
for that
pipe
will
be a
positive
one
and the
value
of the
downstream
Ax
node
number
will be netno(l).
If for any
given
pipe
the
value
of
i" is
less than
zero, the
characteristic
equation for
that
pipe
will be a
negative
one
and
the
value
of the
upstream
A-r node
number will
be 1. By
performing this
assignment
process
for all
pipes
joining
at the
junction
sequentially,the
appropriate
value of the
node number can be
calculated
and the
velocities
and head at
the
junction
assigned
to
their appropriate
positions
in
their arrays
for each
pipe.
6.2
VALVES
Usually
a
valve
is situated
between
two
lengths of
pipe
but
not always so.
In the case
of
reservoir
valves,
a
valve may
be located in
the
wall
of a tank and
so there
will
only
be one
pipe
bringing
or taking
away
liquid to or from
the tank.
Any subroutine
must
provide
facilities
for dealing
with
these two cases.
Additionally,
the
way in
which the
valve
is controlled
can
differ
widely from
valve to
valve.
For example,
a
valve may
be
manually
controlled
or operated
by a
gear
box driven
by an electric
motor.
Such
motorized
valves
may
have
different
patterns
of
operation;
one
gear
box
may shut
the
valve at a steady
rate
throughout
the closure
while another may
perform its
first
nine
tenths of closure
rapidly and
its last tenth
very
slowly,
So
generating
minimal
pressure
transients. Such
valve operation
is direct and
immediate
but controls
may
operate
to maintain
pressures
or
flows at
distant
points
in the
network. Servomecha-
nisms can
be employed
to open
or close
valves
in a controlled
manner
so
that
various
parameters,
e.g.
a level
in a
tank, can be
varied in a
very defined
way.
Again,
valves can be of
very
different
types.
For
example
a sluice
valve
is
very
different
from a
globe valve. From the analyst's
point
of
view this
hardly
matters.
As
will be explained
later,
to him a
valve is only
an array of numbers
in
his computer
program,
the arrays
being
different
for dffierent types of
valves. A
valve affects
the
flo* thto,.rgh
a
pipe
by offering
a resistance to
the flow that
can be adjusted
at
will.
In
essence
the
valve causes the
liquid to
lose
energy.
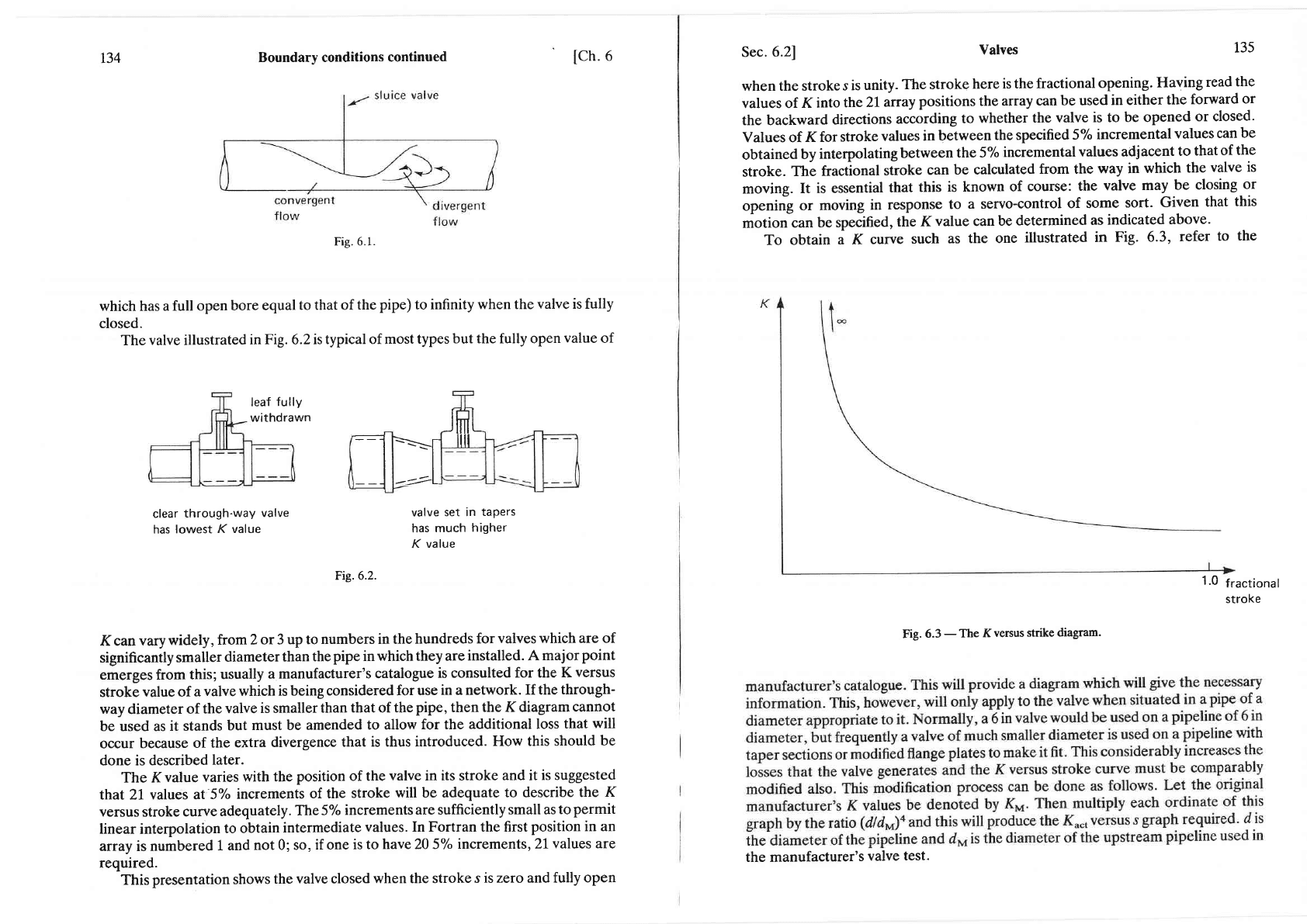
It does
this by
presenting
to the
flow a convergent
passage
followed
by a rapidly
divergent
passage
(Fig.
6.1).
In
the
convergent
passage
the liquid
increases
its
speed
greatly
and in the
divergent
passage
a boundary
layer separation
occurs
which
generates heavy losses.
The
degree
of
convergence
and consequent
divergence are adjusted
by altering
the
valve's
setting.
The
loss is
given
by
a
simple
equation
,,
Ku2
nr__E
where
K is a constant
ranging from
low values as low as 2 or 3
(for
a fully
open
valve
uo,: u,
(ho,-
D-zfu#!
,Z-r^('^''-
i?A'€r,0,,*
i?At:.ht-in4tzf'y)u'l
Lt)
:
o
but 1,2:
1.
So
and this can
be substituted
into the continuity
equation
to
give
or-
hoo2*
o:
-
o+:0
Therefore,
as ho is the same for all values
of i
where
\
o1:
L
i/iDi
,
,m
sA5
oz:
L
. f?l
\r
Agh,
03:
L
-,
.m
s
in4,2ftu,lu,l
Lt
04:
Z
,:r',*
di
From
the result obtained
for ho,,
calculate
all the
values
of uo, from Do,:
u,
-
i"(glc)(ho;h,)
-Zf,u,lu,l
Lttd,using'all the values
of
i,
the numbers
oipipes
j6ining
at
the
junction.
Once
these
values
have
been calculated,
the
junction
has
been solved
but
there remains the
problem
of assigning
all
the
values
to their correct
positions
in
the
appropriate arrays.
The
precise
manner
in which
this is done
is demonstrated in
t34
Boundarv conditions
continued
fch.
6
Fig. 6.1.
which
has a full
open
bore
equal
to that of
the
pipe) to infinity
when the
valve is fully
closed.
The
valve illustrated
in
Fig.
6.2
is typical
of most
types
but the fully open
value
of
JffiL
I
_\\*
-tt-
ill
clear
through-way
valve
has
lowest
K value
valve
set in
tapers
has
much
higher
K
value
Fig. 6.2.
K can
vary
widely,
from
2 or 3
up to
numbers in the
hundreds
for
valves
which
are of
significantly
smaller
diameter
than
the
pipe
in
which they are
installed. A
major
point
emerges from
this;
usually
a manufacturer's
catalogue
is consulted
for the
K
versus
stroke
value
of
a
valve which
is being considered
for use
in a network.
If the
through-
way
diameter
of
the
valve
is smaller
than
that of the
pipe,
then
the K diagram
cannot
be used as
it stands
but
must be
amended
to allow
for the
additional loss
that
will
occur
because
of
the
extra
divergence
that
is thus introduced.
How this should
be
done is
described
later.
The K
value varies
with the
position of the
valve
in its stroke
and it
is suggested
that 2l
values at
5o/o
increments
of the
stroke
will be adequate
to describe
the
K
versus stroke
curve
adequately.
The
5%
increments
are sufficiently
small as
to
permit
linear
interpolation
to obtain
intermediate
values. In Fortran the first
position in an
array is numbered
1 and
not 0; so,
if one
is to
have 20 5%
increments, 21.
values are
required.
This
presentation
shows
the
valve closed
when the stroke
s
is zero and fully
open
leaf
fully
withdrawn
Sec.
6.21
Valves
135
when
the stroke
s
is
unity.
The stroke
here is
the
fractional
opening.
Having
read
the
values of
K into
the2larray
positions the
array
can
be used
in either
the
forward
or
the backward
directions
according
to
whether
the
valve is to
be opened
or closed-
Values of
K for stroke
values
in
between
the
specified
5%
incremental
values
can
be
obtained
by
interpolating
between
the 5%
incremental
values adjacent
to
that of
the
stroke.
Th!
fractional
stroke
can
be calculated
from the
way in
which
the
valve
is
moving.
It is
essential
that
this
is known
of
course:
the
valve
may
be
closing
or
opening
or
moving
in
response
to
a servo-control
of some
sort.
Given
that
this
motion
can
be specified,
the
K
value can
be
determined
as
indicated
above.
To obtain
a K
curve
such
as
the one
illustrated
in
Fig. 6.3,
refer
to
the
1'0
fractional
stroke
Fig.
6.3
-
The
K
versus
strike diagram.
the manufacturer's
valve
test.
