Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

76

The method

of

characteristics

I

dh

,

du

,

2/ulrrl

J.!-n

cdt dt d

+&

(t

"-

h*) *

up-r*

*

fu19d4-

o .

'

c

.'--

'-K/

-

r

-.(

d

Along SP the negative

characteristic

equation applies:

fch.3

Generallv

and

dJ

ts*c

When

the

positive

sign

is

used, a characteristic

line in

a

t-x

space is obtained, of

gradient

tl(u+c), and along which

the expression

(g/c)dhldt*duldt+Zfululld

is

zero. When the negative

sign is used, a negative

characteristic

line is

produced

in

the

r

versus.r

spare along which the

expression

-

(glc)

(dhldt*

duldt+Zfululld

is zero.

Some

analysts refer to these

two characteristics

as forward

and backward characteris-

tics because the

positive

characteristic

line has a

positive

slope and information is

carried forward in an

x increasing direction

but, a negative

characteristic

usually has

a negative slope which

carries information

backwards

in an x decreasing direction.

There are

quite

a number

of circumstances in which

a negative

characteristic can

carry information

in an x-increasing

direction;

so the author does not

favour the

forward and backward

definitions.

Sorne

analysts

use the

phrase'world

line'in

place

of characteristic and this seems to be

a

practice

from the

world

of

physics.

The domain

of dependency

of

P in Fig.

3. 1 is the segment

of the

x

axis

RS in

which

events occurring, such as

velocity

fluctuations

or head fluctuations,

generate

fluctua-

tions

of

head and

velocity

at P. The range

of influence

of P in the space

-

in

the

r-r

sense

-

is

the

space

in which

events happening

at P arc

propagated.

The

domains of

indeterminacy

of

P

are the two zones in which

events in

the domain

of dependence

of

P

have no effect whatsoever.

3.2,1 The Hartree method

The

use of the characteristic

waterhammer

equations

can be demonstrated by

reference

to Fig.

3.1.

The

characteristic

equations must

first be

cast into finite

difference

form. Along the line RP the

positive

characteristic

expression applies; so

#9!+9e+

4ul:o

-cdt

'dr'

d

dt

Sec.

3.21

The method of characteristics

negat

lve

characteristic

77

fr

l+-

domain of

dependence

----->lS

ofP

Fig. 3.1.

-E

@r-

hr) *

t)p-r, +

&lldA:

o

c

,''.

'-J' ',

-r -r '

d

Subtracting

these equations

to eliminate

v

"

gives

,

h*lc + hlc

*

(u^

-

us)/g

-

FR + Ft)lg

'u,

where

F

Zf*u*lu*lLt

.^:T

and

"r:rynE

Note the use of

c in the above

equations.

It must be assumed

that

c is constant

over

the upstream and

downstream

A.r

values because the

two A.r

values

share

the

common

point

N, and over

the Ar interval also.

In other

words the

value

of c must

be

assumed constant

throughout

the space

defined by

the horizontal

and the

two

characteristic

lines

if the form

of the equations

given

above is

to apply.

As

both

Ax

and Ar are required

to be

small, if a finite

difference approach

is

to be

used, this

assumption

is reasonable

. The

use

of

a constant

value

for c is thus

j

ustified

. Therefore

(F"

-

fr)c

posrtrve

characteristic

range

of

inf luence

oIP

domain of

indeterminacy

domain of

indeterminacy

ofP

,

h** h,

,

(u^

-

u5)c

np:a-

-

Zg

2g

78

and

up:

DR

*f

<n,

-

h^)

-

FR .

If

hR,

y'ls,

D.* and

u5 are

known

then

F^

and

F,

can be

calculated

and

the values

of. h"

and

up

can be

determined.

A

complete

technique

of

analysis

can

be

based

on the

solutions

given

above.

As can

be

seen in

Fig.

3.2., characteristic

lines

are

curves.

This

is

caused

by the

zone

of

quiet

Fig.3.2.

variations

in u

and

c that occur

in unsteady

flow.

It is therefore

necessary

to

ensure

that

the

the r axis

is

divided

up into

A.r

lengths

which

are

so small

that the

corresponding

segments

of

the

characteristic

lines

are,

effectively,

straight.

The

Ar

value

corresponding

must

fit the

requirement

that

at

x

(u

+

c) + arx

lu

-

cl

:

Ax.

_

Divide

up the.r

axis

into

Ar lengths.

These

Ax

lengths

must

be

short

enough for

the

segments

of the

characteristic

lines

springing

from

their

ends and

rneeting

at

P

points

to

be,

effectively,

short

and

straight.

Complete

characteristics

are

curved

because,

in the

case

of unsteady

flow,

the values

of u

and c

change with

r and I

-

as

demonstrated

in

Fig.

3.2

-

and

so the values

of the

characteristics'

gradients

(l/(u

* c)

and ll(u

-

c)) must

also

change.

From

the nodes

so created,

pairs

of

positive

and

negative

characteristics

are

drawn.

These

characteristics

intersect

at various

positions

in

the

x-r

space.

The

techniques

for

calculating

hp and u" given

before

can

then be

applied

to solve

for

values

of

ft and

u at

all of

these

points.

There

are

problems

associated

with

doing

this,

however.

There

are

no

particular

difficulties

in

analysing

the

central

regions

of i duct

in this way

but

a

problem

arises when

the

boundary

nodes

are

to

be

solved. At an

upstream

boundary,

a negative

characteristic

is

available

to

provide

one

of

the

two

equations

needed

to

solve

the two variables

h

and u. The

other

equation

must be

provided

by

the

conditions

at

the boundary.

If a

reservoir

is locatedlt

the upstream

Sec.

3.21

The

method

of characteristics

boundary,

this is

very easy

to

establish. The required condition is simply

that the

pressure

head

plus

the

elevation of the centreline of the

pipe

above some chosen

datum

(the

total

head

h) is constant. This

provides

the head h and the

value

of

u

can

be

easily obtained

from

the negative

characteristic

invariant.

So

Dp: Ds

+

glc(h,

-

lt")

-

fs

where

Fs:2f5uslutltt/d,

d is the pipe diameter and

.fr

is

the

Darcy

friction

coefficient.

Similarly

downstream,

the

conditions

of the boundary there and

the positive

characteristic

joining

from

the

node

just

upstream

provide the

solution

for nodes

located on

the x:

L ordinate. If all boundary conditions

were

as

simple as the

reservoir

there

would be no difficulty in using this technique. Unfortunately,

this is

not so; many of

the boundary

conditions that can occur

offer

considerable

difficulty.

Junctions,

pumps,

turbines

and valves of many different sorts all

have their

difficulties

and can

be awkward to handle

in

this method.

An additional

awkward-

ness of this

method is

that,

as

time advances, the network of lines

gradually

distorts

and

becomes,

progressively, more and more irregular. This means that for

neither a

fixed x

value

nor a fixed

r

value

will

it be

possible

to obtain

more

than a few /r

or

u

values. Fig.3.2 describes

a

pipeline

in

which the flow

is

initially steady. It will

be

seen

that

below the

positive

characteristic

line originating at x

=

0 and

r:

0 the character-

istics, both

positive

and

negative, are

straight.

This is because the flow is

steady as no

unsteadiness

has reached

the nodes in these locations. Thus,

the

velocities

and wave

celerities

at each node

remain at their

previous values

until the unsteadiness

reaches

them and so

the characteristic

gradients

remain constant. This

zone

is

called

the zone

of

quiet.

If x

is large

there

may well

be a

number

of

P

points

lying immediately

above

the initial

node but,

as time

advances, the

point

of interest

passes

out of the zone

of

quiet

and

into that

area

of the diagram in

which

the network made

by the

characteristic

lines

is

distorted. Consequently, on an ordinate

located

at x, there will

be a number

of

P

points

for

which

h and

u

values

will

be available; for

larger

fvalues,

outside

the

zone of

quiet,

there

will

be

none except

coincidently. Similarly, for an x

line

drawn horizontally

on

the

diagram at a

particular

t value, there may

be no P

points whatsoever.

Values

can be

obtained

on either the x line or the r line

by

interpolating

values

from

adjacent

P

points"

This

method

is due to Hartree,

who

originally

developed

it

as a semi-graphical semi-computed

method in the

1930s. He

used hand-operated

mechanical

computing machines which must

have

been exceed-

ingly tedious to operate.

One can have only

the

greatest

admiration for

him. The

method

can be

programmed on a modern computer and

has certain considerable

advantages

but also,

disadvantages.

In

particular

it has a tendency to

generate

non-

existent

shocks.

3.2.2

The

method of

the

regular

grid

The early

attempts

to

program

the

characteristic

equations for modern computers

by

Streeter

and

Lai in 1963

used the

assumption

that

velocity

u

would

be

sufficiently

small, in comparison

with

the

celerity

c, that it

would

be

permissible

to ignore

it

(Fig.

3.3).

This assumption

is

also made in the

graphical

methods described in

Chapter

2.

The

method

of characteristics

lch.

3

t9

80

The method of characteristics

lch.3

l<-

Ax

+l<-

Ax

-->l+

[26

+l+-

[;

-->la-

Ax

-+l

x

E:^ 2 2 |.\-:-:-.1 Qfraa+ar I oi ma+hnA

L 16. J.J

-

VrlSrlrq 9llvvavl-Lsr

urvrrruv-

Flowever, this assumption

was only

made where it affected the slope of

the

characteristic lines

but it

was not

applied

within

the

characteristic invariant. This

meant that the slope of

the

positive

characteristic

became llc and

that

of

the negative

characteristic became

-

Llc. Then,

by starting a

positive

characteristics line from

the

upstream end of

a A.r and

a negative characteristic

line from the

downstream

end

of

the Ax a regular

grid

was

formed.

Such

a

grid

has a

mesh of

Ar, chosen by the analyst,

and a Al equal to

Lxlc.

Throughout such

a

grid, the characteristic slopes

are constant

and the

grid

is

completely regular as long

as the

wave

speed

c is constant

with

x

and t. This is a

very

convenient

property

and makes

it

possible

to

provide

tables, and

hence

graphs,

of

lr

against/orof uagainst

tatanymultipleof

Ax orof hagainstxorof

uagainstxforany

multiple of Ar. This technique

is not

wholely accurate and has been superseded

by the

method now commonly

used.

In the

current

method

(Fig.

3.a),

the

values

of

the

characteristic

slopes

are

Fig. 3.4

-

Current

method.

Sec.

3.21

The

method

of characteristics

evaluated

for

the

velocity

value and

celerity

value

current

at

point N, i.e.

l/(ur * crv)

and 1/(ur-

cru).The

negative

characteristic

line slope corresponds

to

an angle

p

(in

Fig. 3.5)

which

is

greater than

90".

The

angle

1

is

equal

to arctan(ll(c7,-

u,v) and is

smaller

than 90o.

The

two

characteristics,

with the slopes

evaluated

above,

are drawn

lrack from the ooint P to

intersec-t

the x abscissa below

P at

R and

S. Now,

the time

interval

PN

is chosen

to

be

a little

less than

the maximum

of

Axl(ur

* cn') and

Lxl(cv1-

uN);

so

R and.S

are

not

coincident

with the node

points Xand Y.

(Note

that

the

author

uses 0.95[luu/abs(u,

+ c,u)]

as

this,

in almost

all circumstances,

will

ensure

thatRandSwillliewithintheendsof

theline

XY.)Thevaluesof

ftR, un,hsandu5are

by interpolation;

the

values for the

point R are

interpolated

between

those

for X and

N and

the

values

for the

point .S

are interpolated

between

those for

N

and

Y. The

values at

P

can

now

be

obtained

from

the

invariants

of

the two

^l- ^ -^ ^+^-i^+i ^ li-^^ l^.' ^i-"1+a na^rrc cnlrrfinn

Ullall alutEl

lDLllv

llllgJ

trJ

Dllllurlallvvuo

ovrslrvrr'

To

do these

calculations

on

a computer,

first declare

two

arrays

of

variables.

One

array

is to contain

two

sets

of

lr values;

the first set

is

to contain

lr

values

for all the

nodi

positions

at time

level

t and

the

second

to contain

/r values

at all

of the node

valueJ but

at time

level

t +

N.

The

second

array is

to contain

two

sets of

u

values; as

for the

lr

values the

first set

is

to contain

u

values for all

the node

positions

at

time level

t

and

the second

to

contain

u

values at

all the

node

positions at time

level

t + Lt. An

h

value

for thelh

Ax

node

and

for

the

t

level

would read

h[i,1]

and

for the

t + Lt level

would

read

hlj,2].

Comparable

values

would

apply for

the

u array.

To

perform ttie

interpolation

process,

proceed as follows

(Fig.

3.5).

To interpo-

late between

thei

-

1

node

and

the.,1node.

i-1

j+1

Fig. 3.5

-

The

interpolation

process.

81

h^: h[i,

\-(hU'

tl-

W

1'

1])

dr

Similarly,

for

the

u^

value,

uR:

uU,11

-

(u['r' 1]

-

u[/'-

t

'

tl)

ar

where dx

:

dr(ull,

i

j

+ cU,

1i).

To

interpolate

between

the

j

node

and the

j

+ 1 node,

hs:hli,yW

Similarly,

for

the

urvalue

ut:u[',tt*W

the d.r

value for this

case

is

given by

dx

:

0r

(c[j

,

1]

-

U,

1l).

Introducing

an

integer

value

s,

to denote

either

* 1

or

-

1,

these six

expressions

can be

reduced

to three

expressions

only.

These

are

rhfi,

1l

-

hlj

-

s,

1])

d-r

hnrs

:

h[j,

1l

r.rr

(rU,

1l-uff-s,

1]) dr

uRts:ugrLl-T

and

dx:

dt

(r[,],

1]

+ scff,

1l)

where

s:

1 is

used

when

the

equations

are

applied

to a

positive characteristic

and

s

:

-

1

when

the equations

are-

applied

to

a negative

characteristic.

Subscript

^R/S

denotes either

subsCript

R or

subscript

S

according

to

whether

s:

L or s

=

-

L'

Then

,-

_h*+

hs

+(u^

* us)cr

-

(F^

-

Fr)ct

nP:-r--T-

u

and

Dp: un

-t

fo"

-

h^)

-

FR

'

It is

quite easy

to write

a subroutine

for a computer

program

which

willperform

these

calculations

systematically,

progressing

through

the

length

of

a

pipe

for

any

given I

Sec. 3.21

The method of characteristics

level

and calculating

the

corresponding

values

at nodes on

the t

+

Lt level.Of

course,

it

will

be

necessary

to

calculate the

values

of

all slowly

varying

parameters before

performing the above

subroutine. Such

slowly

varying

parameters are the

Darcy

/

values

and

the wave speed

c. The

wave

speed

can

vary because

the presence of

air,

or

^-,, ^+L^- -^^ :- +L^ ll^"il ^o- ^Lo--a flra rrrqrra c^aarl .ranr nnncirlarqhlrr

'I-n

Gnrl nrrf

4rry U|lut;r

64D,

ru LttI'/

rrYuru vqlr wrrcrrSw

rlrv wqvv Jlrvvs

tvrJ

vvrroruvr 4vrJ.

f v rrrre

vs!

how

to calculate

these

values, see

p.

139 for the

variation

in

/

and

p.

140

for

the

variation

in c.

There

is one

major

defect

in the method of

the

regular

grid.

This

is

that

the

process

of

interpolation

causes

dispersion

of any

wave that

may be

present. In

Fig.

3.6

the

process of how

and

why

this

happens

is illustrated.

Ax

Fig. 3.6

-

Ar

versus Ar

grid

superimposed

on two

different

types

of

waveform:

R.A,

interpolated

value; RB, RC

wave heights.

Consider

two

waves

passing

through

a Ax

length.

Irrespective

of

their shapes

the

values of

u^ and hp

or

Ds and h5

calculated

by

interpolation

will be the same.

In

effect,

a vertical

wave

front

will be

dispersed

into a

wave of

Ar length, as,

also,

will

any

wave of length

less

than

Ar. This

effect

will not

matter

very

much

if Ax is

a small

fraction

of

the

pipe

length

but,

if the analysis

concerns

a

complex

network,

the

arrival

of long

waves at

junctions

can involve

the superposition

of

wave

shapes,

which have

to be accurately

described

mathematically,

if the

resulting

wave is

also

to

be

represented

with comparable

accuracy.

3.2.3

The

Vardy

method

The standard

method

described

in

the

suffers

from small

Atvalues.

As

stated

above,

the

Ar

value is

given

by

Ar

:

0.95

AxlMax(cr

t ur); so,

when

cr

has

a magnitude

of

1000 m/s,

u,, is

of the order

of

1 m/s

and Ax

is of the order

of

100

m,

then

Ar

will be of the

order

of 0.01

s.

This

will

involve

lengthy

computations

which

might involve correspondingly

lengthy runs

on the

computer.

Vardy suggested

that

by increasing

the

value of

At, say by

a factor

of three,

and

performing interpolations

between

whatever

adjacent

node

points the characteristic

line

origins happen

to

lie

The

method of

characteristics

lch.

3

83

82

vertical-fronted

wave

smooth-fronted

wave

84

The

method of

characteristics

lch.

3

handling

the

boundary

conditions

but

in

the hands

of an expert

analyst

this

presents

no

real difficulty.

In

this method

(Fig.

3.7),

ihe

usual

Ax distances

between

nodes

are employed

but

R'RSS'

|

<----->l+------+

l<----->l

<--->l

<--=>

l+---+l+----+l<-->1

Ax

Fig. 3.7

-The

VardY method.

could

be increased

still

further

but there

is a

risk

that this

might

make

the

P'R'

and

P'.S'

segments

of

the

characteristic

lines so

long

that

they could

not b€

regarded

as

straighiporrions

of

curved

lines.

This is

the factor

which really

decides

how

large

a

Ar

value can be

used in

the

Vardy

method.

Boundary

conditions

4.I

INTRODUCTION

Unsteadiness

cannot

originate

within a

pipe length;

it must

enter

a

pipe

length

either

from

the

upstream

enO

of

the

pipe

or

from

its downstream

end.

It

is

generated

by

hydraulic

devices

connected

ai

these

ends

and

such

devices

are

commonly

called

hydraulic

controls.

Hydraulic

controls

operate

either

by controlling

the

pressure

head

or

the

velocity,

or

by

determining

a relationship

between

the

head

and

velocity

at

the

boundiry

under

consideration.

Some

common

boundaries

are

as

follows:

(a)

Reservoirs.

(b)

Pumps.

(c)

Turbines.

(d)

Valves

of

many

different

sorts.

(e)

Surge

tanks.

(f)

Air

vessels.

(g)

Junctions.

There

can

be

other

types

of

hydraulic

control

of

course

but

the

majority

of

them

fit

into one

or

more

oi

th"

above-listed

categories.

Some

of

these

boundary

conditions

will be

described

in this

chapter

but

some

will be

dealt

with

in

later

chapters.

4.2

RESERVOIRS

Reservoirs

can

be

hydraulic

controls

at

both

upstream

and

downstream

ends

of

a

pipe. They

operate

by

imposing

a fixed

head

at

the end

of

the

pipe.

Let

the

height

of

ihi

watersurface

in

the-reservoir

above

the datum

of

the

system

be

I/....

If

the

reservoir

is located

at the

upstream

end

of

the

pipe,

a negative

characteristic

can

be

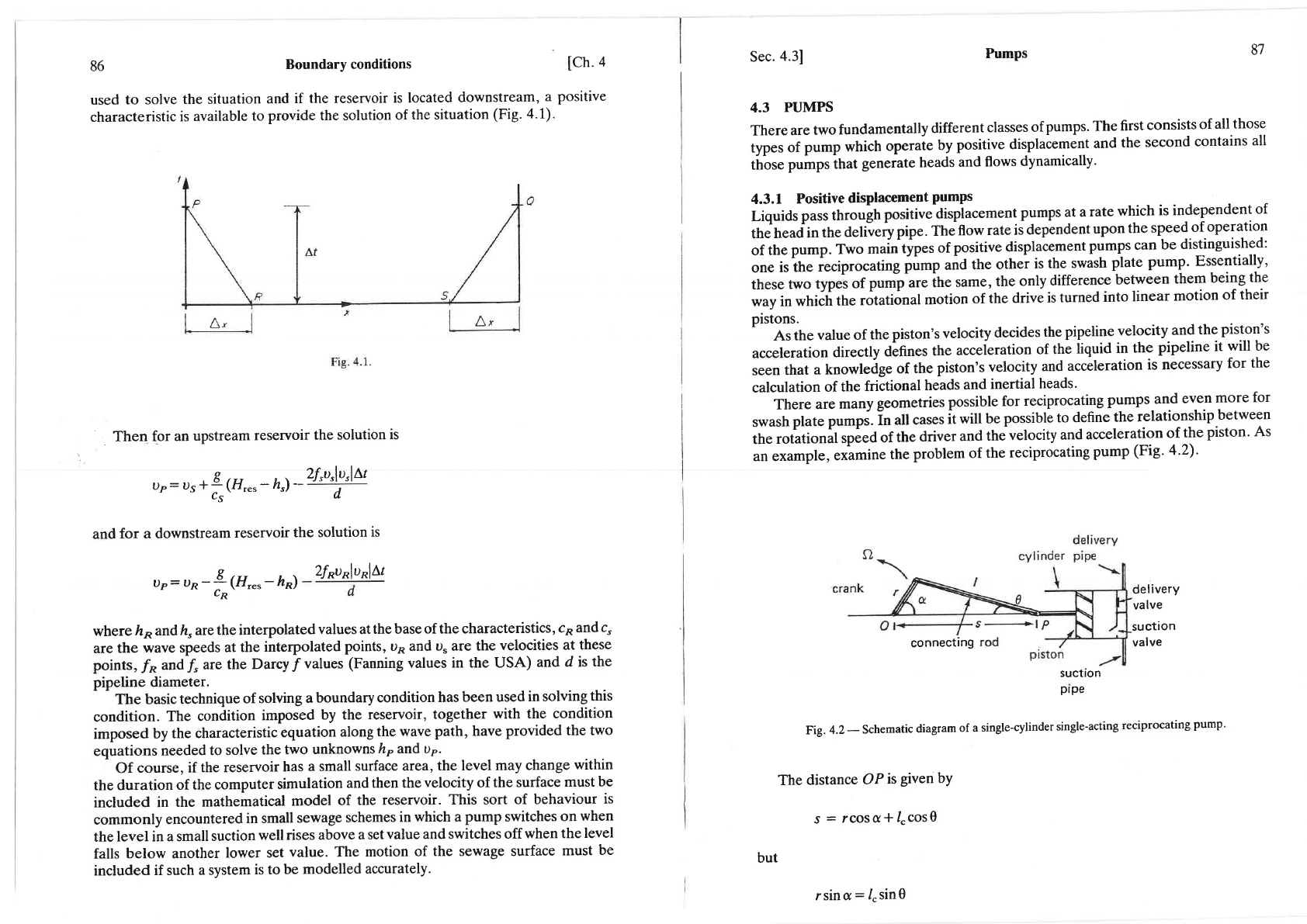
86

Boundary

conditions

used

to solve

the situation

and

if

the reservoir

is located

downstream,

a

characteristic

is

available

to

provide

the solution

of

the situation

(Fig. a.1).

lch.4

positive

Then

for

an

upstream

reservoir

the

solution

is

a 2f,u"lu,lAr

Dr:

us

*

9

(F/..,

-

hrl

-

-'

d

and

for a downstream

reservoir

the

solution

is

t)P:

uR-

fttn,*-

h^)

2f^u^lu^l[t

where

hpandh,aretheinterpolatedvaluesatthebaseofthecharacteristics,cpandc'

are

the

wave

speeds

at

the

interpolated

points, u^ and

Ds are the

velocities

at these

points,

f

*

and

f,

arc

the

Darcy

/

values

(Fanning

values

in the USA)

and

d is

the

pipeline

diameter.

The basic

technique

of

solving

a

boundary

condition

has

been used

in solving

this

condition.

The

condition

imposed

by the reservoir,

together

with the condition

imposed

by

the

characteristic

equation

along

the wave

path,

have

provided the two

equations

needed

to solve

the

two

unknowns

h, and u"-

Of

course,

if

the reservoir

has

a small

surface

area,

the level

may change

within

the

duration

of the

computer

simulation

and

then the

velocity

of

the surface

must

be

included

in

the mathematical

model

of

the

reservoir.

This sort

of behaviour

is

commonly

encountered

in small

sewage

schemes

in

which a

pump

switches

on

when

the

level in

a small

suction

well rises

above

a setvalue

and switches

off

when

the

level

falls

below another

lower set

value.

The

motion

of

the sewage surface

must

be

included

if such

a system

is to

be modelled

accurately.

Pumps

87

4.3

PUMPS

There

are

two

fundamentally

different

classes

of

pumps. The

first

consists

of all

those

types

of

pump

which

op"rui"

by

positive

displacement

and

the

second

contains

all

tirbse

pumps that

generate

heads

and

flows

dynamically'

4.3.1

Positive

displacement

pumps

Liquids

pass throuih

positive

dispiacement

pumps

at a

rate

which

is

independent

of

the

head

in

the

deli"very

pipe. The

flow

rate

iJ

dependent

upon

the

speed.of

operation

of the

pump.

1*o

rnuin

types

of

positive

displaiement

pumps

can

be

distinguished:

one

is

ttre

ieciprocating

pu*p

und

ttt"

othei

is

the swash

plate

pumP'

Essentially'

these

fwo

typei

of

pum-p^ar"

ih"

same,

the

only

difference

between

them

being

the

way

in

whiih

the

rotational

motion

of the

drive

is

turned

into

linear

motion

of

their

pistons.

As

the

value of

the

piston's

velocity

decides

the

pipeline

velocity

and

the

piston's

acceleration

directly

defines

the

acceieration

of

the

liquid

in

the

pipeline

it

will be

seen

that

a knowleige

of

the

piston's

velocity

and

acceleration

is necessary

for

the

calculation

of

the

frictional

heads

and

inertial

heads'

There

are

many

geometries

possible

for

reciprocating

pumps-and

even

more

for

swash

plate

po-pr.

in

all cases

ii

will

be

possible

to

define

the

relationship

between

the

rotationit

spieO

of

the

driver

and

the

velocity

and

acceleration

of

the

piston'

As

an example,

eximine

the

problem

of

the

reciprocating

pump

(Fig. a.2).

Sec.

4.31

delivery

valve

suction

valve

suctron

ptpe

Fig.

4.2-

Schematic

diagram

of a

single-cylinder

single-acting

reciprocating

pump'

The

distance

OP

is

given bY

s

:

rcosc*/"cos0

connecting

but

rsins:/.sin0

88

cos2e-1-sin20

therefore

Boundary

conditions

lch.

4

r:rcos

u*t,J(t

-

(;)'

,into)

but

ds/dr:

Dpistoni s0

(

|

(;)','"'"]-"(i)'$"e")L]',

Dpiston:t-rsins-tLt-

Given

the

value of

s

(say

r

+ l)at

a time

t

(say

t

:

0)

then a

will

be

zero.

Assuming

these conditions

as

a start

point,

the

values of u can

be calculated

for successive

Al

values.

a

will increase

according

to the

finite

difference equation

o::

or+

QAI

times.

The relationship

between

the

piston's

velocity upiston

and the

velocity up

in the

pipeline

is obtained

from

the

continuity

equation.

It

is

simply

Api,to,,

upiston

:

Apip"

up(l

-

o)

where o

is

the slip over

the

piston:

volume

swept

out

by

piston

-

volume

delivered

o=

.

The

volume

swept

out

by

the

piston

does

not

(quite)

equal

the

volume delivered

per

stroke

because

of

leakage

back

over the

piston.

This leakage

is commonly

called

slip

and

it is usually expressed

as

a fraction

of

the swept

volume. There

is

another

small

error

which,

so

far,

has

been

ignored

and this is

a consequence

of

the

compressibility

|

-

w(hoownsrream

-

fr,,o.,r."*)/K

where

K is the bulk

modulus

of

the liquid.

In

most

circumstances this

multiplier

is

very nearly

equal

to unity.

The

values

of /too*.stream

and

lz.,o.,ream

can

be

taken

at

the

current

time

level and

so

have already

been

calculated and hence

are available.

Sec.

4.31

Pumps

89

If

gases are

being

pumped,

as in blowers

for car engines,

the

essential

technique

is

the

same

but

the

uatiiUt.

that

is conserved

across

the

pump is

the mass

being

pumped

per stroke.

A

gas

process

must

be selected

-

adiabatic,

isothermal

or

polytropic

-

and

this

will enable

the

calculation

of

gas

compressibility

to be

performed.

heads

upstream

and

downstream

of

the

pump can

be

calculated.

4.3.2

Swash

plate

pumps

In

a similar

fashion

tb that

that

was used

for

reciprocating

pumps, the

velocities

of

the

driving

device.

A

word of

warning

about

positive displacement

pumps is appropriate

at

this

point.

Positive

displacernent

pumps must

not

be

equipped

with

a shut-off

valve of

any

Boundary

conditions

lch.

4

sort

unless

a

pressure

relief

valve

upstream

of it

and downstream

of

the

pump

has

been fitted.

This type of

pump

will

continue

to

deliver

flow irrespective

of

the

resistance

of the

pipe

network

as such flows

are

dependent

only

upon the

rotational

speed

of the

pump and not upon the

valve's

setting.

Either such

pumps

will burst

their

associated

pipework

or

their

motors

will be stalled,

with

consequent

risk

of

burn-out

due

to the excessively

high

torques

presented to them if downstream

valves

are closed.

Electric motors

driving

positive displacement

pumps

should

be equipped

with

therrnal

trips or

some

other

cut-out

device

and the

pump

should

have a

burst

disc

or

pressure relief

valve

fitted

on

the delivery

side.

Great

care should

be

taken

in

choosing their

rotational speed

because,

unless they

have

a

sufficiently

large

number

of cylinders,

high rotational

speeds

will

generate big transients

in

the

pipework at

every

rotation with consequent

risk of bursting.

Single

acting cylinders

are more

prone

to

this than are

double

acting

cylinders.

It is

recommended

that

all

schemes

using

positive

displacementpumps

should

be analysed

before

installation,

especially

if the

pump

has

few cylinders

or

if these cylinders

are of single

acting type.

Because of

the risk of rupturing

the

pipework

of any scheme

driven

by

positive

displacement

machines it is usual

to

fit air

vessels on both

sides of such

machines.

The sizing

of such

air

vessels has been

carried

out

in the

past

using

approximate

methods

and

experience. On

the

whole

they

work well, but now

their analysis

can

be undertaken

using

the

theoretical

approaches

given

in this

book

(see pp.

1l+120);

it

is

suggested

that

the

pump, its associated

air

vessels

and

the

pipe

network

should

be analysed

and

its

safety

properly

established.

4.3.3 Rotodynamicpumps

Most

pumps

in

use today

are

of the rotodynamic

type. The

word rotodynamic

means

that the

pump

generates the

flow through

it and the

head across

it

by the

dynamic

effects

that

it applies

to

the

liquid being

pumped.

Such

pumps

fall

in to

four

categories:

(a)

Radial

flow

pumps.

(b)

Mixed

flow

pumps.

(c)

Axial

flow

pumps.

(d)

Turbo

pumps.

It is

not the

intention

to

give

a

detailed

description

of how

pumps

operate

and it

will be assumed

that

the

reader is conversant

with

the

basic theory

of

rotodynamic

machinery.

This basic

theory

is

taught on mechanical

engineering

courses

and

on

some civil

engineering

courses;

most textbooks

include

the

material.

The

author's

book An

introduction

to engineering

fluid

mechanics'

published by

Macmillan

includes all the

material

required

for this

section.

To describe the

relationship

between the

rotational speed

of

a

pump,

the

flow

through

it and

the

head

across

it, an equation

relating these

three

variables

is

required.

Such

an equation

can

be used

in conjunction

with

the

appropriate

characteristic

invariant

to

obtain

the

velocities and heads

upstream

and downstream

of the

pump.

Thus

a solution

will be obtained.

The

problem

remains

that

a

pump is

Sec.

4.31

Pumps

on

whether

the

variables

are

positive

or

negative'

Figs.

4.3 and

4.4

are

typicil

of four

quadrant

characteristic

curves

of

a rotodyna-

lorque

heod

/)

zone

DZ

fve

lorqu(

rve

neoo

normol

pumplng

+

ve

torque

+ve heod

\

+ve

lorque

-

ve

heocl

-

ve

torque

-ve

heod

91

90

Positive lorgue,posrlive

heod.

positive /y' ond

posifive

Q

ore

oll

os

fOr

normol

PumPing

Fig.

4.3

-

Pump

characteristic

zones.

92

Boundary

conditions

lch.4

4

Fig.

4.4

-

Pump characteristics.

QlQ"

.

On such a system

of coordinates,

lines of constant HIH* and

lines

of

constant

TIT*

are plotted. Note

that

steady

state

values

Q*,

H*, and ?o are the flow at

the

pump's

duty

point

when

running at

the

steady state

speed, the head at this

point

and

the torque

exerted

on

the

pump

at this

point,

N* being the steady running speed

usually in

revolutions

per

minute.

In Fig.

4.4 the complete

characteristic curves

of a

pump

are illustrated.

Note the

four straight

lines 01,02,03

and 04;these

lines delineate the boundaries of

the eight

zones into which

the

whole diagram

divides

(see

Fig.

4.3).

In Fig.

4.3 the

eight

sectors

alone

are

shown.

The normal

steady

state operating conditions of the

pump

lie on a

horizontal line through

N/N*

:

L.

The zones

of

operation

of

the

pump

lie between

the lines

and

are

variously

labelled

P, T

or D

with a number. P denotes a

pumping

mode of

operation,

Idenotes

a

turbine

mode

and

D denotes

a

dynamometer mode.

It is

very

unusual for

a

pump

to enter the

fourth

quadrant.

Sec.4.6l

Dynamometer

operation

4.4

PUMPING

OPERATION

4.4.1

The Pl

zone

In normal

pumping

operations

the

pump

w9r\s

in

the

P1-. zone.In

steady

state,

N

equals

N* ind

p

equats

O*;

so

N/N*

:

1

and

QIQ*

:

1. The

steady

state

operating

point

thus

lies on

ttt" extreme

right-hand

edge

of the

zone

at

the

point where

the

graph

coordinates

are

1,

I but

when

the

pump is

running

in

unsteady

conditions

the

6perating

point will

lie

off

the

45'line

in the

space

between

the ordinate

through

the

origin

unl

tfr" 45'line.

In this

space

the

head

across

the

pump will be

positive,

i.e the

deilvery

head

will

be

greater than

the suction

head; the

flow

will be

positive,

i.e.

the

flow

wiil

be

in

the

forward

pumping

direction;

the torque

applied

to the

pump

will be

in the

positive direction,

i.e.

the

motor

will be driving

the

pump.

4.4.2

The

EL znlne

It

will be

realized

that,

if a

pump

is run

backwards

at

an appropriate

speed

driven

by

a

negative

torque,

it

wilt spin

the

contents

of

its casing

so

as to

generate a forced

vortex

wit-trin

it. ftris

produces

a

positive

head

and small

positive flows

can

then

be

delivered.

fire

pump

operates

as

a

pump, although

with

low efficiency-hence

the

Y2zone.It

is

very rare

for a

pump to operate

in

this

zone'

however-

4.5

TT,JRBINING

OPERATION

4.5.1

The

Tl zone

When

a

pump is

switched

off,

for

a short

time

flow

will continue

in

the

pipeline

and

it

often

trappens

that

such

a

flow

has enough

momentum

to enable

it to

drive

the

pump

in a

forward

direction,

causing

it

to supply

energy

to the

motor

and

pump

set

which

in

turn causes

it

to speed

up and

to

extend

its

run-down

of speed

greatly.

This

has

very

considerable

impiications

concerning

pipeline safety

which

are

discussed

later

in the

book.

This

is

?"1

mode

operation

and

itis sometimes

called

forward

turbining-

It is

very important

to

be

abie

to

predict forwaid

turbining

accurately

because,

if the

posiUitity of

it is

not

includedin

the

analysis,

transients

of

large

magnitude

will be

predicted which

do

not,

in fact

occur

in

reality.

4.5.2

The

?ll zone

Radial

flow

pumps resemble

turbines

very

much.

In

some

pumps

the

resemblance

is

so

great that the

putttp

can

be

reversed

and operated

as

a turbine.

An

example

of

this

o.Jurr

in any

pu*p"d

storage

scheme

such

as

the

Dinonric

scheme.

The

zone of

flow

and speed

nltu.s

in

which

this

happens

is

called

the

TLzone.

Provided

that

no

non-

return

valve

is

fitted,

any

pump can

operate

in

this

zone.

4.6 DYNAMOMETEROPERATION

There

are

four

zones

in

which

a

pump

can

operate

as

a dynamometer,

dissipating

energy

rather

than

converting

the

rotational

energy

of the

motor

into

potential

or

pressure

head

as does

a

normal

pump.

4.6.1

Zone

Dl

Normally

the

piPe

will

be

a

rising

93

Consider

a

pump delivering

a flow

to

a

reservoir.

94

Boundary conditions

lch.

4

reservoir.

The

pump will be operating

as

a

pump and

will

be in zone

Pl

(the first

pump

zone).

If, for

some

reason,

the level in

the

downstream

reservoir is

lowered,

the

pump

flow

will

become

larger and larger

as

the

head

against

which the

pump

is

working diminishes.

Eventually

the head

will become

negative

and this

will happen

as

the

downstream

reservoir

level

falls

below

that

in the

upstream reservoir.

The

energy

that

the

pump

is

then

supplying

to

the

water

is still

given

by wQHbut

now fl

is

negative.

In

effect

the

pump is

generating

a negative

quantity

of energy,

i.e.

it

is

destroying

energy

even though

the

motor

is still

running

and driving

the

pump at its

steady

running

speed.

The

pump is thus

acting

as

a dynamometer.

This

corresponds

to the first

dynamometer

mode:

Dl.

For

another example

consider

the case

of

two

booster

pumps

in series on

a

pipeline.

The

upstream

pump

may be

forcing

water

through

the downstream

pump so

that

it starts

to

generate a negative

head

and so

starts to

act

as a dynamometer.

Again,

this

is an example

of

Dl, zone

dynamometer

mode

operation.

4.6.2 The

D2

zone

If

a

pump, running

at a

positive speed,

experiences

a delivery

head

which

is

larger

than its delivery

no-flow

head,

and it does

not

have a non-return

valve fitted,

flow

will

be

forced

backwards

through

the

purnp.

The

torque

will be

positive,

the

head

will be

positive, but the

flow

will be

negative.

The head

in the

delivery

pipe will be

large

but

the head

in

the suction

pipe will be

very much

smaller.

The

pump

therefore

must

be

destroying

energy

and so

must

be acting

as a dynamometer.

This

is the

D2

zone.

4.6.3

The

D3 zone

In

the

third

quadrant,

another

dynamometer

zone exists.

In this

quadrant the

pump

is

running

backwards

and

the

flow is

reversed.

The head

in the delivery

pipe

is

higher

pump

then

exhibits.

4.6.4

The

D4 zone

The D4

zone is

in the

fourth

quadrant.

It is most

unlikely

that a

pump will ever enter

this zone

as

it is

most

unusual

for

any

pump

to enter

the

fourth

quadrant.

In the

fourth

quadrant,

the

direction

of the

impeller's

rotational

motion

is in

the reverse

direction

as are the

torque

and

head.

The flow

is

in

the

positive

direction.

The fourth

quadrant

is made

up

of the

F2 zone

and

the D4 zone.

As stated

before,

the

impeller

can

act as

a

pump

even

when rotated

in the reverse

direction

but, if

flows

become

relatively

large, the

head that

the

pump

can

generate

decreases

due to friction

losses

and

eventually

bemmes negative. Once

this happens,

Sec.

4.71

The

Suter

presentation

representation

of such

a complete

set

of

pump characteristics

which

is ideally

suited

to a

computer

solution

using

the

method

of

characteristics.

The

following

presen-

tation

is taken

from

Suter's

original

papar.

4.7

THE SUTER

PRESENTATION

There

are

many

ways

of

presenting

the

curves

of

a

pump

operating

in

four

quadrant

modes.

If

dimensional

analysis

of

rotodynamic

machines

is

performed,

the following

result

can

be

obtained:

95

*(*,,,#

PND,

p)

k

D

u)

:o

The

first

group really

represents

the

ratio

u{u,thesecond

represents

the

ratio

ulu,the

third is

the

Reynold;s

nimber,

the

fourth

is

the

roughness

number

and

the

fifth

is

the

efficiency.

urii

the

denotes

velocity

of

flow,

u is

the absolute

velocity,

rz is is

the

speed

of the

blade

tip

and

E is

the

pump's

efficiency.

In

a

pump, Reynolds'

numberis

large

and

variations

in its

value

have

little effect

on the

nature

of

the

flow

through

the

impeller.

klD

is

usually

very small

as

the

inner

surfaces

of

pumps are

finished

io high

standards

and often

with

a

high

polish; so

the

precise

value of'klD

is

not

importani.

Then

the

function

can

be

reduced

to

a function

ielating

three

variables

only:

Q\ND3,

gHlN2D2

and

E. The

function

is really

a

statement

that

the efficiency

depends

on

the

geometry

of

the exit

velocity

triangle

of

the

pump. In

effect

this

means

that

the

behaviour

of

the

pump depends

on only

two

parametl

rs-

elND3

and

the

blade

angle

-

as this

is sufficient

to

define

the

velocity

iriangle

for

any

given

pump.

Actually,

QIND3

is

merely

another

way of

writing

elribuwhichis-u7a

as

statid

previously;

b

is

the

breadth

of

the

impeller

at

exit;

D

urrd ,

are

as definiO

previously.

In

an

individual

pump, the

ratio

reduces

to

QIN

because

D is

a

consiant

for

any

given

pump. Similarly

a torque

group can

be

formulated.

The

power of

the

pumP is

wQnn;

so,

multiplying

the

three

groups

and

p/p

togetner

([tNOz)(BHNzDIE(plp)

grves PlpN3DsE

which

is the

shape

numbei.

Dividing

P byd,

the

angular

neiociiy,

gives the

torque

so

TtpNzDs

gives

a

torque

group:

TlNz

asiuming

that

the

mass

density

p

and

the

diametet

D

is constant-

Q

can

U!

tatln

either

as

p/N-or

as

QlrDbu,

\,

can

be taken

as HlN2

or

asLgHluz

and

1.

can

be

taken

asTlNz

or

as

4TlrpDzba2.

Suter

suggests

that,

to

avoid

infinities

and

a

presentation

that

would

contain

multiple

values

for one

value

of

the

independent

variable,

two

dependent

variables

W,

and

W,

be

introduced.

The

dependent

variable

4

specifies

the

value

of

ry

(the

head

group)

in terms

of

.th-e-

$

(the flow

group)

anOttri

variable

I7,

does

the

same

for

l.

(the

torque

grgup)t

Note

that

the

Lrp"ir.tipt

asterisk

(*)

denotes

that

the

variable

to

which

it is

applied

is a steady

state

operating

point

value.

Then

wn:sign(rr)

lffi

Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

Подождите немного. Документ загружается.