Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

56

The

Allievi interlocking

equations

and

graphical

methods

[Ch.

2

An exactly similar analysis

can

be

performed

for an observer travelling

down-

stream

and the following result

will

be obtained:

h*,r-

h,,,:

-

i(rr,

r-

u,.,).

I

So

a general result emerges

which is that for

waves rnoving up and

down

pipelines

h*.r-

h,,r:

!l@*.r-

u,.,).

5

The

positive

sign

applies to a

wave

moving

upstream against the flow and

the

negative

sign

applies to

waves moving downstream

in the direction

of the flow.

The two equations

above

need further modification because heads are related

to

velocities

in them and it is

required that heads should

be

related to flows. To

achieve

this merely

multiply the top and bottom of

the right-hand side by the area of the

pipe,

Thus

,

h*.r- h,.,: xL*@x,r-

e,,,).

These

equations

are the equations

of two

straight

lines

but only apply

for

an

observer

travelliug either

upstream

or

downstream at

wave

speed.

Fig.2.4

-

The

waterhammer

or eagre lines.

Line I in Fig.

2.4

applies

to

waves travelling upstream and line II to

waves

travelling downstrbam.

The concept

underlying these two lines is that of two

observers travelling in opposite

directions

at

the

wave

speed c m/s.

These observers

-

or waveriders

-

see

waves

propagating

in the directions in which they

are

going

as

being

of

unchanging

magnitude

and these

magnitudes

A,Fl are proportional

to

the

flow

fluctuations

that

generated

them.

The

only difference

between

them is that,

in

Sec.2.1l

Analytic

methods

the case

of the observer

travelling

alongside a wave moving downstream,

an

increment

in flow causes

a decrement

in head

(a

negative

wave)

but, in the case

of the

observer travelling

upstream, an

increment in flow causes an increment in

head.

These

lines are sometimes

called

waterhammer lines and sometimes eagre

lines.

'l-he

rwnrrl ArorF ic

qn

nlrcnlccnenf rvnrrl rwhir-h rlesnrihec c srnlll u/qwp frawellino nn a

lrrv

tlvrs

vq6^v

r9

str vvuv

free surface

flow. It

is rarely used

nowadays in its original meaning

which one

supposes

is the

reason

that it is so suitable for its new

use.

Head

values

are

required together

with

those

of

the

associated flows and

these

pairs

of

values are required

at locations

along the

pipeline

and at

various times,

i.e.

there

are four

variables

present.

Usually,

if one is developing

a

graphical

presen-

tation, one needs

one dimension

per

variable but this cannot be achieved

when one

is

trying to describe

the

variation of four

variables

on

paper.

To describe

the

way

in

which the four

variables

interact,

the concept of

the

waverider is introduced.

The

waverider can be thought of as an observer

riding

on

the

wave. He

will travel at

the speed of

the

wave

and his

position

in the

pipeline will

be

related to

time. In

this

way a

point

on an

ft versus

q plot

can represent

both

position and time,

and so the

problem

of

representing the four

variables

of.

h,

q

,x

and

t

can

be resolved.

The

author regards

this

particular

device

as especially

clever

and

feels

that the inventors

of it

must have

been correspondingly intelligent.

2,4.2

Putting the three

ideas together

Take the

case of

a

simple

pipe with a reservoir B at its

upstream end and

a slowly

closing

valve A located

at its

downstream end.

Any

pressure wave

that occurs

in

the

pipeline travels

either

upstream

or downstream

at a

speed

of c m/s.

It will take

a time

of.ZLlcto

pass

up

and back

down

the

pipe,

i.e. a time of

T, which is the

pipe

period.

InFig.2.5,timeswillbedenotedbymultiplesof

T(e.g.

l.5DasasubscriptofA

orB,

and, for convenience,

only the

multiple

will be shown in subsequent

diagrams,

the

value T being omitted.

Referring

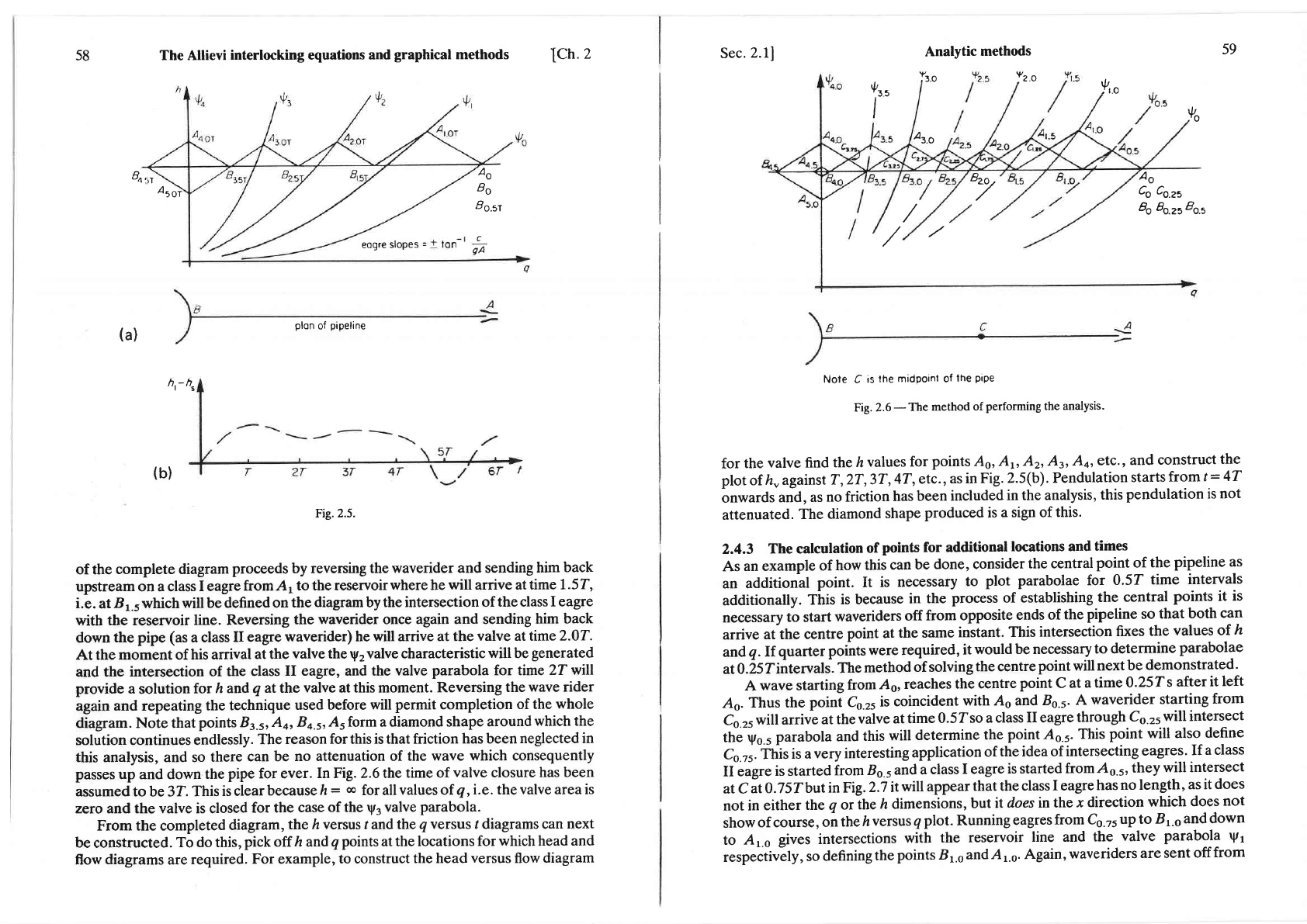
to Fig. 2.5,

the

points

As and

Bo refer

to

steady

state

which

was the condition

before

the

valve

started

to

close. Steady

state

is

defined

atAswhere

the

rys

parabola

intersects

the

horizontal reservoir

line.

At

this

point

the

ordinate of

the

parabola is equal

to the reservoir

head

(remember

that friction

is

negligible)

and when

this happens

the head loss

though the

valve

equals

the

applied

head

and the

flow at

the reservoir

end of

the

pipeline

equals

that at the

valve.

This, of

course,

defines steady

state.

Now,

as there

is no friction

in the

pipeline,

the head at Ao must be the

same

as that

at the

reservoir

up until

the time

at

which

the

first

wave

arrives

from the

valve, i.e.

up

until 0.5

xZLlc

or

0.5L So

Ao

is coincident

with Bo.r. At this

point

it should

be

realizedthat

by

the use of

/ and

B we are defining the

locations of

two

points

on

the

pipeline

-

we have considered

r variation

-

and by the

use of the subscripts

we have

defined

various times

-

we have considered

r

variation. We have specified

h,

q

,

x

and

/ for

two

points

in space

and time.

In other

words, we have fulfilled the

requirement

of defining

the

values

of

four

variables. Next,

imagine a

waverider

starting

from

the

reservoir end

at time

0.5Tand

travelling

downstream

to the

valve. When

he arrives,

he

will be at A at time

Zand

he will have

travelled

on a class II eagre

line,

i.e. one

of

negative slope.

At

time Zthe

ry,

parabola will

suddenly

appear to

the waverider

and

he

will find himself

to

be both on

the eagre

line and also on the

ry, parabola. This

will

define

the

pointA,

completely.

The

process

can

be

seen

on

Fig. 2.5. The construction

57

s8 The Allievi

interlocking equations

and

graphical

methods

ICh.2

8nT

Bo

r'roi

Bo.st

eogre

slopes

C

9A

hr- h,

Fig.2.5.

of the

complete diagram

proceeds by reversing

the

waverider and sending

him

back

upstream on a class

I eagre

from A

1

to the reservoir

where he

will

arrive

at time

I.5T

,

i.e.

at

81.5 which

will be defined

on

the

diagram

by

the intersection of

the class

I eagre

with

the reservoir line.

Reversing

the

waverider

once

again and sending

him

back

down

the

pipe

(as

a class

II eagre

waverider) he

will

arrive

at the

valve at time

2.07.

At the

moment of his

arrival

at the

valve the

ry,

valve characteristic

will

be

generated

and the

intersection

of the

class

II eagre, and the

valve

parabola

for time

2T

wlll

provide

a

solution

for

h and

q

atthe

valve at this moment.

Reversing

the

wave rider

again

and repeating

the technique

used

before

will

perrnit

completion

of the

whole

diagram. Note that

points Bs.s,

Ao, Bo.s,A,

form a diamond shape

around

which the

solution continues endlessly.

The

reason

for

this

is that friction

has been

neglected in

this analysis, and so

there

can be

no attenuation of

the

wave

which

consequently

passes

up and down

the

pipe

for ever.

In Fig. 2.6the

time of

valve

closure

has been

assumed to be 3I.

This

is clearbecause

h=

q

forallvaluesof

q,

i.e. the

valve

area

is

zero and the valve is closed

for the

case

of the

ry3 valve

parabola.

From the completed

diagram,

the ft

versus t

and

the

q

versus / diagrams can

constructed.

To do this,

pick

off ft and

q

points

at the locations

for which head

and

flow

diagrams

are

required.

For example,

to construct

the head

versus

flow

diagram

(a)

(b)

plon

of

pipeline

9.,

/

Sec.

2.11

Analytic

methods

Y.^

At.o

Ao

co co.zs

8o Bo.zs9o.s

Fig.2.6

-

The

method

of

performing the

analysis.

for

the

valve find

the ft

values

for

points Ao, Ar,

Az, Az,

A4,

etc.,

and

construct

the

plot

of

ft., against

T,2T,3T,4T,etc.,

as in Fig.

2.5(b).

Pendulation

starts

from

t:47

-onwards

and,

as

no friction

has

been

included

in the analysis,

this

pendulation

is

not

attenuated.

The

diamond

shape

produced is

a sign of

this.

2.4.3

The calculation

of

points

for additional

locations and

times

As

an example

of

how

this

can

be

done, consider

the central

point

of

the

pipeline

as

an

additionll

point. It

is

necessary

to

plot parabolae for

0.5T

time

intervals

additionally.

This

is because

in the

process of

establishing

the

central

points it

is

necessary

to start

waveriders

off

from opposite

ends

of

the

pipeline so

that

both

can

arrive

at the

centre

point at

the same

instant.

This

intersection

fixes

the

values of

ft

and

q.If

quarter

points

were required,

it

would

be necessary

to determine

parabolae

at0.r5Ti;tervals.

The

method

of solving

the centre

point

will

demonstrated.

A

wave starting

from

Ao,

reaches

the

centre

point

C

at

a time

0.25Ts

after it

left

As.

Thus the

point

Cs.25

is

coincident

with As and

Bo.r.

A

waverider

starting

from

Cs

,5

will arriv-e

at the

valve

at

time

0.5lso

a class

II eagre

through

Co.rr

will

intersect

th;

t'.s

parabola and

this

will

determine

the

point Ao.r.

This

point

will

also define

Cs.rr.

This

is

a

very interesting

application

of

the idea of

intersecting

eagres.

If

a class

II eigre

is started

from

Be.5

and

a

class

I

eagre

is started

from46.r,

they

will

intersect

at Citg.75lbut

in Fig.

2.7 itwill

appear

that the class

I

eagre

has

no length,

as it

does

not in

either

the

q

or

the

ft

dimensions,

but

it

does in the.r

direction

which

does

not

show

of course,

on

the

ft

versus

q

plot.

Running

eagres

from Cs.75

up to

Bt.o

and down

to

^Ar.o

gives intersections

with

the

reservoir

line and

the

valve

parabola

y1

r"rp"Ciiroily,

so

defining

the

points Br.o

and

Ar.o. Again,

waveriders

are sent

off

from

59

Yz.o

9'.o

Yo

'z

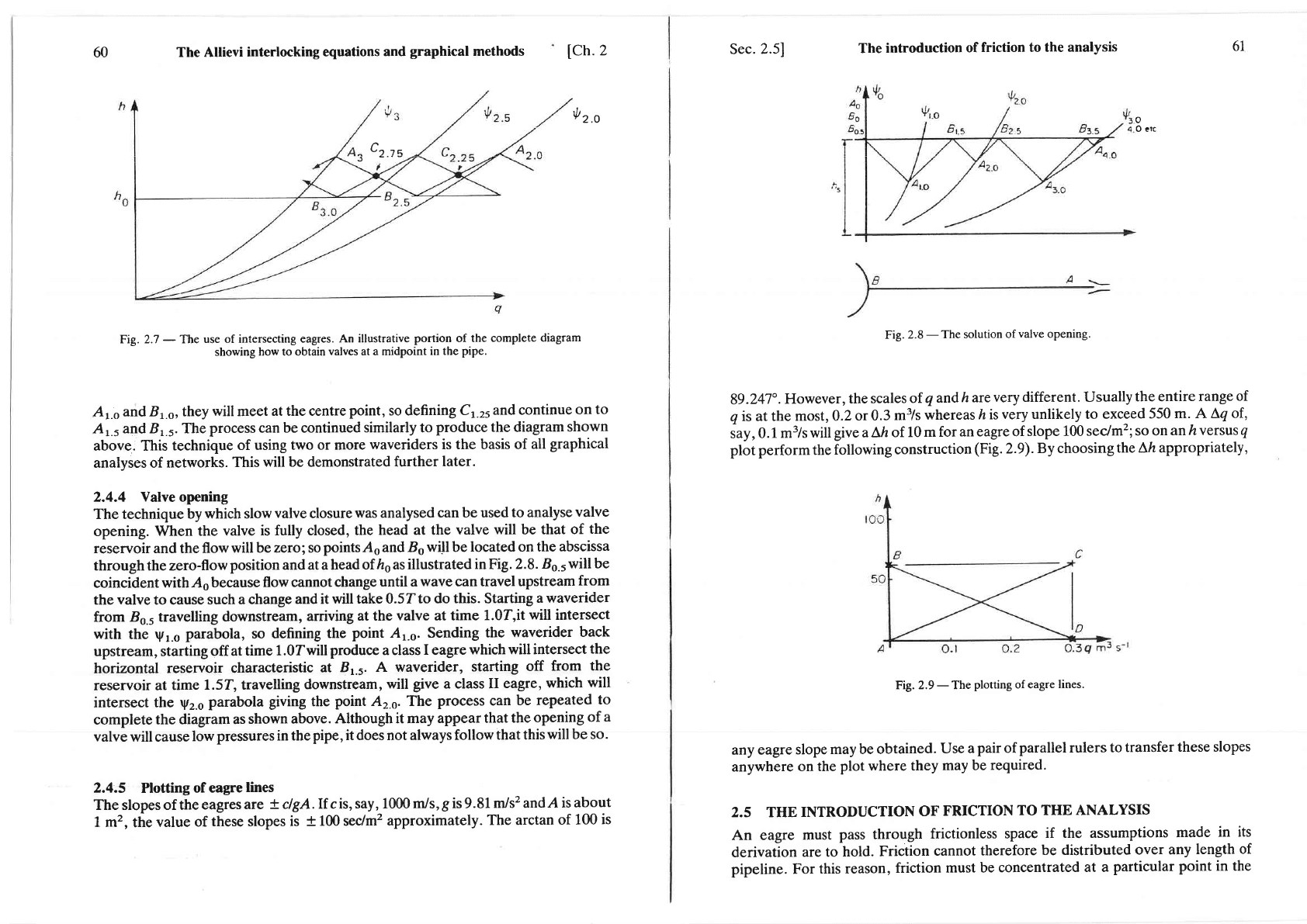
Nole

C

is

the

midpoinl of

the

PiPe

60

The Allievi

interlocking

equations

and

graphical

methods

lch.

2

0

r.o

Fig. 2.7

-

The

use of intersecting

eagres.

An illustrative

portion

of the

complete

diagram

showing

how to obtain

valves at a midpoint

in the

pipe.

Ar.o

and Br.o, they

will

meet

at the centre

point,

so definingCr.zsand

continue

on

to

A,

,

and Br.r. The

process can be continued

similarly to

produce

the diagram

shown

above. This

technique

of using

two or more

waveriders is the basis of

all

graphical

analyses of networks.

This

will be demonstrated

further

later.

2.4.4

Valve opening

The technique

by

which slow

valve

closure

was analysed

can be used

to analyse

valve

opening.

When the

valve

is fully closed,

the head

at the

valve

will

be

that of

the

reservoir and the

flow

will be zero;so

points

Ao and .Bo

will be

located on the

abscissa

through the zero-flow

position and at a head

of &s as illustrated

in

Fig.

2.8.

Bo.swill

be

coincident

with,Ao

because

flow cannot

change

until a

wave can travel upstream

from

the

valve

to cause

such a

change

and it

will take 0.5Tto

do this. Starting

a waverider

from

Bo., travelling

downstream,

aniving

at the

valve at time

L.0f,it

will

intersect

with

the

ryr.s

parabola,

so defining

the

point

Ar.o.Sending

the

waverider

back

upstream, starting

off at

time

l.0Twill

produce

a class

I

eagre

which

will intersect

the

horizontal

reservoir

characteristic

at

81.s.

A waverider,

starting

off

frorn

the

reservoir at

time

1.57, travelling

downstream,

will

give

a class II

eagre,

which

will

intersect the

ry2.s

parabola

giving

the

point

Ar.o. The

process

can

be

repeated

to

complete

the diagram

as

shown

above.

Although it may

appear that

the

opening

of

a

valve

will cause

low

pressures in the

pipe,

it does not always

follow

that this

will be so.

2.4.5

Plotting

of eagre

lines

Theslopesof theeagresare

*

clgA.Ifcis,say,

1000m/s,Bis9.81m/s2andAisabout

1m',

the

value

of

these slopes

is

+

100 sec/m2

approximately.

The arctan

of

100

is

cr.,

u

Sec.

2.51

The

introduction

of

friction to the

analysis

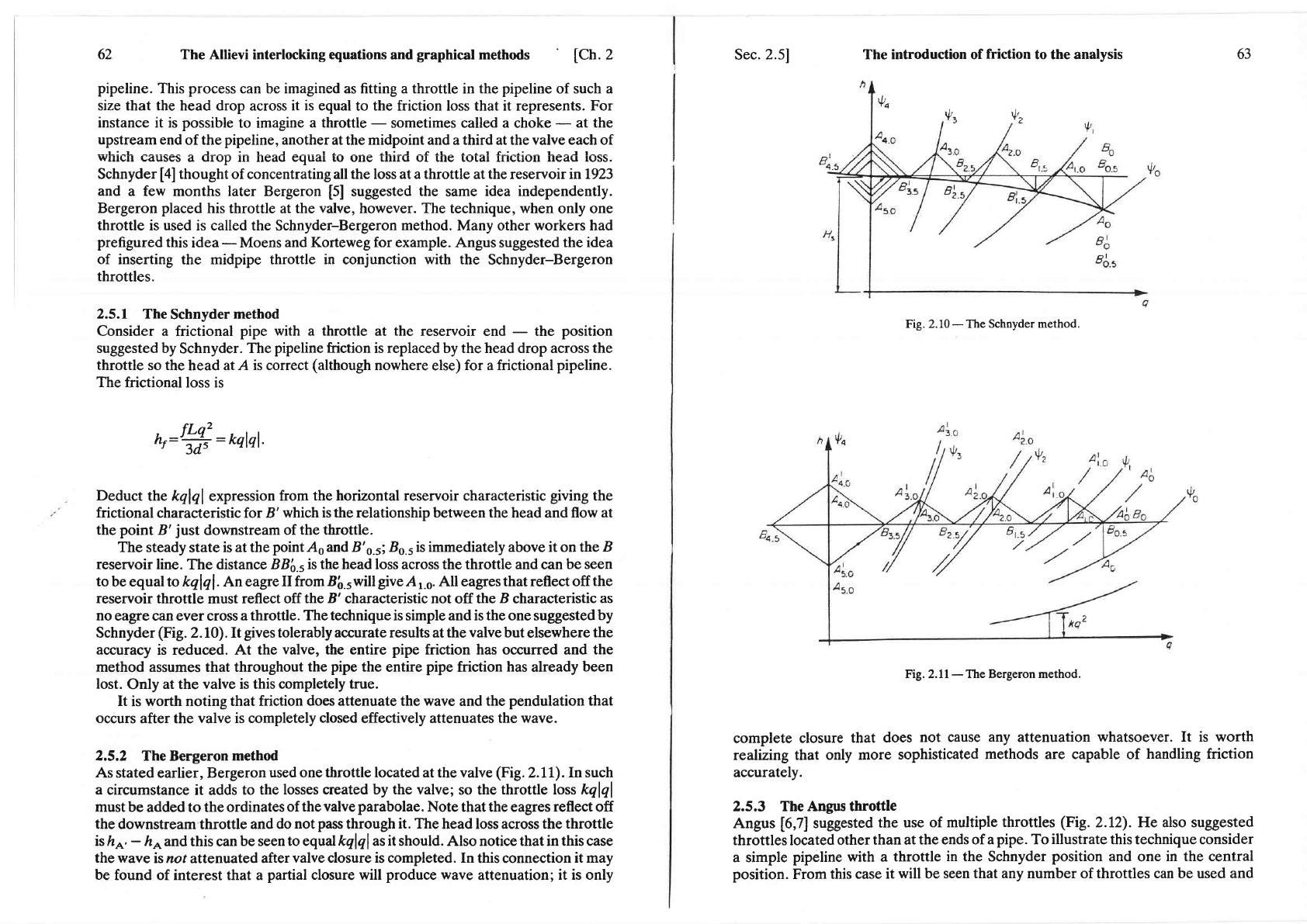
Fig.

2.8

-

The solution

of

valve

opening.

89.247".However,thescales

of.qandharcverydifferent.Usuallytheentirerangeof

q

is atthe

most, 0.2

or 0.3

m3/s

whereas

/r is

very unlikely to

exceed

550

m. A Ag

of,

Jay,

0.1

m3/s

will

give a Lh of.1,0

m for

an eagre of

slope 100

sec/m2;

so on

an h

versus

q

plot perform the

following

construction

(Fig.

2.9).By

choosing

the A/r appropriately,

Fig.2.9

-

The

plotting

of eagre

lines.

any

eagre

slope

may be obtained.

Use

a

pair

of

parallel

rulers

to

transfer

these slopes

anywhere

on the

plot where they

may be

required.

2.5 THE

INTRODUCTION

OF

FRICTION

TO THE ANALYSIS

An eagre

must

pass through

frictionless

space

if the assumptions

made

in

its

derivation

are to

hold.

Friction

cannot

therefore

be distributed

over

any

length of

pipeline. For

this reason,

friction

must be

concentrated

at a

particular

point in the

61

o

O erc

62 The Allievi

interlocking

equations

and

graphical

methods

lch.

2

pipeline.

This

process

can be imagined as fitting a throttle

in

the

pipeline

of such

a

size that the

head drop across

it is equal

to the friction loss that it represents. For

instance it is

possible

to imagine

a throttle

-

sometimes called a choke

-

at the

upstream end

of the

pipeline,

another at the midpoint and a third at the valve each of

--.1-:^l- ^ l-^- :- L--l ----^l ^ ^l-:-.l ^f 1l-^ z^t-l t-l-t:^- t^^^l l^-^

wilrurr

uaus€s a ufoP

tll Iteau cquar tu ullc

rrlfq

ul

Lne ruLal rfrcuon rleau russ.

Schnyder

[4]

thought of concentrating all the loss at a throttle at the reservoir in1923

and

a few months later

Bergeron

[5]

suggested

the

same

idea independently.

Bergeron

placed

his

throttle at the

valve,

however.

The

technique,

when

only one

throttle

is

used

is called the

Schnyder-Bergeron

method.

Many other workers had

prefigured

this

idea

-

Moens

and Korteweg for example.

Angus suggested

the idea

of

inserting the midpipe throttle

in

conjunction

with

the

Schnyder-Bergeron

throttles.

2.5.1 The

Schnyder

method

Consider a frictional

pipe with a throttle

at

the

reservoir end

-

the

position

suggested by

Schnyder.

The

pipeline

friction

is replaced by the head drop across the

throttle

so the

head at,4

is correct

(although

nowhere

else)

for a frictional

pipeline.

The

frictional loss is

, fLq

nr:ffi:kqlql.

Deduct

the kqlql expression

from the horizontal reservoir characteristic

giving

the

frictional

characteristic for B'which

isthe relationship between the

head and

flow at

the

point

B'

just

downstream

of the throttle.

The steady

state

is at the

point

,46 and B'o.s; Bo.r is immediately above it

on

the

B

reservoir line.

The distance

BB'r.tis the head loss across the throttle and can be

seen

to

be equal to kqlql. An eagre

II from Bi,.rwill

give

A

1.s.

All

eagres

that reflect off

the

reservoir throttle

must

reflect off the

B'

characteristic not

off

the

B

characteristic

as

no

eagre can ever cross a

throttle. The technique is simple and is the one suggested

by

Schnyder

(Fig.

2.10). It

gives

tolerably accurate results

at

the

valve

but

elsewhere

the

accuracy

is reduced. At the

valve,

the entire

pipe

friction has occurred and the

method

assumes

that throughout

the

pipe

the

entire

pipe

friction

has

already

been

lost.

Only

at

the

valve

is this

completely true.

It

is

worth noting that friction

does attenuate

the

wave

and

the

pendulation

that

occurs

after the

valve

is completely

closed

effectively attenuates the

wave.

2.5.2

The Bergeron

method

As stated

earlier, Bergeron

used one throttle located at

the

valve

(Fig.

2.11).

In such

a

circumstance it adds

to the

losses created by the valve;

so the

throttle loss kqlql

must

be added to the ordinates

of

the

valve parabolae.

Note

that the eagres

reflect

off

the

downstream'throttle and

do

not

pass

through

it. The

head loss across the

throttle

is /ro,

-

lro and

this can

be seen

to equal kqlqlas

it

should. Also notice that in this case

the wave

is not attenuated

after

valve closure is completed. In

this connection

it may

be

found of interest that a

partial

closure will

produce

wave

attenuation;

it is only

Sec.

2.51

The introduction of

friction

to the analysis

Fig. 2.10

-

The Schnyder method.

Fig. 2.11

-

The Bergeron method.

complete

closure

that

does

not cause

any

attenuation

whatsoever. It is worth

realizing that

only more

sophisticated

methods are capable of

handling friction

accurately.

2.5.3 The Angus throttle

Angus

[6,7]

suggested

the use

of multiple

throttles

(Fig.Z.tZ).

He also suggested

throttles located

other than

at the ends of

a

pipe.

To

illustrate

this technique consider

a simple

pipeline with a

throttle

in

the Schnyder

position

and one

in the central

position.

From this

case it

will

be seen

that any number of throttles can be used and

63

64

The

Allievi

interlocking

equations

and

graphical

methods

lch.2

hr

=

tqz

hr

=t'z

k

q2

Fig.2.72-

The

Angus

throttle.

give

correspondingly

better

accuracy

but

the

complication

of

the

technique

increases

exponentially

with

the

number

of

throttles

and

itwill

be realized

that

tire

computer

.

methods

given

in later

chapters

are

far

superior.

One

only

needs

a

soft

rubber,

drawing

board,

paper

and

pencil

to perform

this

analysis.

A

computer

costs

much

more

than

such

items

ind

needs

a

reliable

electricity

supply

which

is not

available

in

every

country

in

the

world.

There

are

circumstances

in

which

the

graphical

method

will prove

uriful,

but

it requires

intense

concentration;

the

slightest

unnoticed

slip will

produce

errors

which

will propagate

throughout

the

analysis,

affecting

every

value

aJit

passes

up

and

down

ttre

pipeiinl

or

network

at

wave

speed.

There

are

two

systems

of waveriders_moving

up

and

down

the pipe.

When

they

meet

at

the

central

throttle,

because

the

flow

is

moving

from

the

upsirlam

end to

thL

downstream

end,

the

head

on

the

upstream

side

will

ullouyt

be larger

than

that

on the

downstream

side

(unless

the

flow

reverses);

so the

eagre

iine

trori

the

upstream

side

at

the

throttle

must

be

higher

than

the

one

coming

from

the

downstream

side.

At

the

throttle,

the

head difference

between

them

mJst

be

the

head

loss

across

it.

To

illustrate,

consider_the

eagre

coming

from,4r.6

and

the

eagre

coming

from

Br.s.

They

cross

and

the

class

II

eagre from.4r.o

must

lie

above

the

class

I

eagi

from

Arr.

1.nit

distance

mgst

be

picked

off

the

0.shtline

vertically

below

using

di-viders

1rig.

i.f:y.

Case

A

is

wrong

because

ft,

o

is

smaller

than

x^

and

case B

iJwrong

becauie

ft,

sis

larger

than

xr.

The

correct

answer

lies

between

these

two

and

must

be

found

by

irial

and

error.

The

technique

is

simple

and

quick.

"o.75

L

O

uO.25

Sec.2.7l

Junctions

Fig.

2.13.

2.6

JOINTS

At

a

joint

the

flow

is conserved

across

the

joint

and the

head

is the

same

on either side

of the

joint

if the velocities

on both

sides

are

so low

that the

kinetic

energies are

negligible

compared with

the pressure

heads.

The

only variable

that

changes at

a

joint

is

the

slopes of the

eagre lines.

Such a

problem

is

not difficult (A,

and

Ararethe

cross-sectional

areas

of the two pipes

and

c. and

crare

their

respective

wavespeeds).

2.7

JUNCTIONS

always

used

it for

this

purpose

since

first

reading

the

paper.

First

consider

the

simplest

sort of

junction

which

is a

three-way

junction

(Fig.

2.14).

For

ease

of comprehension

assume

that

wave

reflection

times

aie the

same in

65

hL:

hi:

ho!

66

The Allievi interlocking equations and

graphical

methods

lch.2

These two

equations

solve any

junction

provided

that the

local losses are negligible.

Draw

in two class II

eagres coming

from reservoirs B and

C starting at time

0

(Fig.

2.14).It

is assumed,

again

for

the

sake

of simplicity,

that

the

points

Bn

and Cn

are

known. At any given value

of ft the

value

of

qo*

qfcanbe

determined

by adding the

abscissae

of the two eagres

and a compounci

iine oi orclinate h

andabscissa

qo + q'"is

thus obtained.

This

can be done

by using dividers either

to

perform

the

addition

or

to

locate

the

points

on

the

two

eagres

where q

is zero and thus

to establish two

points

on

the

compound line.

Where

the compound line intersects

the eagre

from,4 is the

location

of

point

Di'j. The

points

D[',

and

D[,are

located

by drawing a horizontal

line

through

D'o'.', to intersect

the two

eagres

from

B

and C. To

show

how the

technique

can be used

to solve a very simple network,

the

first two steps of the

analysis

are

shown in Fig. 2.14. Friction has

been neglected;

reservoirs have been

Fig.2.l4

-J'5

cto

cz.o I

Xzi

Nole

1

lines

ore

porollei

Fig.2.15.

assumed

to have equal

surface

levels and eagre slopes in

pipes

1 and 2 have

been

assumed

to be

different.

Going

through

the

process

C, is obtained

from

Di.r.

Combine

eagres

from.4, and

B, to

give

the

$t.r

line. Where this intersects the class I

eagre

from C, defines D'r'.!. Draw

the horizontal through D'r'.; to intersect the class

II

co

cot

Cro

Sec.

2.81

Pumps

eagre

lines

from

B, and

Cr,

so

obtaining

Di.,

and

Di'r.

Br.n

and

Cr.s.

Then combine

the

two

eagres

from

Br.n

and C2.6

to

give

$2.5

and

where

this

intersects

the

class

I eagre

from

/r.s

gives D2'.'5.

The horizontal

through

D!'!

gives

D'r.5

and

D'2'.5.

Theprocess

can then

be

repeated

until an

adequate

time has

been

explored.

2.8

PUMPS

Although

valves are

very common

devices

to find

in

use on

pipelines

the

pump

may

well be

an

even

more

important

boundary

condition.

Pumps

are

used

to

pump

sewage

from

suction

collection

wells up

and out

of

the catchment

area

for

that suction

well into

another

catchment

area in

which there

is

a sewage

treatment

works-

In

raw

and

clean

water

distribution

networks,

pumps are

used

to

increase

pressure

and

so

flow;

such

pumps are termed

booster

pumps. Oil

and

petrochemicals

are

commonly

pumped unO

dirttibuted

through

pipelines. Slurries

are

now

handled

through

pipetines.

Nowadays,

almost

all

fluids,

Newtonian,

non-Newtonian

and

other

types,

are

pumped

through

piPelines.

f,r.pr

create

transient

conditions

wheneverthey

change

speed;

so,

when

a

pump

is started

or

when it

is switched

off

(tripped), transient

conditions

are

generated.

Usually

pump trip

creates

worse

transient

conditions

than

pump start-up.

This

is

primaiity

due

to

the

fact

that,

at start-up,

waves

travel

through

fluid

that

is

travelling

iaster

and

faster

as

flows

increase

as

the

pump

gets up to

normal

operating

speed.

The

waves are

travelling

through

fluids

in

which there

are

pressure

gradients

caused

by

friction

and as s.en

on

p. 39

these

cause

attenuation

of

the

pressure

transients'

At

pump trip,

the

opposite

effect

occurs

as

fluid slows

down;

the

transients

travel

itrrough

liuid

which contains

progressively

smaller

frictional

pressure

gradients,

and

so

the transients

are

not

rapidly

attenuated'

Consider

the case

of

a

rising

main

(Fig.

2.16).

Fig.2.16

-

The

rising

main.

2.8.1

Pump

start

up

If it

is assumed

that

the

full

motor

torque

is

applied

to

the

rotating

masses

of

the

motor

and

the

pump,

the

rotational

speed

will

rise

very

quickly

to

the

operating

67

68

The

Allievi

interlocking

equations

and

graphical

methods

lch.

2

speed.

Given the torque versus

speed

curve

(available

from

the

motor manufac-

turer),

it

is easy

to calculate

the

growth

of the

pump

speed and

to

perform

a

full

transient

analysis.

However,

in most

situations,

an

assumption

can be

made which

will

produce

an overestimate

of the

pressure

transient

that will

be

produced

at

start-

up.

and this

assumption

is

that the

pump

will

reach full

speed in zero

time. If the

start-

up

time

is effectively

less than the

pipe period

ZLlc the

instantaneous

start-up

transient

will

have the

same magnitude

as

the actual transient.

In

the full

scale

world,

this

assumption

is

usually

acceptable

and

only

in case of the

start-up

of large pumps

on

relatively

short

pipelines

will

it

be necessary

to

carry out the

detailed

analysis

mentioned

above

(Fig.

2.17).

Fig.

2.17

-

The

graphical

analysis

of

pump

start-up.

The

pump

characteristic provides

the

boundary

condition

at P.

Assuming that

the

pump

has

a reflux

(non-return)

valve,

then Po,

Rj.r,

and Ro.,

are

coincident.

A

waverider

starting

off

from the reservoir

at

time

0.5lwill

arrive,

along

a class I

eagre,

at

the

pump

at time

1,.0T. Reversing

this

waverider

and sending

him

back up

to the

reservoir

along a class [I

eagre

gives

the

Ri.r

point.

Repeat

this

sequence to

complete

the

analysis.

2.8.2

The

accelerating

-

decelerating

pump

Let

the

inertia

of the

rotating

parts

of the

pump

set

(including

that

of

the

electric

motor)

be

denoted by

I. In the

SI system of units

this value

must

be in units

of

kilogram

metres

squared and

in the

American

system

of units

(which

used

to be the

UK

system also)

it must

be in units of

slugs feet squared

units.

It

is

possible

to

get

a

curve

of torque (in

newton

metres)

against speed

(usually

in revolutions per

rninute)

from

any

motor

manufacturer.

t

h

s

I

Y

Sec.

2.81

Pumps

Let torque

be denoted by T.Let the

power

transferred

to

the pump

be denoted

by

P.

|

,et the

angular

velocity

be denoted

by O. Let the

angular

acceleration

be denoted

by A.

Let the rotational

speed be N in revolutions

per

minute.

Let the

rotational

speed

at

the

start of

a At interval

be Nt rev/min.

Let the

rotational

speed at the

end

of

a

Ar

intervai

be

fr'2 revimin. Let

Ar be the

time intervai

of

the

integration.

Let

the

pump

efficiency be denoted by E. The

torque applied

by the

motor

at any time

is

I-

and the

resisting

torque

generated

by the

pump

will

be

To- Then

T*- Tr: 792

and

P: T{2.

So

P:1QQ

but

69

p:

IZnNt

2r Nz- N,

60 60 Lt

and

so

Nz:Nr,]ffi

Now P

:

Tf)

from above and T

:

T^

-

wQHl

E; so

P:T^{2-ry

but l-fl which

equals

the motor

power

P-

and

wQHIE

is the

power

absorbed

by

the

70

pump;

so

The

Allievi interlocking

equations

and

graphical

methods

lch.

2

N,=N, *#f,(r.,-ry\

This expression

*o.Ur;:rr,",

,,.n*O

""0

",

pump trip. For

pump

start-up,

it is

essential

to have either the

I-

versus

N

curve

or

the P,,.

versus

N curve from the

manufacturer but this is not always

easy to

get.

At

pump

start-up

the

value

of

N, initially is zero.

Using

the

motor

power

curve to

get

the

value

of

P*, N, can easily

be calculated from the above equations.

A

new

value

for

P- can

then be obtained

and

theprocess

repeated until the time duration of

the analysis

has been covered.

At pump trip,

P-

goes

to zero instantaneously;

so the

value

P- disappears

from

the

equation

for

N2.

Note

that, in this circumstance, the

pump

speed

will

conti-

nuously decrease. See

pp.

104-L07 for further

comment

on this topic.

Consider

the case of

pump

trip

(Fig.

2.18).

Vo

is the steady state

pump

R' characteristic

?t

N=Ns

reservorr

N=N.,

characteristic

Fig. 2.18

-

Pump trip.

characteristic.

ry,

is the

pump

characteristic

for

the speed N, obtained

from the

equation

above

for a Arvalue of

T(

--ZLlc).

Similarly

the

ry2,

{3,

€tc.,

curves are for

the

corresponding

multiple of

Z using

corresponding

Nt, N2,

N3, etc.,

values using

Stepanov's

pump

head equation

to

give

the curves

H

:

ANz

+

BNQ

-

CQ'.

steady

state

pump

characteristic

Sec.

2.81

Pumps

This last equation

is developed

in this book; see

pp.

101-102. The constants,4,

B

and C can

be obtained

from

the

pump

manufacturer's characteristic

curve

by simple

substitution

of three

pairs

of.

H,

Q

values

into

the

equation

and then solving

the

three

resulting

equations

for the

required constants.

Alternatively,

the dimensionless

products gHlNzD2,

8lND3

can be

used

to

calculate

values so

as to

be able

to

plot

the

Vr, Vz, {3,

etc.,

curves. This may

be

necessary

when the

pump

is

not of

the type that will fit the

Stepanov

equation

(e.9.

axial

flow

pumps). Many analysts

use a constant

value for E

throughout the run

down.

If the efficiency

curve of

E

versus

Q

is available and if

the characteristic curve

(Fig.

2.19)

is available,

it is

possible

to establish the relationship

between the

Fig.2.19

-

Pump characteristic

curves.

efficiency,

the

flow

and the speed

(see

p.

104).

From these,

values

of E can be

obtained

which can

be

used in

the earlier equation

for

N.

Acomment

which

applies

to all

graphical

methods is

that the

periods

of

the

pipes

which make up the

system

must

be in

relatively simple

ratios one

to another. If they

are

not,

the

graphical

analyst

is faced

with

an almost

impossible

task. The reason is

that a

value of Ar must

be chosen

which will be the basis of the

entire analysis.

If this

value is too small

a

fraction of

the

T values that apply to

the

various

pipes

in the

network,

the

graphical

analysis

will

become of

such

great

complexity

that no analyst

could

take it on.

It is also

necessary

for all

the

various

Z

values

of

the

pipes

in the

network to

be in simple

ratios

to

one another:

3:2 or 1:1 or

1.:2, etc.If

they are not, it

is

necessary

to modify

the

network in

such a

way that the ratios

are simple

and the At

value on which the

analysis

is based

is

adequately large.

It is usual

to

pick

the smallest

I in the

network

for this

value. The resulting

network

rnay not

resemble the real

network

to any

great

extent,

in

which

case

the results derived

from

it

will

have little

7l

{

72

The

Allievi interlocking

equations

and

graphical

methods

lch.

2

relevance

to

the real network

also

and the

analysis

will

not

be

worth

doing.

Nowadays

this would

mean that a

computer program

would

have

to be developed,

employing techniques

described

later

in

this

book.

In the

past,

before

the advent

of

computers,

the

poor

modelling would

have

had to be accepted.

Very

high standards

of modelling

can now

be

achieved in

optimal circumstances

and

using computer-

based methods,

but the graphical

techniques

described

in this

chapter

are

worthy

of

study

for

their

ingenuity

and

the insight

that their comprehension

provides.

The method

of characteristics

3.1 INTRODUCTION

The methods discussed and

demonstrated in

can be

generalized

to

the

solution of

small

networks

and this

was

done

in the

period

between

the

1920s and

the 1950s. The techniques

are

very

well described

in

books by

G. Rich

and

C. Jaeger.

The difficulty with such methods

is that they

are founded

upon theoretical

bases

which

are not

completely accurate

(see p.

45).

The

errors are

caused by

ignoring

the

convective terms v(1hlOx) and u(0u/0x) and

the

friction term

Zfr\fild

in the basic

waterhammer

equations

(1.1)

and

(1.2).

These

would not be

important

if the wave

speed were to be large in comparison

with the

stream velocity,

throughout

the

period

of the wave. During the

passage

up

and

down

a

pipe,

a wave

can cause

sections

of the

pipe

to

be at

low

pressure,

whilst

in other

sections the

pressures

can

be large.

Such

low

pressures

can cause significant reductions

in the wave

speed and these,

in turn,

can

cause the insignificant convective terms

to become

significant and,

as these

are

not modelled, introduce errors.

Additionally,

using

these methods,

the

labour

in

analysing a really complex network should

not be

underestimated.

It

is

extremely

tedious to

perform

one such analysis but,

to make

a

complete assessment

of the

safety of a

network it is necessary

to

perform

a large

number

of them;

this would

be

so

difficult to organize and

perform

as to be unacceptable.

A

graphical

analysis may

well be unacceptable

in

view

of the

comments

made

in

the last few

paragraphs

of Chapter Z.The layout

of

the

scheme will

probably

have

to

be amended,

short

pipes

being incorporated

into longer

pipes

and

almost all

the

pipes

having

to

have

their lengths

altered, at

least

a

little,

so that their peiodsZLlc

are simple fractions

or

integer

multiples

of

a

chosen

pipe's period.

Such an

amended

layout

may well

have small similarity to the

prototype

network.

For the

above reasons

a

more accurate technique

of

analysis had to be

developed.-

Fairly

obviously, the differential equations

of waterhammer

could

be

integrated

directly

by finite difference

methods by using

Ar

and

At values chosen

at random.

Then

by

various

simple methods, using expressions

for Aft

and Au,

formulated

in

74

The

method

of

characteristics

lch.

3

terms

of /r and u

values

already calculated,

expressions for h and u

at any

given

x and

I

value

can be

obtained which

can be

solved

for ft and u at

everyx and rincrement.

Such

a technique

would

completely ignore

the

presence

of

wave

mechanisms

and would

certainly

produce

results

of

doubtful

accuracy.

A sophisticated

and accurate

version

of

sueh

a method is

the I-ax--Wendroff

[9]

method. It

suffers

frorn linnitations

concerning

the analysis

of boundary

conditions but

permits

the use

of relatively

large

At values.

A

few

years

ago, the

cost

of computing

was

a big

factor in

the choice of the

method

to be used and

large

Arvalues

permitted

reductions

in

the cost

of analyses; so

such a

method

was

attractive.

Now

,3}-bitcomputers

with very

large random-access

memories,

operating

at

very

high

speeds

are available

at

very

low

prices;

so the cost

of

computing

has

greatly

diminished as a

factor

in the

choice

of method.

3.2

THE

MBTHOD

OF CHARACTERISTICS

The

method

of characteristics is

a technique

which

is free

of all these

defects and is,

up to

the moment

of writing, the most accurate

method

of

analysis available. It is,

currently,

the method

of

choice

of

most

analysts.

The

waterhammer

equations are:

(1.1)

(1.2)

This

result has

considerable

similarity

to

the chain

rule for

total differentiation.

To

clarify

this

point,

write the

definition

of a

total differential

of a

variable

$

which is

dependent

upon

two

variables x

and

r:

c,

40.

,40"-

d0:

Ar

hx+

Ui

or

.

this

result

by 6t:

(4*u*'tu\'l'\-o

\c

d

/

d0 a0

d.r

,

A0

-:

dt 0x

dt

Ot

-$(*)

*#*#:o

and

#:'-'

Sec.

3.21

The

method of

characteristics

75

(3.3)

(,,

*')

*.3)

*

.

(,,

*,)

*.3)

(,'*4

*.3)

u+2$:o

So

(3.4)

(3.s)

dh

.

u

0u, 1du

,Zfulul

^+-^

*-;*

-0.

ox

gdx gdt gd

Multiply

equation

(1.2)

by the wave

speed c.

Oh cu

0u

.

c 0u

.

Zcful|

^

C-r--T-=-i--

:v

.

dx

8ox 8ot

ga

Add

equation

(L.L)

to equation

(3.1):

!*!*c(u+c) 3*9 !*4

c:o

(u+c)-rr

ot

g

ox

gat

gd

Collecting

terms,

Ah Ah c2

0o

u

|

+=+-

=:0 ,

ox dt

8ox

(,,*')

*.u")

o*;(,,*')

*.*)

(3.1)

(3.2)

friction

is correctly

described.)

These

results

mean

that,

if

a

line is

drawn

in an.r-t

space

at

a slope

of

drldr of

t/(u

+ c) then

along

this

line

the

value

of

6$

(which

is 6(gftlc)

* u * zfulvltld)

will be

zero.In

other

words,

ghlc

*

u + Zfulultld

will be constant

along such

a line.

The term

is sometimes

called

the

Riemann

invariant.

A line

for

which this

is true

is called

a

characteristic.

If,

instead

of

adding

equation

(1.1)

to

equation

(3.1), it had

been subtracted,

slightly

different

results

would have

been obtained.

These are

u+ry:o

If c may

be assumed

to

be

constant

in the

t-r space

being explored

(i.e. over

the Ax

and

Ar intervals

involved)

this

equation

can

be rewritten:

through

by

glc:

Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

Подождите немного. Документ загружается.