Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

36

The

differential

equations

of waterhammer

ICh.

1

C

wave

closed valve

Fig. 1.6

-

The situation

at time Llc.

The

length

DL

in Fig. 1.6

is therefore

(AplK)(nl\d2L

+

(A'p

d3lTE)rLlZ

(nl4)

dz

and

this

equals

L Lp(llK

+

dl(7|Q. So

6z:

t*(!..h)

The

additional

volume

of

length 6L

is

supplied

from

the reservoir

at the

velocity

u.

Note

that

it cannot

be different

from

this

value

because,

until the

wave

arrives

to

change it, it must continue

at

the

value u.

So

6L:uAt:

and

Lp

(rtK

+

dtTE)

+:rr(i

.+)

but

-

wu

AD:

w

Lh:--=-

'

gLLt

\P:eh:

Pcu

the

Allievi

equation

but

Simple

elastic

theory

l)

=

pvu(LlK+ dlTE)

'

JI

Sec.

1.41

Lp

(rtK

+ dtTE)

,l

Pc-:

uK+dlrE

'

This refers

back

to

p. 22and

explains

the substitution

that

was made

there

.

Therefore

1

,:@

but

Ap

-

pcD

(from before)

and so

Ir - \

Lp:'\/(# -)

,

v

\P(l/rK

+ dlTEl

Therefore

^'-

\/(gtw)(LlK+

dlrE)

'

Generalizing,

the

Allievi

expression

is

Lp=

pcLu

but in

this special

case

Au

:

u so

that

we have

Lp

pcu.

Of

course,

in

the

case

of

an

instantaneous

complete

closure,

Au

does

equal

v.

The

wave

rp""d

calculated

above

assumes

that

there

is no

longitudinal

change

in

the

pipe length

caused

by

Poisson's

ratio

effects;so

the

result

glven above

applies

to

the

case

of

a

pipe restrained

by

anchor

blocks

at

its end

and

at

every

azimuth

change.

Other

expreisions

are

available

for

different

cases

and

a few

of

these

are

presented

later

on

pp.

4243.

The

wive

form

for an

instantaneous

closure

is of

interest.

At

the

valve the

form

is

that

of

a square

wave

and

this

can

be

deduced

by

consideration

of

Figs.

1-5(al1-5(d)

'

The

period of

the

wave

is

4llc

but

unfortunately

the

practice has

developed

of

calling

the

time

that

it

takes

for

a

wave to

pass

up

the

pipe

and

return:

2Llc,the

pipe

period.

At a

point I upstream

from

the

valve

the

wave

has

the shape

glven in Fig.

1

.7 .

This

shape

can

againbe

deduced

by consideration

of

Figs.

1.5(aF1.5(d).

38

The

differential equations

of

waterhammer

lch.

1

volve closure

occurs

L

l,L

L,

c

\

{.

C

c

Fig.

1.7

-

The

pressure

head diagram

/

upstream

from the

valve.

At

the reservoir

where

I

:

L the diagram

degenerates to

that illustrated

in Fig.

1.8.

Fig.

1.8

-

Pressure head against

time at the

reservoir.

1.5.1

The

effect

of

friction

In

the foregoing

presentation,

friction has been neglected;

so the

head

everywhere

has

been assumed

equal

to

the

reservoir head I/. With friction

present

the steady

state

situation is as

illustrated

in

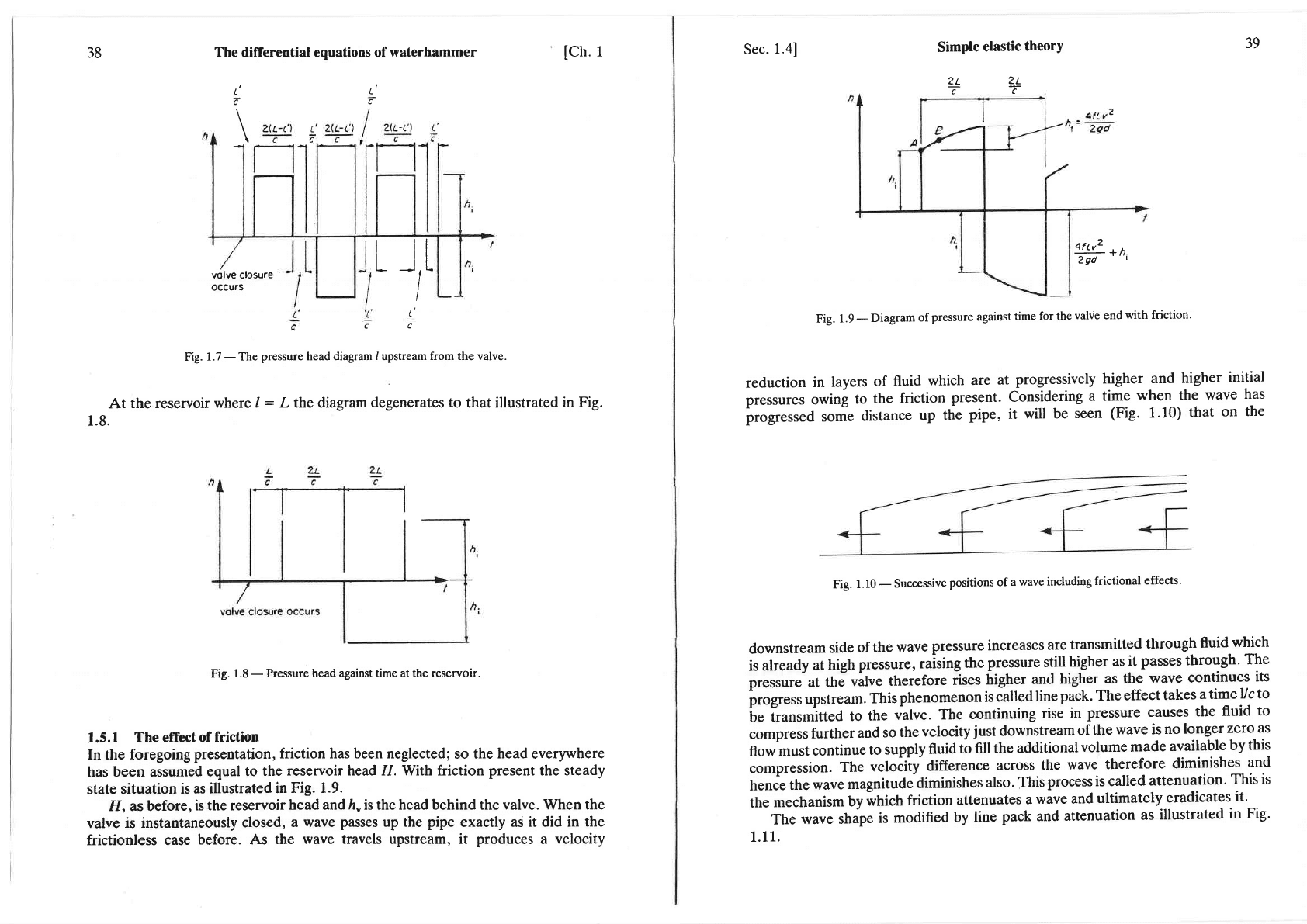
Fig. 1.9.

H, 6 before,

is the reservoir

head and

/r"

is the head behind the

valve. When the

valve

is instantaneously

closed,

a wave

passes

up the

pipe

exactly as

it did in

the

frictionless case

before. As

the

wave travels upstream, it

produces

a

velocity

Sec.

1.41

Simple

elastic

theory

4f

Lv?

* 1r.

?cd

I

Fig.

1.9

-

Diagram

of

pressure against

time

for

the

valve end

with friction.

reduction

in

layers

of

fluid

which

are

at

progressively

higher

and

higher

initial

pressures owing

to

the

friction

present. Considering

a time

when the

wave

has

progr"rr"d

sorne

distance

up

the

pipe, it

will

be

seen

(Fig.

1.10)

that

on

the

Fig.

I

. 10

-

Successive

positions

of

a

wave including

frictional

effects.

downstream

side

of

the

wave

pressure

increases

are

transmitted

through

fluid

which

is

already

at high

pressure,

raising

the

pressure still

higher

as it

passes through.

The

pressure

at the

nrlu"

therefore

rises

higher

and

higher

as

the

wave

continues

its

progress

upstream.

This

phenomenon

is

called

line

pack. The

effect

takes

a time

Vc to

-b"

trunr*itted

to

the

valve.

The

continuing

rise

in

pressure

causes

the

fluid

to

compress

further

and

so

the

velocity

just

downstream,of

the

wave is

no

longer

zero

as

flow

must

continue

to

supply

fluid

to fill

the

additionalvolume

made

available

by

this

compression.

The

vetoiiiy

difference

across

the

wave

therefore

diminishes

and

hence

the

wave

magnitudediminishes

also.

This

process

is called

attenuation.

This

is

the

mechanism

by

*ttirtr

friction

attenuates

a

wave and

ultimately

eradicates

it.

The

wave

shipe

is

modified

by

line

pack and

attenuation

as

illustrated

in

Fig.

1.11.

39

2L

?L

cc

40 The differential

equations

of waterhammer

'[ch.

1

Fig. 1.11-Line

pack

and

attenuation.

1.6.1 Separation

When

the initial absolute

pressure

is less than the wave

magnitude, a

phenomenon

known as

separation occurs.

When a.valve closes, a

positive pressure

wave

passes

up

the

pipe

which reflects normally

at the reservoir

end.

The

reflected

wave

runs

back

down the pipe

at

wave

speed,

reducing the head

to

the

original

value

and creating

a

reverse

velocity throughout the

pipe's

length. When

the fluid attempts to

move

upstream

at the

valve

end, it

is

restrained from doing so by the

presence

of the closed

valve;

the fluid is brought

to rest and

consequently

its

pressure

falls.

Under

the

special conditions

present,

this

drop

in

pressure

takes the local

pressure

below

atmospheric

pressure

on

down to the

vapour

pressure

of the fluid. At this moment

the

liquid boils at the ambient

temperature. The region

of

boiling

liquid extends

for a

distance

upstream

in the form of a

vapour-filled

bubble.

Swaffield

[1]

took high speed

cine

pictures

of this event

occurring in a Perspex tube and was able to demonstrate

that

the

vapour-filled bubble

was

of a

paraboloidal

shape.

The

phenomenon

can also

occur at crests in

pipelines where

the

elevation causes low

pressure

regions. In

some

circumstances the closure

of such a bubble can

cause a

high

transient

pressure

but in

others it

does

not occur.

Analytic techniques

of the type such as the method of

characteristics

(see

Chapter

3) are able to

predict

such high transients. When such a

bubble

opens and

then closes

again, the

event must happen

by

the movement of

liquid which

occurs at

velocities of

the

same order of magnitude as the main

pipeline

velocity.

Consequently

the

presence

of such

a bubble

causes significant

increases

in

the wave

reflection time

and such a

lengthening

of the

pipe

period

(zLlc)

is diagnostic

of the

presence

of separation.

1.6.2

Gas

release

Accompanying

the

generation

of

vapour there is also a release

of

gas

from

solution

in

the

liquid. This

process

commences

during

the pressure

reduction phase

and starts

head

at

valve

friction head

recovery

tlme

Sec.

1.41

Simple

elastic

theory

when the

pressure

falls

below

atmospheric

pressure. Very little

gas

comes

out

of

solution

at

pressures

just

below

atmospheric

pressure but

progressively

more

and

more

comes out

as

the

pressure

drops

further

and further.

The

presence of such

gas

bubbles

is not thought

to

have

much effect

upon the

formation

of

the

separation

bubble but

it is considered

by many workers

to have

a cushioning

effect

upon

its

closure.

This

is due

to the

fact

that the solution

of

gas

bubbles

is a slower

process than

their evolution;

so

gas

bubbles

are left floating

in

the liquid

after

the main

vapour-

filled

bubble

has collapsed.

They may

stay

in

existence

even

after

the

pressure has

risen significantly

and

for

quite

long

times. They

are

thus

available

to

reduce

the

magnitude

of

the

pressure

waves that

would otherwise

be

generated, by

decreasing

theiffective

bulk

modulus

of

the

liquid. See

p.

139 for

a more

complete

discussion

of

the

phenomenon

of

gas release.

fig. t.tZ shows

how

the typical

pressure

signature

of

a

pressure transient

in

a

I

l

I

/

t.f',

;;;.t;:;::."'"

diagram

for a

piperine in which separation

is occurring.

simple

pipeline is modified

by the

presence of separation.

Compare

this

diagram

with

fig. f

.i: which

is the

pressure

signature

of

a simple

pipeline

which

is not

experienc-

ing separation.

Fig. 1.13

-

Pressure

diagram

for

a

pipeline in

which separation

ir rro,

o""orring.

1.6.3

Some

observations

about

the

Allievi expression

In a

the

Allievi

equation

was derived

by a somewhat

devious

route

but fhis

route

did not

make

the

assumption

that

the

value

c was

the

wavespeed.

4l

ropour

heod

/nl

t

I

ft

II

t

l-_

--'

t

42

The

differential

equations of

waterhammer

'[ch.

1

The differential form

of equation

(1.6)

given

earlier, neglecting friction, is

Ah

ldu

:-*- .

-0

dx

gdt

andp

:

wh.

Lt: Lxlc

is the

time

required

to cause the change in

the

velocity

of

the

liquid

in the length Ax

and is

the time it takes the wave

to

traverse

the length Ax.

Therefore

Lp:

-Y

u*:

pcAD

g

Lxlc

Remembering

that Au is negative as the

wave

is created

by a downstream reduction

of

velocity

then so the

corresponding

head Aft

:

L,ptlw

-

c Lvlg. This is sometimes

called

the Joukowski equation. In eastern Europe it is ascribed to

Joukowsky

but in

the

West it is more commonly attributed to Allievi. The

author has also seen

it

attributed

to Moens and Korteweg.

1.7.1

Wave

speed

The

acoustic

wave

speed is

given

by c

:

l/

;Ktp).

If

the distensibility

effects

that

occur

in a

pipe

restrained

from movement

longitudinally

are taken into account the

value

of the bulk modulus needs amend-

ment to

take this distensibility

effect

into account, i.e. l/Kbecomes

1/K

* dlTE, and

SO

Ir

e-rtT-

V

(wts)(uK+

dtrE)

'

If

the

pipe

is

permitted

to expand

longitudinally and Poisson's

ratio effects are taken

into

account, the

pipe

being assumed to be restrained at

one end

but free to move at

the

other,

the bulk modulus can be modified as follows

replace llKby

UK+

G/T{)

614

-

1/m)

where

llm

is Poisson's ratio. Then

It

f

:

1I

\

(wtdll,tK+ (dtrE)(st4+Itm)l

'

For

a

pipe

in a rock tunnel

with concrete infilling between

the

pipe

and the tunnel

wall

(wtg)UtK+

@trQ(l

-

l.)l

Sec.

1.41

where

Simple

elastic

theory

d2t4ET

l.-

dzl4ET

+

(d7

-

dz)l4d.E.+

(m +

l)dlzmEp)

d is

the external

diameter

of

the

steel

liner,

d.

is the

external

diameter

of

the

concrete

infilling,

E isYoung's

modulus

for

steel,

.8"

is Young's

modulus

for concrete,

E*

youngl

modulus

for

the

rock,

llm

is Poisson's

ratio

for the

rock,

and

T

is the

wall

thickness

of

the steel

liner.

For a

plain tunnel

in rock,

It-

r \

/18-

'

I

':

V

\;uK

+aE")

For

a thick-walled

piPe,

,\

--

l(s

1

\

\w

l/rK+

(1/88)

(d4r- di)/

where

d,

is

the external

diameter

of the

pipe, d,

is theinternal

diameter

of

the

pipe,

E

:

Z.tOg

tS

x

1011

N/m

for

steel,

K:2.03067

x

I}e

N/m

for

water,

w

:

9810N/m

and

g

:

9.810m/s.

These

results

are fairly

straightforward

exercises

in

the

appli-

cation

of

Lam6's

theorem

and

the

application

of

the theory

of

elasticity.

1.7.1

Sudden

valve

closure

A sudden

valve

closure

is one

in

which

the

valve closure

is

slower

than

an

instantaneous

one

and

yet

occurs

in a time

less

than

ZLlc,the

so-called

pipe

period.

A

valve closure

can

be

approximated

by

a series

of

very small

steps

of closure

spread

over

the

period of

time

duringwhich

the closure

occurs.

Each step

causes

a Au

d-ecrement

and

i

corresponding

wave

which

travels

up the

pipe

and

back

again.

It

will

be

realized

that,

if

the

iast

wave

created

during

the

closure

could

be emitted

before

the

first

wave reflects

back

negatively

from

the upstream

end,

the

sum

of

all

the

initial

positive small

waves

will

be

the same

as

that that

would

have

been

produced

if

the

valve had

been

closed

instantaneously.

Conversely,

if any

wave can

be

reflected

back

negatively

from

the

upstream

end

before

the last

wave of

the closure

is

emitted,

the

,"r.tlting

*ave

must

b-e

smaller

than

a

wave

produced

by a closure

in less

than

a time

of ZLlc.

Thus

the

magnitude

of

the

wave

generated by

a sudden

closure

of

a

valve

at the

end

of

a simple

pipeline is

equal

to

that

of the

wave

produced by

an

instantaneous

closure

but,

if

theilosure

is

not sudden,

i.e.

the closure

takes

longer

thanZllc,

the

magnitude

of the

wave

produced

is smaller

than

that of

an

instantaneous

closure.

There

are

many

circumstances

in

which

a

pipeline

could

burst

under

the

pressure

exerted

by a sudden

closure

or

even

under

the

pressure exerted

by a

somewhat

slower

cloiure.

For

very

long

pipelines,

the

value of

the

pipe

period can

be

very large

'

43

44

The

differential

equations

of

waterhammer

lch.

1

In this

situation

what

may

seem to

be a

very

slow rate

of

valve

movementcould

result

in a

sudden

closure with

the

consequent

generation

of transients

of large

magnitude.

In the

case

of a

network,

it can

be difficult

to

establish

a

value

for the

reflection

time,

i.e.

the pipe

period.

A

method

of analysing

slow closures

and complex pipe

arrangements

is needed

as the

techniques

so far described

are

not

suitable

for

such

cases.

The

introduce

some

of the earlier

techniques

that

were

developed

in

the

period

between

approximately

1910

and 1960.

No

adequate

computing

technique

was

available

during

this period;

so the methods

developed

were

of

a

graphical

type

and usually

of a

high

order

of ingenuity.

Quite

complex

situations were

analysed

but the

techniques

were

tedious

to perform

and required

a

very

high

level

of concentration

to carry

out. Nowadays

techniques

using

computing

are used

which

give

higher

orders of accuracy

and require

far less

effort

to employ.

For details

of

such methods

see Chapter

3 et

seq.

The

Allievi

interlocking

equations

and

graphical

methods

2.I

ANALYTIC

METHODS

Any method

of solving

a slowly

varying

hydraulic

control

rnust be

based

on

a solution

of

the

waterhammer

equations.

Unfortunately,

these

equations

belong

to

the class of

hyperbolic

partial differential

equations

which are

insoluble

analytically.

However,

if Certain

ofthe

terms

in

the

equations

are small

enough

to

be neglected,

they reduce

to analytically

soluble

forms.

Rewriting

the

partial

differential

equations

of

water-

hammer

developed

before:

-

Ah

c2

Ou

0z

:TLt-

T-

a--.q-:.r,

dt

dx

gdx dx

Oh.uOu,LOu,2/ulul-

Irl

--t1--J-r-r-

r-n_

a'-;

ar-;

u-

gd

-

Usually

u

is first

order

and

c is

third order

but

in some

circumstances

c can

fall to much

lower

values and then

it

will not

be

possible to regard

0ul0x

and)h/Ox

as

negligible.

If

friction

is a small

fraction

of

h, as

it can

be

when

either

there

is

a nearly

closed

valve

at

the end

of a

pipeline or

there

is a

nozzle

there, it

can

be

permissible

to

neglect

friction.

When these

three

terms

are

small,

the

two equations

of

waterhammer

reduce

to

46

The Allievi interlocking equations

and

graphical

methods

lch.

2

Fig.2.1-

A

wave

entering a

pipe.

Rearranging,

0u

-sAh

-:--:

-

t^,

dx c' dx

Differentiating

the

first of these equations

with

respect to

respect

to.r,

ah

_:

0x

0u Ah

-_- -o-

0r

o0x

t ) ^

dn

-c'du

-:

0tg0x

-10u

g0t

Ox Ot

c2

azh c202h

aP:-a;,

Azh

,

02u Azh

aP'ano**:-ga*,

(2.r)

(2.2)

(2.3)

(2.4)

r

and the

second

with

(2.s)

02u

(2.6)

Analytic

methods

47

Sec.2.1l

2.2.1

The

wave

equation

Equation

(2.6)

is

recognizable

as

the

wave equation.

Von

Riemann's

[2]

solution

of

it

is

well

known

and

given in

all

textbooks

on

differential

equations.

It

is quite

simple

to

integrate.

The solution

is

and

Dimensional

considerations

show

that

the

F(t

+ xlc)

and

f(t

-

xlc)

terms

are

contributions

to the

total

head

and

will be

shown

below

that

they

are

both

waves'

one

travelling

upstream

and

one

travelling

downstreat.--

-

An

observer

travelling

upstream

ai a

velocity

c

will have

an

equation

of

motion

of

x:

L-

ct assuming

that

le started

at

time

/

:

0

at the

downstream

end

of

the

pipe

where

x:

L. Subst'ituting

this

value

of x

into

the

F(r

+ xtc)

term

gives F(Llc).

So

for

this

observer

the

F(t

+ xlc)

term

will

remain

constant

as

he

travels

upstream.

Similarly,

in

the

case

of

an observer

travelling

downstream

at

a

velocity

c,

whose

equation

will

be

l:0*c/

(assuming

that

he started

at

x=0

and

r:0)

the

term

f(i

-

xlc)will

becom

e

f(t

-r),

i.e.

/(0I

so

for

this

observer

too

thef(x

-

cr)

term

will

b"

*nri*t.

If

these

terms

are

constants

for

appropriate

observers,

it

follows

that

they

must

be

waves

travelling

at the

same

speed

and

in

the

same

directions

as

the

appropriate

observers.

2.2.2

Wave

reflections

If one

considers

awave

startingfrom

the

downstream

end

andfollows

its

progress

up

a

pipe, as stated

above,

it

propagates

up

the

pipe with

constant

magnitude'

When

it

reaches

the

reservoir

at

the

upstreu*

"nd,

the

time

is

Llc

and

the

x

value

is 0

so

the

F

term

is

F(Llc+

0)

which

is

F(L/c)

as

obtained

before.

However,

the head

must

behs

because

the

reservoir

imposes

this

value upon

the

fluid

at

the

entrance

of

the

pipe.

Substituting

this

value

into

the

head

equation

gives

h:

ho+

r(r.)

.('-:)

u:uo-:["('.o)

-('-r]

ho:

ho+

r(r.:)

-('-:)

and

so

F(r+

xlc)

:

-

f(t-xtc)for

this

case.

At

this

moment

f

=

Llc

andx

:0

and

so

F(t

+ xtci

:

F(Ltc)

.n,i

1r

-

xlc):

f(Llc).

A1

F(r

+ xlc)

:

F(Llc)

it

follows

that

4ftr1:

-f(Ltc)'.Letthe

time

pipe

periodZLlc

be

designated

T'

To*

consider

a

wave emitted

from

the

downstrea.

"ttd,

at a

time

nT;it

travels

up

the

pipe, takin-g

Llc

(i.e.0.5D to

get

up

to the

reservoir

and

travelling

with unchanged

magnitude.

It

48

The Allievi

interlocking equations

and

graphical

methods

[Ctr.

Z

is

then negatively

reflected and travels back

to

the downstream end as an

/

wave

taking

an additionaltime Llc

(i.e.

another 0.5D

but

with

opposite sign

to that

that it

had

when

it first set

off. Denoting

the Fwave

(the wave that travels in

the

upstream

direction)

at

the

downstream end of the

pipe at

time nT by Fnr and denoting

the

/

wave

that is reflected

back to the downstream

end of

the

pipe

at time n ? * Iby

f

nr

+

t

thenf".*

1

:

-

f

..

Using

the

velocity

equation

and

considering what must happen

at the downstream end

when

it is

closed,

i.e. the

initial

velocity

must

be

zero, it

will be

seen

that ue must

equal

zero as must

u also.

So

at

a closed end,

F(t + xlc):

f(t

-

xlc).

From

the foregoing,

two important statements

can be made.

(1) At

the open end

of a

pipe, wave

reflection occurs

with

equal

magnitude

but

opposite sign.

(2)

At a closed

end,

wave reflection occurs

with equal

magnitude and the same

sign.

In

other

words at an open end

there is a

total negative

reflection and at a closed

end

there

is a total

positive reflection.

In the case of a simple

pipeline, it is also

possible to

say

that a

wave

starting

off up

the

pipeline

will

encounter

waves

coming

from the

reservoir which were initiated

from

the valve

end

one

pipe period

(ZLlc)

earlier. These waves

will have equal

magnitude

and

opposite

sign

to the earlier

initiatory

waves

because of

the

negative

reflection

that

they have experienced

at the

reservoir.

2.3.1

The Allievi

[3]

interlocking equations

Extending the notation

that has

already been introduced

in the

preceding

section,

let

f

denote a wave starting

from the

downstream end

of the

pipe

at a time of

n

x (ZLl

c)

and

f,

denote a

wave arriving at

the downstream

end of the

pipe

at

a time of

n

x (ZL/c),

i.e. the

location

is at L and the time

tis n(ZLlc).

Writing

the equations

for

successive

times 0,7,2T,3T,

..., flT,

0o: uo

-tfr"-

fo\,

ur: uo

-l<rr-fr),

uz: uo

-Ifor-

fr),

ho: ho+

Fo

+"fo,

ht: ho+

4+

h,

hz: ho+

F2+

f2,

hn: ho+

Fn +

f

,,

-

f,),

where

n is the number

of

pipe

periods

(zLlc)

in

which

the change in

the downstream

hydraulic

control setting

occurs.

The upstream hydraulic

control

must next be specified if

a solution

is to

be

obtained. Consider

the simplest

case

to

demonstrate the technique, i.e.

an upstream

reservoir. It will be remembered

from before

that at a

reservoir a

complete

negative

reflection

occurs

described

by the

relationshiP

f

,:

-

Fi-, where i is

an integer

of

Drr:

Do

-It'"

Sec.

2.11

Analytic

methods

49

value

lying between

0

and

n.

Substituting

for

all the/values

and bearing

in

mind

that

/o

must be

zero

because,

before

time

zero,

flow

was steady:,

head equations

and subtract

the

velocity equations:

ho: ho+

Fo

+

0,

hr:ho+F

-Fo'

hz: ho+

F2-

Fr,

hn: ho+

Fn-

Fn,

hL+

hz:

Fr*2h6,

h2+

hL--

F2-

Fo+Zho'

uo:uo-f{r'o-o),

ul

:

Do

-ltrr+.fo),

Dz:

Do-l<rt+

fr),

D,,:

uo

-l<n"-

f,-r).

ur-Do:

-3ar,

Dz-

Dr:

-

f{n,

-

F,),

hn+ hn-r-

Fn-

Fn-z+zho

From

the

velocity

equations

it can

be

seen

that

F,- F,-r=3r,-r

-

Di.

So

Dn-

Dn-r:

-1@^-

F,-r).

h,+

h,-r-Zho=

!(r,-r

-

ui).

I

These equations

are the

classical

interlocking

equations.

Up

to this

point no

assumption

has been

made

concerning

the downstream

boundary

condition.

In fact,

any

downstream

condition

can

be

handled

by

these equations,

provided that

they

can

be

described

mathematically

and

provided that

the

assumptions

on

which

these

equations

are based

apply. Of

course

the

pipeline

must

be simple,

i.e.

it

must

have

a

50 The Allievi interlocking

equations and

graphical

methods

[Ch.

2

reservoir at the upstream

end and all the

parameters

of the

pipeline

must be constant

throughout its length. To illustrate

how the

interlocking

equations

can

be used, the

downstream boundary

condition will be assumed to be a

valve.

This is the case that

Allievi

used to demonstrate the technique but it is emphasized that

the method

is not

confined to downstream valves.

Also it should

be

realized that it can be adapted to

deal with more complex

circumstance

than

the simple

pipeline.

It

seems

improbable

that

any modern analyst would want to employ these more

complex approaches,

even though

they are

possible.

Modern approaches are far more

capable

than is the

Allievi

rnethod,

but

the Allievi approach is ingenious and

enables

the

student

to

understand

the fundamentals of

pressure

transients. For a detailed

exposition

of

these

techniques

see G. Rich's

Hydraulictransients and

C. Jaeger's Engineeringfluid

mechanics.

To illustrate how the above equations

can be

used, the case

of a slowly

moving

(opening

or closing) downstream valve

will

be described. For

a

valve, use a

quasi-

steady

description of the

flow through it, based

on Bernoulli's equation

qn,:

A"1/2gh" where A" is

the effective

area

of

the

valve

and is equal to

CuA,.

A" is the

area

available

for flow through the

valve

and C6 is the coefficient

of discharge for

this

area. q"

is the flow

through the

valve

and

h,is the

head

just

upstream of the

valve.

Strictly ft, should be the total head, i.e. the

pressure

head

plw plus

the kinetic energy

head

u2l2g but

in most

pipelines

the

velocity

head term

is so small in

comparison

with

the pressure

head that it is

permissible

to ignore it.

Therefore

A

Di=?

l/Lsh,

where

1o is the

pipe

cross-sectional area,

and hris

the

value

of

hu

at instant

i

but

A

uo:

?

t/2gho.

tap

So

t); A"

lh,

A--E"Vr'"

Denote

A"!A"n

by

n

ana

lkth

by

(

which

are the same symbols as those

employed

by Allievi. Then

!

:

rl{,.

Us

Substituting these

symbols

in

the interlocking equations,

Sec. 2.11

Analytic methods

h,

*h,-,

-)

-.cuo

(u,-r-

9\

ho' ho

-

Slro

\

uo uo/

51

e?

+C?-r- Z=Zp(q'-rC-r

-

t,{,)

where

p:

cudlghs.

These

are the interlocking equations

of Allievi for the case

of

a closing-opening

valve.

Using the techniques demonstrated above,

different

boundary conditions

can

be substituted

both upstream and downstream

and

solutions obtained.

Even

networks

can

be solved

by this method.

Reflectance

and transmittance

coefficients

can

be derived

for such

boundary

conditions as

junctions

and for even more

complicated

circumstances. Even so these devices

solve

problems

which are not

very

closely related

to reality because of the limiting nature

of the

assumptions

that had to

be

made

initially to

reduce

the original equations to

a state in

which the

Von

Riemann

[2]

solution

could be obtained. For

this reason it is suggested that

this

technique

of solution should

not be

considered as accurate. Also,

as

friction is

omitted from the analysis, such methods could not

produce

accurate results

anyway

unless

the

system

is of a high

pressure

type in which

low

velocities

are

present.

The

supply

pipework

of

a Pelton

wheel

hydropower plant

is of such

a type but

most

systems

are not; another

technique

of analysis is required. Even

so,

the

Allievi

interlocking

equations

demonstrate a

great

deal about the nature of waterhammer

and how waves

travel up and down

pipes,

reflecting differently at different boundary

conditions.

For

simple

pipelines,

slow

valve

closures can be

very

easily

solved

without

recourse

to

graphical

or

computing methods.

On the occasions for

which this

is sufficiently

accurate

it could

be a

method

of choice.

2.3.2

Solution of the

Allievi

[3]

interlocking

equations

The solution

of the

Allievi interlocking

equations is a matter of the

utmost

simplicity.

Initially when

the

valve

is fully

open

(say)

the

value

of

rlo:1

and

(o:L;

so

e?

-

t:Zp(l

-

q(r)

where

p

-

cudLghs and

q1

must be known

and specified.

So

a

quadratic

in

(,

results. Having

solved

(.,

the next

stage

of the analysis can be

undertaken.

q2

is known

and

so

the following

equation is obtained:

CZ

+

e?

-

2

-

Zp(rtrh

-

\ze).

Again,

this is a

quadratic

in

(,

with

all other constants known.

So

6,

can be found

and

the process

can then

be repeated for as many multiples

of

las may be required.

Then

and

Ur

:

Uolr(

r,

U2:

Uo\zez,

Us: Dons(3,

etC.

52

The Altievi

interlocking

equations

and

graphical

methods

hr:

hoe?, hr: hne\.,

h3:

hn(!, etc.

lch.

2

The

solution

of

a frictionless

flow

through a

pipeline

with a slowly

closing

valve has

fl,,,o Loa- ^hfoi-arl hrrt if mrrcf hp ramarnhcrerl thof fhe rccrrlt is nnlv reallv accrtrate

ltluat

uvvrr

vuLqlrlvu

uuf tr rrrsor vv

^ --__J

when the

wave

speed

is

very much

greater

than the

pipeline

velocity, and this

velocity

is itself so small

that

the friction

losses can be

regarded

as

negligible'

2.4.1

Graphical

methods

Graphical

methods are based

on

the

Von Riemann

equations

and so

suffer

from the

same limitations

as do the

Allievi

[2]

interlocking

equations,

except

that

friction

does

not

have

to be

neglected.

It

is

possible

to make a

reasonably

good allowance

for friction effects

in

graphical

methods

which cannot be

done

using

the Allievi

[2]

approach. So,

if

wave

speeds

are

high,

so

that

the convective

terms can

be

ignored, the

graphical methods

can

give

good

results.

This is still

a

major

limitation

as

will be seen

in later chapters.

To

develop a

graphical

method

to solve

a simple

pipeline,

three

circumstances

must be represented,

as follows.

(1)

A representation

of

the

behaviour

of

the upstream

boundary

condition.

(2)

A representation

of

the

wave

passing up and

downstream in

the

pipeline.

(3)

A

representation

of the

behaviour

of the

downstream boundary

condition.

We

now examine

these

three

representations

separately.

For the

upstream

boundary

condition

in the case of

a

simple

pipeline this

will be a

reservoir. A

reservoir

must

have the

property

that it

applies a constant

head to

the

upstream end

of

the

pipeline,

irrespective

of the

flow that is occurring

in

it. At this

point

it

is necessary

to remember

that

there

may be many

different

upstream

boundary

conditions

and

that

the

reservoir

is merely

the

easiest

example

to use

to

illustrate how

to represent

an upstream

boundary

condition.

The

graphical

representation

of a

reservoir

is a straight

line set

at a

height of.

H

above the

q

axis

(Fig.

2.2).The

graph has axes

of

-FIand

q.

(Some

other

texts

use

,FI

h

ho

Fig.2.2.

Sec.2.11

Analytic

methods

53

and

u.) The

author does

not consider this

second

alternative

as useful

as the Fl

versus

4

presentation,

because techniques

based upon

it

require an individual

analysis

for

each

pipe,

whereas

the H versus g graph

requires

only

one

sheet of

paper

and

contains

the

complete analysis.

Irf^--r rL- L^---l ):L:^-

-1

-r^-

)^-----t',-- -.-- - .- J -f rr- -

'

t'

r\E^r,

rutr

uuuuualy

surrqruuil ar 1Ir9 sownsLfeam

en(I oI

Ine prpellne

wlu

De

assumed

to

be a

valve.

Again,

this is because the valve

is

one of

the

simplest

possible

boundary

condition to analyse

and

so is a

good

illustration

of how

to represent

such

boundary

conditions in a

graphical

manner. Applying

Bernoulli's equation

across

a

valve gives

q:

A;,@h

where

A":

CAu

and

A, is the

valve

flow

area.

So

,q2

n:

zgAz

'

This is

the

equation of a

parabola.

As the valve

closes,

the

area

changes;

so at

T(:ZLlc)

intervals

there

are

varying values

of. A":

17,27,3T,47,

...,

A"r, 4.., A"r,

A.o,

'..

and, if

the valve

is closing, A

"

diminishes and, if it

is opening, .4

"-

increases

;

it is

even

possible

to analyse

an oscillating valve.

So

,q2

fi7-

2sA?'

This

equation

can be

written

as

h

=

ryqz;

the function

y

varies for

each

value

of A"

and

so there

is a

parabola

for each time

value

:

iT (T

-ZLlc

and i

is any one of the

integer

multipliers describing

the duration

of the closur

e

t

,

2, 3

,

4

,

.. . . Thus

a

plot

of

all

these

parabolae

consists of n

parabolae

each specified

by

its

ry

number.

(Fig.

2.3).

Consider

the

wave representation.

The wave

equations are

h=ho+r(r+.,.(,-:)

,

u:uo

-i-["('4-4'

:)]

54

The Allievi interlocking

equations

and

graphical

methods

lch.2

Consider a wave travelling at velocity

c along a

pipe.

If such a wave is at a

point

X

at a time I,

then at another time f the wave will

be at

a

point

x

given

by the equation

(x

-

X)l(t

-

T):

*

c where

the

plus

sign applies if

the

wave

is travelling in the

direction

of .r increasing

(the

downstream direction)

and the minus

sign applies

when

the

wave

is travelling

in the direction

of x decreasing

(upstream).

Now consider an

observer

(a

waverider)

who is travelling with

the

wave

and at the same velocity; his

equation

will

be the

same as that of the

wave,

i.e.

x

=

X

*

cQ

-

n.Considering

the

waverider

who

is moving upstream

first, the F(t+xlc)

expression becomes F{t+

[Xlc

-

(t

-

Dl]

which

equals F(T + Xlc) and

this is the constant magnitude

of

the

wave

that the waverider will

observe. If

the same

waverider

travelled downstream,

he

would

meet the

same F

waves

coming upstream

but they

would

have

varying

magnitudes

F{r +

lXlc

+

(t

-

f)l}

,i.e.

F(Zt

-

T + Xlc)

as he

would

then be travelling

through the

waves

and

not

with

them.

When

the waverider

travels downstream,

he

will

encounter

/

waves

travelling

with

him and

these

will

have constant magnitudes/{t-

lXlc+

(r-

Dl}

i.e.

f(T-

Xlc), but

should he travel upstream

the

/(t

-

xlc)

wave will

appear

to have a

magnitude

of.flZt

-

T+ Xlc),

i.e. a

variable

magnitude.

Keeping

the above

results

in mind,

examine the

head

and velocity

equations

written for

two

points

on the

pipeline.

Writing

the

head

equation

for the

X, Z

position

of the

wave

gives

Sec.2.1l Analytic

methods

Subtracting the head equations,

h*,r-

h,,,

but, for an

observer travelling upstream,

as F(I +

Xlc)

:

F(t + xlc) and

f(t

-

xlc):

f(zt

-

T + Xlc)

from before, we have

h*,r-

h,.,

writing

the

velocity

equations

for the two

positions,

55

D,,t:rr-too(r.,

-(t

,]

again subtracting,

h,,,: n"+ n(t.i) .t(r-,

:r(r+

:)

r(,+,.(

r-u)-r(,-,

:r(,-:)-4"-,*{)

,,x,r:

u,-tl"(..f)

{r-f)]

::[4

,-n)

-r(,,-'.f)]

hx,r:n"+

r(r+f) .{ r-:)

It

will

be seen that

the

term on the right-hand

side in square brackets is the

same

as

the corresponding

term in

the head

equation

just

developed above.

Therefore

h*,,

-

h,,,

:

itr-,

r

-

u,,,).

rf

parabolae

Fig.2.3.

'|)x,r-u',,::["('.,

-4'-, -n(r+f)

.(.

tJ]

and

making the

same

substitutions as were made

above, then

ux,T- D',,

For the

x,

r

position

the equation is

Fox J.A. Transient Flow In Pipes, Open Channels And Sewers

Подождите немного. Документ загружается.