Фотиади Э.Э. (ред.) Геология и математика
Подождите немного. Документ загружается.


218
Гдава
/V.
Сn
е
циадьnые
meop
emu.,ecl>ue
в
опросы
те
результаты,
которые
были
изложены
в
главе
111,
а
также
пересмотреть
понятие
«залежи
полезного
ископаемого»,
толко
вание
факта
обнаружения
«залежи
полезного
ископаеМОГQ»,
"Толкование
процедур
(<ПодсчеТа»,
определения
«категорийности
и
нормирования
запасов
полезного
ископаемого»
результаты
по
выбору
«рациональной
разведочной
»
сети.
Некот
о
рые
момен
"ТЫ,
связанные
с
таким
пересмотром,
которые
уже
аатрагивались
в
работе
[24],
мы
обсудим
далее
.
Сейчас
же
ограничимся
обсуждением
одной
модельной
поисковой
задачи.
Положим,
что
в
нашем
распоряжении
име
ются
одинакового
формата
ящики,
в
которые
плотно
вложены
по
(i
+
1)
листу
фанеры.
Будем
считать,
что
1-й
лист
фанеры
разрезан
на
k
частей,
2-й
-
на
k
2
частей
и
т.
д.
до
i-ro
листа,
который
разрезан
на
k
i
частей.
Разрезы проведены
так,
что
k
частей
l-ro
листа
составляет
одну
часть
(l -
1)-ого
листа.
Под
каждой
частью
i-ro
листа
на
(i +
1)-ом
листе
вырезано
отвер
.стие,
куда
можно
заложить
одну
фишку
.
Будем
считать,
что
фишки
могут
быть
т
сортов.
Положим,
что
каждый
р-ый
из
n
заготовителей
эталонных
ящиков
имеет
право,
по
своему
'усмотрению
,
окрашивать
каждую
из
частей
листов
фанеры
в
одну
из
qp
красок
и
закладывать
r
р
фишек.
По
каждому
Р-ОМУ
эталон
ному
.
ящику
изготовляется
Sp
его
образцов.
Всего
в
нашем
рас-
n
поряжении
оказывается
S =
~S
p
ящиков
.
Для
того
чтобы
из-
Р
=
l
влечь
какую-либо
фишку
из
любого
ящика,
необходимо
выта
щить
из
него
не
менее
i
частей
л
истов
фанеры.
Положим
,
что
'
стоимость
вытаскивания
одной
части
l-ro
листа
фанеры,
неза
висимо
от
раскраски,
равна
а/.
Спрашивается,
мо
ж
но
ли
ука
.
зать
алгоритм
,
который
гарантирует
извлечение
из
S
ящиков
всех
фишек
и
ноторый
минимизирует
затраты
на
такое
извле
чение?
3.
Задачи
(<подсчета,
определ
е
ния
категори
й
ности
и
нор
мирования
запасов
полезных
ископа
е
мых»
рассматриваются
уже
много
лет
[47].
ИзвеС1
·
ные
решения
этих задач
с
теоретичес
ких
и
практических
позиций
не
признаютсясейчас
удовлетво
рите л
ьными
[3,13,15,106].
Если
обратиться,
например,
к
нефти
и
газу,
то
можно
выяснить
следующее.
Анализ
последне
й
ин
струкции
ГRЗ
[38]
пока
з
ывает
,
что
разделение
з
апасов
нефти
и
га
з
а
на
(<промышленные»,
(<перспы<тивные
»
и
(<прогнозные»,
а
так
же
выделение
категорий
А,
В,
С
1
,
С
2
И
групп
D
1
,
D
2
проводится
С
чисто
описательных
позиций.
Можно
убедиться,
что
раз
л
ичные
форму
л
ы
подсчета
запасов
н
е
фти
и
газа
по
кате
.гориям
А
,
В,
С
l '
связанные
с
«объемным
»
м
е
тодом
,
методом
(
<К
ри-

§ 4.
К
теории
поиска
219
вых
падения
дебитов
и
давлений»,
методом
«материального
ба
ланса
углеводор
о
д
о
в»
[35],
являются
чисто
эмпирическими
и
для
всех
этих
формул
сейчас
нельзя
указать
области
применимости
и
нельзя
дать
оценку
их погрешности
.
Известно
,
что
для
кате
гории
С
2
и
групп
D
l
,
D
2
по
·
нефти
и
газу
нет
сколько-нибудь
об
щепринятых
способов
подсчета
запасов
[34, 44, 57, 65, 67].
Что
же
касается
задачи
нормирования
запасов
нефти
·
и
газа,
то
она
до
сих
пор
не
имеет
однозначной
трактовки
[30, 50, 96, 97,
98].
В
связи
с
этим
,
как
известно,
существует
значительный
произвол
в
определении
категорий
и
rруiIП
запасов
нефти
и
га
за,
допускаются
неконтролируемые
ошибки
при
подсчете
запа
сов
этих
полезных
ископаемых
по
любым
категориям
и
группам
;
существует
значительный
произвол
в
нормировании
запасов
нефти
и
газа.
По-видимому,
отмеченные
недостатки
в
значительной
мере
связаны
с
отсутствием
формального
определения
понятия
«за
лежи
полезного
ископаемого
»
,
отсутствием
формального
толко
вания
факта
обнаружения
«Залежи
полезного
ископаемого
»
,
что
не
позволяет
корректно
сформулировать
задачи
по
подсчету,
определению
категорийности
и
нормированию
запасов
полезных
ископаемых
с
учетом
геологических
и
ЭI
<
ономических
требова
ни
й
(в
частности,
неравноценности
ошибок
в
сторону
завышения
и
в
с
торону
занижения
запасов
полезных
ископаемых)
.
Естественно, что
попытку
внести
хотя
бы
некоторую
ясность
в
вопросы
подсчета,
определения
категорийноети
и
нормирова
ния
запасов
пол
е
зных
ископаемых
следует
начинать
с
рассмот
рения
достаточно
.
простого
моде
л
ьного
примера,
и
з
бегая
по
воз
можности
применения
ка
к
их-
л
ибо
с
л
о
ж
ных
математических
конструкци
й
.
4.
Рассмотрим
отрезок
[-h,
h]
прямой
Х
.
Предположим,
что
в
некоторых
точках
Xi
внутри
[- h,
h]
проведены
измерен
и
я
значений
функций
(4.4.
1)
Будем
сч
и
тать,
что
выбраны
неноторые
проц
е
дуры
интерполя
ции и
экстраполяции,
за
счет
которых
на основе
(4.4.1)
можно
построить
совокупность
функций
<Pl
(Х),
<р
2 (
х
),
..
. ,
<Ps
(
х
),
х
Е
[-
h, h).
(4
.4.
2)
Буд
е
м
предполагать
,
что
любая
<р,
(
х
)
из
(4.4.2)
является
почти
всюду
непрерывной
в
[-
h,
h]
.
Испо
льз
уя
(4.4.2) ,
проведем
элементаризацию
[-
h,
h]
(глава
III,
§ 5,
п
.
2),
что
позволит

220
Гдаlfа
/У.
Сnециадьные
meореmuчеСl>uе
IfОnРОСЫ
разбить
[-
h, h)
на
такие
участки,
внутри
которых
любая
q>
i
(X)
из
(4.4.2)
будет
непрерывной.
Установим
на
основе
(4.4.2)
некоторую
процедуру
описания
полученных
участков
(напри
мер,
по
средним
значениям
q>
i
(Х)
из
(4.4.2).
На
множестве
полу
ченных
участков
определим
некоторую
систему
признаков
U
(глава
II,
§ 1,
п.
3),
на
основе
которой
построима-классифика
цию-переqисление
участков
(глава
II,
§ 2,
п.
2).
Отметим,
что
в
U
могут
входить,
в
частности,
и
признаки,
связанные
с
поло
жением
участков
относительно
некоторых
фиксированных
то-
.
чек
х".
Условимся
через
а
обозначать
участки,
через
l
(а)
-
их
длину,
через
А
-
множество
участков.
Разделим
А
на
два
под
множества
А
+
и
А
-
таких,
что
l
(а)
>
lo,
если
а
Е
А+,
и
l
(а)
<
<
lo,
если
а
ЕА
-.
Разделим
А
+
на
такие
два
подмножества
A~
и
A~,
что
в
А1
входят
те
а,
которые
находятся
целиком
в
[О,
h),
а
в
A~
входят
все
другие
а
Е
А
+.
Рассмотрим
аЕА
+.
Такие
а
можно,
во-первых,
занумеровать
+
слева
направо,
во-вторых,
каждому
такому
а
приписать
номер
класса,
используя
[А
:
и]
(глава
II,
§ 2,
п.
3).
Таким
образом
,
каждому
а
Е
А1
можно
приписать
символ
а
(а,
~),
где
а
-
це
лое
число,
характеризующее
положение
а
внутри
[О,
h],
а
~
целое
число,
характеризующее
класс
из
[А:
и),
к
которому
принадлежит
а.
Пусть
почти
всюду
непрерывная
в
[-
h, h)
функция
р
(Х)
отвечает
плотности
запасов
полезного
ископаемого
р в
[
-h,
hJ.
Будем
предполагать
,
что
р
(х)
в
[ - h,
h]
согласна
·
с
(4.4.2)
(глава
III,
§ 3,
п.
11):
если
р
(Х)
в
некоторой
точке
х'
Е
[-h,
h)
терпит
разрыв
непрерывности,
то
всегда
найдется
по
крайней
мере
одна
такая
ср
;
(Х)
из
(4.4.2),
которая
тоже
терпит
разрыв
непрерывности
в
х'
Е
[-
h,
h).
Это
гарантирует
непрерывность
р
(Х)
внутри
выделенных
участков
24).
Предполо
ж
им, что
в
[О,
h)
выбрано
N
точек,
которые
явля
ются
внутренними
по
отношению
к а
Е
А1
и
в
которых
были
про
ведены
измерения
р.
Каждому
а
(а,
~)
Е
А
1
можно
сопоставить
l(a,~)
-
длину,
N
(а,
Ю-число
точек,
в
которых
были
проведены
измерения
р
,
числа
x1(a
'~)'X
2
(a
,~),
...
,
Х Щх,
ю(а
,~),
отвечающие
ко-
. :
2~
)
Добиться
непрерывности
Р
(х)
можно
иным
путем.
Если
Ро
(х)
плотность
запасов
в
[-h,
h],
то
можно
ввести
среднюю
=
плотность
з
апа
СОв
1
х+а
р
(х)
=
а ~
Ро
(х)
ах.
х

§
4.
R
теории
noиc~a
221
ординатам
точек
измерений
Р
в
а
(a,~)
Е
А
~
,числа
Р1
(а,
~),
Р2
(а,
~),
...
,
PN
(/X,fj)
(а,
~),
отвечающие
результатам
измерений
р.
Введем
параметр
N
«(1.
,
~)/l«(1.,~)
=
N°
((1.
,
~).
Используя
этО1
'
параметр,
разобьем
A~
на
два
подмножества
A
~
(1)
и
A~
(2),
предполагая,
что
для
а
(а,
~)
Е
А
1
(1)
выполнено
N°
(а,
~)
;;;;.
;;;;.
n(а,
~),
а
для
а
(а,
~)
ЕА
1
(2)
выполнено
N°(a.
~)
< n
(а,
~).
Множество
участков
A~
(1)
назовем
множеством
экспери
ментально
изученных
по
р
(х)
участков.
Для
каждого
а
(а,
~)
Е
A~
(1)
на
основании
Х
;
(a,~)
и
Pi
(а,
~)
можно
получить
отношения
1 Pi
(1%
,
~)
-
Pk
(1%,
~)I
=
б
«
(1.
~)
, lxi(I%,
~)-xk(l%,
~)I
1,
(4.4.3)
i
=F
k,
i,
k = 1, 2,
...
, N
«(1.,
~)
,
которые
характеризуют
перепады
р
(х)
в
а
(а,
~)
Е
A~
(1)
на
еди
IШЧных
интервалах.
Для
совокупности
а
(а,
~)
Е
A~
(1),
отвечающей
различным
значениям
а
и
фиксированному
значению
~,
можно
построить
статистические
ряды
по
р
Pi
(~)
,
У
;
(~),
i = 1, 2,
...
, n
(~),
(
4.4.4
)
и
по
б
б
;
(~),
'I't
;
(~),
i =
(2,
.
..
,
т
(~).
(4.4.5)
Здесь
Р
;
ф) И
б
;
(~)
-
значение
плотности
запасов
полезного
ис
копаемого
и
значение
перепада
этой
плотности
на
единичном
ин
тервале,
вычисляемые
с
помощью
некоторых
дискретных
шка
J
I
для
Р
и
б,
а
Yi
ф)
И
'I't
;
ф)
-
их
эмпирические
частоты.
Исходя
из
(4.4.4),
можно
вычислить
среднюю
плотность
за
пасов
полезного
ископаемого
Р
для
любого
~
-го
класса,
предста
вленного
в
A~
(1),
n
(l!)
р
(~)
=
~
Yi
(
~)
Р
;
(~).
i=1
(
4.4
.6)
Назовем
а
квазизалежью
полезного
ИСJ{опаемого
р.
есл
и
а
Е
А
~
(1)
и
если
а
относится
к
такому
классу
~,
представ
ле
нному
+ -
в
А
+
(1),
для
которого
в
СООТDеТСТDИИ
с
(4.4.6)
имеет
место
Р
(~)
;;;;.
;;;;.
Ро
(~)26
) .
~)
т
аки
ы
образоы
'
Bыстоo
залежи
полезного
ископаеыго,'
к
о
торан
обычно
то
л
куе
тс
я к
а
к
область
,
где
плотность
запасов
полезного
ископае
мого
превышает
некоторую
ко
нстанту,
вводится
кв
азиза
лежь.
Это
СDЯ-

22
2
Гдава
IV
.
сnециадыiеe
mеореmи1{еские
во
просы
Опираясь
на
(4.4.4),
для
каждой
квазизалежи
а,
принад
лежащей
к
~-MY
классу,
можно
определить
постоянные
p~
(~)
и
p~. (~)
такие,
что
эмпирические
вероятности
событий
Р
а
<
p~
(~}
ИРа
>
p~.
ф),
где
Ра
-
плотность
запасов
полезного
ископаемо
го
Р
внутри
а
,
будут
меньше
наперед
заданной
величины.
Используя
(4.4.5),
для
каждой
квазизалежи
а,
принадле-
·
жащей
к
~-классу,
можно
определить
постоянную
СО
ф)
такую,
что
эмпирическая
вероятность
события
ба
>
СО
ф),
где
б
а
-
перепад
Р
на
единичном
интервале
внутри
а,
будет
меньше
вы
бранной
величины
.
Постоянные
(4.4.
7)
.
условимся
называть
граничными
параметрами
~-oгo
класса
ква-
·
зизалежеЙ.
5.
Под
обнаружением
квазизалежи
полезного
ископаемого
Р
в
[
-h,
О]
будем
понимать
процедуру выделения
в[-
h,
О]
за
счет
элементаризации
[-
h,
О]
по
(4
.4.2)
некоторого
участка
а
и
установление
факта,
что
данный
участок
а
является
квази-
·
залежью
26).
6.
Пусть
обнаружена
квазизалежь
а
полезного
ископаемого
Р,
которая
относится
к
~-OMY
классу
таких
квазизалежеЙ
.
Под
запасами
полезного
ископаемого
Р
n
а
будем
понимать
х,
(а)
р
а
=
~
Р
(
х
)
ах,
(4
.
4.8)
~
х,
(а)
где
x1(a),
Xz
(а)
-
граничные
точки
а.
При
построении
оценок
:
для
(4
.4.8)
будем
опираться
на
(4.4.
7)
и
возможность
проводить
измерепия
Р
внутри
а
снекоторой
погрешностью.
У
словимсл;
(4.4.7)
толковать
как
априорные
сведения
об
а,
а
результаты
из-
о
мерений
Р
внутри
а
-
как
апосториорные
сведения
об
а.
Кроме
-
\
зано
с
тем,
что
привычнеe
толкование
зал
е
жи
полезного
ископаемого
не
позволяет
конструктивно
истолковать
факт
обнаружения
залежи.
ДеЙ-
·
ствительно,
если
исходить
из
принятого
определения
залежи,
то
ее
обна-
·
ружение
предполага
е
т
установление
факт
а,
что
во
всех
точках
.
данноЙ
·
области
плотность
з
а
пасов
превышает
некоторую
константу.
Это
крайне
неудобно
.
В
известном
смысле
,
понятие
квазизалежи,
положим,
н
е
фти
.
и
газа
будет
эквивал
е
нтно
и
с
пользуемому
сейчас
понлтию
ловушки
нефти
и
газа.
26)
Таким
образом,
само
определение
квазиз
але
жи
ОI(
а
зывается
су-
щественно
зависящим
от
экспериментального
опыта
в
[О,
h),
а
ее
обнару-
·
жение
в
[-h,
О)
также
толкуется
на
основе
эксперим
е
нтального
опыт
а..
в
[О
,
h).

§ 4. R
теории
noucn:a
223
того,
к
априорным
сведениям
об
а
отнесем
постоянную
Р
О
ф),
которая
позволяет
при
Р
а
:>
Р
о
(~)
считать
а
балансово
й,
а
при
Р
а
<
Р
о
ф)
считать
ее
забалансовоЙ.
7.
Результаты
измерения
р в
некоторой
т
о
чке
х'
Е
(хl
(а),
Х2
(а»
условимся
толковать
как
задание
р*(х')
и
р**
(х
'
)
таних,
что
р.
(
х
')
<
р
(
х
')
<
р
••
(
х
').
(4.4.9)
'~'-словимся
считать,
что
измеренное
значение
р
(х')
можно
оп
ределить
так:
ри
з
м (х
'
)
= ;
[р.
(
х
')
+
р
'.
(х')].
(4.4.10)
Предположим,
что
выбраны
места
для
заложения
1-й, 2-Й,
...
...
,
k-ойточек
,
вкоторыхпроведены
измерения
(процедуру
выбора
мест
заложения
этих
точек
измерения
пока
оставим
в
стороне).
Тогда,
зная
координаты
точек
измерения
и
используя
резуль
таты
измерения,
можно,
во-первых,
за
счет
перестройки
статис-
·
тических
рядов
(4.4.4)
и
(4.4.5)
получить
вместо
(4.4.7)
р;
(~),
р;.
(~),
С;
(~),
i =
1,2,
...
, k, (4.4
.11)
во-вторых,
построить
оценки
(
4.4
.1
2
).
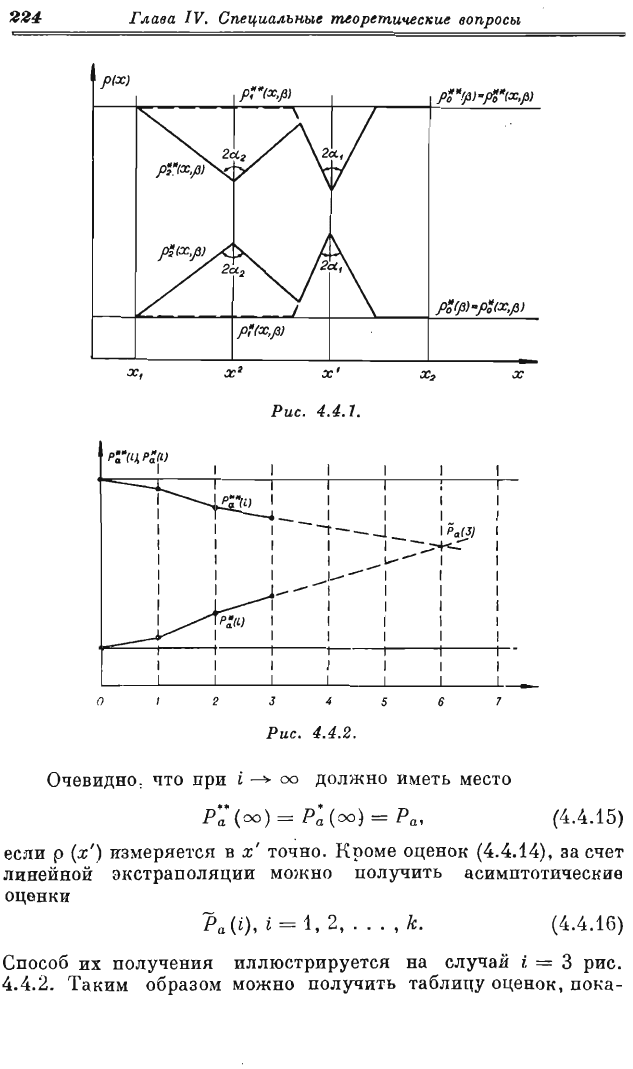
Способ
построения
этих
оценок
иллюстрируется
рис.
4.4.1,
г
д
е
1 1
tg
а
1
=
Со
(lЗ)'
tg
а2
=
Сl
«(3)
•
Исходя
из
(4.4.12),
можно
для
Р
а
из
(4.4.8)
получить
оценки
где
Р:
(i)
<:
Р
а
<
Р:·
(i), i =
О,
1,
2,
...
, k, (4.4
.1
3),
х,
(
а
)
Р:'
(i)
=
~
р;' (х,
~)
ах,
х
,
(а
)
х,
(а)
Р:
(i) =
~
р; (х,
~)
ах.
х,
(а)
(4.4
.1
4)1
(4.4
.1
4)2
Можно
убедиться,
что
оцеНl{И
(4.4.13)
являются
монотонными
кусочно-линейными
функциями
от
i.
При
этом
(4.4.14)1
являет
ся
невозрастающей,
а
(4.4.14)2 -
неубывающеЙ.
Характер
этих
функций
иллюстрируется
рис.
4.4.2
27
).
27)
ер.
с
рис.
XXXV,
1,
сТр.
631
[89].
Глава
lУ.
Сnециальн,ые
meоретичеСlf:ие
вопросы
х,
х'
х'
х
Рис.
4.4.1.
, ,
, , 1 1
--"--...1
1;;.(3) 1
,
,--:....~,
1
"",--,
1
,------,
, ,
----
1 , , ,
, 1 , 1
1 , , 1
1 1 , ,
, 1 1 , -
, , 1 ,
, ,
1-
о
2
3 4 5 6
Рис.
4.4.2.
Очевидно
,
что
при
i --'>-
00
должно
иметь
место
Р
:·
(
00)
=
Р
:
(оо)
=
Р
а
,
(4.4.15)
если
р
(х')
измеряется
в
х'
точно.
Кроме
оценок
(4.4.14),
за
счет
линейной
экстраполяции
можно
получить
асимптотические
оценки
Pa(i), i =
1,2,
...
, k.
(4.4.16)
Способ
их
получения
иллюстрируется
на
случай
i = 3
рис.
4.4.2.
Таким
образом
можно
получить
таблицу
оценок,
ПОRа-

§
4.
К
теории
nОU
СIЩ
22
/$
з
анную
в
табл.
4.4.1.
Исходя
из
знания
постоянно
й
Ро
(М,
мож
но
указать
решающее
прави
л
о
дл
я
опр
едел
ения
балансов
ости
I<
вазизалежи
а
полезного
ИСI<опаемого
р.
Е
сли
при
некотором
i'
,
О
<
i'
< k,
ОI<а
же
тся,
что
Т
абл ица
4.4.1
(4.4.17)
то
а
следует считать
балансовой.
Есл
и
ж
е
ОI<ажется
,
что
p
~
.
и')
<
Р
О
(~)
,
(4.4.18)
то
а
сле
дует
с
читать
забалансо
в
ой.
Мож
ет
ОI<азаться,
что
при
0<
i' < k
ни
(4.4.17),
ни
(4.4.18)
не
реализуется.
Тогда
тр
ебуется
у
величение
числа
точек
и
зм
ере
ний
р
.
8.
посI<о
лы<y
процед
ура
по
с
т
роения
оценон
для
(4.4.8)
зави
Р
а
* (О)
Р
а
*
(1)
Р
а
*
(2)
. , .
Р
а
*
(k)
I
Р
а
**
«
()
) I
-
I
Р
а
**
(1) I
Р
а
(1)
I
Р
а
*
*
(2) I
Р
а
(2)
I
...
I
. ..
I
Р
а
**
(k) I
Р
а
(k)
с
и
т
не
толы<o
от
числа
точеI<
измерений
р,
но
и
от
мест
рас
по
ложения
этих
точеI<,
следу
е
т
рассмотреть
с
пособ
выбора
ме
с
та
распо
лож
ения
(k +
1)-ой
ТОЧI<И
измерения
р.
Испо
льзу
я
(4.4.12),
обозначим
~P
i
(х,
~
)
=
р;.
(
х
,
~)
-
р;
(
х
,
~
),
и,
привлеI<ая
(4.4.11),
поло
жим
Llpi-1
(~)
=
P:~1
(~)
- P;-l
(
~
).
(4.4.20)
О
пределим
ко
э
ффици
ен
т
изученности
р в
точке х
Е
(хl
(а),
Х2
(
а
»,
п
ри
наличии
i
точек
измер
ений
р
в
(хl
(а),
Х2
(а»,
формулой
(г
лава
IIJ,
§
12
;
п.
2)
(
)
1
~P
i
(х
.
~)
(4
1,
21)
'fJ
i
р,
х
= -
~Pi-l
(~
)
• . i .
П
од
средним
коэффициентом
изученности
в
(Х
1
(а),
Х2
(а»,
при
н ал
ичии
i
точек
измерений
р
в
(Х
1
(а),
Х2
(а»),
будем
понимать
х
, (
а)
- 1
('
'fJ
i
(р,
Х
)
=
Х
2
(а)
_
Xl
(а
)
J
'fJi
(р,
х
)
ах,
х
,
(
а
)
(4.
4.22
)
с
о
ответствующий
минимальный
коэффициент
опреде
лим
так:
~
i
(р,
Х)
=
min
'fJ
i
(р,
х
),
(4.4.23)
х
Е
(х,
(а
)
.
х, (а
»
15
ГеО
Л ОГИ
fl
и
математик
а

226
Глав
а
IV.
Сn
е
ц
uал
ьn
ы
е
mеореmuчеС1Сuе
вопросы
а
соответствующий
максимальный
коэффициент
определим
та
к
:
~
i
(р,
Х
)
=
тах
'l']
i
(р,
х).
(4.4.
24
)
х
Е
(х,
(
а
),
х
,
(
а
»
Используя
(4.4.21),
определим
в
(Х
1
(а)
,
Х2
(а»,
связные
подмно
же
ства
точек
Х
1
,
Х
2
,
",
X
r
,
на
которых
'l']k
(рх)
достигает
минимума.
Из
Х
l'
Х
2
,·
••
, X
r
выберем
X
q
такое,
что
1
(X
q
)
=
тах
1
(Х
;
).
i = 1, 2,
...
, ,.
Тогда
место
заложения
(k +
1)-ой
точки
измерения
р
можно
будет
определить
как
геометрический
центр
X
q
•
(Если
q
прини
мает
несколько
значений,
то
можно
произвольно
выбрать
одно
И3
них.)
28)
Процедуру
выб
о
ра
места
заложения
(k +
1)-ой
точки и
з
ме
рения
р
можно
ИСПОЛЬЗ0вать,
начиная
с
k =
О.
Эта
процедура
приведет
к
построению
разведочной
сети,
которая
будет
опти
мальной
в
том
смысле,
что
она
гарантирует
максимальные
зна
чения
для
(4.4.22)
и
минимальные
разности
между
значениями
(4.4.24)
и
(4.4.23).
9.
Может
оказаться,
что,
·
несмотря
на
выбор
оптимальной
разведочной
сети
и
привлечение
з
начительного числа
точек
И3-
мерения
р,
ни
(4.4.17),
ни
(4.4.18)
не
реализуются.
ТОГД<i
можно
ВОСПОЛЬЗ0ваться
оценками
Р
а
(i).
Положим,
что,
например,
оценки
Р
а
(k - 2),
Р
а
(k -
1)
и
Р
а
(k)
отличаются
между
собой
незначительно
29),
тогда
в
(4.4.17)
или
(4.4.18)
можно
заменить
p~
(i)
или
р
.;
(i),
например,
на
Р
а
(k).
10.
Предположим,
что
для
выбранной
квазизалежи
а
по
лезного
иекопаемого
р
после
заложения
k
точек
измерения
р
реализуется
(4.4.17).
Тогда
встает
задача
оценки
Р
а
таким
об
разом,
чтобы
относительная
ошибка
в
сторону
завышения
запа
·
·
сов
а
не
превысила
некотор
о
го
фиксированного
числа
процента
u
(~).
В
качестве
расчетного
запаса
естественно
принять
-
1·
· •
Р
а
="2
[Р
а
(k) +
Pa(k)],
(4
А
25)
28
В
действительности,
н
а
случай,
когда
области
Xi
не
являются
одномерными,
выбор
м
еста
з
алож
ения
(k
+
1)-ой
точки
измер
ен
ия
р
сводится
К
решению
такой
з
а
д
а чи.
Пу
с
ть
G -
открыт
ая
связн
а
я
обл
а
сть,
G -
ее
замыкание,
r =
G/G
-
ее
гр
а
ница.
Расстояние
м
е
жду
точками
а,
Ь
Е
G
будем
обозначать
р
(а,
Ь)
.
Найти
множество
С'
С
С,
удовлетво
ряющ
ее
условию
р
(g',
,\,)
>
d,
где
g'
Е
С'
,
'\'
Е
Г.
29
Отличие
соизмеримо
с
погр
е
шно
с
тью
измерения
р
(
х
)
в
х
Е
(хl
(
а),
Х2
(
а
».

§ 4. R
теории
noucli:a
227
при
этом
сформулированное
выше
требование
можно
будет
за
писать
в
виде
р:'
(k) -
Р:
(k) d
Р:"
(k) +
Р:
(k) <
(~).
с
учетом
(4.4.14)
условие
(4.4.26)
запишется
в
виде
х
,
(
а)
'
••
•
а
а
(k) =
~
p~"
(
х, ~)
-
P~
(х
,
~)
ах
< d
(~).
х,
(
а)
Р"
(х,
~)
+
Pk
(
х,
~
)
(4.4.
26
)
(4.4.27)
Д
л я
реализаци
(4.4.27)
может
потребоваться
зало
жен
ие
допол
нительных
точек
измерения
р.
11.
Будем
говорить,
что
квазизалежь
а
полезного
ископае
мого
р,
для
которой
после
заложения
k
точек
измерений
р реа
лизуется
(4.4.17),
относится
к
категории
А,
если
(4.4.27)
имеет
место
при
dф)
= 0,1,
к
категории
В,
если
(4.4.27)
выполняется
при
a(~)
= 0,25,
к
категории
С
l'
если
(4.4.27)
имеет
место
при
dф)
= 0,5.
12.
Пусть
имеются
квазизалежи
а
1
,
а2
и
аз
полезного
иско
паемого
р,
для
которых
после
заложения
соответственно
k
1"
k
z
и
k
з
точек
измерений
р
реализуется
(4.4.17),
а
условие
(4.4.27)
выполняется
соответственно
при
а
1
(~1)
= 0,1,
а
2
(~2)
= 0.25.
d
з
(~
з
)
= 0,5.
Иначе
говоря,
а
1
,
a
z,
аз
относятся
соответственно
к
категориям
А
,
В,
С
1
И
К
классам
~
l'
~z,
~
з.
Определим
процедуру
нормирования
запасов
в
а
1
•
а2
и
аз
формулой
где
- -
-
Н
-Н
Р
а
,а
2
а
,
=
Р
а
,
+
Р
а
,
+
Р
а
. ,
-
Н,
1
Р
а
•
=
Р
а
,
(k
z
)
1-
0
,1
'
-
Н
• 1
Р
а
,
=
Р
а
•
(k
з
)
1-01
•
,
Il.
J5
а
,
оiIределяется
аналогично
Р
а
'
(4.4.28)
(4.4.29)
13.
Рассмотренная
принципиальnая
схема
подсчета.
опр
е.
деления
категорийности
и
нормирования
запасов
полезных
ис
копаемых.
как
представляется.
отличается
от
известных
схем
[84]
тем.
что:
(1)
опирается
на
формальный
учет
предшествующего
гео
лого-экономического
опыта
(см.
пп.
3, 5);
(2)
основана
па
определении
квазизалежи
поле
з
ного
иско
паемого
теоретико-вероятностного
характера
(см. п.
3);
(3)
базируется
на
формальном
истолковании
процедуры
об
наружения
и
описания
квазизалежи
полезного
ископаемого
в
заданном
формальном
геологическом
пространстве
(см. п.
4);
15·
