Flechtner F.M., Gruber Th., G?ntner A., Mandea M., Rothacher M., Sch?ne T., Wickert J. (Eds.) System Earth via Geodetic-Geophysical Space Techniques

Подождите немного. Документ загружается.

494 M. Mandea et al.

is to co-estimate the Euler angles between the FGM and ASC as part of the modeling

of the geomagnetic ﬁeld. In an attempt to minimize the difference between magnetic

ﬁeld readings and model predictions the three angles are treated as free parameters.

Small values for these angles can be considered in a closed loop validation of the

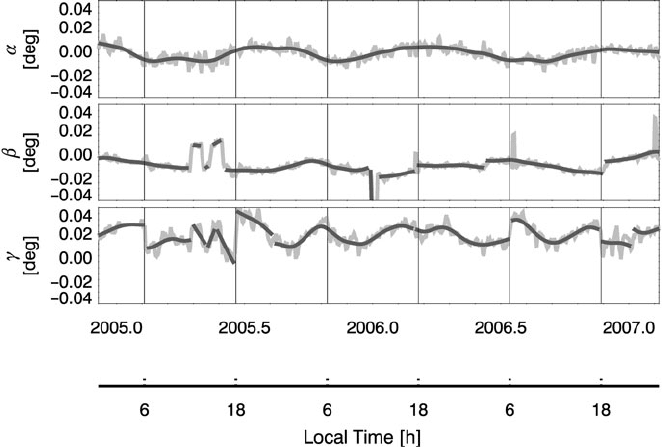
magnetic ﬁeld data in NEC frame. Figure 12 shows a time series of obtained Euler

angle variations of the optical bench for 2005–2007. The three components describe

rotations around the roll, pitch and yaw axis. Variations of order ±0.001

◦

can be

observed, and particularly, the α and γ angles show variations synchronized with

local time. In this context it has to be noted that the estimation of Euler angles

assumes a magnetic ﬁeld which can entirely be described by a scalar potential. For

measurements done into the ionosphere this is not strictly true. The synchronized

variations may therefore indicate that the violation of the assumptions is local time

dependent. There are several jumps in the bottom plot occurring just at dawn and

dusk. This behavior can be explained because only night time data are used for

the magnetic ﬁeld modeling. When the satellite orbit passes the 06/18 local time

sector the considered data set is switched from ascending to descending or vice

versa. Obviously, the magnetic ﬁeld data in the NEC frame are somewhat different

depending on the sampling direction from North to South or South to North.

The angle β shows also some s pikes and deviations. The narrow spikes could

be associated with time errors. At certain intervals the GPS receiver sees only 4–5

GPS satellites. This is not sufﬁcient to generate a reliable time signal. In those cases

Fig. 12 Temporal variations over 2005–2007 of the co-estimated optical bench Euler angles: rota-

tions around the roll (top), pitch (middle) and yaw (bottom)axesareshown.Vertical lines mark the

crossings of the orbital plane through the 06 and 18 local time

The Earth’s Magnetic Field 495

the PPS is off by a fraction of a second. Such a time error has a similar effect as a

wrong pitch angle. Therefore, these spikes appear only in the β angle values. The

large negative excursion in the middle of the frame is associated with the leap second

at the beginning of 2006. Some of developed codes are obviously not able to handle

this situation correctly.

Figure 12 shows the result of Euler angles co-estimation when using a 3-day

interval for ﬁeld modeling. The dark heavy line is a smooth piecewise ﬁtted curve.

Angles derived from this later curve are used to improve the rotation from the FGM

to the ASC system. With this ﬁnal update a set of reliable NEC data processed is

available. Finally, lets us stress that the undulations visible in Fig. 12 cannot be

interpreted directly as variations of the Euler angles. They are the sum of many

small imperfections of data from various instruments. Nevertheless, by applying

these corrections the ﬁnal NEC magnetic ﬁeld data quality is greatly improved.

2.6 Complementarity of the Ground and Satellite Data

Ideally, a dataset used in a global ﬁeld modeling has to fulﬁll the following

requirements:

• samples should be taken at evenly distributed points, dense enough to cover the

shortest wavelengths,

• readings at different locations should be taken simultaneously,

• measurements should be made in areas free of electric currents, i.e. free of

sources of induced magnetic ﬁelds.

These three conditions could be satisﬁed by a dense ground-based network.

In reality, as shown before, the observatory network is not dense enough and

rather unevenly distributed. This weakness can be overcome by satellite measure-

ments. Using only magnetic ﬁeld observations from space has, however, also its

short-comings. For example, the last two requirements can not be fulﬁlled by

a single satellite. Satellites take measurements sequentially orbit-by-orbit, and it

takes several days or even months to achieve an appropriate global coverage. In

order to compensate for this weakness temporal changes of the magnetic ﬁeld dur-

ing the considered interval have to be corrected or co-estimated. Since satellites

orbit the Earth in the ionosphere, they cross various kinds of currents. For the

mitigation of this problem two procedures are possible: one is to remove the mag-

netic effects of these currents from the recorded data, and the second is to select

time intervals when the currents, which cannot be corrected, are sufﬁciently weak

(see below).

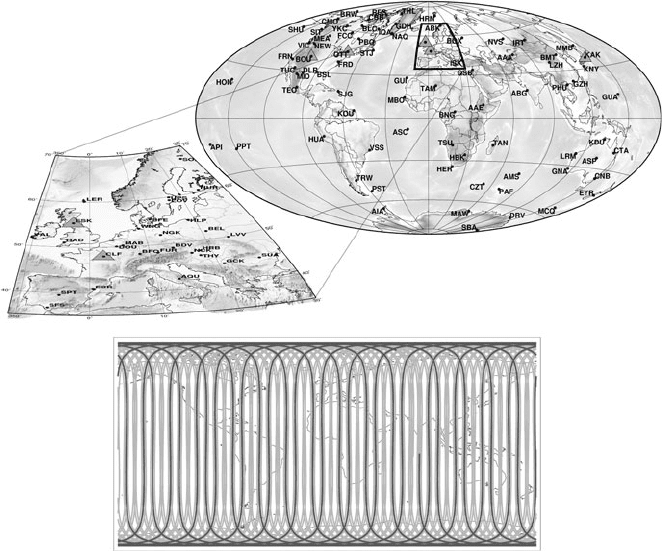
Spatial distribution. The distribution of magnetic observatories over the globe

(Fig. 13) is highly non-uniform. A possibility to counterbalance this uneven geo-

graphical distribution is the use of an adequate weighting scheme (Langlais and

Mandea, 2000). However, adequate weighting cannot make up for the lack of infor-

mation in the regions sparsely covered by data. Another possibility to improve our

knowledge of the secular variation is to have well-distributed global measurements

496 M. Mandea et al.

Fig. 13 Map of the INTERMAGNET magnetic observatory distribution (top). Coverage of the

Earth with CHAMP satellite magnetic data after 1 day DOY 288 2007 (black)and1week(DOY

226-232 2007) (grey, bottom)

from satellites. The data provided by each of the three satellites currently in orbit

ensure a good coverage of the Earth’s surface over a 4-month period. Figure 13

shows the orbit tracks for 1 day and for 1 week, respectively, for the CHAMP satel-

lite. The coverage over 1 week already appears sufﬁcient for a good data distribution

in space, but this coverage is not sufﬁcient in local time. Moreover, these plots are

based on all available measurements, without considering data quality and selection

criteria with respect to external disturbances.

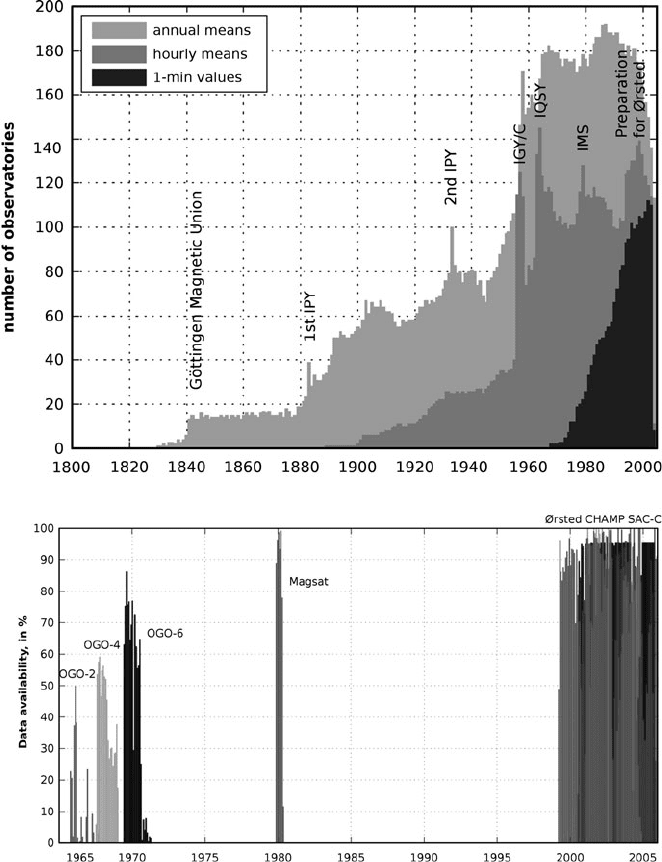
Temporal coverage. The number of observatories providing hourly means or

1-minute data (INTERMAGNET observatories) is lower than the total number of

worldwide observatories. Nevertheless, they cover a large time-span when compar-

ing with the satellite missions. Figure 14 indicates the time-span covered by the

number of observatories providing different data, and also the short interval covered

by satellite missions.

Magnetic ﬁeld measurements obtained by various platforms have their strengths

and weaknesses. By properly combining these data, information about the charac-

teristics of the geomagnetic ﬁeld can be retrieved. This is shown in the following

sections.

The Earth’s Magnetic Field 497

Fig. 14 Temporal distribution (in 2005) of the various kind of data provided by magnetic observa-

tories (top). Temporal distribution of the satellite missions carrying a scalar magnetometer (POGO

series) or a scalar and vector magnetometer (MAGSAT, Ørested, CHAMP, SAC-C)

3 Data and Field Modeling

An important prerequisite for deriving more precise and higher resolution models

of the geomagnetic ﬁeld is the availability of high-quality measurements. Under the

assumption of suitable data the modeling task may be separated in a few crucial

498 M. Mandea et al.

steps. The ﬁrst one is linked to data selection, as in each single measurement all

contributions exist, and the wish is to minimize the external ones. Thereafter, the

inversion of the measurements to obtain a mathematical description of the ﬁeld

distribution is at a global or regional scale.

Before presenting in some more details a description of the geomagnetic ﬁeld

produced by the lithosphere, we summarize the efforts needed in a good data

selection process, as well as the basis for the global and regional modeling.

3.1 Data Selection

3.1.1 Data Selection – General Needs

Before applying different techniques to available measurements, a selection of dif-

ferent datasets is needed. This process is generally different from one modeler to

another, however, the main idea is to minimize as much as possible the various exter-

nal contributions. For example, the GRIMM model

(Lesur et al., 2008), mainly

used in the following in magnetic ﬁeld description, is built using exclusively vector

magnetic data. The main motivation for this choice is the need to use satellite mea-

surements during polar summers. Therefore, the ﬁelds generated by ﬁeld aligned

currents and in the ionosphere have to be modeled at high latitudes, and this can be

achieved only if vector data are available at all local times.

GRIMM model covers the time span 2001–2005, when CHAMP vector data with

acceptable quality ﬂag settings are available. Using two magnetic components only

lead to a robust model and it has the further advantage that there is no need to

model the ﬁeld generated by the ring current. The CHAMP measurements have

been selected between ± 55

◦

magnetic latitudes such that

• IMF B

has positive values

• 20 s minimum separate two data points

• the local time (LT) is in between 23:00 and 05:00

• the sun is below the horizon up to 100 km above the Earth’s reference radius

• the VMD (Thomson and Lesur, 2007) norm is no larger than 20 nT and the norm

of its derivative is less than 100 nT/day.

At magnetic latitudes outside the ± 55

◦

interval, the three components of the

magnetic data vector are used. CHAMP data with acceptable quality ﬂag settings

are selected for positive IMF B

values, with 20 s minimum between two data

points, a VMD norm no larger than 20 nT and the norm of its derivative is less

than 100 nT/day. The use of the full magnetic vector at all local times is necessary

for separating the ﬁeld generated by ﬁeld aligned currents or in the ionosphere from

the internal core ﬁeld. Using the full vector data at high latitude also improves the

www.gfz-potsdam.de/magmodels/GRIMM

The Earth’s Magnetic Field 499

robustness of the low order internal Gauss coefﬁcients, in the same way that vector

data are used at mid-latitudes to avoid the Backus effect in models built mainly from

scalar magnetic data.

GRIMM model is also based on observatory hourly mean values, selected

following the same criteria, as for the between ± 55

◦

magnetic latitudes.

3.1.2 Data Selection – New Approach

The new satellite era brings us in a situation when a large number of mag-

netic measurements has became available, due to the three magnetic missions,

Ørsted, CHAMP and SAC-C. The forthcoming ESA’s Swarm constellation mission,

scheduled for launch in 2011, will dramatically increase this number.

In this context, modeling t he magnetic potential ﬁeld of the Earth becomes a chal-

lenging task with high demands on computer memory and time. As noted before,

for internal ﬁeld modeling, the measurements are selected according to the quiet

geomagnetic conditions (geomagnetic indices, local time, etc). Nevertheless, the

number of data remains important. Often, the number of measurements, taken into

account in inversions, is simply reduced by decimating them. Such a “random selec-

tion” may obviously lead to loss of information. In addition, not only the satellite

data, but also surface data have been considered. High resolution ﬁeld modeling,

at global or regional scales, indeed requires to combine the “medium” resolution

satellite measurements with very dense surface datasets comprising ground-based,

airborne and marine measurements. This increases considerably the size of the

datasets from which the potential ﬁeld models are computed.

To overcome these possible drawbacks, it appears necessary to develop tech-

niques to deal with these large amounts of data. Recently, two important aspects

have been considered: ﬁrstly, the data have to be preprocessed in a compact and

reasonable way, secondly, the design of the model and the inversion scheme have

to allow fast and local computations. Thus, Minchev et al. (2009) have proposed

to take advantage of: (i) the rather smooth behavior of the internal magnetic ﬁeld at

satellite altitude and (ii) the mathematical and geometrical properties of the wavelets

frames (see below), which can be used as a modeling technique. In this context, local

multipole approximations of the wavelets at satellite altitude, have been developed.

To cope with the large number of satellite measurements, and in particular with

some 300 millions of measurements, from the upcoming 4-year Swarm multisatel-

lite mission, methods have been developed to avoid the storage of large normal

matrices needed for a large number of spherical harmonics. Those methods are

based on the iterative approach (see for instance Kusche, 2000; Schuh, 2000; Keller,

2001). They make use of a matrix that is representative of the normal system, but

easier to compute. Such matrix allows to compute an approximate solution of the

normal system, that is iteratively reﬁned. It can also be used as a pre-conditioner of

the normal system, allowing to speed-up convergence rates of iterative solvers.

In Minchev et al. (2009) the space-domain is decomposed, i.e. a shell at satellite

altitude is deﬁned by the measurement positions, into a sum of geometrical 3D-

bodies (triangular prisms). Each unity-volume contains a certain amount of ﬁeld

500 M. Mandea et al.

measurement points. As soon as the considered unity-volume is small enough, the

data are located in the vicinity of each other and the ﬁeld itself appears smooth. In

the inverse problem, the expansion of the related magnetic ﬁeld in wavelets frames

may be replaced by a power series of local multipole developments around the centre

of mass of the data positions inside the deﬁned volume. In this way, a piecewise

decomposition of the magnetic ﬁeld is obtained, at satellite altitude. The coefﬁcients

of each local development may then be used in global ﬁeld modeling. Let us describe

in more detail the space discretization at the satellite level.

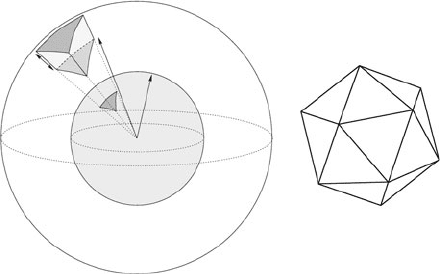
The space, where the satellites revolve, is considered as a shell. Its thickness is

directly deﬁned by the range of radius of the considered data positions according to

geocentric coordinate system. This shell is discretize to K number of unity-volumes

(with j=1,...,K) equivalent to the number of facets of an icosahedron centered

onto the Earth (Chambodut et al., 2005).

Each unity-volume P

is deﬁned such that it gets property of compact geometry:

its thickness is chosen to be more or less equivalent to the size of the icosahedron

edges at the satellite altitude. If the thickness of the shell deﬁned by the data is large,

another layer of unity volume is added in the radial direction. The aim is to obtain

unity-volumes with reasonable shapes, neither ﬂat thin shells, nor long thin radial

columns, as shown in Fig. 15.

For a given dataset, the balance should be determined between the number

of unity-volume K (directly related to their size), the number of data per unity-

volume M

(with j=1,...,K) and the degree of multipole expansion inside a prism

(Chambodut et al., 2005). For example, in case of a few data in a large unity-volume,

this conﬁguration may allow recovery of large wavelengths potential ﬁeld, and thus

leads to the use of low degree polynomials. At the contrary, in case of a large number

of data in a small unity-volume, this conﬁguration may allow recovery of smaller

wavelengths potential ﬁeld, and thus leads to the use of higher degree polynomials.

A crucial question regarding the use of the multi-polar expansion technique

arises. Depending on the size of the considered dataset, how the size of the

Fig. 15 A unity-volume at satellite altitude (left); the simplest icosahedron – 20 faces (right)

The Earth’s Magnetic Field 501

unity-volumes (the number of data per unity-volume) and the maximal order of

the local harmonic polynomials have to be chosen. This choice has to be done

to obtain optimal performances. It is clear that the higher the resolution of the

space discretization is, the better the approximation will be. On the other hand,

the maximal reduction of the size of the underlying problem, is obtained for the

lowest possible resolution. Therefore, it is needed to ﬁnd a balance between the

resolution of the space discretization and the degree of the local expansion used in

the model.

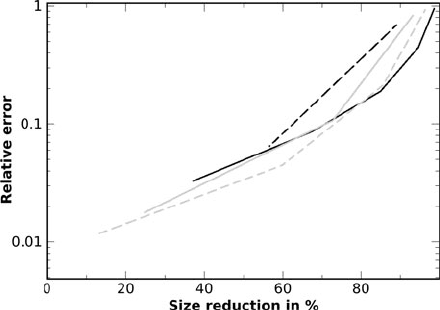
Figure 16, shows the maximum relative error between all spherical harmonics up

to degree 30 and their corresponding local multi-polar approximations, versus the

ratio (in %) between the sizes of the underlying and the approximated problems (size

reduction), for a given dataset. For small and moderate size datasets, low orders local

approximations, of ﬁrst (L = 4) and second (L = 9) orders, are preferable. Higher

order approximations would be beneﬁcial, when a dataset is large enough, so the

number of local coefﬁcients per unity-volume can be compensated by the amount

of data approximated in each cell.

In Minchev et al. (2009) two cases have been investigated, for the gravity and

magnetic ﬁeld. It has been shown that depending on the chosen precision of the

approximation, the speed and the quality of the inversion can practically be con-

trolled. Thus, fast quick-look solutions or highly precise models can be computed

with a great deal of ﬂexibility. The performed tests have also shown that the amount

of errors introduced by approximations in models can be controlled. Distortions are

small, and become negligible when the process is iterated. This new method can

be applied to any kind of modeling functions like wavelets or other radial basis

functions.

Fig. 16 Ratio in % between the sizes of the original and the approximated problems versus the

approximation relative error for L = 4(black), L = 9(dashed grey), L = 16 (grey), L = 25 (dashed

black)

502 M. Mandea et al.

3.2 Global Modeling

The most commonly employed global method to represent the geomagnetic ﬁeld

is the Spherical Harmonic Analysis (SHA). In a space deﬁned by three spherical

coordinates (r, θ, φ), the geomagnetic induction ﬁeld B can be expressed as

B =−∇V (13)

where V is a scalar potential satisfying V=0.

At the Earth’s surface this potential can be expressed as the sum:

V = V

+ V

(14)

where V

and V

represent the internal and external scalar potential, respectively.

In spherical coordinates equation V=0 can be written as

∂

∂r



∂V

∂r



sin θ

∂

∂θ



sin θ

∂V

∂θ



sin

∂

∂φ

− 0 (15)

and it is solved by separation of variables and then expanded into a s pherical

harmonic series (see below).

Harmonics are widely used in mathematics and physics to represent complex,

usually natural, functions. These harmonics are periodic functions of varying ampli-

tude and period. The more harmonics are used, the closer the approximation to

reality is.

In the absence of magnetic sources, the geomagnetic ﬁeld can be presented as

the negative gradient of a potential: B

= –V(θ ,φ,ρ,τ ). The source of this poloidal

ﬁeld can be from internal or from external origin and the associated potentials, V

and V

respectively, are described on a spherical surface. Following (Gauss, 1839),

the two potentials V

and V

can be developed as spherical harmonic expansions:

(θ, φ,r,t) − a



l,m





l+1

(t)Y

(θ, φ) (16)

(θ, φ,r,t) − a



l,m





(t)Y

(θ, φ) (17)

where θ and φ are the colatitude and longitude, a =6,371.2 km is a reference radius,

(θ,φ) are the usual Schmidt normalized spherical harmonic (SH) functions and

(t), q

(t) are the Gauss coefﬁcients. The convention used here is t hat negative

orders (m < 0) are associated with sin(mφ) terms, whereas zero or positive orders

(m ≥ 0) are associated with cos(mφ).

Traditionally, the North, East, Vertical down system of coordinates is used to give

the expression of the gradient of the potential. Here, as for the GRIMM model, the

geocentric Cartesian system of coordinates is used. The direction Z of the geocentric

Cartesian system of coordinates (i.e. ≈ the Earth’s rotation axis) is considered, ﬁrst.

Also, it is assumed that an optimal distribution of vector data at satellite altitude

The Earth’s Magnetic Field 503

is available, such that a magnetic ﬁeld model can be robustly built. The data set is

made of the Z component of the measured magnetic ﬁeld. The magnetic ﬁeld of

external origin in this Z direction is given by:

=−cos θ · ∂

(θ, φ,r,t) + sin θ ·

∂

(θ, φ,r,t) (18)

which leads to:

=−



l=1



m=−1





l−1

(t)

(l +|m|)(l −|m|)Y

l−1

(θ, φ) (19)

The external ﬁeld is generally assumed to be large scale and generated mainly

in the magnetosphere which justify the use of L = 2 as the maximum SH degree.

Considering only the ﬁrst degree (l = 1), only the order m = 0 appears and therefore

only the SH function Y

(cos θ) is involved. This function is a constant in space, so,

as expected, the large scale external ﬁeld along the Z direction (i.e. associated with

) is a constant in space. The ﬁeld of internal origin is given by:

=−



l=1



m=−1





l+2

(t)

(l +|m|+1)(l −|m|+1)Y

l+1

(θ, φ) (20)

In this equation for a given degree l the SH function is Y

l+1

(θ, φ) whereas it was

l–1

(θ, φ) in the expression 19 of the external ﬁeld. If the maximum SH degree

L = 2 is and acceptable approximation for the external ﬁeld, the SH function of

the highest degree in equation 19 is Y

(θ) whereas in Eq. (20) the SH function of

the minimum degree is Y

(θ, φ). Therefore using only the distribution of Z data

described above leads to a separation of the internal and external ﬁeld contributions

to the magnetic ﬁeld. It leads also to a unique set of Gauss coefﬁcients. However,

for a better accuracy one of the two other directions can be used. The expressions

for the internal poloidal ﬁeld in the X and Y directions are:

=−



l=1





l+2

√

(l +1)(l + 2)g

(t)Y

l+1

(θ, φ)



m=1

√

(l +m + 1)(l + m + 2)(g

(t)Y

m+1

l+1

(θ, φ) + g

−m

(t)Y

−m−1

l+1

(θ, φ))

−



m=1

√

(l −m + 1)(l − m + 2)(g

(t)Y

m−1

l+1

(θ, φ) + g

−m

(t)Y

−m+1

l+1

(θ, φ))

(

(21)

=−



l=1





l+2

)

√

(l +1)(l + 2)g

(t)Y

−1

l+1

(θ, φ)



m=1

√

(l +m + 1)(l + m + 2)(g

(t)Y

−m−1

l+1

(θ, φ) + g

−m

(t)Y

m+1

l+1

(θ, φ))

−



m=1

√

(l −m + 1)(l − m + 2)(g

(t)Y

−m+1

l+1

(θ, φ) + g

−m

(t)Y

m+1

l+1

(θ, φ))

(

(22)

Over the polar regions, the vector satellite data are strongly contaminated by the

ﬁeld generated by ﬁeld aligned currents (FAC). At satellite altitude part of this ﬁeld

is toroidal and is given by: B

= –η ×∇

(θ,φ,t) where η is the unit vector in the