Fishwick P.A. (editor) Handbook of Dynamic System Modeling

Подождите немного. Документ загружается.

14-12 Handbook of Dynamic System Modeling

Ports

Other polygons: different model types

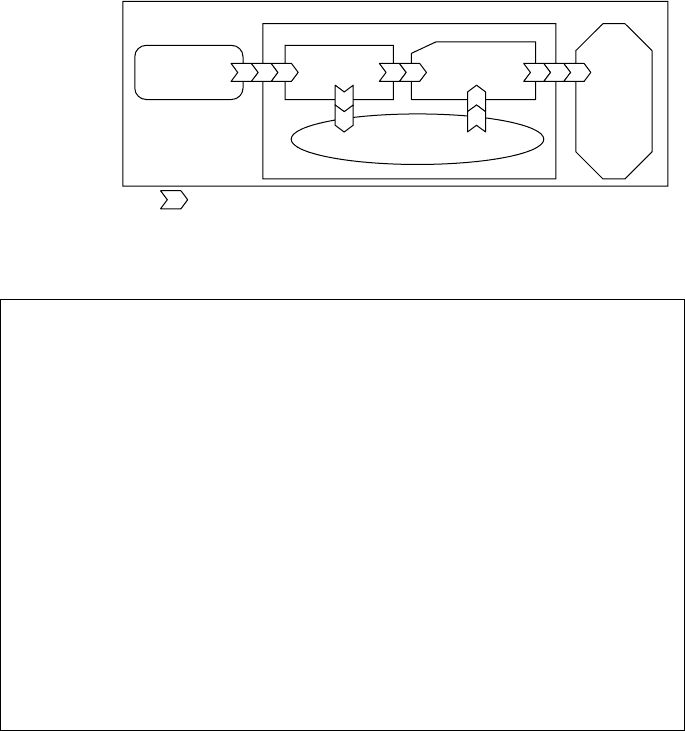
FIGURE 14.10 MXL multimodel structure.

<?xml version="1.0" encoding="utf-8"?>

<MXL>

</block>

</block>

</fbm>

</MXL>

FIGURE 14.11 Functional block model in MXL.

14.3.2 Multimodeling in MXL

Suppose a system could be represented as multimodeling concepts. The system has an FBM with two

blocks (i.e., functions) and one trace; the second block contains an FSM with two states and two transitions

(i.e., interlevel coupling). Figure 14.11 and Figure 14.12 show the MXL representation for the system.

In Figure 14.11, the MXL contains fbm and simulation as subelements. fbm represents model type

(i.e., FBM) and has two elements, block and trace. Each block element has an attribute, id, to specify the

names of blocks. In addition, the element has port information, input or output as well as its function-

ality, script.Eachinput and output element contains id, datatype, and index, which deﬁne the name of

input/output, data type of input/output, and the number of input/output, respectively. The script element

has lang, src, and func to specify program language, the name of the script ﬁle, and function to be exe-

cuted, respectively. If a block contains another model type (i.e., multimodel), the model type and its MXL

can be speciﬁed in the block (i.e., Block F2 in Figure 14.11.) trace has from and to attributes denoting

connectivity between blocks. Simulation has speciﬁc information for executing a certain dynamic model

such as start time, end time, and delta time. Figure 14.12 depicts an internal dynamic model type which

Block F2 contains. In this case, the MXL represents the FSM. Therefore, MXL has state and transition as

subelements. Likewise, each state and transition has its id, script information, and topological connectivity.

Multimodeling 14-13

<?xml version="1.0" encoding="utf-8"?>

<MXL>

</state>

</state>

</transition>

</transition from="S2" to="S1">

</fsm>

</MXL>

FIGURE 14.12 Finite state model in MXL.

Using an MXL-to-DXL translator, the MXL ﬁle can be translated into DXL, which is a homogeneous

assembly level block diagram modeling language consisting of Connectors, Blocks, and Ports. The concepts

of DXL will be explained semantically and syntactically in the next section.

14.4 Dynamic Exchange Language (DXL)

14.4.1 DXL Concepts

DXL is a uniﬁed, low-level functional speciﬁcation language, and associated diagrammatic presentation

for simulation on the RUBE framework. In simple DXL models, models are deﬁned by connection of

input and output ports of primitive models such as multipliers or adders.

In DXL multimodels, the models may be abstracted upper-layer block models in the form of sublayer

models. DXL combines the lower-level block models of subsystems to describe a complex system hierarchi-

cally (i.e., homogeneous multimodeling). Because each DXL model has its outermost block as a wrapper,

it supports the important characteristics for multimodeling, composability, and reusability.

When each block plays a role as a leaf node in the structure of a multimodel, it can be encoded in one

of the programming languages, such as JavaScript or Python. Multiple programming languages become

the target codes for DXL-to-simulation translators, and an actual data ﬂow for simulation is achieved by

using XML data and schema.

In this section, a diagrammatic presentation and formalism for DXL, which operates like a circuit, is

created. Ports constitute the interface that deﬁnes the boundary of components or subsystems in a system

conﬁguration. MXL and DXL ports are used for port coupling where all ports match in number and data

type. MXL ports are used for conceptual multimodeling in the RUBE framework. DXL ports, however, are

utilized to support the multimodel execution as well as to maintain the conceptual multimodeling. A DXL

or MXL model supports not only streaming of simple data types but also XML “information streaming”

since DXL ports are capable of encoding documents (i.e., XML documents) rather than data under the

XML-based environment. XML schemata that deﬁne the typing structure accompany the “types.”

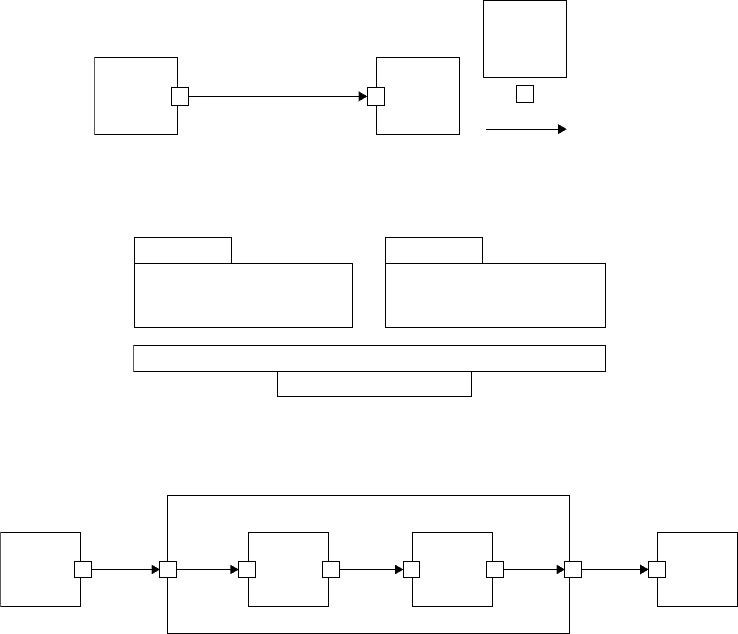
14-14 Handbook of Dynamic System Modeling

14.4.2 Syntax of DXL

The right side of Figure 14.13 shows syntax elements of DXL. DXL elements are composed of blocks, input

and output ports, and connects. Generally, a DXL model is composed of “block” and “connect” elements.

A DXL block element is composed of “port” elements and “its actual computation codes.” DXL block

elements are connected by each connect element through input and output port elements, which can be

included in a block element. Each port element is connected to the corresponding output and input port

elements of other block elements for its data ﬂow, which each connect element controls.

The left side of Figure 14.13 shows a simple DXL model consisting of two blocks and one connect. This

model shows that the output becomes the input of “Block 2” after the computation of “Block 1”is ﬁnished.

Therefore,“Block 2” executes its own computation using the output of “Block 1” as its input.

Each block becomes an object in object-oriented programming unlike a function in procedure program-

ming. Input and output ports become the variables that are deﬁned in the block objects according to their

data types such as primitive and object data types. From the viewpoint of object-oriented programming,

therefore, the DXL model of Figure 14.13 is explained in Figure 14.14.

The DXL block element might include another DXL model when it represents a homogeneous multi-

model. In Figure 14.15,“Outer Block B” does not have “its actual computation codes,” but it does contain

another DXL model. Therefore, when “Outer Block B” starts, the input of “Outer Block B” becomes the

input of “Inner Block a.” In contrast, when “Outer Block B”ﬁnishes, the output of “Inner Block b”becomes

the output of “Outer Block B.”According to the ﬂow of “connect”elements, after the inner blocks of “Outer

Block B” are executed, the output of “Outer Block B” becomes the input of “Block C” in Figure 14.15.

Input

port

Output

port

Port

Block

Connect

Block 1 Block 2

FIGURE 14.13 DXL syntax.

Object B1

Input ports variables

Output ports variables

Methods

Object B2

Input ports variables

Output ports variables

Methods

When the output of B1 is sent to the input of B2

B2.input = B1.output

FIGURE 14.14 DXL programming semantics.

A. OP

Inner Block a

Block A

Inner Block b

Outer Block B

B. IP B. OPa. IP b. IP

a. OP b. OP

Block C

C. IP

FIGURE 14.15 DXL multimodel syntax.

Multimodeling 14-15

14.4.3 Semantics of DXL

14.4.3.1 Notation

Figure 14.16 deﬁnes a notation to describe the functionalities of DXL blocks. We describe algorithmic

semantics of blocks using a set theory and some pseudocodes. IP and OP mean input port and output

port of a block. For notation of DXL ports, the orders of the ports are expressed as an argument of IP or

OP, and the identiﬁers of their parent blocks are subscripted. Therefore, the ﬁrst and second input ports

ofblockB1becomeIP

(1) and IP

(2). The ﬁrst and second output ports of block B1 become OP

(1)

and OP

(2). OB means output blocks of current block. The input ports of these output blocks receive

the output after the current block ﬁnishes its computation. For notation of DXL output blocks, the orders

of output ports of the current block are presented as arguments of OB, and the identiﬁer of the current

block is subscripted. Therefore, the output blocks of the ﬁrst and second output ports of the current block

B1 become OB

(1) and OB

(2).

14.4.3.2 Information Stream Mechanism

Generally, a DXL model is composed of “block”and“connect”elements. A DXL block element is composed

of“port”and“deﬁnition”elements. It mightinclude another DXL model when it represents a homogeneous

multimodel. The DXL block elements are connected by each connect element through the input and

output port elements, which are included in a block element. The data ﬂow between block elements is

notated by the pseudocode SEND, which means different information streaming according to the various

environment modes. For example, the pseudocode SEND means “generate next event” based on discrete-

event scheduling methods (Fishwick, 1995) in sequential simulation, and also “send message” based on

message-passing protocols in distributed simulation. This information streaming abstraction approach,

which is used to generate different target codes on heterogeneous environments, makes it easy to create a

DXL-to-simulation translator and integrate model components.

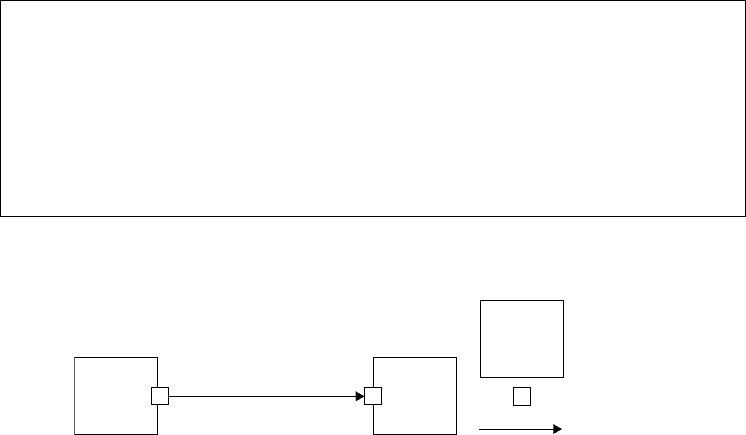
In Figure 14.17, the meaning of the SEND pseudocode is “transfer DATA in an output port OP of a block

B1 to an input port IP of a block B2 and generate next event B2, after time t passes,”based on discrete-event

scheduling methods. If this model is based on message-passing protocols in distributed simulation, this

Notation

: a set of input ports for a block i

(n): the nth input port of a block i

: a set of output ports for a block i

(n): the nth output port of a block i

(j): a set of output blocks for the jth port of a block i

SEND(t, DATA(i), IP

(j)): Current block sends data of ith output

port to jth input port of block k after time t

FIGURE 14.16 DXL block notation.

(1)OP

(1)

SEND (t

, DATA(1), IP

(1))

Input port

Block

Connect

Block 1 Block 2

FIGURE 14.17 Augmented DXL syntax.

14-16 Handbook of Dynamic System Modeling

(1)

(m) OP

(n)

(1)

SEND (t

, DATA(1), IP

(1)) SEND (t

, DATA(1), IP

(1))

SEND (t

, DATA(1), IP

(m)) SEND (t

, DATA(1), IP

(1))

Block 1

Block m

Block 1

Block n

Block i

(1)

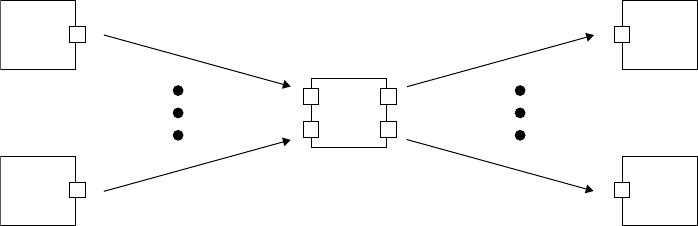
FIGURE 14.18 Examples of SEND pseudocode.

SEND pseudocode means “create DATA in an output port OP of a block B1 as a message and send the

message to an input port IP of a block B2, after time t passes.”

In Figure 14.18, the meanings based on discrete-event scheduling methods of SEND pseudocodes are

as follows:

•

SEND (t

, DATA(1), IP

(1)): transfer DATA in an output port OP of a block B

to an

input port IP1 of a block B

and generate next event B

, after time t

passes.

•

SEND (t

, DATA(1), IP

(m)): transfer DATA in an output port OP of a block B

to an

input port IPm of a block B

and generate next event B

, after time t

passes.

•

SEND (t

, DATA(1), IP

(1)): transfer DATA in an output port OP1 of a block B

to an

input port IP of a block B

and generate next event B

, after time t

passes.

•

SEND (t

, DATA(1), IP

(1)): transfer DATA in an output port OPn of a block B

to an

input port IP of a block B

and generate next event B

, after time t

passes.

In Figure 14.18, the meanings based on message-passing protocols in distributed simulation of SEND

pseudocodes are as follows:

•

SEND (t

, DATA(1), IP

(1)): create DATA in an output port OP

of a block B

as a

message and send the message to an input port IP

of a block B

, after time t

passes.

•

SEND (t

, DATA(1), IP

(m)): create DATA in an output port OP

of a block B

as a

message and send the message to an input port IP

of a block B

, after time t

passes.

•

SEND (t

, DATA(1), IP

(1)): create DATA in an output port OP

of a block B

as a

message and send the message to an input port IP

of a block B

, after time t

passes.

•

SEND (t

, DATA(1), IP

(1)): create DATA in an output port OP

of a block B

as a

message and send the message to an input port IP

of a block B

, after time t

passes.

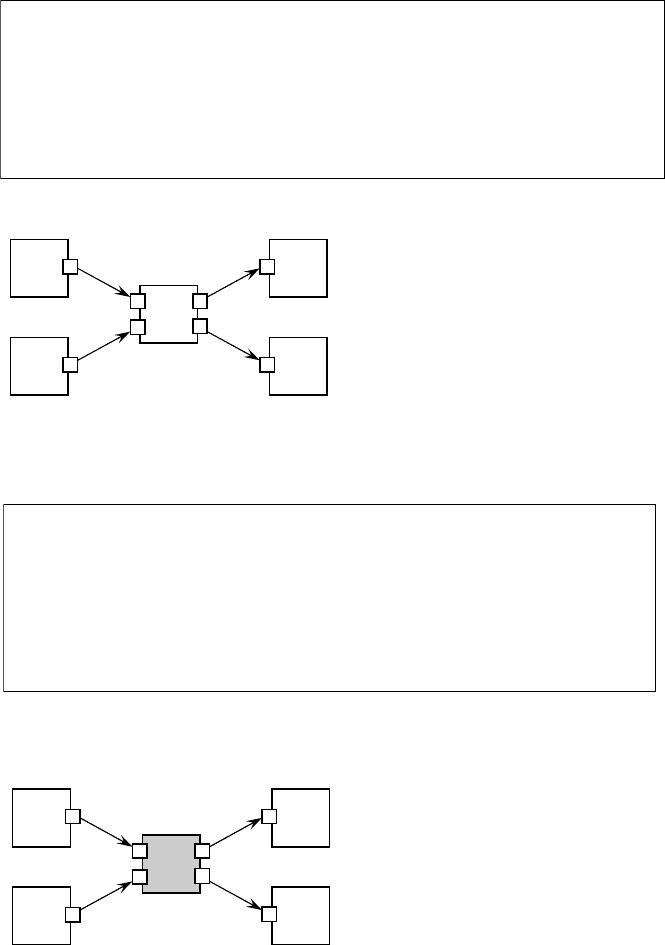
14.4.3.3 Synchronous Input Property

Block B3 in Figure 14.19 divides the output of block B1 with the output of block B2 and then sends its

quotient to block B4 and remainder to block B5. To make the division, block B3 should have two inputs at

the same time (i.e., a synchronous block in DXL). Note that the block has two output ports to support a

different output at the same time unlike the functions of traditional programming languages, which have

only one output. The right side of Figure 14.19 describes the processing algorithm of block B3.

14.4.3.4 Asynchronous Input Property

In Figure 14.20, block B3 plays a role in switching input data. It is not necessary to receive both inputs to

relay its data. In other words, the block just relays its input to its next block whenever it receives the input.

The block should therefore have an asynchronous input property, which is depicted with a gray color. The

switch block algorithm is described on the right side of Figure 14.20. In DXL, the above combinations of

simple blocks and their properties create an actual model for a system.

Multimodeling 14-17

Algorithm for a block having synchronous inputs

if(for ∀x∈IP

, x has input data) then

The computation of the function in a DXL block

For ∀y

∈P

, if(y has output data) then for z∈OB

(y), SEND(t,

DATA(y), z) elseif

IP1

IP2

OP1

OP2

Algorithm for block B3

if (for ∀x

∈IP

, x has input data)

then

(1) ← IP

(1)/IP

(2)

(2) ← IP

(1)%IP

(2)

SEND(t

, DATA(OP

(1)), B4)

SEND(t

, DATA(OP

(2)), B5)

elseif

(ⴜ)

FIGURE 14.19 Example of synchronous inputs.

Algorithm for a block having asynchronous inputs

if(for ∃x

∈IPi, x has input data) then

The computation of the function in a DXL block

For ∃y

∈OP

, if(y has output data) then for z∈OB

(y),SEND(t,

DATA(y), z) elseif

Algorithm for block B3

if (IP

(1) has input data) then

(2) ← IP

(1)

SEND(t

, DATA(OP

(2)), B5)

elseif

if (IP

(2) has input data) then

(1) ← IP

(2)

SEND(t

, DATA(OP

(1)), B4)

elseif

IP1

IP2

OP1

OP2

switch

FIGURE 14.20 Example of asynchronous inputs.

14.4.4 Multimodeling

ForDXL,multimodeling is deﬁned by specifyinga block circuit inside of a block, and continuingrecursively

as needed. Ports are coupled by ensuring matching data types for each connecting port on each connector.

The general DXL methodology in transforming heterogeneous models (MXL models) into homogeneous

models (DXL models) is as follows:

•

Transform submodels in an MXL multimodel into DXL models and

•

Incorporate each of the transformed models according to port coupling.

14-18 Handbook of Dynamic System Modeling

Translation

x

x x

a

兰兰



兰兰



FIGURE 14.21 Translation of an FBM into a DXL model.

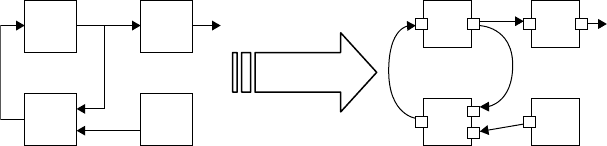
14.4.4.1 FBM-to-DXL Translation

The FBM is composed of functional elements where functions, along with inputs and outputs, are often

depicted in a “block” form. An arbitrary number of blocks can be coupled to form an FBM. This FBM is

similar to DXL except for synchronous and asynchronous inputs of DXL. Therefore, functions of FBM

are translated into DXL blocks, and FBM’s inputs and outputs are translated into DXL input and output

ports. Because each block of traditional FBM has a pure function, all inputs of the function should be

valid before the block is executed, meaning all FBM blocks have synchronous property for inputs.

An FBM for the differential equation x



=−ax



is described on the left side of Figure 14.21. This

FBM is composed of four blocks: two integrators, one multiplier, and one constant. Because each block

of a traditional FBM has a synchronous input property, these blocks are translated into blocks having

synchronous inputs in DXL. Its arrows are translated into connectors of DXL. This FBM also has a

continuous simulation property. To support the property, a start block of the DXL model is generated

every simulation unit time.

14.4.4.2 FSM-to-DXL Translation

The FSM has states and transitions. A state represents the current condition or “snapshot” of a system

for some length of time. Transitions enable the system to move from one state to another during the

simulation while under the control of the system input. The basic rule of translating FSM into DXL is that

all functional elements are translated into DXL blocks. The transitions of FSM are predicates under the

system input and can, therefore, be translated into DXL blocks. These DXL blocks have the same type of

input ports as the system input and a Boolean type of output ports that decide whether the predicates are

true or false. Since states have the functional properties to access the system input, all states are translated

into DXL blocks. In addition, we need the special block to control the system input.

The left side of Figure 14.22 shows an FSM modeling of a four-stroke gasoline engine with four phases:

compression, ignition, expansion, and exhaustion. The key point that makes FSM different from FBM is a

state-based model. To translate a state-based model into a function-based model, all states and transitions

are translated into DXL blocks. Then DXL connectors and block properties control the semantics of

the state-based model. The right side of Figure 14.22 shows a translated DXL model for the four-stroke

gasoline engine. If we made a DXL code manually, we could create a simpler DXL code than the right side

of Figure 14.22. But to make automatic MXL-to-DXL translation easy, we used the DXL model to include

INPUT and OUTPUT blocks, as in Figure 14.22. Our translator generated the INPUT and OUTPUT

blocks to control the FSM semantics. The right blocks next to INPUT blocks are translated transition

blocks and the right blocks next to OUTPUT blocks are translated state blocks.

14.4.4.3 Multimodeling between Homogeneous Models

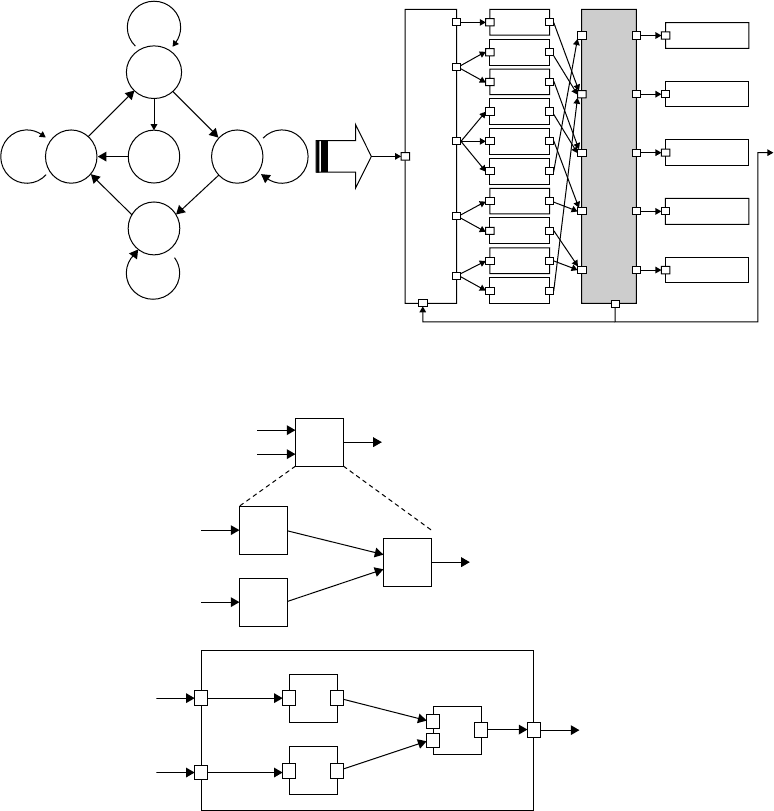
In Figure 14.23, the upper model is a two-level functional hierarchy, where function f is deﬁned in terms

of a composition of three other functions f

, f

, and f

. The lower model shows multimodeling in DXL

for the upper model. Because DXL is speciﬁcally based on a functional block diagram, FBM models in

Figure 14.23 are reﬁned only if the number and types of ports are matched.

Multimodeling 14-19

Ignition

Input

data

INPUT

OUTPUT

Off

O_C

C_C

C_I

I_I

I_E

I_O

E_E

E_Ex

Ex_Ex

Ex_C

Off

Expan-

sion

Expansion

Exhaus-

tion

Exhaustion

Compres-

sion

Compression

FIGURE 14.22 Translation of an FSM into a DXL model.

o  f(i

, i

)

o  f

), f

( i

))

o  f(i

, i

)

o f

), f

))

FIGURE 14.23 Multimodeling between functional block models in DXL.

In Figure 14.24, the upper model is a two-level ﬁnite state hierarchy, where state s

is deﬁned in terms of

another FSM. The lower model shows the transformed DXL model for the two-level ﬁnite state hierarchy.

All FSMs should have this kind of functional box around them to represent external input and output

semantics even though the functional box is not expressed explicitly in the FSM graphical representation.

Because FSMs represent behavior or dynamics of another component in multimodeling, an FSM is

inserted in it to represent a state more speciﬁcally. In that case, multimodeling between FSMs should be

supported, but there is a difﬁculty in integrating the two FSMs because of the implicit expression of input

and output in FSMs.

However, in DXL, states and transitions in FSMs are transformed into the same blocks. MXL-to-DXL

translator generates special blocks, which control state and transition blocks (i.e., INPUT and OUTPUT

blocks). In Figure 14.24, after a submodel (i.e., the lower FSM model) is transformed into a DXL model, it

is inserted in its upper state block and then connected with external input and output ports using connect

elements in DXL.

14-20 Handbook of Dynamic System Modeling

(i )

FIGURE 14.24 Multimodeling between FSM models in DXL.

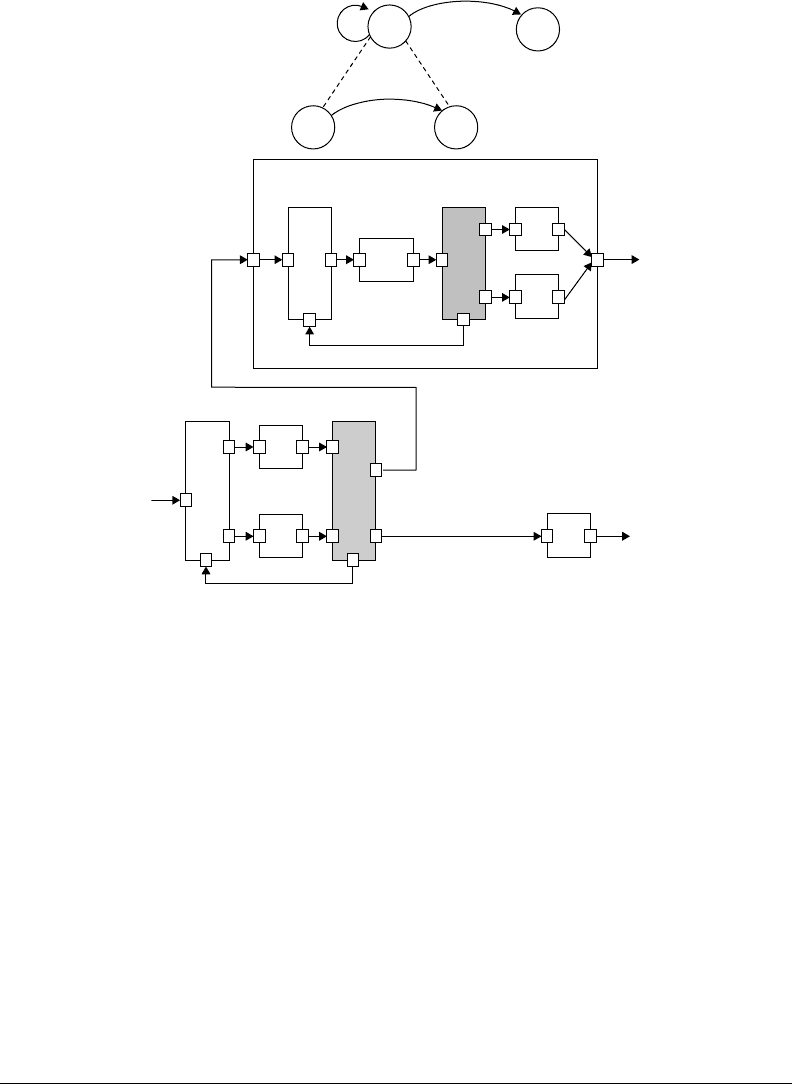
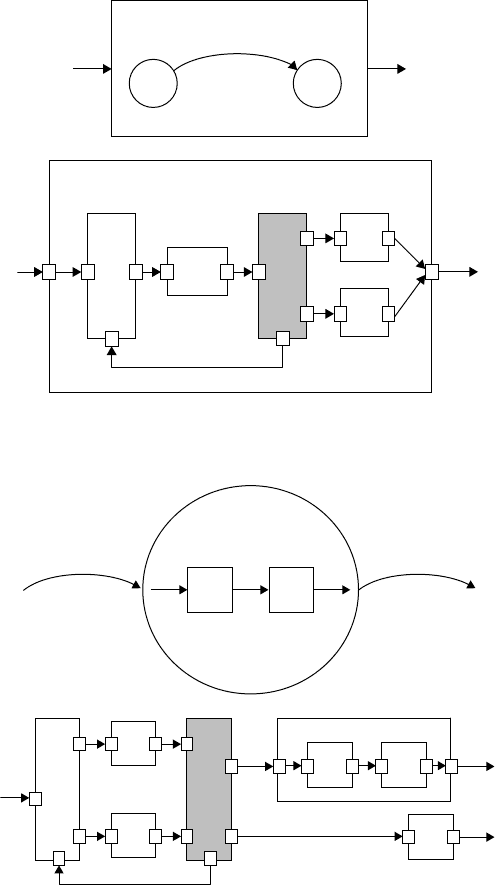
14.4.4.4 Multimodeling between Heterogeneous Models in DXL

In Figure 14.25, the upper model is the same model as shown in Figure 14.4. The submodel in this ﬁgure

is an FSM that deﬁnes the internal state transitions associated with function f . The generated DXL model

for an FSM is inserted in function f . Because the number and types of input and output of the function

f are the same as the input and output ports of the DXL model, the integration is accomplished through

port matching.

In Figure 14.26, a state of an FSM decomposes into an FBM to represent internal functionality. The

state in an FSM is different from an FBM from the viewpoint of a system. In an FSM, while input and

output are not speciﬁed explicitly, control ﬂow is unclear in an FBM. In a DXL model, however, the input

and output of transformed FSM states are speciﬁed explicitly, which makes it easier for the integration of

the components of an FSM and the components of an FBM. The lower model in Figure 14.26 indicates

a transformed DXL multimodel. A sublayer of the model, a transformed DXL model for an FBM, is

connected to the input and output ports of the outer state block s

14.5 A Boiling Water Example

In this section, we explain how multimodeling environments (i.e., integrative and general multimodeling

environments) can be implemented in the Blender 3D environment through our methodology, as proposed

in the previous sections, using the example of the boiling water scene. The pot is ﬁlled to a predetermined

level with water. A small amount of detergent is added to simulate the foaming activity that occurs

Multimodeling 14-21

p(i )

FIGURE 14.25 Multimodeling for an FBM including an FSM in DXL.

(i )

FIGURE 14.26 Multimodeling for an FSM including an FBM in DXL.

naturally when boiling certain foods. This system has a temperature knob. The knob is considered to be in

one of two states: on or off. We ﬁrst deﬁne the following conditions and assumptions in connection with

this scene:

•

External event: I ={ON, OFF}

•

Internal event: T ={T =α, α<T < 100, T =100}

•

Input space: {(I =ON, T =α), (I =ON, α<T < 100), (I =ON, T =100), (I =OFF, T =α),

(I =OFF, α<T < 100), (I =OFF, T =100)}

•

Boiling state: T =100

•

Heating state: T



(100 −T)

•

Cooling state: T



(α −T).