Fishwick P.A. (editor) Handbook of Dynamic System Modeling

Подождите немного. Документ загружается.

13-4 Handbook of Dynamic System Modeling

This is the ﬁnal result we are looking for. Of course, this is identical to the standard truss stiffness matrix

developed by traditional stiffness methods. However, the described shape function process can be extended

to other types of elements where the traditional stiffness-by-deﬁnition method is not possible.

13.1.2 Shape Functions

As seen in the previous section, one of the major variables in deriving a ﬁnite element is the choice of the

shape function H(x). Remember that it is the shape function that describes how the nodal displacements

are distributed throughout the element. In the truss member, it was assumed that the end displacements

are distributed linearly. This is an exact assumption for a uniform cross-section member.

The choice of the shape function is directly related to the number of unknowns in the element. The

number of unknowns deﬁnes the order of approximation that the shape function can have. Again for the

truss member, there were two unknowns (one at each end). This gave linear shape functions since two

points give a straight line.

As a result, to increase the accuracy of an analysis you need to increase the number of unknowns.

This can be handled by two methods: (1) you can increase the number of unknowns and use piecewise

continuous linear shape functions or (2) you can increase the number of unknowns and increase the order

of the shape function within an element. The next section will show the effects of these assumptions on a

simple example.

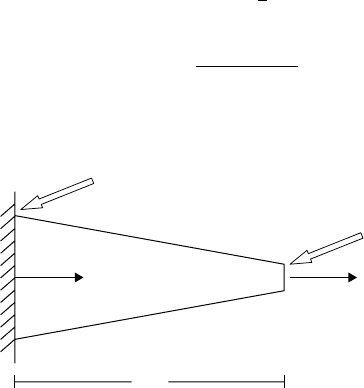
13.1.3 Tapered Extensional Example

For a constant cross-section truss member, there is no need to increase the accuracy above linear shape

functions. Instead, let us look at another simple problem. We want to see the effects of shape function

selection on accuracy when trying to solve a tapered member subjected to axial load for different modeling

conditions (see Figure 13.2).

The problem is simple enough that it can be solved exactly and the approximate ﬁnite element results

compared with this exact result. The problem has a unit thickness and is subjected to an axial load of 20.

Note that no units are given. Any consistent units are acceptable. The exact solution for the displacement

u(x) =−0.0074074 ∗ ln (10 −0.09 ∗x) +0.0170561

The solution was achieved by integrating the strain, ε =

. The exact solution for the stress, force over

area, in the section is

σ(x) =

10 −0.09 ∗x

(13.15)

We will use the FEM and solve the problem using three different assumed shape functions. First, we will

start by choosing a single unknown at the tip of the member. Second, we use two unknown displacements,

100

A(x)  10  0.09

xE  30,000

Unit thickness

(load)

Area  1

Area  10

FIGURE 13.2 Axial loaded tapered problem.

Finite Elements 13-5

one at the tip and the other at the midpoint. Using the two unknowns we have a choice, we can use a

quadratic shape function or we can use two linear functions. We will perform the analysis using both.

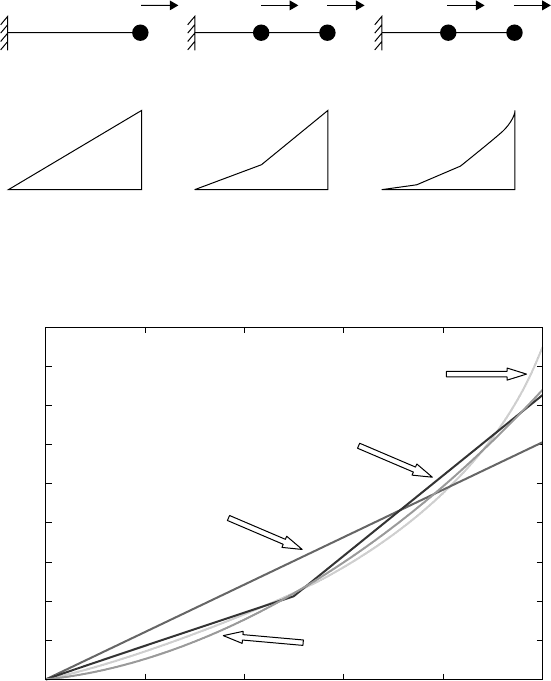
Figure 13.3 shows the ﬁnite element models and assumed shape functions.

Using the appropriate shape functions, forming the stiffness matrices using Eq. (13.12), and then solving

for the displacements and stresses for each problem, we obtain the displacement and stress results shown

in Figure 13.4 and Figure 13.5.

There are some important things to notice about the results. First let us look at the displacement plots

(see Figure 13.4). The exact displacement is the natural log function given in Eq. (13.15). The assumed

displacement functions try to approximate this function by a linear, bilinear, and a quadratic function,

respectively. The FEM states that you can use the linear function, but in the limit as the number of linear

segments goes to inﬁnity, the answer will be exact. You can see that the bilinear is a better approximation

than the linear. A trilinear would be even better, and so on. Also, the quadratic is even better than the other

two at approximating the natural log function.

Next we will look at the stresses (see Figure 13.5); here we see an even more dramatic result. The stress in

each linear element is constant. This is obvious since the stress is proportional to the strain and the strain

is the derivative of the displacement. Another fact about ﬁnite elements is that it is a displacement-based

method. This assumes that the displacements are continuous. However, it generally says nothing about the

One displacement

linear

Two displacements

bilinear

Two displacements

quadratic

FIGURE 13.3 Three shape function models for tapered section.

0.002

0.004

0.006

0.008

0.01

0.012

0.014

0.016

0.018

0 20406080100

Single linear element

Single quadratic element

Two linear elements

Exact

FIGURE 13.4 Axial displacement result for tapered element models.

13-6 Handbook of Dynamic System Modeling

0 20 40 60 80 100

Exact

Single quadratic element

Single linear element

Two linear elements

FIGURE 13.5 Axial stress for different tapered element models.

strain or stress. The displacement is continuous but the stresses are not continuous. This can be seen from

the bilinear result. The stresses are constant but different between the two halves of the tapered element

sections.

Finally, note that the stress from the quadratic element is linear. Again, this is due to the fact that the

stress is proportional to the derivative of the displacement. Note how in all the cases, the ﬁnite element

stress underestimated the true stress. Elements can be derived that also have stress continuity, but these

are more complex.

13.1.4 Shape Function Accuracy

In summary, the accuracy of a ﬁnite element is dependent on the choice of the shape function for that

element and the number of elements used in the model. In the limit, as the number of elements approach

inﬁnity, the model will give exact results. The displacements are assumed to be continuous between elements.

However, stresses are not continuous between elements.

The best accuracy is achieved with many higher order elements. Equal accuracy can be achieved by

a larger number of lower order elements. Clearly, the required number of elements depends on the

displacement ﬁeld you are trying to match. A linear displacement ﬁeld only needs linear elements.

13.1.5 Numerical Integration

In the previous section, we saw how the choice of the number of unknowns dictated the order of the

ﬁnite element shape function. The more nodes and unknowns used in the element, the higher the order.

Once the shape function is chosen, the element can be formed by performing an integral over the element

volume. In simple elements, this integration is easy to perform exactly. However, when we use irregular

shaped elements in two and three dimensions, it is very difﬁcult to perform the integration exactly.

As a result, most ﬁnite element programs rely on numerical integration techniques. Most engineers are

familiar with Trapezoidal and Simpson’s rule for numerical integration. While these methods are easy to

understand, they are computationally inefﬁcient. Instead, in ﬁnite element codes, the Gauss–Legendre

quadrature method is often used.

Gauss–Legendre quadrature is exact for simple polynomials and requires very little computation. The

basic formula for the method is



−1

F(x)dx =

number of points



i=1

∗F(µ

) (13.16)

Finite Elements 13-7

This formula says that to get the integral for a function F(x), you just need to sum the function at some

given evaluation points, µ

, times some weighting values, A

, for the given number of evaluation points.

Both the evaluation points and the weights are known numbers! It turns out that the weights (A

) and the

evaluation points (µ

) never change. As an example, the two point Gauss–Legendre quadrature points and

weights are

√

=−

√

(13.17)

= A

= 1.0

These formulas say that if the function to be integrated is evaluated at the two Gauss–Legendre points and

the results are summed you get the exact integral (from −1to1).

The Gauss–Legendre quadrature procedure is EXACT depending on the number of points used for the

sum. In the case above, for two-point integration, the method is exact for up to a cubic equation. The

formula for exactness is P =2N −1, where P is the order of the polynomial that can be integrated exactly

using N Gauss–Legendre sampling points.

Therefore, three Gauss–Legendre points (N =3) is exact for up to a ﬁfth-order polynomial. The Gauss–

Legendre points do not have to be rederived once they are found. As a matter of fact, they can be looked

up in many sources for up to 20 points.

It is clear that this method requires a very small number of function evaluations to get exact integration

results. Also note that the method is deﬁned as integrating a function from (−1 to 1). This restriction can

be lifted by using the mapping formula:



F(x) =

(B −A)

number of points



i=1



B −A

x +

B +A



(13.18)

This formula takes the points deﬁned on (−1 to 1) and shifts and scales (or maps) them into the new

limits, A to B. Using the mapping method also has some additional beneﬁts. Most ﬁnite element programs

deﬁne their element on this −1 to 1 coordinate system. Then, whatever the actual shape of the element, it

is mapped to the −1 to 1 system. This allows us to use nonrectangular shaped elements. The mapping of a

nonrectangular element into a −1 to 1 coordinate system develops the isoparametric ﬁnite element.

This same mapping and integration procedures are used in two and three dimensions. When going to

more dimensions, we need to extend the Gauss–Legendre quadrature scheme. The usual method is to use

the same points as in the 1-D case but in all coordinate directions.

13.1.6 Mapping Errors

There can also be problems when using the mapping to shift to a −1 to 1 coordinate system. In

isoparametric elements, the mapping procedure uses the displacement shape functions as mapping

functions. Therefore, any real location X in the element can be found from its −1 to 1 coordinate by the

formula:

X =



i=1

(µ)X

(13.19)

where H(µ)

is the shape function for nodes i and X

is the coordinate for node i. This mapping will work

for (1-D, 2-D, 3-D) elements. If we look at the 1-D axial problem again, we can develop the coordinate

mapping for the quadratic (two-node) element. If we allow the midpoint node to move between 1/4

13-8 Handbook of Dynamic System Modeling

from the left past the midpoint and 1/4 of the distance to the right end, we get the mapping as shown in

Figure 13.6.

Note in Figure 13.6 that if the midpoint node is either larger than 3/4 or smaller than 1/4, the mapping

goes outside the actual length of the element. This has the effect of saying that more than one location on

the element maps to the same point in the real X coordinate.

Clearly, this is not a valid element conﬁguration. It also means the element mapping is not valid because

it is not invertible. The mapping from one coordinate to the other is handled by a transformation matrix

called the Jacobian. The Jacobian matrix needs to be inverted to switch from one coordinate system to the

other. The validity of a mapping can be determined by the invertibility of this mapping matrix. Therefore,

if the Jacobian matrix is singular or noninvertible, then the mapping is not valid. This usually means that

the nodes are not in the correct locations, outside the 1/4 points, or there are bad nodal coordinates.

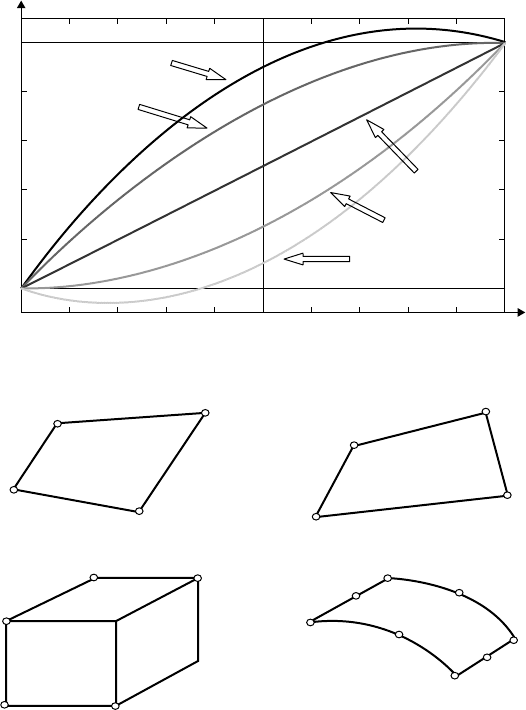
13.1.7 Available Elements

Energy derivations (e.g., virtual work) are commonly used to form the stiffness for a variety of element

types. The most common stiffness elements are the membrane (planar), plate, shell, and solid elements.

Each of these elements has a given set of nodes and displacements associated with those nodes. The

common forms of these elements are given in Figure 13.7.

100

1

0.75

0.5

0.25

<0.25

>0.75

0.8 0.6 0.4 0.2 0 0.2 0.4 0.6 0.8 1

FIGURE 13.6 Mapping with midpoint node not at the center.

Four-node membrane

Four-node plate

Eight-node-curved shell

Eight-node solid

FIGURE 13.7 Common ﬁnite elements.

Finite Elements 13-9

These elements have additional restrictions on their behavior that depend on their derivation. However,

the result is always a stiffness matrix that can then be treated like any other stiffness matrix and may be

rotated and transformed as desired. When combining these elements, the same concerns about boundary

conditions and matching DOF at the nodes must be accounted for. Additional concerns are also generated

since the shape function assumption can affect the accuracy of the results.

13.2 Membrane Elements

Membrane elements can be used to describe any continuum problem that is 2-D in nature. Either the

plane stress or plane strain condition can be modeled using these elements. The plane strain condition says

the out-of-plane strain is zero, and the plane stress condition says the out-of-plane stress is zero.

As an example, the following problems can be analyzed in 2-D using membrane elements (Figure 13.8).

13.2.1 Membrane Theory

The membrane element is a ﬂat element. It is generally assumed to have constant thickness. It can be

triangular, rectangular, four-sided polygonal, or have curved sides. The element is generally found in

conﬁgurations of three, four, six, eight, nine, and variable 3–9 nodes. Whatever the shape or number of

nodes, the element has two translational DOFs per node. These DOFs must lie in the plane of the element.

The results from the element consist of two normal stresses and a shear stress in the plane of the element

(see Figure 13.9). The stress results are generally given at each node in the element.

The difference in element behavior is dictated by the choice of the number of nodes and hence the num-

ber of DOFs for the element. The three-node triangle has linear shape functions and hence constant strain

and stress. This element is referred to as the constant strain triangle. The four-node element has a slightly

better response than the three-node element. The six-node triangle has quadratic shape functions and

linear stress and strain. The eight- and nine-node element has better response than the six-node element.

13.2.2 2-D Shape Functions

Remember, the shape function describes how the nodal displacements are distributed throughout the

element. In the membrane element, the X and Y displacements are assumed to be independent. As a

result, the same shape functions are reused for the X and Y displacements. The three-node elements have

linear shape functions for displacement. The four-node element adds an XY term to the shape function.

Rock

Soil

Tapered beam

Pavement

Concrete

dam

FIGURE 13.8 2-D problems using membrane.

13-10 Handbook of Dynamic System Modeling

Displacement DOF

Stress results

 0

FIGURE 13.9 Membrane DOF and stress results.

Four-node element Nine-node element

No shear at Gauss point

Shear at Gauss point

FIGURE 13.10 Shear locking of membrane.

The nine-node element has a quadratic variation of displacement. Remember the stress is the derivative

of the shape function and hence it will be linear with some quadratic parts.

The order of the shape functions are given to reinforce the capabilities of the particular elements

to model displacements. The more nonlinear the displacement ﬁeld in a problem, the more elements

required (like the tapered axial problem). In addition, higher order elements can approximate a more

complex displacement ﬁeld with fewer elements.

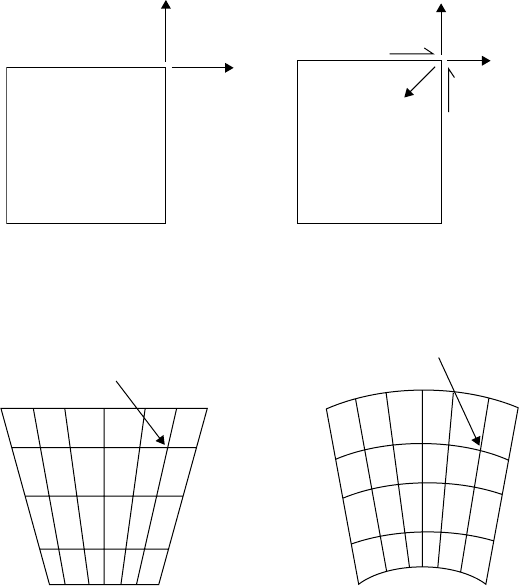
13.2.3 Shear Locking

When using or developing the FEM, the goal is to reduce the number of unknowns (nodes) and get

the highest order displacement behavior possible. Often, modeling complex behavior using lower order

elements can cause unexpected behavior. The problem with the four-node element (and all lower order

elements) lies in how the element models a higher order displacement ﬁeld like the bending (ﬂexural)

effect. Figure 13.10 gives the displaced shapes that each element uses to approximate beam bending.

The four-node element can only model bending (cubic displaced shape) by linear displacements. The

nine-node element has quadratic capabilities. The linear displaced shape causes shear to occur in the

element while in true bending none exists. The nine-node element does not generate this ﬁctitious shear.

This phenomenon is called shear locking. Four-node elements exist that do not exhibit this problem. By

changing the formulation, you can create an element that gives better behavior. The two most common

methods are by creating a nonconforming element or by using reduced integration. A nonconforming

element adds additional shape functions that contain the higher order (bending) shape (see Figure 13.11).

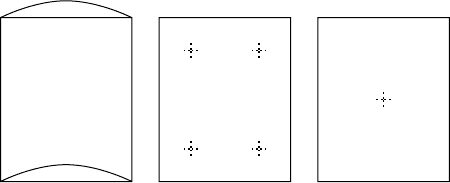
Finite Elements 13-11

Extra shape function Normal strain

integration point

Nonconforming element Reduced integration

Shear strain

integration point

FIGURE 13.11 Methods for removing shear locking.

However, this additional shape function is NOT continuous across element boundaries and hence dis-

placements are not continuous. Therefore, the effect is to allow gaps to open between elements. Reduced

integration uses a different number of Gauss–Legendre points during the integration, a number less than

that required for exact integration. The sampling points are chosen so that this shear is not included. For

the current example, a single point in the center of the element is used for integrating the shear terms. As

can be seen, this will neglect the shear developed in the element as a result of the linear displaced shape.

There are other more complex constraint processes that remove the shear locking problem.

13.2.4 Mesh Correctness and Convergence

As discussed in Section 13.1, the accuracy of the solution depends on the number of elements and the order

of the shape functions. As the number of elements increases, the piecewise displacement approximation

approaches the true displacement ﬁeld. Recall that two linear elements provided a better response than a

single linear element. Also, a single quadratic element performed even better.

13.2.5 Stress Difference to Indicate Mesh Accuracy

The stress results also follow the same pattern. More elements provide better stress results. However, since

we only guarantee the continuity of the displacements, the stresses are discontinuous. This means that at a

node where two elements meet, the stresses do not match. However, as the number of elements increases,

the difference in stresses between elements gets smaller. As an example, Figure 13.12 is a plot of the stress

along the top of the cantilever beam. The results are plotted for 4-4, 2-9, and 40-4 node membranes.

Note that for the 4-4-node elements, the difference between the elements is 28%. This large percentage

error indicates a poor mesh (or not enough elements). Looking at the two nine-node model we see a closer

difference. Here the error is 14%. This indicates that the mesh is marginal but probably sufﬁcient. Finally,

we look at the 40-element model. Here the error is much better and only 3%. The 40-element model is

very good. Note that many solution techniques perform another process of stress averaging to improve

the ﬁnal presented result.

The difference in element stresses at a node is an important measure of model correctness. In general, we

do not have the exact displacements to compare and check our model. Hence, stress checks are necessary

to verify convergence of our model. If the difference in stresses between elements is small, the ﬁnite element

mesh is good.

13.2.6 Element Meshing

Deﬁning a mesh is critical to ﬁnding a correct solution with a minimum number of elements. More

elements are needed where the displacement ﬁeld is highly nonlinear (or in a high stress gradient area).

13-12 Handbook of Dynamic System Modeling

4-4 node

40-4 node

2-9 node

FIGURE 13.12 Stress error for different mesh and shape function.

Constant stress

Stress variation

Increasing number of elements

Required meshing

FIGURE 13.13 Mesh variation with stress gradient.

Fewer elements are needed as the response becomes linear and only a single element is required in a constant

stress ﬁeld. As an example, the following stress function could be modeled by the mesh given in Figure13.13.

This change in the number of elements is handled by mesh changes from a single to multiple or higher

order elements. This is where variable node elements are useful.

Another important principle is that stress concentrations are localized phenomena and do not affect

the solution at a reasonable distance from the concentration. In other words, bad stress differences at one

portion of a model do not necessarily affect the results in a well-modeled portion.

In summary, a small stress difference between elements means a good mesh. Large stress differences in

localized areas will not necessarily affect the result a reasonable distance away.

13.3 Flat Plate and Shell Elements

The next ﬁnite element we examine is the ﬂat plate bending element. This element can be thought of

as a 2-D extension of a beam element. Beam elements provide both shear and bending resistance. Plate

elements provide this same resistance but in two directions.

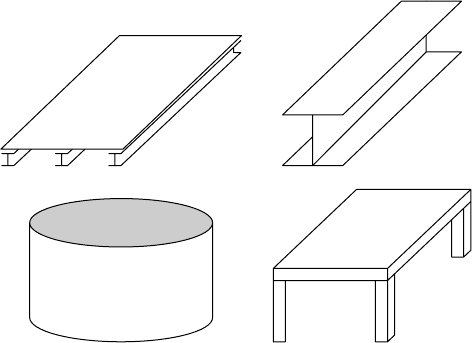
Finite Elements 13-13

Tank

Bridge

I Beam

Floor

slab

FIGURE 13.14 Structures where ﬂat places can be used.

Plate bending elements can be used to model common structural elements such as ﬂoor slabs, ﬂoor

diaphragms, bridge decks, and even I-beams. Wheneverout-of-plane bending effects need to be considered,

plate elements can be used. They are also useful for thin-walled structures like pipes and tanks. Most

modeling situations require that both the out-of-plane plate bending and in-plane membrane effects be

modeled. Some example structures are shown in Figure 13.14 that use plate and membrane elements.

True plate elements do not include in-plane effects. In-plane effects are handled by membrane elements.

Similarly in a beam element the bending and axial effects are uncoupled. This is the same in two dimensions.

These two elements are commonly merged to get a complete in-plane and out-of-plane element referred

to as a ﬂat shell element. A curved shell element would be needed to include the coupling of axial and

bending effects. We will discuss a true plate element before discussing ﬂat shell elements.

13.3.1 Plate Theory

Thereare two common versions of plate theoryused in ﬁnite elements: Kirchoff and Mindlin. Kirchoff plate

bending theory is derived in a similar fashion to beam bending but includes bending in both directions.

The derivation assumes that the normal displacement, w, controls. In Kirchoff theory the rotation, ,in

the plate is the derivative of w, the vertical displacement. This is the same as Euler–Bernoulli beam theory.

In Mindlin theory, shear deformation is included and the rotation is the sum of the derivative of w and

the shear deformation angle.

13.3.1.1 Kirchoff Theory

In Kirchoff theory, the normal to the surface remains normal. Hence, this theory ignores shear deformations

(just like Euler–Bernoulli beam theory). To derive this type of ﬁnite element, a shape function that describes

the distribution of the normal displacement w(x, y) throughout the element is needed. This shape function

has the property that its derivative is equal to the slope of the surface. An important implication of this is

that the slope is continuous across elements! This is called a C

element, meaning that it has continuous

ﬁrst derivatives between elements. Figure 13.15 shows the relationship between w and  for Kirchoff

theory.

13.3.1.2 Mindlin Theory

The second theory, Mindlin, includes shear deformations. As a result, a vector initially normal to the

surface does not remain normal during deformation. The derivative of the shape function for the normal

displacement w(x, y)isnot equal to the rotation. In Mindlin theory, the rotation of the surface is the sum