Fishwick P.A. (editor) Handbook of Dynamic System Modeling
Подождите немного. Документ загружается.

11-18 Handbook of Dynamic System Modeling
class ClawInteg: public Integrator, public cell_interface {
public:
ClawInteg(double q0, int index, double D, double∗ x, double dx):
Integrator(q0,index,D,x),cell_interface(){ ClawInteg::dx=dx; }
double f(int index, const double∗ x) {
return 0.5∗(x[index−1]∗x[index−1]−x[index]∗x[index])/dx;
}
private:
static double dx;
};
double ClawInteg::dx = 0.0;
FIGURE 11.12 Integrator for the conservation law simulation.
0.2
0
0.2
0.4
0.6
0.8
1
0 2 4 6 8 10 12
u (t, x )
x
t 0
t 5
t 10
t 15
(a) (b)
0
0.2
0.4
0.6
0.8
1
02468 10 12
u (t , x )
x
t 0
t 5
t 10
t 15
(c)
0
0.2
0.4
0.6
0.8
1
024681012
u (t, x )
x
t 0
t 5
t 10
t 15
FIGURE 11.13 Simulation of Eq. (11.17) with various quantum sizes. (a) D =0.1, (b) D =0.01, and (c) D =0.001.
1e04
0.001
0.01
0.1
1
10
100
1000
0123456789 10
State update frequency
x
t 0
t 5
t 10
t 15
(a)
1
10
100
1000
10,000
012345678910
Total number of state transitions
x
t 0
t 5
t 10
t 15
(b)
FIGURE 11.14 Front tracking in the DEVS simulation of Eq. (11.17) with D =0.001. (a) Update frequency, and
(b) State transition count.
larger derivatives follow the shock, with the area in front of the shock having zero derivatives and the area
behind the shock having diminished derivatives. The DEVS simulation apportions computational effort
appropriately. This is shown in Figure 11.14 for a simulation with D =0.001. Figure 11.14(a) shows several
snapshots of the cell update frequency (i.e., ˙u(ix, t)/D following an internal event, where i is the gridpoint
index) at times corresponding to the solution snapshots shown in Figure 11.13(c). Figure 11.14(b) shows
the total number of state transitions computed at each cell at those times. The effect of this front-tracking
behavior on the simulation running time can be significant. In Nutaro et al. (2003), it is responsible for a
speedup of 35 relative to a discrete time solution for Euler’s equations in one spatial dimension.

Discrete-Event Simulation of Continuous Systems 11-19
11.7 Two-Point Integration Schemes
The integration scheme discussed to this point is a single point scheme. It relies on a single past value of
the function, and it is exact for the linear equation ˙x(t) =k,wherek is a constant. Recall that the single
point scheme for simulating a system ˙x(t) =f (x(t)) can be derived from the expression
t
0
+h
t
0
f (x(t))dt
= D (11.18)
by approximating f (x(t)) with the value f (x(t
0
)).
If the function f (x(t)) in Eq. (11.18) is approximated using the previous two values of the derivative,
then the resulting method is called a two-point scheme. A DEVS model of a two-point scheme requires
the state variables
q, the current approximation to x(t);
q
l
, the last grid point occupied by q;
σ, the time required to move from q to the next grid point;
˙q
1
and ˙q
0
, the last two computed values of the derivative; and, possibly,
h, the time interval between ˙q
1
and ˙q
0
.
At least two different two-point methods have been described (see Kofman, 2004; Nutaro, 2005). The
first method approximates f (x(t)) in Eq. (11.18) with the line connecting points ˙q
1
and ˙q
0
. The distance
moved by x(t) in the interval [h, h +T] can be approximated by
h+T
h
˙q
1
−˙q
0
h
+˙q
0
dt =
˙q
1
−˙q
0
2h
T
2
+˙q
1
T = q
The functions
ˆ
F
1
(T, ˙q
1
, ˙q
0
, h) =
˙q
1
−˙q
0
2h
T
2
+˙q
1
T (11.19)
and
ˆ
F
−1
1
(q, ˙q
1
, ˙q
0
, h) = T (11.20)
where T is the smallest positive root of
˙q
1
−˙q
0
2h
T
2
+˙q
1
T
= q
or ∞ if such a root does not exist, can be used to define the state transition, output, and time advance
functions (which will be done in a moment). Eq. (11.19) and Eq. (11.20) are exact when x(t) is quadratic.
The second method approximates f (x(t)) with the piecewise constant function
a˙q
1
+b˙q
0
, a + b = 1 (11.21)
If x(t) is the line mt +b, then f (x(t)) =m,(am +bm) =(a +b)m =m, and so this approximation is exact.
Integrating Eq. (11.21) over the interval [0, T] gives the approximating functions
ˆ
F
2
(T, ˙q
1
, ˙q
0
) = (a˙q
1
+b˙q
0
)T (11.22)
ˆ
F
−1
2
(q, ˙q
1
, ˙q
0
) =
q
|a˙q
1
+b˙q
0
|
(11.23)
This approximation does not require the state variable h.

11-20 Handbook of Dynamic System Modeling
For brevity, let ¯q denote the state of the integrator, and
¯
dq denote the variables ˙q
1
, ˙q
0
or ˙q
1
, ˙q
0
, h as
needed. Which is intended will be clear from the context in which it is used. The time advance function
for a two-point scheme is given by
ta(¯q) = σ
and the output function is defined by
λ(¯q) =
ˆ
F(σ,
¯
dq)
If Eq. (11.19) and Eq. (11.20) are used to define the integration scheme, then the resulting state transition
functions are
δ
int
(¯q) = (q +
ˆ
F
1
(σ,
¯
dq), q +
ˆ
F
1
(σ,
¯
dq), q
1
, q
1
, σ,
ˆ
F
−1
1
(D, ˙q
1
, ˙q
1
, σ))
δ
ext
(¯q, e, x) = (q
l
, q +
ˆ
F
1
(e,
¯
dq), x, q
1
, e,
ˆ
F
−1
1
(D −|q +
ˆ
F
1
(e,
¯
dq) −q
l
|, x, ˙q
1
, e))
δ
con
(¯q, x) = (q +
ˆ
F
1
(σ,
¯
dq), q +
ˆ
F
1
(σ,
¯
dq), x, q
1
, σ,
ˆ
F
−1
1
(D, x, ˙q
1
, σ))
When Eq. (11.22) and Eq. (11.23) are used to define the integrator, then the state transition functions are
δ
int
(¯q) = (q +
ˆ
F
2
(σ,
¯
dq), q +
ˆ
F
2
(σ,
¯
dq), q
1
, q
1
,
ˆ
F
−1
2
(D, ˙q
1
, ˙q
1
))
δ
ext
(¯q, e, x) = (q
l
, q +
ˆ
F
2
(e,
¯
dq), x, q
1
,
ˆ
F
−1
2
(D −|q +
ˆ
F
2
(e,
¯
dq) −q
l
|, x, ˙q
1
))
δ
con
(¯q, x) = (q +
ˆ
F
2
(σ,
¯
dq), q +
ˆ
F
2
(σ,
¯
dq), x, q
1
,
ˆ
F
−1
2
(D, x, ˙q
1
))
The scheme that is constructed using Eq. (11.19) and Eq. (11.20) is similar to the QSS2 method in
Kofman (2004), except that the input and output trajectories used here are piecewise constant rather than
piecewise linear.
The scheme constructed from Eq. (11.22) and Eq.(11.23) is nearly second-order accurate when a and
b are chosen correctly. If a =
3
2
and b =−
1
2
, then the error, with respect to Eq. (11.18), in the integral of
Eq. (11.21) is
E =
f (x
1
) −
3f (x
1
)
2
+
f (x
0
)
2
T +
1
2
T
2
d
dt
f (x
1
) +
∞
n=3
1
n!
d
dt
(n)
f (x
1
)T
n
(11.24)
For this scheme to be nearly second-order accurate, the terms that depend on T and T
2
need to be as
small as possible. Let h be the time separating x
1
and x
0
(i.e., x
1
=x(t
1
), x
0
=x(t
0
), and h =t
1
−t
0
), and
let α =
T
h
, the ratio of the current time advance to the previous time advance. It follows that T =αh.The
function
d
dt
f (x
1
) can be approximated by
d
dt
f (x
1
) ≈
f (x
1
) −f (x
0
)
h
(11.25)
Substituting Eq. (11.25) into Eq.(11.24) and dropping the high-order error terms gives
E ≈ αh
f (x
1
) −f (x
0
)
2
+α
f (x
0
) −f (x
1
)
2
(11.26)
Eq. (11.26) approaches 0 as α approaches 1. It seems reasonable to assume T and h become increasingly
similar as D is made smaller. From this assumption, it follows that the low-order error terms in Eq. (11.24)
vanish as D shrinks.
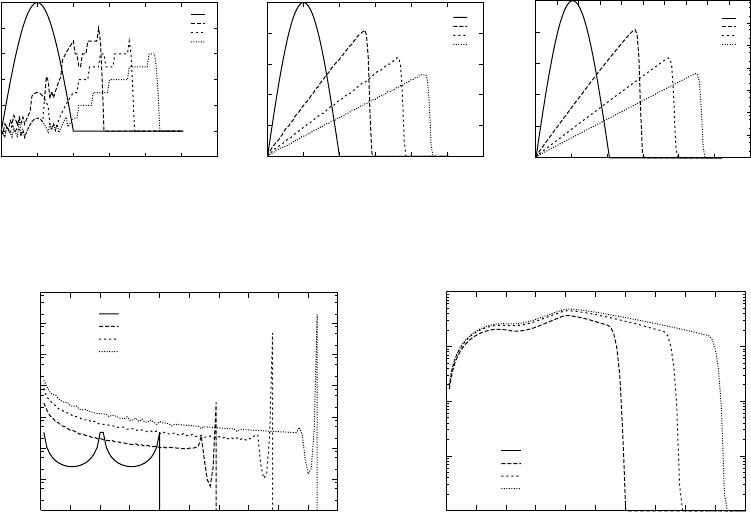
Figure 11.15(a) and Figure 11.15(b) show the absolute error in the computed solution of ˙x(t) =−x(t),
x(0) =1, as a function of D for these two integration schemes. The simulation is ended at t =1.0, and
Discrete-Event Simulation of Continuous Systems 11-21
0
0.001
0.002
0.003
0.004
0.005
0.006
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
Absolute error
D
(a)
0
0.0005
0.001
0.0015
0.002
0.0025
0.003
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
Absolute error
D
(b)
FIGURE 11.15 Simulation error as a function of D for the system ˙x(t) =−x(t) with x(0) =1. (a) Simulation error
using Eq. (11.19) and Eq. (11.20). (b) Simulation error using Eq. (11.22) and Eq. (11.23).
α and the absolute error are recorded at that time. In both cases, it can be observed that the absolute error
is proportional to D
2
.
These two schemes use additional information to reduce the approximation error with respect to the
single point scheme. Fortunately, these two schemes share the unconditional linear stability of the single
point scheme (see Kofman, 2004; Nutaro, 2003), and so they represent a tradeoff between storage, execution
time, and accuracy. When dealing with very large systems, the single point scheme has the advantage of
needing less computer memory because it has fewer state variables per integrator. However, it will, in
general, be less accurate than a two-point scheme for a given quantum size. If the quantum size is selected
to obtain a given error, then the two-point scheme will generally use a larger quantum than the one-point
scheme, and so the simulation will finish more quickly using the two-point scheme.
11.8 Conclusions
This chapter introduced some essential techniques for constructing discrete-event approximations to
continuous systems. Discrete-event simulation of continuous systems is an active area of research, and
the breadth of the field cannot be adequately covered in this short space. In the conclusion, some related
research is summarized, and references are given, for the interested reader.
A side-by-side introduction of discrete time and discrete-event methods for continuous system sim-
ulation can be found in Cellier and Kofman (2006). Comparisons of nonadaptive discrete time and
discrete-event methods can be found in Muzy et al. (2005), Nutaro et al. (2003), Zeigler (2004), and Kof-
man (2004). In-depth comparison of discrete-event schemes with adaptive time stepping, asynchronous,
and other types of advanced numerical integration methods remains a topic for future research.
The construction of high-order discrete-event integration schemes is discussed in Nutaro (2005).
A third-order scheme, and the only third-order method developed to date, is described in Kofman
(2005a, 2005b).
In Bolduc and Vangheluwe (2003), an adaptive quantum scheme is introduced. This scheme allows the
integration quantum to be varied during the course of the calculation to maintain an upper bound on
the global error. An application of adaptive quantization to a fire-spreading model is discussed in Muzzy
et al. (2002).
A methodology for approximating general time functions as DEVS models is discussed in Giambiasi et al.
(2000). The approximations introduced in that paper associate events with changes in the coefficients of
an interpolating polynomial. An application of this methodology to partial differential equations is shown
in Wainer and Giambiasi (2005).
11-22 Handbook of Dynamic System Modeling
Applying DEVS models to finite element methods for equilibrium problems is discussed in D’Abreu and
Wainer (2003) and Saadawi and Wainer (2004). A steady state heat transfer problem is used to demonstrate
the method.
Simulation of partial differential equations leads naturally to parallel computing. Parallel discrete-event
simulation for the numerical methods presented in this chapter are discussed in Nutaro (2003) and Nutaro
and Sarjoughian (2004). Specific issues that emerge when simulating DEVS models using logical process-
based algorithms are described in Nutaro and Sarjoughian (2004). Parallel discrete-event simulation
applied to particles in cell methods is discussed in Tang et al. (2005) and Karimabadi et al. (2005).
References
Bolduc, J.-S. and H. Vangheluwe (2003). Mapping ODEs to DEVS: Adaptive quantization. In Proceedings
of the 2003 Summer Simulation MultiConference (SCSC’03), Montreal, Canada, pp. 401–407.
Cellier, F. E. and E. Kofman (2006). Continuous System Simulation. New York: Springer.
D’Abreu, M. and G. Wainer (2003). Improving finite elements method models using cell-DEVS. In
Proceedings of the 2003 Summer Computer Simulation Conference, Montreal, QC, Canada.
Filippi, J.-B. and P. Bisgambiglia (2004). JDEVS: An implementation of a DEVS based formal framework
for environmental modeling. Environmental Modelling & Software 19(3), 261–274.
Giambiasi, N., B. Escude, and S. Ghosh (2000). GDEVS: A generalized discrete event specification for accu-
rate modeling of dynamic systems. Transactions of the Society Computer Simulation International
17(3), 120–134.
Hwang, K. (1993). Advanced Computer Architecture: Parallelism, Scalability, Programmability.NewYork:
McGraw-Hill.
Jammalamadaka, R. (2003). Activity characterization of spatial models: Application to the discrete
event solution of partial differential equations. Master’s thesis, University of Arizona, Tucson,
Arizona, USA.
Karimabadi, H., J. Driscoll, Y. Omelchenko, and N. Omidi (2005). A new asynchronous methodology for
modeling of physical systems: Breaking the curse of the Courant condition. Journal of Computational
Physics 205(2), 755–775.
Kofman, E. (2004). Discrete event simulation of hybrid systems. SIAM Journal on Scientific Computing
25(5), 1771–1797.
Kofman, E. (2005a). A third order discrete event method for continuous system simulation. Part I: Theory.
In Proceedings of RPIC’05.
Kofman, E. (2005b). A third order discrete event method for continuous system simulation. Part II:
Applications. In Proceedings of RPIC’05.
Kofman, E., M. Lapadula, and E. Pagliero (2003). PowerDEVS: A DEVS-based environment for hybrid
system modeling and simulation. Technical Report LSD0306, School of Electronic Engineering,
Universidad Nacional de Rosario, Rosario, Argentina.
Kroner, D. (1997). Numerical Schemes for Conservation Laws. Chichester, NY: Wiley.
Muzy, A., E. Innocenti, A. Aiello, J.-F. Santucci, and G. Wainer (2002). Cell-DEVS quantization techniques
in a fire spreading application. In Proceedings of the 2002 Winter Simulation Conference, Sandiego,
CA.
Muzy, A. and J. Nutaro (2005). Algorithms for efficient implementations of the DEVS & DSDEVS abstract
simulators. In 1st Open International Conference on Modeling & Simulation, ISIMA/Blaise Pascal
University, France, pp. 401–407.
Muzy, A., P.-A. Santoni, B. P. Zeigler, J. J. Nutaro, and R. Jammalamadaka (2005). Discrete event simulation
of large-scale spatial continuous systems. In IEEE International Conference on Systems, Man, and
Cybernetics, Vol. 4, Waikoloa, Hawaii, pp. 2991–2998.
Nutaro, J. (2003). Parallel discrete event simulation with application to continuous systems. Ph.D. thesis,
University of Arizona, Tuscon, Arizona.
Discrete-Event Simulation of Continuous Systems 11-23
Nutaro, J. (2005). Constructing multi-point discrete event integration schemes. In Proceedings of the 2005
Winter Simulation Conference, Orlando, FL.
Nutaro, J. and H. Sarjoughian (2004). Design of distributed simulation environments: A unified system-
theoretic and logical processes approach. Simulation 80(11), 577–589.
Nutaro, J. J., B. P. Zeigler, R. Jammalamadaka, and S. R. Akerkar (2003). Discrete event solution of
gas dynamics within the DEVS framework. In P. M. A. Sloot, D. Abramson, A. V. Bogdanov,
J. Dongarra, A. Y. Zomaya, and Y. E. Gorbachev (Eds.), International Conference on Computational
Science, Volume 2660 of Lecture Notes in Computer Science, pp. 319–328. Berlin: Springer.
Saadawi, H. and G. Wainer (2004). Modeling complex physical systems using 2D finite elemental cell-
DEVS. In Proceedings of MGA, Advanced Simulation Technologies Conference 2004 (ASTC’04),
Arlington, VA, USA.
Strang, G. (1986). Introduction to Applied Mathematics. Wellesley, MA: Wellesley-Cambridge Press.
Szidarovszky, F. and A. T. Bahill (1998). Linear Systems Theory, 2nd edition. Boca Raton, FL: CRC
Press LLC.
Tang, Y., K. Perumalla, R. Fujimoto, H. Karimabadi, J. Driscoll,and Y. Omelchenko (2005). Parallel discrete
event simulations of physical systems using reverse computation. In ACM/IEEE/SCS Workshop on
Principles of Advanced and Distributed Simulation (PADS), Monterey, CA.
Wainer, G. (2002). CD++: A toolkit to develop DEVS models. Software: Practice and Experience 32(13),
1261–1306.
Wainer, G. A. and N. Giambiasi (2005). Cell-DEVS/GDEVS for complex continuous systems. Simulation
81(2), 137–151.
Zeigler, B. P. (2004). Continuity and change (activity) are fundamentally related in DEVS simulation of
continuous systems. In Keynote Talk at AI, Simulation, and Planning 2004 (AIS’04), Jeju, Korea.
Zeigler, B. P., H. Praehofer, and T. G. Kim (2000). Theory of Modeling and Simulation, 2nd edition.
New York: Academic Press.
Zeigler, B. P., H. Sarjoughian, and H. Praehofer (2000). Theory of quantized systems: DEVS simulation of
perceiving agents. Cybernetics and Systems 31(6), 611–647.
Zeigler, B. P. and H. S. Sarjoughian (2005). Introduction to DEVS modeling and simulation with JAVA:
Developing component-based simulation models. Unpublished manuscript.

III
Multiobject and
System
III-1

12
Toward a Multimodel
HierarchytoSupport
Multiscale Simulation
Mark S. Shephard
Scientific Computation Research Center
E. Seegyoung Seol
Scientific Computation Research Center
Benjamin FrantzDale
Scientific Computation Research Center
12.1 Introduction ................................................................ 12-1
12.2 Functional and Information Hierarchies in
Multiscale Simulation ................................................. 12-4
Mathematical Physics Description Transformations
and Interactions
•
Domain Definitions, Transformations,
and Interactions
•
Physical Parameter Definitions,
Transformations, and Interactions
12.3 Constructing a Multimodel: Design of Functional
Components to Support Multiscale Simulations ...... 12-10
Problem Definition
•
Equation Parameters
•
Geometric
Domain
•
Discretized Geometric Domains
•
Tensor
Fields
•
Scale-Linking Operators
12.4 Example Multimodel Simulation Procedures ........... 12-14
Automated Adaptive Mesh-Based Simulation
•
Adaptive
Atomistic/Continuum Adaptive Multiscale Simulation
12.5 Closing Remarks ......................................................... 12-15
12.1 Introduction
There is a long history of developing mathematical representations capable of providing behavioral pre-
dictions of physical parameters on the atomic, molecular, microscopic, and macroscopic scales. Over the
past half century, simulation programs have been developed to support the computerized solution of these
mathematical representations which, in some cases, are discretized with billions of degrees of freedom
(dofs) and solved on massively parallel computers with thousands of processors. Historically, scientists
and engineers have applied these models (simulation programs) to solve problems on a single physical
scale. However, in recent years it has become clear that to continue to make advances in the areas of nan-
otechnology and biotechnology, and to develop new products and treatments based on those advances,
scientists and engineers must be able to solve sets of coupled models active over multiple interacting scales.
For example, the development of new materials will require the design of structure and function across
a hierarchy of scales, starting at the molecular scale to define nanoscale building blocks that will be used
to construct mesoscale features that may be combined into micron-scale weaves that could be used in the
manufacturing of complete parts (Figure 12.1). Such capabilities are clearly central to the development of
nanoelectronics devices and future biomedical device design as well as many of other future products.
As an example of the potential impact of multiscale simulation on biomedical device design, consider a
drug-eluting stent (Figure 12.2). Drug-eluting stents are hybrid device–drug medical products that release
therapeutic drugs and provide a scaffold to maintain arterial lumen size after angioplasty. The design
12-1
