Fishwick P.A. (editor) Handbook of Dynamic System Modeling

Подождите немного. Документ загружается.

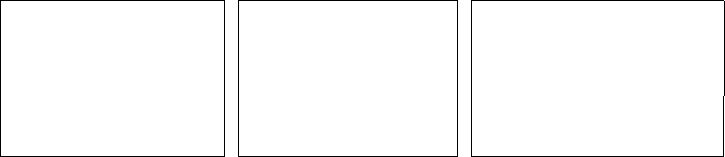
10-12 Handbook of Dynamic System Modeling

the lbts value (13) is being computed. Conservative simulation simply waits until the lbts value is

known. Optimistic simulation, on the other hand, goes ahead with processing the events A@10 and D@12

even while lbts is being computed. Suppose the lbts value is still being computed even after A@10

and D@12 are processed. The multiplexer continues its optimistic processing and processes D@15 as

well. Later, the event A@13 from source 1 arrives and lbts is advanced to 13. Clearly, D@15 has been

incorrectly processed ahead of A@13, and hence it needs to be corrected. The optimistic simulation then

initiates a corrective action called rollback, which restores the state of the system back to the point of fault,

namely to time 13. Once the rollback is completed, the incorrect effects of D@15 are fully undone, and

hence the system is effectively in the same position as though it only processed until D@12 and never

processed D@15. Event processing now resumes at A@13 correctly. The net gain is that the three events

D@9, A@10, and D@12 have all been already processed (correctly) without having to wait for the actual

lbts value. This overlap of computation with communication results in better concurrency in execution,

thus increasing the overall speed of simulation.

The key element enabling this type of optimistic operation is the capability to rollback incorrect com-

putation. For example, in our scenario, we assumed that the system state can be restored to its correct

value before D@15 even though we have already processed D@15 and overwritten the state with newly

computed values with D@15. How is it now possible to undo the effects of D@15? Also, D@15 scheduled a

new event which should also be retracted. In general, optimistically processed events overwrite the entity

state with newly updated values and also send out new events to other processors; all of these effects need

to be carefully undone to restore the state to correct values for complete rollback. Let us consider the two

distinct aspects of rollback: (1) state restoration and (2) event retraction.

For state restoration, several variants have been proposed, of which there are mainly two categories: (1)

state saving and (2) reverse computation. In the state saving method, a copy of the system state is saved

before it is modiﬁed in the optimistic event processing. In other words, a copy of the values of all system

variables is saved before being overwritten by the event handler code. In the multiplexer example, a copy

of all variables in Figure 10.17(a) is saved in a buffer before the departure event handler code of Figure

10.17(c) is invoked for the event D@15. A pointer to this buffer is stored in the event data structure of

D@15 itself. When it is necessary to rollback D@15, the buffer is retrieved using the pointer, and the old

values saved in the buffer are used to overwrite the multiplexer state variables, thus effectively restoring

the state to correct values before D@15 was incorrectly processed.

An alternative method for state restoration is called reverse computation (Carothers, 99). In this

approach, instead of using the copy-restore method, inverse event handlers are used to undo the effects

of incorrectly executed event handlers, on a statement-by-statement basis of the handler code, in reverse

order of invocation. For example, the inverse event handlers shown in Figure 10.17 are deﬁned and used

to undo incorrect invocations to event handlers.

A bit variable is added to the state to keep track of whether the “if”statement body has been evaluated in

the forward (incorrect) execution. This single bit variable, stored in the event data structure, is sufﬁcient

to later restore the rest of the variables to their correct previous values. This is achieved by deﬁning the

Integer qlen;

Integer sent;

Integer lost;

Integer delays[B];

bit b;

(a)

b=0

if qlen > 0

b=1

qlen--;

sent++;

send(cell);

(b)

ifb==1

retract(cell);

--sent;

++qlen;

(c)

FIGURE 10.17 Modiﬁed version of departure event handler of ATM multiplexer for reverse computation-based

rollback. (a) Modiﬁed state (one bit variable added). (b) Departure event handler—Forward. (c) Departure event

handler—Reverse.

Model Execution 10-13

reverse event handler shown in Figure 10.17(c). This is obtained by inverting the order of the statements

in the forward event handler in Figure 10.17(b) and inverting the operations within each statement.

Event retraction within a processor is relatively easily achieved, simply removing the event from local

priority queue data structure of event list. Retracting events that have been forwarded to other processors

is slightly more involved, which requires forwarding a retraction request to the destination processor.

Two cases arise: the retraction request arrives the destination processor after the original event already

has arrived at that processor; the retraction request arrives at the destination processor even before the

original event arrived at that processor. The ﬁrst case is easy to handle, since the original event is already

identiﬁable—the event is removed from the event list if it has not been processed, or it is ﬁrst rolled back

and then removed if it has been already processed. If the retraction arrives before the event arrives, the

retraction is simply buffered and until the actual event is received and then both the retraction and the

event are nulliﬁed.

10.3.3.3 Mixed-Mode Parallel Execution

In mixed-mode parallel execution, the system supports a mixture of optimistic and conservative execution

within each processor. Entities can specify whether their events are to be processed using optimistic

(rollback-based) synchronization or conservative (blocking-based) synchronization. As a result, the

simulation algorithm becomes considerably more complex and hence not discussed here.

10.4 Summary

Model execution involves computing the evolution of state values for a set of interacting entities in

a model over time. Computing the state evolution can be performed using different time advancing

techniques, and executed sequentially or in parallel. Popular techniques include time-stepped execution

and discrete-event execution. While sequential execution of time-stepped techniques can be parallelized

in a relatively straightforward manner, parallelization of discrete-event execution involves resolution of

important synchronization issues. Parallel discrete-event synchronization approaches broadly fall under

two categories: conservative and optimistic methods. This chapter described the time-stepped and discrete-

event methods with examples and presented algorithms for their implementation for sequential and

parallel execution.

References

Bagrodia, R., R. Meyer, M. Takai, Y. Chen, X. Zeng, J. Martin, B. Park, and H. Song. “Parsec: A Parallel

Simulation Environment for Complex Systems.” IEEE Computer, 31(10) (1998): 77–85.

Balci, O. “The Implementation of Four Conceptual Frameworks for Simulation Modeling in High-Level

Languages.” Paper presented at the Winter Simulation Conference, 1988.

Banks, J., J. S. Carson II, and B. L. Nelson. Discrete-Event System Simulation. Upper Saddle River, NJ:

Prentice-Hall, 1996.

Carothers, C., K. S. Perumalla, and R. M. Fujimoto. “Efﬁcient Optimistic Parallel Simulations Using

Reverse Computation.” ACM Transactions on Modeling and Computer Simulation, 9(3) (1999):

224–253.

Chandy, K. M. and R. Sherman. “Space, Time, and Simulation.” In Proceedings of the SCS Multiconference

on Distributed Simulation, pp. 53–57, SCS Simulation Series, 1989.

Das, S., R. M. Fujimoto, K. Panesar, D. Allison, and M. Hybinette. “GTW: A Time Warp System for Shared

Memory Multiprocessors.” In Proceedings of the 1994 Winter Simulation Conference, pp. 1332–1339,

1994.

Deelman, E., R. Bagrodia, R. Sakellariou, and V. Adve. “Improving Lookahead in Parallel Discrete

Event Simulations of Large-Scale Applications Using Compiler Analysis.” In Proceedings of the

15th Workshop on Parallel and Distributed Simulation, pp. 5–13, 2001.

10-14 Handbook of Dynamic System Modeling

Fishwick, P. A. Simulation Model Design and Execution: Building Digital Worlds, 1st ed., Englewood Cliffs,

NJ: Prentice-Hall, 1995.

Fujimoto, R. M. “Optimistic Approaches to Parallel Discrete Event Simulation.” Transactions of the Society

for Computer Simulation, 7(2) (1990a): 153–191.

Fujimoto, R. M.“Parallel Discrete Event Simulation.” Communications of the ACM, 33(10) (1990b): 30–53.

Fujimoto, R. M., I. Nikolaidis, and A. C. Cooper. “Parallel Simulation of Statistical Multiplexers.” Journal

of Discrete Event Dynamic Systems, 5 (1995): 115–140.

Nance, R. E. “The Time and State Relationships in Simulation Modeling.” Communications of the ACM,

24(4) (1981): 173–179.

Nance, R. E. “A History of Discrete Event Simulation Programming Languages.” ACM SIGPLAN Notices,

28(3) (1993): 149–75.

Nicol, D. and P. Heidelberger. “Parallel Execution for Serial Simulators.” ACM Transactions on Modeling

and Computer Simulation, 6(3) (1996): 210–242.

Nutaro, J. 2003. Adevs: A Discrete Event System Simulator. In http://www.ece.arizona.edu/∼nutaro

(accessed 2006/06/01).

Perumalla, K. S. and R. M. Fujimoto. “Efﬁcient Large-Scale Process-Oriented Parallel Simulations.” In

Proceedings of the Winter Simulation Conference, 459–466, 1998.

Pidd, M. “Object Orientation and Three Phase Simulation.” Paper presented at the Winter Simulation

Conference, Arlington, VA, 1992.

Schriber, T. J. Simulation Using GPSS. New York: Wiley, 1974.

To c h e r , K . D. The Art of Simulation. London: English Universities Press, 1963.

Zeigler, B. P., H. Praehofer, and T. G. Kim. Theory of Modeling and Simulation, 2nd ed., New York:

Academic Press, 2000.

Discrete-Event Simulation

of Continuous Systems

∗

James Nutaro

Oak Ridge National Laboratory

11.1 Introduction ................................................................ 11-1

11.2 Simulating a Single Ordinary Differential

Equation ...................................................................... 11-2

11.3 Simulating Coupled Ordinary Differential

Equations ..................................................................... 11-6

11.4 DEVS Representation of Discrete-Event

Integrators ................................................................... 11-8

11.5 The Heat Equation ...................................................... 11-13

11.6 Conservation Laws ...................................................... 11-16

11.7 Two-Point Integration Schemes ................................. 11-19

11.8 Conclusions ................................................................. 11-21

11.1 Introduction

Computer simulation of a system described by differential equations requires that some element of the

system be approximated by discrete quantities. There are two system aspects that can be made discrete:

time and state. When time is discrete, the differential equation is approximated by a difference equation

(i.e., a discrete-time system), and the solution is calculated at ﬁxed points in time. When the state is

discrete, the differential equation is approximated by a discrete-event system. Events correspond to jumps

through the discrete state space of the approximation.

The essential feature of a discrete time approximation is that the resulting difference equations map

a discrete time set to a continuous state set. The time discretization need not be regular. It may even be

revised in the course of a calculation. Nonetheless, the elementary features of a discrete time base and

continuous state space remain.

The basic feature of a discrete-event approximation is opposite that of a discrete time approxima-

tion. The approximating discrete-event system is a function from a continuous time set to a discrete

state set. The state discretization need not be uniform, and it may even be revised as the computation

progresses.

These two different types of discretizations can be visualized by considering how the function x(t),

shown in Figure 11.1(a), might be reduced to discrete points. In a discrete time approximation, the

value of the function is observed at regular intervals of time. This kind of discretization is shown in

∗

This chapter has been authored by UT-Battelle, LLC, under contract De-AC05-00OR22725 with the U.S. Depart-

ment of Energy. The United States Government retains and the publisher, by accepting the article for publication,

acknowledges that the Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or

reproduce the published form of this chapter, or allow others to do so, for the Government’s purposes.

11-1

11-2 Handbook of Dynamic System Modeling

(a)

(b) (c)

FIGURE 11.1 Time and state discretizations of a system. (a) Continuous, (b) Discrete time, and (c) Discrete state.

Figure 11.1(b). In a discrete-event approximation, the function is sampled when it takes on regularly

spaced values. This type of discretization is shown in Figure 11.1(c).

From an algorithmic point of view, these two types of discretizations are widely divergent. The ﬁrst

approach emphasizes the simulation of coupled difference equations. Some distinguishing features of

a difference equation simulator are nested “for” loops (used to compute function values at each time

step), single instruction multiple data (SIMD) type parallel computing (using, e.g., vector processors or

automated “for” loop parallelization, see Hwang, 1993), and good locality of reference.

The second approach emphasizes the simulation of discrete-event systems. The main computational

features of a discrete-event simulation are very different from a discrete time simulation. Foremost among

them are event scheduling, poor locality of reference, and multiple instruction multiple data (MIMD) type

asynchronous parallel algorithms (see, e.g., Hwang, 1993). The essential data structures are different, too.

Where difference equation solvers exploit a matrix representation of the system coupling, discrete-event

simulations often require different, but structurally equivalent, data structures (e.g., inﬂuence graphs).

Mathematically, however, they share several features. The approximation of functions via interpolation

and extrapolation are central to both. Careful study of error bounds, stability regimes, conservation

properties, and other elements of the approximating machinery is essential. It is not surprising that

theoretical aspects of differential operators, and their discrete approximations, have a prominent place in

the study of both discrete time and discrete-event numerical methods.

This conﬂuence of applied mathematics, mathematical systems theory, and computer science makes

the study of discrete-event numerical methods particularly challenging. This chapter presents some basic

results, while avoiding more advanced topics. The goal is to present essential concepts clearly, and so

portions of this material will, no doubt, seem underdeveloped to a specialist. Pointers into the appropriate

literature are provided for readers who want a more in-depth treatment.

The remainder of this chapter is organized as follows. In Section 11.2, discrete-event simulation of

a single ordinary differential equation is introduced. This technique is expanded to systems of ordinary

differential equations in Section 11.3. A general scheme for representing discrete-event integration schemes

using the discrete-event system speciﬁcation (DEVS) is described in 11.4, and the ﬁrst-order method

introduced in Sections 11.2 and 11.3 are recast in terms of DEVS. In Sections 11.5 and 11.6, the ﬁrst-order

DEVS integrator is applied to simulating partial differential equations using ﬁnite differences in space and

discrete events in time. Second-order discrete-event integration schemes are discussed in Section 11.7. In

Section 11.8, the chapter concludes with a brief, but broad, overview of related research.

11.2 Simulating a Single Ordinary Differential Equation

Consider an ordinary differential equation that can be written in the form

˙x(t) = f (x(t)) (11.1)

Discrete-Event Simulation of Continuous Systems 11-3

Algorithm 11.1 Simulating a single ordinary differential equation.

t ←0

x ←x(0)

while terminating condition not met do

print t, x

if f (x) =0 then

h ←∞

else

h ←

|f (x)|

end if

if h =∞then

stop simulation

else

t ←t +h

x ←x +Dsgn( f (x))

end if

end while

A discrete-event approximation of this system can be obtained in, at least, two different ways. To begin,

consider the Taylor series expansion

x(t +h) = x(t) + h˙x(t) +

∞



n=2

(n)

(t) (11.2)

If we ﬁx the quantity D =|x(t +h) −x(t)|, then the time required for a change of size D to occur in x(t)

is approximately

h =



|˙x(t)|

if ˙x(t) = 0

∞ otherwise

(11.3)

This approximation drops the summation term in Eq. (11.2) and rearranges what is left to obtain h.

Algorithm 11.1 uses this approximation to simulate a system described by Eq. (11.1). The procedure

computes successive approximations to x(t) on a grid in the state space of the system. The resolution of

the state space grid is D, and h approximates the time at which the solution jumps from one state space

grid point to the next.

The sgn function, on line 14 in Algorithm 11.1, is deﬁned to be

sgn(q) =

⎧

⎨

⎩

−1ifq < 0

0ifq = 0

1ifq > 0

The expression Dsgn( f (x)) on line 14 could, in this instance, be replaced by hf(x) because

hf(x) =

|f (x)|

f (x) = Dsgn( f (x))

However, the expression Dsgn( f (x)) highlights the fact that the state space, and not the time domain, is

discrete. Note, in particular, that the computed values of x are restricted to x(0) +kD,wherek is an integer

and D is the state space grid resolution. In contrast, the computed values of t can take any value.

11-4 Handbook of Dynamic System Modeling

TABLE 11.1 Simulation of ˙x(t) =−x(t), x(0) = 1, Using

Algorithm 11.1 with D =0.15

txf(x) h

0.0 1.0 −1.0 0.15

0.15 0.85 −0.85 0.1765

0.3265 0.7 −0.7 0.2143

0.5408 0.55 −0.55 0.2727

0.8135 0.4 −0.4 0.3750

1.189 0.25 −0.25 0.6

1.789 0.1 −0.1 1.5

3.289 −0.05 0.05 3.0

6.289 0.1 −0.1 1.5

7.789 −0.05 0.05 3.0

0.2

0.4

0.6

0.8

012345678

x (t )

FIGURE 11.2 Computed solution of ˙x(t) =−x(t), x(0) =1 with D =0.15.

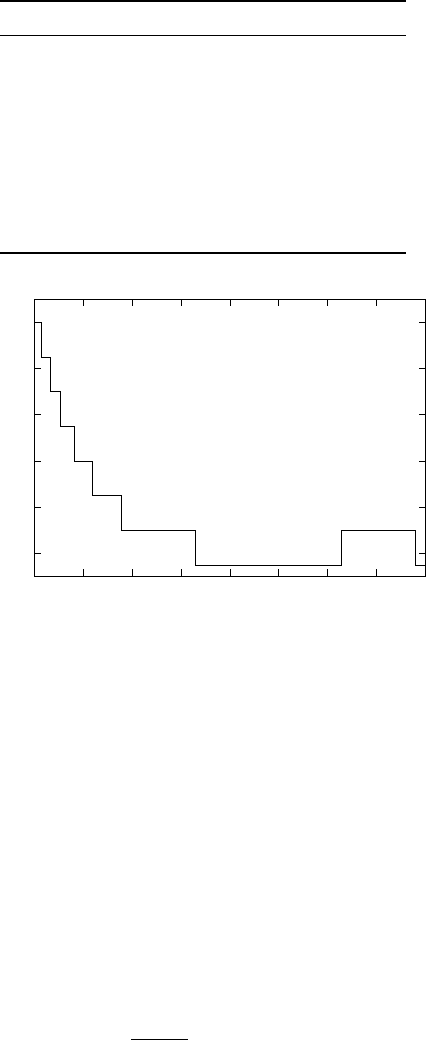
The procedure can be demonstrated with a simulation of the system ˙x(t) =−x(t), with x(0) =1 and

D =0.15. Each step of the simulation is shown in Table 11.1. Figure 11.2 shows the computed x(t)asa

function of t.

The approximation given by Eq. (11.3) can be obtained in a second way. Consider the integral





f (x(t))dt



= D (11.4)

As before, D is the resolution of the state space grid and h is the time required to move from one point

in the state space grid to the next. For time to move forward, it is required that h > 0. In the interval

, t

+h), the function f (x(t)) can be approximated by f (x(t

)). Substituting this approximation into

Eq. (11.4) and solving for h gives

h =



|f (x(t

))|

if f (x(t

)) = 0

∞ otherwise

This approach to obtaining h gives the same result as before.

There are two important questions that need answering before this can be considered a viable simulation

procedure. First, can the discretization parameter D be used to bound the error in the simulation? Second,

Discrete-Event Simulation of Continuous Systems 11-5

under what conditions is the simulation procedure stable? That is, under what circumstances can the error

at the end of an arbitrarily long simulation run be bounded? Several authors (see, e.g., Zeigler et al., 2000;

Kofman, 2004; Nutaro, 2003) have addressed these questions in a rigorous way. Happily, the answer to the

ﬁrst question is a“yes!” The second question, while answered satisfactorily for linear systems, remains (not

surprisingly) largely unresolved for nonlinear systems.

The ﬁrst question can be answered as follows: If ˙x(t) =f (x(t)) describes a stable and time-invariant

system (see Szidarovszky and Bahill [1998], or any other introductory systems textbook), then the error

at any point in a simulation run is proportional to D. The constant of proportionality is determined by

the system under consideration. The time-invariant caveat is needed to avoid a situation in which the ﬁrst

derivative can change independently of x(t) (i.e., the derivative is described by a function f (x(t), t), rather

than f (x(t))). In practice, this problem can often be overcome by treating the time-varying element of

f (x(t), t) as a quantized input to the integrator (see, e.g., Muzy et al., 2005).

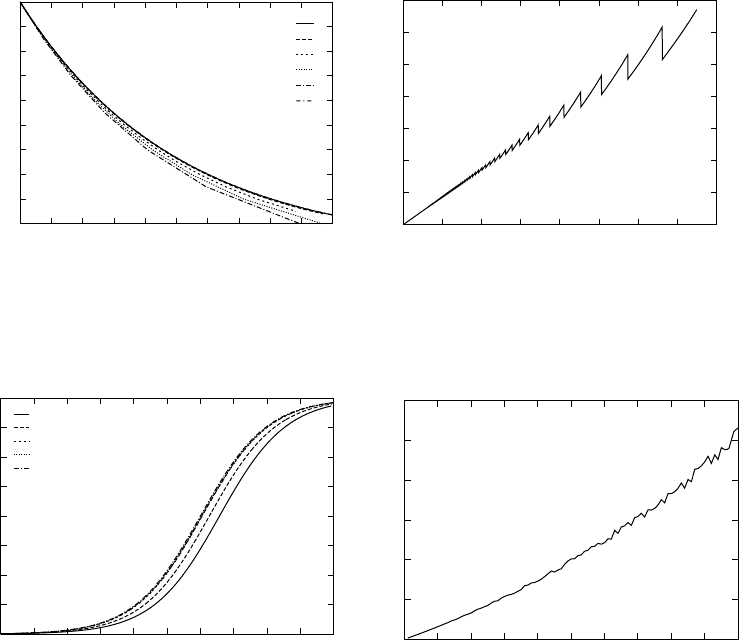
The linear dependence of the simulation error on D is demonstrated for two different systems in

Figure 11.3 and Figure 11.4. In these examples, x(t) is computed until the time of next event exceeds

a preset threshold. The error is determined at the last event time by taking the difference of the computed

and known solutions. This linear dependency is strongly related to the fact that the scheme is exact when

x(t) is a line, or, equivalently, when the system is described by ˙x(t) =k,wherek is a constant.

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

x (t )

D  0.001

D  0.01

D  0.05

D  0.1

D  0.15

exp(t )

(a)

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16

Absolute error

(b)

FIGURE 11.3 Error in the computed solution of ˙x(t) =−x(t), x(0) =1. (a) Comparison of computed and exact

solutions. (b) Absolute error as a function of D.

0.5

1.5

2.5

3.5

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

(

)

 0.01

 0.005

 0.001

 0.00075

0.02/(0.005(2.00.005)

exp(2

))

(a)

0.01

0.02

0.03

0.04

0.05

0.06

0 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 0.01

Absolute error

(b)

FIGURE 11.4 Error in the computed solution of ˙x(t) =(2 −0.5x(t))x(t), x(0) =0.01. (a) Comparison of computed

and exact solutions. (b) Absolute error as a function of D.

11-6 Handbook of Dynamic System Modeling

11.3 Simulating Coupled Ordinary Differential Equations

Algorithm 11.1 can be readily extended to sets of coupled ordinary differential equations. Consider a

system described in the following form:

¯x(t) =

f (¯x(t)) (11.5)

where ¯x(t)isthevector

(t), x

(t), ..., x

(t)]

and

f (¯x(t)) is a function vector

(¯x(t)), f

(¯x(t)), ..., f

(¯x(t))].

As before, we construct a grid in the m-dimensional state space. The grid points are regularly spaced by a

distance D along the state space axes. To simulate this system, four variables are needed for each x

, and so

4m variables in total. These variables are:

, the position of state variable i on its state space axis;

, the time until x

reaches its next discrete point on the ith state space axis;

, the last grid point occupied by the variable x

; and

, the last time at which the variable x

was modiﬁed.

The x

and y

are necessary because the function f

(·) is computed only at grid points in the discrete

state space. Because of this, the motion of the variable x

along its state space axis is described by a

piecewise constant velocity. This velocity is computed using the differential function f

(·) and the vector

¯y =[y

, ..., y

]. The value of y

is updated when x

reaches a state space grid point. The time required for

the variable x

to reach its next grid point is computed as

h =



D−|y

−x

(¯y)|

if f

(¯y) = 0

∞ otherwise

(11.6)

The quantity D is the distance separating grid points along the axis of motion, |x

−y

|the distance already

traveled along the axis, and f

(¯y) the velocity on the ith state space axis.

With Eq. (11.6), and an extra variable t to keep track of the simulation time, the behavior of a system

described by Eq. (11.5) can be computed with Algorithm 11.2.

To illustrate the algorithm, consider the coupled linear system

˙x

(t) =−x

(t) +0.5 x

(t) (11.7)

˙x

(t) =−0.1 x

(t)

with x

(0) =x

(0) =1 and D =0.1. Table 11.2 gives a step-by-step account of the ﬁrst ﬁve iterations

of Algorithm 11.2 applied to this system. The output values computed by the procedure are plotted in

Figure 11.5 (note that the ﬁgure shows the results beyond the iterations listed in the table). Each row in

the table shows the computed values at the end of an iteration (i.e., just prior to repeating the while loop).

Blank entries indicate that the variable value did not change in that iteration. The blank entries, and the

irregular time intervals that separate iterations, highlight the fact that this is a discrete-event simulation.

An event is the arrival of a state variable at its next grid point in the discrete state space. Clearly, not every

variable arrives at its next state space point at the same time, and so event scheduling provides a natural

way to think about the evolution of the system.

Stability and error properties in the case of coupled equations are more difﬁcult to reason about, but

they generally reﬂect the one-dimensional case. In particular, the simulation procedure is stable, in the

sense that the error can be bounded at the end of an arbitrarily long run, when it is applied to a stable

Discrete-Event Simulation of Continuous Systems 11-7

TABLE 11.2 Simulation of Two Coupled Ordinary Differential Equations on a Discrete State Space Grid

˙x

01−0.5 1 0 0.2 1 −0.1 1 0 1

0.2 0.9 −0.4 0.9 0.2 0.25

0.45 0.8 −0.3 0.8 0.45 0.3333

0.7833 0.7 −0.2 0.7 0.7833 0.5

1 0.6567 −0.25 1.0 0.2267 0.9 −0.09 0.9 1 1.111

Algorithm 11.2 Simulating a system of coupled ordinary differential equations.

t ←0

for all i ∈[0, m] do

←0

←x

(0)

←x

(0)

end for

while terminating condition not met do

print t, y

, ..., y

for all i ∈[0, m] do

←tL

,whereh

is given by Eq. (11.6)

end for

t ←min{tN

, tN

, ..., tN

}

Copy ¯y to a temporary vector ¯y

tmp

for all i ∈[0, m] such that tN

=t do

←x

(¯y

tmp

)

←y

←t

end for

for all j ∈[0, m] such that a changed y

alters the value of f

(¯y) and tN

=t do

←x

+(t −tL

(¯y

tmp

)

←t

end for

end while

0 5 10 15 20 25 30 35

0.2

0.4

0.6

0.8

y (t )

FIGURE 11.5 Plot of y(t) for the calculation shown in Table 11.2.