Fishwick P.A. (editor) Handbook of Dynamic System Modeling

Подождите немного. Документ загружается.

13-14 Handbook of Dynamic System Modeling

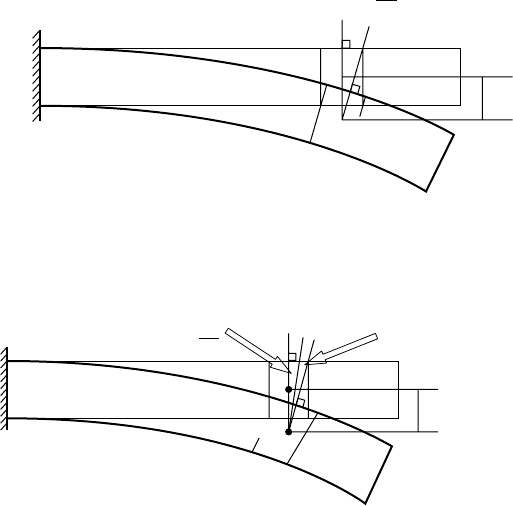
No shear—Normal remains normal to surface

u 

FIGURE 13.15 Kirchoff plate theory.

Shear included:

Rotation  Sum of dw/dx  Shear rotation

Shear deformation  θ

FIGURE 13.16 Mindlin plate theory.

of the derivative of w(x, y) and the shear deformation angle change. Figure 13.16 shows the relationship

between the displacement w(x, y), shear angle γ, and the derivative of the displacement.

This sum of angles to get the total rotation implies that independent shape functions can be used for the

displacement w and the rotations (

, 

). Mindlin theory is the most common formulation found in

ﬂat plate and shell elements used in current computer programs. This means there will not be rotational

continuity across elements boundaries (since shear exists). There is of course still rotational continuity at

the nodes. Hence the elements are considered to be C

elements.

In both the Kirchoff and Mindlin formulations, the pure plate bending element has three DOFs per node:

the normal displacement w and the out-of-plane rotations (

, 

). These are shown in Figure 13.17.

13.3.2 Generalized Stress

In plate theory, most derivations refer to the equations for generalized stress and strain. This is because the

equations for plate behavior can be converted to the form:

M(x, y) = E

∗

∗(curvature) (13.20)

where E

∗

is a modiﬁed constitutive matrix. Note that this is just like the equation for stress and strain

except we have moments replacing stresses and curvature replacing strain. In plates, the displacement

unknowns are the normal displacement and the two rotations. Following the analogy of generalized stress,

moments are equivalent to stress and curvature is equivalent to strain. This means that when using these

elements in modeling, we treat the moment gradient like we would stress to determine the level of shape

function and number of elements required for an accurate analysis. In addition, the difference in moment

at a common node between two elements indicates the adequacy of the mesh.

Finite Elements 13-15



and M

cause tension

in the z side of the plate

Plate DOF

Plate moment and stress results

FIGURE 13.17 Plate DOF and stress results.

The results from all plate elements consist of moments and the transverse shear, Q. It is important to

note that the moments and shear results are per unit length of plate.

Flat plate elements can be found in three- to nine-node versions, just like membrane elements. The

same concepts of shape function order are true for plates as they were for the membranes. Three-node

triangular plates model constant moments exactly. Nine-node elements model linear moments with some

second-order effects. It is important to remember that in plates, moments are equivalent to stress and

curvature is equivalent to strain, in terms of modeling. In other words, we need more elements in a high

moment gradient area for plates.

Flat shell elements combine the effects of plate bending with in-plane (membrane) effects. There

exist formulations for both ﬂat and curved shell elements. The curved element formulation is a more

complicatedderivation. The ﬂat shell howevercan be considered tobe merely the addition of the membrane

and ﬂat plate elements. This is the most common form of shell element found.

13.4 Solid Elements

The ﬁnal element we will look at is the 3-D solid element. This element is the most general of the ﬁnite

elements. It fully represents a 3-D stress and strain state. It is a fundamental building block that can be

used to create any shape structure. Clearly, as a structure becomes more complex, the effort required

deﬁning the geometry and mesh becomes time consuming. As a result of the required sophistication of

many analyses, many people are moving to computer-based solid geometry modeling of structures. This

especially includes mechanical components. Solid elements are a natural choice for this type of modeling

since any solid object can be meshed by solid elements.

13.4.1 Solid Element Behavior and DOF

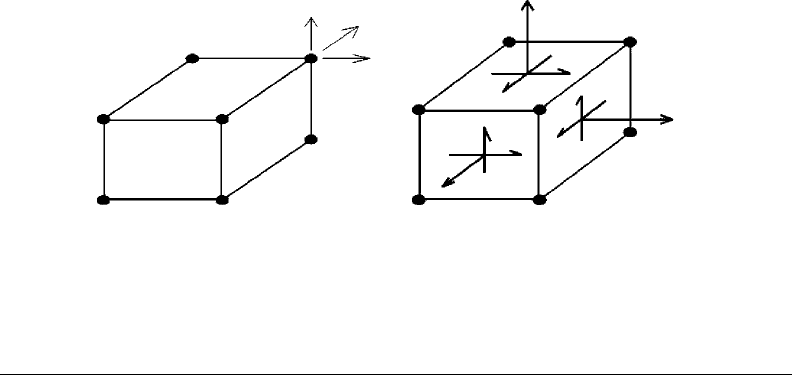
Solid elements are found in varied conﬁgurations analogous to membrane elements. They can be found in

four-node tetrahedrons, eight-node bricks, 20-node bricks, and 27-node bricks. Of course, variable node

versions exist that allow from 8 to 27 nodes.

The solid element is a 3-D analog of the membrane element. It has three DOFs per node. It does not

have any rotational DOF or rotational stiffness at the nodes. The solid element is capable of representing

a fully 3-D stress state. The available DOF and stress results for a typical eight node of a solid element are

shown in Figure 13.18.

The properties required for the solid element consist of Young’s modulus, E, and Poisson’s ratio, ν. Note

no thickness is required as was the case for membrane element. Solid elements model the full 3-D effects

of Hooke’s Law.

13-16 Handbook of Dynamic System Modeling

Solid element DOF Solid element stress results

FIGURE 13.18 3-D solid DOF and stress results.

13.5 Dynamics

In the displacement-based linear static ﬁnite element analysis method described above, the governing

equation to be solved is the static equilibrium equation:

Kq= F (13.21)

where K is the global stiffness matrix of the system, q a vector of global displacement DOF, and F avector

of global nodal forces (loads). Solving Eq. (13.21) yields a vector of spatially varying, but time-invariant,

displacements q that may be used to recover (back-calculate) element quantities such as strains, stresses,

and internal forces. Dynamic ﬁnite element analysis, in contrast, involves solution of a governing equation

of motion that is both spatially varying and time-varying:

M ¨q + C ˙q +Kq = F(t) (13.22)

In this equation, M is the global mass matrix of the ﬁnite element model under consideration, C the global

damping matrix, and K the global stiffness matrix. Quantities ¨q, ˙q, and q are vectors of time-varying nodal

accelerations, velocities, and displacements, respectively, and F(t) is a vector of time-varying forces acting

at the system DOF. The equation of motion can be interpreted as a force balance between inertial force M ¨q,

damping force C˙q, internal structural force Kq, and external load F(t). Dynamic ﬁnite element analysis

requires that the force balance described by Eq. (13.22) be satisﬁed at each point in time.

Formation of the global stiffness matrix K is carried out by assembling element stiffness matrices K

computed as indicated in Eq. (13.12), for all elements constituting the model. The global mass matrix M

is similarly constructed as an assembly of element mass matrices. A commonly used method of forming

element mass matrices M

isreferredtoastheconsistent-mass formulation and is given by



volume

ρ(H

∗H)δV (13.23)

where ρ is the mass density of the material and H a shape function matrix. Alternatively, in many

applications is it sufﬁciently accurate to simply lump mass at the nodes of the model in accordance with

tributary areas (or volumes) for each node. Such an approach produces a diagonal mass matrix and is

referredtoasalumped-mass formulation.

Methods of formulating the global damping matrix C are more varied than those used to form K and

M. Moreover, virtually all formulations of damping are simply mathematically convenient constructions

that only approximately represent actual damping phenomena that occur in solid materials. Dynamic

damping models are generally intended to model energy dissipation in structural materials. In Eq. (13.22),

Finite Elements 13-17

q(t)

F(t)

q(t)

F(t)

q(t)

F(t)

k, ck, c

FIGURE 13.19 Schematic diagrams of single degree of freedom (SDOF) systems.

a viscous damping model is employed in which the energy dissipating damping forces C ˙q are assumed

to be proportional to the nodal (particle) velocities ˙q. A common and mathematically convenient means

of formulating viscous damping matrices is referred to as Rayleigh damping (also called proportional

damping), and is given by

C = αM + βK (13.24)

where α and β are scalar constants. If the Rayleigh damping model is employed at the element level,

rather than at the global level indicated in Eq. (13.24), then element damping matrices are formed as

=αM

+βK

and are then assembled into a global damping matrix C in the same manner that element

mass and stiffness matrices M

and K

are assembled.

13.5.1 Single Degree of Freedom (SDOF) Dynamic Analysis

SDOF dynamic systems are structures in which inertial, damping, and stiffness (internal structural) forces

may be adequately described by a single displacement DOF q, and its time derivatives ˙q and ¨q. Schematic

diagrams of example SDOF systems are shown in Figure 13.19.

For an SDOF system, the equation of motion, previously described in terms of matrices and vectors in

Eq. (13.22), simpliﬁes to

m¨q + c ˙q +kq = f (t) (13.25)

where m, c, and k are scalar constants, and ¨q, ˙q, q, and f (t) are time-varying scalars. If no forcing (loading)

function f (t) is present, i.e., f (t) =0, then free vibration of the system results. Oscillation of a system

in free vibration may be initiated by nonzero initial conditions such as initial displacement and initial

velocity. In Figure 13.20, free vibration displacement responses q(t) for an undamped (c =0) system are

shown for cases of nonzero initial displacement q

=0, nonzero initial velocity ˙q

=0, and nonzero initial

displacement and velocity q

=0 and ˙q =0.

In each case shown in Figure 13.20, the SDOF system oscillates at the same characteristic frequency,

denoted the circular natural frequency of the system, and determined as

ω =



k/m (rad/s) (13.26)

Parameters related to ω are the natural frequency of the system f =ω/2π (Hz), and the natural period of

the system T =1/f (s). Because damping has been ignored in Figure 13.20, no dissipation of energy occurs,

and oscillation continues without decay. For damped cases in which c =0, energy dissipation during each

cycle of oscillation causes the amplitude of free vibration to decay. The rate at which this decay occurs is

a function of the level of damping c present in the structure. The level of damping may also be expressed

as a fraction of a special level of damping called critical damping. The critical viscous damping coefﬁcient

for an SDOF structure is given by

= 2mω = 2

√

mk (13.27)

13-18 Handbook of Dynamic System Modeling

Time, t

Displacement, q (t

)

Nonzero initial displacement, q

 0

Nonzero initial velocity, q

 0

Nonzero initial displacement and velocity, q

 0 and q

 0

FIGURE 13.20 Free vibration of an undamped SDOF system under nonzero initial conditions.

Critical damping c

is the minimum level of damping that will prevent oscillation of an SDOF dynamic

system in free vibration. For systems in which c < c

(underdamped), free vibration oscillations will

occur in response to nonzero initial conditions. However, for systems in which c > c

(overdamped), free

vibration oscillations will be completely suppressed. Damping levels in structures are therefore very often

described in relation to c

by using the parameter:

ξ = c/c

(13.28)

where ξ is called the ratio of critical damping or fraction of critical damping. Damping also generally affects

the frequency and period of oscillation. Analogous to the undamped natural circular frequency ω, the

damped circular frequency is deﬁned as

= ω



1 −ξ

(rad/s) (13.29)

Following from this deﬁnition, the damped frequency is f

=ω

/2π (Hz) and the damped period is

=1/f

(s). For most structural materials, natural damping levels fall within the range ξ<10%. For

such conditions, ω

∼

ω, f

∼

f , and T

∼

T. In Figure 13.21, displacement responses q(t) for undamped

and damped SDOF systems subjected to nonzero initial conditions are compared for various levels of

damping.

When a nonzero forcing function f (t) acts on a structure, the resulting response is referred to as forced

vibration. Depending on the complexity of f (t), one of a variety of different techniques may be employed

to quantify the displacement time-history of the SDOF system. For relatively simple mathematical forms

of f (t), Duhamel’s integral

q(t) = e

−ξωt



cos (ω

t) +

˙q

+ξωq

sin (ω



mω



f (τ)e

−ξω(t−τ)

sin (ω

(t −τ))dτ (13.30)

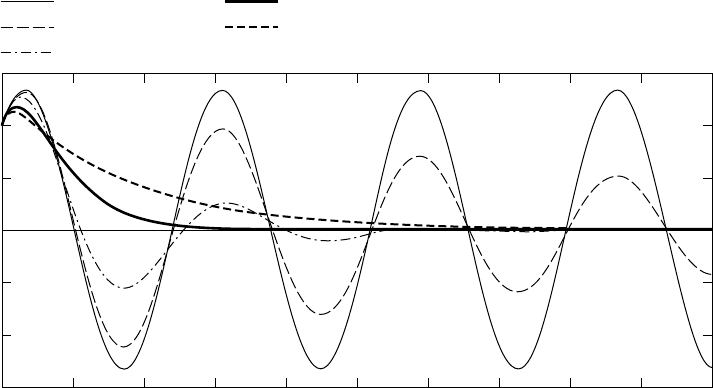
Finite Elements 13-19

Time, t

Displacement, q (t

)

ξ  0% (c  0)

ξ  5% (c  c

)

ξ  25% (c  c

)

z  100% (c  c

)

z  200% (c  c

)

FIGURE 13.21 Free vibration of a damped SDOF system under non-zero initial displacement and velocity conditions.

may be used to compute the displacement response q(t) of an SDOF system subjected to nonzero initial

conditions q

and ˙q

and forcing function f (t). For more complex forms of f (t)—as would arise, for

example, in seismic (earthquake) analysis—numerical methods must instead be employed. Generally,

direct integration techniques are used to time-integrate the equation of motion (Eq. [13.25]). All such

methods fall under the general classiﬁcation of time-domain analysis, because the equation of motion

is solved in the time-domain, advancing one time-step at a time through the entire range of times of

interest. Commonly employed direct integration methods include the average acceleration method, linear

acceleration method, and central difference method. For additional details regarding these numerical

procedures, the reader may consult Chopra (2000), Clough and Penzien (1993), Tedesco et al., (1999), and

Weaver and Johnston (1987).

13.5.2 Multiple Degree of Freedom (MDOF) Dynamic Analysis

In MDOF time-domain analysis, direct time-integration procedures may be applied either to the coupled

matrix equation of motion (Eq. [13.22]), or to a transformed form of that equation. For an MDOF

ﬁnite element model having n global DOFs, the matrices M, C, and K, in Eq. (13.22) will be n ×n in

size and nondiagonal (generally) in form. The presence of off-diagonal terms in these matrices couples

the various DOFs in the system together requiring that all n DOFs be time-integrated simultaneously.

A variety of numerical methods are available for direct time integration of MDOF-coupled equations of

motion. Examples include the average acceleration method, linear acceleration method, Wilson-θ method,

Newmark-β method, and the central difference method.

An alternative time-domain analysis approach for MDOF systems is to transform the n-dimensional

coupled equation of motion (Eq. [13.22]), into a set of n separate—and uncoupled—SDOF equations of

motion that can be solved individually using SDOF analysis methods. MDOF methods based on this type

of transformation are called modal methods because they generally employ normal (or natural) modes of

vibration in the transformation process. Normal modes of vibration, and the corresponding frequencies

at which these modes oscillate, are obtained by solving the eigen problem

Kφ = λMφ (13.31)

13-20 Handbook of Dynamic System Modeling

(t)

MDOF

structure

Mode 1

Eigen vector: f

Mode 2

Eigen vector: f

Mode 3

Eigen vector: f

FIGURE 13.22 Normal mode shapes (eigen vectors) for an MDOF system.

for the n eigen vectors φ and eigen values λ of the system. Normal mode shapes of the structure

(Figure 13.22) are described by the vectors φ whereas the corresponding frequencies are computed as

ω =

√

λ.

Normal modes of vibration exhibit a property called orthogonality, which is critically important in

transforming (uncoupling) the coupled equations of motion. For two normal modes r and s of a structure,

orthogonality with respect to the mass and stiffness matrices states that

Mφ

= 0 for r = s (13.32)

and

Kφ

= 0 for r = s (13.33)

If all n normal modes (eigen vectors) of a ﬁnite element model are collected into an eigen vector matrix

 =[φ

...φ

], the coupled matrix equation of motion Eq. (13.22) can then be transformed into

q +C

q +Kq = F(t) (13.34)

where

M =

M, C =

C, K =

K, and F(t) =

F(t). In Eq. (13.34), M, C, and K are the

modal mass, modal damping, and modal stiffness matrices, respectively; and

q, and q are the modal

accelerations, modal velocities, and modal displacements, respectively.

F(t) is the modal load vector. Each

of the modal matrices

M, C, and K is diagonal due to the orthogonality of the eigen vectors with respect

to mass and stiffness (C must be a Rayleigh damping matrix for

C to be diagonal). Because

C, and K

are diagonal, Eq. (13.34) then represents a set of n-separate, uncoupled SDOF modal equations of motion.

For a given mode r, the corresponding SDOF modal equation of motion is then

= f

(t) (13.35)

where

=φ

Mφ

, c

=φ

Cφ

, k

=φ

Kφ

, and f

(t) =φ

F(t). Each modal SDOF equation of motion

given by Eq. (13.35) may be solved using SDOF time-integration methods. Once all of the SDOF modal

equations of motion have been time-integrated to obtain time-histories of modal displacement

(t) for

each mode r, time-histories of structural displacements may be recovered by superposition

q(t) =



(t) (13.36)

In many practical applications of MDOF dynamic analysis, only a relatively small percentage of the n modes

of a system may participate substantially in dynamic response to loading. In such cases, the processes

Finite Elements 13-21

described above only need to be carried out for a truncated subset of p modes rather than making use

of all n modes. Under such conditions, modal analysis techniques may be more computationally efﬁcient

than methods that time-integrate the n-dimensional coupled equation of motion directly.

13.6 Summary

The basics of the ﬁnite element process have been described using the simple virtual work formulation and

physical elements as examples. There are numerous books and publications on ﬁnite elements that give

more detailed descriptions, alternate formulations, and speciﬁc formulations for different domains. What-

ever the domain or derivation method, the basics given in this chapter still hold and give the foundation

for understanding more complex modeling.

References

Bathe, K. J., 1995, Finite Element Procedures, New Jersey, Prentice-Hall.

Chopra, A., 2000, Dynamics of Structures: Theory and Applications to EarthquakeEngineering (2nd Edition),

New Jersey, Prentice-Hall.

Clough, R. W. and Penzien, J., 1993, Dynamics of Structures, New York, McGraw-Hill.

McGuire, W., Gallagher, R., and Ziemian, R., 2002, Matrix Structural Analysis, MATSTAN 2 V2.0

(2nd Edition), New Jersey, Wiley.

Tedesco, J. W., McDougal, W. G., and Ross, C. A., 1999, Structural Dynamics: Theory and Applications,

Reading, MA, Addison-Wesley.

Weaver, W. and Johnston, P. R., 1987, Structural Dynamics by Finite Elements, Prentice-Hall.

Zienkiewicz, O. C. and Taylor R. L., 2000, Finite ElementMethod: Volume 1, The Basis, Oxford, Butterworth-

Heinemann.

Zienkiewicz, O. C., 2000, Finite Element Method: Volume 2, Solid Mechanics, Oxford, Butterworth-

Heinemann.

Zienkiewicz, O. C. and Taylor R. L., 2000, Finite Element Method: Volume 3, Fluid Dynamics, Oxford,

Butterworth-Heinemann.

Multimodeling

Minho Park

Stephen F. Austin State University

Paul A. Fishwick

University of Florida

Jinho Lee

Samsung Electronics

14.1 Introduction ................................................................ 14-1

Integrative Multimodeling

•

General Multimodeling

•

RUBE Framework

14.2 Scene Construction ..................................................... 14-5

Ontology

•

Interaction Model Creation

•

Blender Interface

14.3 Multimodeling Exchange Language (MXL) .............. 14-11

Concepts of MXL

•

Multimodeling in MXL

14.4 Dynamic Exchange Language (DXL) ......................... 14-13

DXL Concepts

•

Syntax of DXL

•

Semantics of DXL

•

Multimodeling

14.5 A Boiling Water Example ............................................ 14-20

2D Representation

•

Model Creation

•

Code Generation

14.6 Conclusion .................................................................. 14-27

14.1 Introduction

Multimodels are models that are composed of other models either through homogeneous or heterogeneous

coupling. Multimodeling (Fishwick, 1995) is the process of engineering a model by combining different

model types to form an abstraction network or hierarchy. Multimodeling, in a nutshell, endows the

simulation modeler with the capability to blend different model types together to form hybrid models.

When we begin to understand a physical system by creating a model, we often ﬁnd that the model is too

limited: the model will answer only a very limited set of questions about system behavior. It is necessary,

then, to create many models and link them, thereby maintaining a multilevel view of a system while

permitting an analyst to observe system output at several abstraction levels. For example, consider this

scenario: a region withseveral key military vehicles and targets, planes (both ﬁghter as well as command and

control center), surface-to-air missile (SAM) sites, and drones. A variety of models deﬁne the geometry and

dynamics of these objects. Ideally, we can explore and execute these models within a 2D or 3D visualization

environment by formalizing domain knowledge and providing a well-deﬁned modeling methodology.

We will introduce two multimodeling approaches, integrative multimodeling (Fishwick, 2004; Park

and Fishwick, 2004a, 2004b; Park, 2005) and general multimodeling (Fishwick, 1995; Lee, 2005). The

purpose of integrative multimodeling is to provide a human–computer interaction environment that

allows components of different model types to be linked to one another—speciﬁcally dynamic models

used in simulation to geometry models for the phenomena being modeled. General multimodeling,

however, describes a number of abstraction perspectives for a complex real-world system using simulation

model types such as ﬁnite state model (FSM) and functional block model (FBM) (Fishwick, 1995).

To support the above multimodeling environments, we developed an XML-based modeling and simu-

lation framework called RUBE (Kim et al., 2002; Kim and Fishwick, 2002a, 2002b; Fishwick, et al., 2003;

Fishwick, 2002), which encompasses the modeling process of a real-world system as well as the simulation

14-1