Fishwick P.A. (editor) Handbook of Dynamic System Modeling

Подождите немного. Документ загружается.

15-14 Handbook of Dynamic System Modeling

TABLE 15.1 Event Calendar

Time (ms) Event

20 open_tonneau

2020 move_top_up_cmd

2150 move_down_window

2250 stop_moving_window

For aperiodic events, this approach may not be applicable, as the accuracy with which the time at which

events can be effected degenerates to the period of the base rate, which is typically too coarse.

In case state events are present, a numerical solver with zero-crossing detection built-in is desirable. Such

a numerical solver returns before the ﬁnal time is reached and reports the time at which a zero crossing

was found.

15.4.4 Event-Driven Execution

Another approach to generating behavior takes an event-driven perspective. This is particularly efﬁcient

for time events that are aperiodic and often have a stochastic component to their time of occurrence.

Rather than having a numerical solver move time forward until each of the events occurs, time imme-

diately jumps from one event time to another. To efﬁciently implement this, typically an event calendar is

used to keep track of all events that are scheduled to occur. An example of an event calendar is presented in

Table 15.1. It shows how the ﬁrst upcoming event to occur is at 20 (ms), followed by another at 2020 (ms).

An event-driven approach is much more efﬁcient in handling aperiodic time events as it does not

require a time-driven solver to move time forward by means of integration over time. Typically, hundreds

of thousands of events can be conveniently simulated in a matter of seconds.

To achieve such efﬁciency, it is critical that the event calendar be implemented in an efﬁcient manner. In

particular, efﬁcient search of the event calendar needs to be facilitated, because new events must be inserted

in the correct place, and events that were scheduled at one time may have to be located and retracted at a

later time.

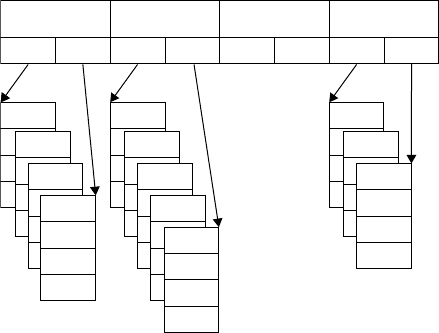
One implementation, called calendar queue, mimics a traditional calendar [3], which uses an array to

index into a number of bins while the content of each bin is implemented as a doubly linked list. In this

list, each item has a link to the next item as well as the previous item, which allows each item in the list

to be accessed in a forward as well as backward manner. Deleting any item can then be done in constant

time. The array that implements the number of bins has constant access time to each of the bins.

This is illustrated in Figure 15.11 where four bins are represented by the array at the top. The bin with

index 0 contains all elements with a time stamp in the range from 0 to 1, with 1 not included; the bin with

index 1 contains all elements with a time stamp in the range from 1 to 2, with 2 not included, etc. Events

with a time stamp of 4 or more are distributed based on the result of the time stamp modulo 4.

The calendar queue combines the beneﬁt of quick insertion of events in the doubly linked list where the

array is more efﬁcient for indexing a large event calendar. Further permutations of different data structures

such as arrays, lists, and heaps can be devised depending on the characteristics of the event distributions

particular to a problem under study. For example, if the number of scheduled events varies greatly during

simulation, dynamically reconﬁguring the data structure may become important.

Note that an event-driven implementation can be exploited to generate behaviors for continuous-time

models as well. In this approach, the numerical solver is modeled as a discrete-event component and the

computations at each time step are aperiodic events to be handled (e.g., D’Abren and Wainer, 2003).

15.4.5 Combining the Execution Types

In many applications of modeling and simulation, in particular for hybrid dynamic systems, it is common

to have an extensive model component that is of an aperiodic discrete-event nature as well as a component

that is of a continuous-time nature. For example, the power window system in Figure 15.3 may contain

Hybrid Dynamic Systems: Modeling and Execution 15-15

Lead Lead Lead LeadTail Tail Tail Tail

0.1

data

1.5

data

0.4 1.6

next next

data data

prev prev

0.5 5.1

next next

data data

prev prev

4.2 5.8

Data

data

3.3

data

3.4

data

19.5

Data

9.3

Data

0123

FIGURE 15.11 Calendar queue event list.

a detailed continuous-time model of the door with window, dc motor actuator, signal conditioning

hardware, and the like, all of which may contain some discontinuitiesmodeledby local ﬁnite state machines.

Similarly, the controller may operate in a discrete-time manner because it executes with a given sample

rate. The controller may implement an extensive signal processing component, data analysis computations,

supervisory control, and further elements. The CAN behavior may be modeled in detail by a discrete-

event model that performs behaviors such as capturing the generation of packets, routing them through

the network, and possibly resending dropped packets.

To efﬁciently execute models that comprise all of these behaviors, it is desirable to support: (i) a

numerical solver for continuous-time behavior, (ii) a scheduler for the discrete-time behavior, and (iii) an

event calendar handler for the discrete-event behavior.

Because of the predictability of the discrete-time events and the ﬁxed base rate, discrete-time behavior

as handled by a scheduler can often be conveniently integrated into the numerical solver to comprise a

time-driven execution engine. A getNextEventTime call is typically exploited to tell the solver the time until

which it should solve for the continuous-time behavior.

The discrete-event part is a different matter, though. Because there is no ﬁxed base rate, events may

occur arbitrarily close in time. Halting the numerical solver at each of these points in time quickly becomes

very inefﬁcient. So an event-driven execution engine is preferred.

Rather than integrating the time-driven execution engine that uses a numerical solver and event schedule

with the event-driven execution engine that relies on an event calendar, it is more efﬁcient to combine the

two different execution engines. When combining the two, it is important to ﬁrst observe that the event-

driven engine may process many events that have no bearing on the time-driven behavior. The time-

and event-driven execution engine can then compute behavior independently until an event is generated

that requires interaction between the two. This requires coordination between the time- and event-driven

execution to ensure the two are synchronized upon communication (Nicolescu et al., 2006).

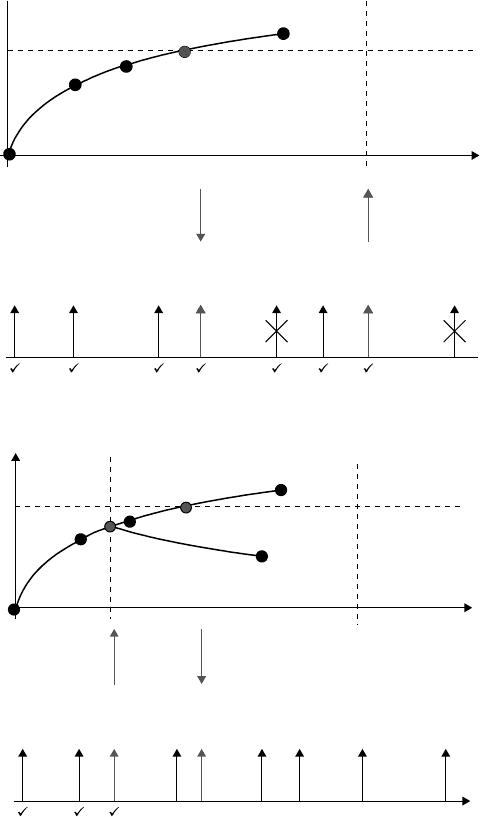
Two possibilities to implement this are illustrated in Figure 15.12. In Figure 15.12(a), the event-driven

behavior shown at the bottom leads the time-driven behavior shown at the top. Behavior generation starts

with processing the events (indicated as vertical arrows) that are registered on the event calendar. When

the ﬁrst event that has a bearing on the time-driven behavior is processed, a time event is set and the

numerical solver starts integrating up to that point in time, shown at the top. A complication arises when

the continuous-time behavior exceeds a threshold that causes a state event to occur that has a bearing on

the event-driven behavior located in time before the time event that was set. This state event then occurs at

a point in time that the event-driven execution has passed already. So, events that were already processed

have to be retracted and the state of the event-driven behavior has to roll back.

15-16 Handbook of Dynamic System Modeling

The other possibility is illustrated in Figure 15.12(b), where the time-driven behavior leads the event-

driven behavior. In this case, the state event is generated and registered on the event calendar before the

event-driven behavior reaches this point in time and execution control is handed over to the event-driven

behavior to catch up. Now, it may happen that the event-driven behavior sets a time event in the time-

driven execution at a point in time before the state event occurred. This event may cause a change in

continuous-time behavior, and the threshold that caused the state event may never be reached. So, the

time-driven execution engine needs to roll back.

Efﬁcient implementations can be developed based on, for example, employing an interpolation polyno-

mial in the time-driven part to quickly obtain the previous continuous-time state values, so the numerical

integration does not have to be restarted anew, which is an expensive proposition.

Registered

events

Processed

events

Continuous

time

time event

This event

never occurs,

but it is

already

processed!

This sets a

time event

in the

time-driven

solver

This sets an

event in the

event-driven

solver

state even

(a)

Registered

events

Processed

events

Continuous

time

state even

time event

This sets an

event in the

event-driven

solver

This sets a

time event

in the

time-driven

solver

This event never occurs,

but it is already

processed

(b)

FIGURE 15.12 Combining event-driven and time-driven execution. (a) Event-driven leads and (b) time-driven leads.

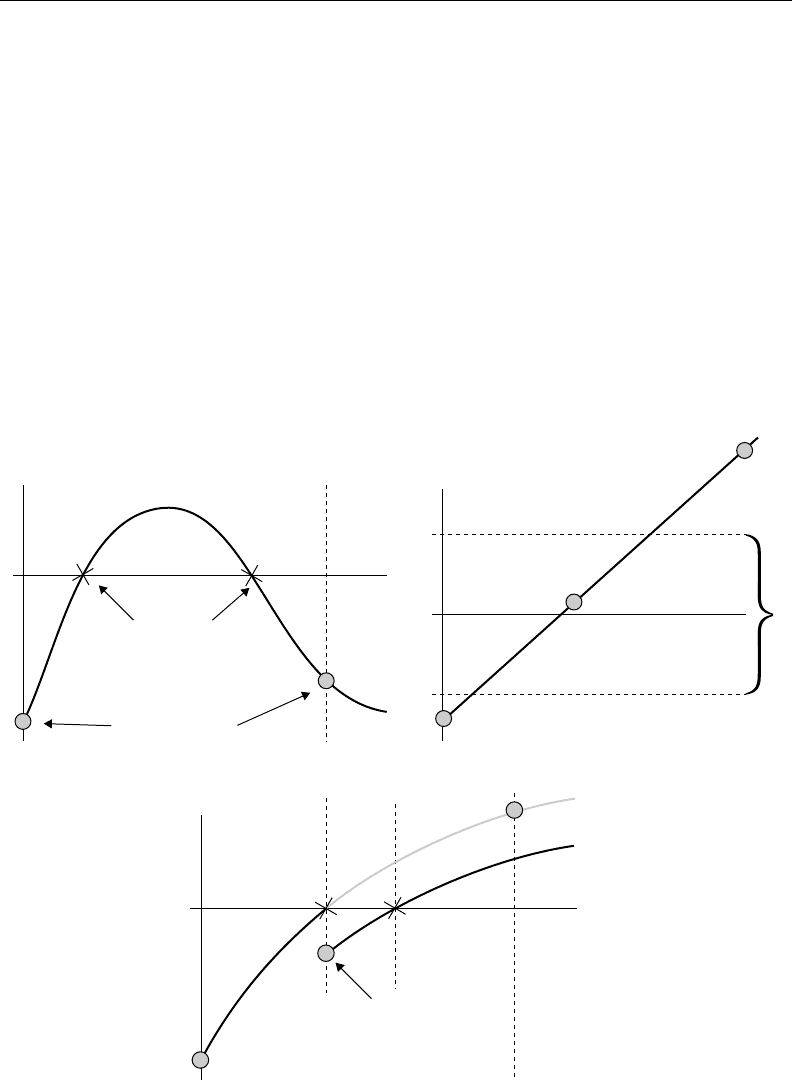
Hybrid Dynamic Systems: Modeling and Execution 15-17

15.5 Advanced Topics in Hybrid Dynamic System Simulation

To build on the understanding of the basic elements of a hybrid system, some of the complications that

arise when implementing and combining these elements are explored.

15.5.1 Zero-Crossing Detection

The typical approach to zero-crossing detection compares the sign of a function result and if it changes, it

has crossed zero. This approach may fail if the zero-crossing function has an even number of zeros in the

interval T between the two evaluated points as determined by the numerical integration algorithm. This

is illustrated in Figure 15.13(a). In general, the zero-crossing function, z, is a function of the model state,

but it does not contribute to its continuous dynamics, f . Therefore, numerical integration can proceed

without taking the dynamics of z into account, and when these are faster than the dynamics of f , the

situation with even zeros may arise.

One solution to the even zeros problem is to include the dynamics of z in the model dynamics so the

numerical solver adjusts its step size when too large an error in the zero-crossing function dynamics is

found (Park and Barton, 1996). This does not, however, address the problem of moving outside of the

domain of the zero-crossing function, such as outlined for the square root computation in Section 15.3.3.

Zero crossing

Integration points

(a)

Numerical 0





(b)

Reinitialization

(c)

FIGURE 15.13 Difﬁculty in zero-crossing detection and location. (a) Even roots, (b) comparing a ﬂoat, and

15-18 Handbook of Dynamic System Modeling

To avoid moving outside of a function domain, an alternate approach to event detection relies on a

feedback-control concept. If k is the index of the points in time at which the numerical solver computes

a value, t

, then, if k is considered dense rather than discrete, the step size between consecutive points, h,

becomes h(k) =

. This step size can be chosen as

h(k) =−η

z(x)

∂z

∂x

(15.14)

to control the step size selection (Esposito et al., 2001). Given the sensitivity of the zero-crossing function,

z, with respect to the step size



∂z

∂x





∂z

∂x



h(k) (15.15)

this results in z behaving as

=−ηz (15.16)

which gradually converges to 0 without actually crossing it. Instead, the solution to Eq. (15.16) is

z(k) =z(0)e

−ηk

, and z(k) approaches 0 exponentially as k tends to inﬁnity. So, the function domain is

never departed. However, this requires a number of additional computations during numerical integration

such as the sensitivity, and, therefore, is computationally less attractive.

Other than exceeding the threshold value, another issue with zero-crossing detection arises when the

zero-crossing function z returns 0 exactly. This does not constitute a crossing, and, therefore, is not detected

as such. Root-ﬁnding facilities of numerical solvers may require the function z to actually change sign

between two integration steps to report that a crossing has occurred. For example, when z starts off at

0 and then moves away from it, no zero-crossing event would be generated and consequently no mode

change could occur.

One solution is the use of a zero-crossing function that is not at 0 exactly. Rather, it is chosen to be

− when z is negative and  when z is positive, with  very small. When −<z <, both zero-crossing

functions, z − and z +, are used.

One effect of this implementation is the need for a “numerical 0”; a ± band around 0 in which the

zero-crossing function is considered to be the 0 value of the sign function.

sign(x) =

⎧

⎨

⎩

−∀

(x < −)

0 ∀

(− ≤ x ≤ )

+∀

(x >)

(15.17)

As long as the zero-crossing function evaluates to a value within the ± band, its sign is considered to be 0.

This approach has an important implication for the analytical correctness of comparing for equality.

If a simulation contains the comparison with zero, x =0, when x is a continuous signal, a zero-crossing

function z(x, u, t) is used to ﬁnd the value of x that satisﬁes this equality within a certain tolerance. For

this value, x



, the zero-crossing function has sign 0, whereas the strict equality x =0 may not be satisﬁed.

Figure 15.13(b) shows how the signal x may therefore cross 0 without having x =0 evaluate to true because

the analytical solution that satisﬁes this comparison is never evaluated by the numerical integration.

Another issue that is less critical but still causes inefﬁciencies to occur because of recomputation of the

model variables after the zero crossing has been located. Because of numerical inaccuracies, even if no

changes to the states are made that are used to compute a zero-crossing variable, the return value of the

function may still differ. This is illustrated in Figure 15.13(c), which shows that restarting the simulation

results in a function return value that is slightly different from the computed value immediately before

the zero crossing. Continuing simulation leads to the same zero crossing being detected and located again.

This phenomenon has been referred to as discontinuity sticking (Park and Barton, 1996).

Hybrid Dynamic Systems: Modeling and Execution 15-19

15.5.2 Mode Changes

When a change between modes occurs, the continuous-time state variables may have to be reinitialized

and an immediate consecutive mode change may occur as a result.

15.5.2.1 Reinitialization

An important phenomenon of the general DAE form 0 =f

(˙x, x, u, t) is that the system may only be allowed

to move in part of the generalized state space (Verghese et al., 1981). This is the case, for example, when

the power window in Figure 15.2 collides with an object, m

object

, in a perfectly nonelastic manner. After

the collision, the window and object proceed to move with equal velocity, and this leads to the equations

object

˙v

object

window

˙v

window

lift

window

= ru

motor

object

= v

window

˙x

window

= v

window

˙x

object

= v

object

(15.18)

to describe the dynamic behavior. In the form of a matrix pencil (Demmel and Kägström, 1986) with a

forcing function, E ˙x +Ax +Bu =0, this becomes

⎡

⎢

⎣

window

object

0000

0010

0001

⎤

⎥

⎦

⎡

⎢

⎣

˙v

window

˙v

object

˙x

window

˙x

object

⎤

⎥

⎦

⎡

⎢

⎣

lift

000

−1100

−1000

0 −100

⎤

⎥

⎦

⎡

⎢

⎣

window

object

window

object

⎤

⎥

⎦

⎡

⎢

⎣

−r

⎤

⎥

⎦

[

motor

] = 0

(15.19)

Here, because of the constraint that v

window

object

, only the part of the state space for which this

constraint holds can be accessed. This implies that there is also a limitation on the reachability in the

window

, x

object

space, but this is a nonholonomic constraint rather than it being disallowed.

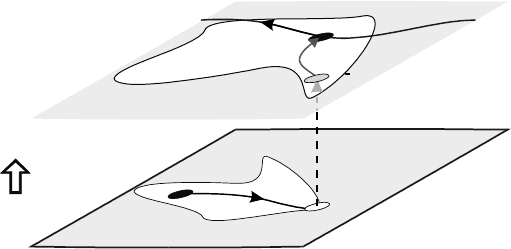
In a generalsense, the reducedstate space can be representedin geometricterms as shown in Figure 15.14.

Here, the system evolves in a mode α

until the boundary of a patch is reached. At this point in time, the

system transitions into another mode, but the continuous-time state is not in the allowed space, which is

marked by the thick solid line. To arrive at a consistent situation, the continuous-time state has to be in

the allowed space, and the exact value is computed based on the jump space, which is the space in which

the required instantaneous changes are allowed.

In the linear case, this computation in the jump space corresponds to a projection. This projection can be

computed in several ways (Gantmacher, 1965; Griepentrog and März, 1986; Lewis, 1992; Mosterman, 2000,

2002; van der Schaft and Schumacher, 1996; Verghese et al., 1981). To illustrate the method in Mosterman

(2001), the Weierstrass normal form is derived for the velocity part of the equations in Eq. (15.19). The







FIGURE 15.14 A projection. (From Mosterman, P. J. Mode transition behavior in hybrid dynamic systems. In

Proceedings of the 2003 Winter Simulation Conference, pp. 623–631, New Orleans, LA, December 2003 (invited paper).)

15-20 Handbook of Dynamic System Modeling

positions are geometric states that do not change discontinuously, and, therefore, are irrelevant for the

example. This leads to the system of equations



window

object



˙v

window

˙v

object





lift

−11



window

object





−r



[

motor

] = 0 (15.20)

After applying the following change of basis:



window

object





1 −

object

window



−

window

+ m

object





¯v

window

¯v

object



(15.21)

the following matrix pencil is arrived at:



window



¯v

window

¯v

object



⎡

⎣

window

+ m

object

lift

window

+ m

object

window

⎤

⎦



¯v

window

¯v

object





−r



[

motor

] = 0 (15.22)

The matrix



window



contains a ﬁnite space (top-left entry) [m

window

] and inﬁnite space (bottom-

right entry) [0]. Note that this is an index 1 system of equations, as the inﬁnite space is the null matrix.

Therefore, its nilpotency is 1, and this is also referred to as the index of the system of equations (van

Dijk, 1994). The nilpotency is an indicator of how many stages of substitution are required to compute

all inﬁnite variables. Eq. (15.22) is considered to be of index 1 because the inﬁnite variable, ¯v

object

, can be

computed in one stage, i.e., ¯v

object

=0.

The ﬁnite part in Eq. (15.22) consists of ¯v

window

and this can be converted into a regular one-dimensional

ODE by inverting the matrix [m

window

] and left-multiplying. Because it is a regular ODE, there is no

discontinuous change in the variable ¯v

window

,or

¯v

window

=¯v

−

window

(15.23)

where the “−” superscript indicates the ﬁnal value of ¯v

window

before the mode change (in case of the

initialization before simulation starts, it is the user-supplied initial value).

Now, from v

−

window

and v

−

object

, the value ¯v

−

window

can be computed using the inverse change of basis.

Straightforward computations yield

¯v

−

window

= v

−

window

object

window

−

object

(15.24)

which equals ¯v

window

. With ¯v

object

=0 the change of basis can now be applied to yield

window

object

window

−

window

object

−

object

) (15.25)

and from v

window

object

, v

object

can be computed. Details on the derivation are available in previous

work (Mosterman, 2000).

15.5.2.2 Sequences of Mode Changes

After one mode change, γ

i+1

, and computing the initial values of the continuous-state variables in the

new mode, a new transition, γ

i+2

i+1

, may follow immediately as shown in Figure 15.9 (Mosterman and

Biswas, 1996). The mode change causes a new mode to be arrived at, after which reinitialization is per-

formed again. This process repeats until no further mode changes occur and the system proceeds to evolve

continuously again.

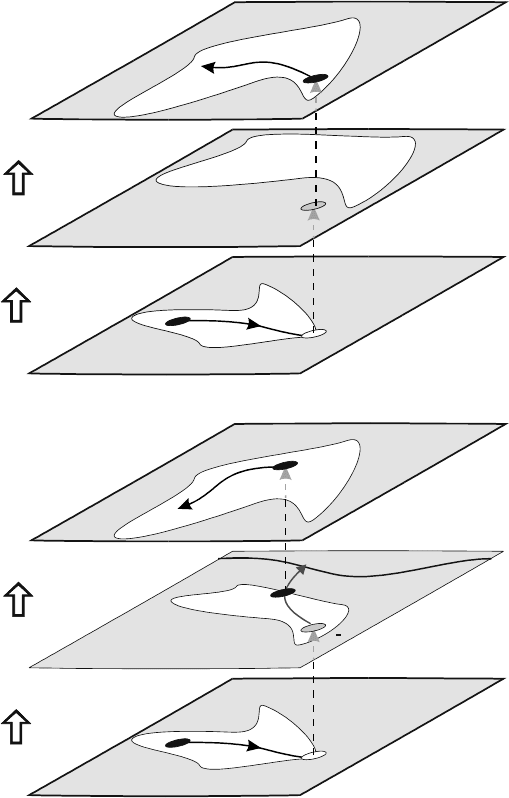
Hybrid Dynamic Systems: Modeling and Execution 15-21

The values of the continuous-time state in modes where there is no continuous-time behavior can be

of two types (Mosterman and Biswas, 1996):

•

When the value does not change from the previous mode, and the mode is a so-called mythical

mode (Figure 15.15(a)).

•

When the reinitialization causes a change in value from the previous mode, which results in an

isolated point, a so-called pinnacle, with no continuous behavior in that mode (Figure 15.15(b)).

In case of sequences of mode transitions, the left-closedness mentioned in Section 15.3.3 may (have to)

be relaxed, though, in particular for sequences of pinnacles. For example, a pressure relief valve may move

through a sequence of opening and closing cycles before the pressure has subsided to below the threshold

for opening the relief valve. In a sufﬁciently detailed model, this sequence occurs over time, but when small



(a)









(b)









FIGURE 15.15 Sequences of mode transitions. (a) State invariance and (b) state reinitialization. (From

Mosterman, P. J. Mode transition behavior in hybrid dynamic systems. In Proceedings of the 2003 Winter Simulation

Conference, pp. 623–631, New Orleans, LA, December 2003 (invited paper).)

15-22 Handbook of Dynamic System Modeling

physical phenomena are not included in the model, for example, to simulate it in real time, this sequence

may occur at one point in time (Mosterman, 2002). Note that this requires the “state” of the system to

include an additional dimension to allow multiple values at one point in time. This can be done by using

pairs that consist of the continuous-time state and an index (Guckenheimer and Johnson, 1995).

An important behavior that is not properly dealt with in simulation tools at present is the crossing of

the patch boundary in an intermediate mode such as in mode α

in Figure 15.15(b). The proper value

of the continuous state to be applied for initialization in mode α

appears to be the point at which the

projection crosses the patch boundary. However, there may be physical phenomena that are best modeled

with a different semantics. This is still a subject of research.

15.6 Pathological Behavior Classes

Once sequences of mode changes occur, models can be constructed that contain loops of mode changes,

i.e., a previously visited mode is revisited, without continuous-time behavior evolving in between.

Two classes of behavior are illustrated in Figure 15.16. In Figure 15.16(a), the pathological case is shown

that violates the divergence of time principle (Mosterman and Biswas, 1998). Here, the state is initialized

inside of the patch in mode α

. It evolves continuously until it reaches the patch boundary as deﬁned by

. When the state x

is then transferred to mode α

, it is outside of the patch as deﬁned by γ

(note

the exchange in subscripts of α). This causes the state to be transferred back to α

where it is outside of

the patch as deﬁned by γ

. Thus, a loop of discrete changes between modes arises.

Because these are

instantaneous, no time elapses, and, therefore, the model stops evolving in time. In other words, time does

not diverge. Since this behavior is not observed in physical systems, such behavior is considered the result

of anomalous models of physics.

Similar but different behavior is illustrated in Figure 15.16(b). Here, after reaching the patch boundary

in α

, the state transfers onto the patch boundary in α

as deﬁned by γ

(note again the exchange in

subscripts of α). Because it is the patch boundary, the state transfers back to α

after an inﬁnitesimal step

in time. This step results in a value x

that may be immediately inside the patch in α

as deﬁned by γ

and so another inﬁnitesimal step will transfer the state back to α

Far-fetched and pathological as it may seem, this behavior, referred to as chattering or sliding mode

behavior, is actually aimed for by robust control design methodologies (Utkin, 1992) (e.g., it is used in

antilock braking systems), as it is relatively insensitive to plant model parameter variations. Unlike the

behavior in Figure 15.16(a), here the state does continue to evolve in time and the divergence of time

principle is satisﬁed. To efﬁciently derive the actual behavior along the switching surface as deﬁned by the

patches in mode α

and α

, two methods can be applied: (i) equivalence of control (Utkin, 1992) and

(ii) equivalence of dynamics (Filippov, 1960; Mosterman et al., 1999). Although there are classes of models

for which these “regularizations” result in the same behavior, in general they may differ.

Finally, another class of pathological behaviors can be identiﬁed, namely Zeno behavior.

Behaviors that

are Zeno do progress in time by a noninﬁnitesimal value each time a mode transition occurs. However,

this time reduces upon each transition as a converging series. For example, in case the time is halved upon

each transition, the transition series converges to a limit value in time

= 

(15.26)

that is never exceeded. In case the bounce-back of the window in the hybrid automaton in Figure 15.8(b)

does not include the threshold clause, the bounce transition would be taken indeﬁnitely, with shorter

Note that a loop may involve any ﬁnite number of modes.

Note how left-closedness is violated in this particular instance of behavior. In general, an inﬁnitesimal “hysteresis”

effect may be present to guarantee left-closedness again.

Named after the Greek philosopher Zeno who studied the relation between points and intervals, i.e., whether an

interval is an inﬁnite collection of points.

Hybrid Dynamic Systems: Modeling and Execution 15-23



(a)









(b)









FIGURE 15.16 Recurring mode transitions. (a) Nondivergent and (b) sliding. (From Mosterman, P. J. Mode transi-

tion behavior in hybrid dynamic systems. In Proceedings of the 2003 Winter Simulation Conference, pp. 623–631, New

Orleans, LA December 2003 (invited paper).)

and shorter intervals of time in between. Depending on the coefﬁcient of restitution, η, the new interval

between bounces would be a fraction of the present one. The increasingly smaller intervals would converge

to a limit point in time beyond which time would not progress. Therefore, although time diverges locally,

it does not do so globally.

It is now possible to compare the three mode revisiting behaviors.

•

Divergence of time: inﬁnitely many discrete steps in zero time. Time remains the same.

•

Chattering: inﬁnitely small time steps. Evolves past any value in time.

•

Zeno: inﬁnitely many time steps in a ﬁnite, nonzero, time interval. Does not evolve past a limit point

in time.

Note that, although it is important to clearly distinguish between these three behaviors, often Zeno is used

as an all-encompassing term that includes each of these (e.g., behavior that is locally not divergent in time

is often called Zeno as well).

15.7 Conclusions

This chapter presented an overview of the ﬁeld of numerical simulation for hybrid dynamic systems. It

discussed the basic parts of continuous-time behavior generation, event detection and location, mode

transitions, and reinitialization that are needed and how they combine together.

The implementation was shown to be potentially based on a numerical integrator scheme, use of a

statically compiled schedule, and use of a dynamically kept event calendar. In some cases, it may be