Fisher John P. e.a. (ed.) Tissue Engineering

Подождите немного. Документ загружается.

mikos: “9026_c006” — 2007/4/9 — 15:50 — page 20 — #20

6-20 Tissue Engineering

[151] Noble, P.B., Boyarsky, A., and Bentley, K.C., Human lymphocyte migration in vitro: charac-

terization and quantitation of locomotory parameters. Can. J. Physiol. Pharmacol., 1979, 57:

108–112.

[152] Papoulis, A., Probability, Random Variables and Stochastic Processes. New York, NY: McGraw-Hill,

pp. 532–551, 1965.

[153] Ratcliffe, A. and Niklason, L.E., Bioreactors and bioprocessing for tissue engineering. Ann. NY

Acad. Sci., 2002, 961: 210–215.

[154] Lim, J.H.F. and Davies, G.A., A stochastic model to simulate the growth of anchorage dependent

cells on ﬂat surfaces. Biotechnol. Bioeng., 1990, 36: 547.

[155] Zygourakis, K., Bizios, R., and Markenscoff, P., Proliferation of anchorage dependent contact-

inhibited cells. I. Development of theoretical models based on cellular automata. Biotechnol.

Bioeng., 1991, 38: 459–470.

[156] Zygourakis, K., Markenscoff, P., and Bizios, R., Proliferation of anchorage dependent contact-

inhibited cells. II. Experimental results and comparison to theoretical model predictions.

Biotechnol. Bioeng., 1991, 38: 471–479.

[157] Frame, K.K. and Hu, W.S., A model for density-dependent growth of anchorage-dependent

mammalian cells. Biotechnol. Bioeng., 1988, 32: 1061.

[158] Cherry, R.S. and Papoutsakis, E.T., Modeling of contact-inhibited animal cell growth on ﬂat

surfaces and spheres. Biotechnol. Bioeng., 1989, 33: 300.

[159] Sherratt, J.A., Martin, P., Murray, J.D., and Lewis, J., Mathematical models of wound healing in

embryonic and adult epidermis. IMA J. Math. Appl. Med. Biol., 1992, 9: 177–196.

[160] Sherratt, J.A. and Murray, J.D., Epidermal wound healing: the clinical implications of a simple

mathematical model. Cell Transplant, 1992, 1: 365–371.

[161] Dale, P.D., Maini, P.K., and Sherratt, J.A., Mathematical modeling of corneal epithelial wound

healing. Math. Biosci., 1994, 124: 127–147.

[162] Lee, Y., Mcintire, L.V., and Zygourakis, K., Analysis of endothelial cell locomotion: differential

effects of motility and contact inhibition. Biotechnol. Bioeng., 1994, 43: 622–634.

[163] Dallon, J.C. and Othmer, H.G., A discrete cell model with adaptive signalling for aggregation of

Dictyostelium discoideum. Phil. Trans. R. Soc. Lond. B Biol. Sci., 1997, 352: 391–417.

[164] Hogeweg, P., Evolving mechanisms of morphogenesis: on the interplay between differential

adhesion and cell differentiation. J. Theor. Biol., 2000, 203: 317–333.

[165] Marée, A.F. and Hogeweg, P., How amoeboids self-organize into a fruiting body: multi-

cellular coordination in Dictyostelium discoideum. Proc. Natl Acad. Sci. USA, 2001, 98:

3879–3883.

[166] Palsson, E. and Othmer, H.G., A model for individual and collective cell movement in

Dictyostelium discoideum. Proc. Natl Acad. Sci. USA, 2000, 97: 10448–10453.

[167] Dallon, J.C., Sherratt, J.A., and Maini, P.K., Mathematical modelling of extracellular matrix

dynamics using discrete cells: ﬁber orientation and tissue regeneration. J. Theor. Biol., 1999, 199:

449–471.

[168] Sikavitsas, V.I., Bancroft, G.N., and Mikos, A.G., Formation of three-dimensional cell/polymer

constructs for bone tissue engineering in a spinner ﬂask and a rotating wall vessel bioreactor.

J. Biomed. Mater. Res., 2002, 62: 136–148.

[169] Bancroft, G.N., Sikavitsas, V.I., Van Den Dolder, J., Shefﬁeld, T.L., Ambrose, C.G. et al., Fluid ﬂow

increases mineralized matrix deposition in 3D perfusion culture of marrow stromal osteoblasts in

a dose-dependent manner. PNAS, 2002, 99: 12600–12605.

[170] Belgacem, B.Y., Markenscoff, P., and Zygourakis, K., A computational model for tissue regenera-

tion and wound healing. Proceedings of the 3rd Chemical Engineering Symposium, Athens, Greece,

Vol. 2, pp. 1133–1136, 2001.

[171] Huttenlocher, A.F., Ginsberg, M.H., and Horwitz, A.F., Modulation of cell migration by

integrin-mediated cytoskeletal linkages and ligand-binding afﬁnity. J. Cell Biol., 1996, 134:

1551–1562.

mikos: “9026_c006” — 2007/4/9 — 15:50 — page 21 — #21

Cell Migration 6-21

[172] Palecek, S.P., Loftus, J.C., Ginsberg, M.H., Lauffenburger, D.A., and Horwitz, A.F., Integrin–ligand

binding properties govern cell migration speed through cell–substratum adhesiveness. Nature,

1997, 385: 537–540.

[173] Shin, H., Zygourakis, K., Farach-Carson, M.C., Yaszemski, M.J., and Mikos, A.G., Attachment,

proliferation, and migration of marrow stromal osteoblasts cultured on biomimetic hydrogels

modiﬁed with an osteopontin-derived peptide. Biomaterials, 2004, 25: 895–906.

[174] Gosiewska, A., Rezania, A., Dhanaraj, S., Vyakarnam, M., Zhou, J. et al., Development of a three-

dimensional transmigration assay for testing cell — polymer interactions for tissue engineering

applications. Tissue Eng., 2001, 7: 267–277.

mikos: “9026_c006” — 2007/4/9 — 15:50 — page 22 — #22

mikos: “9026_c007” — 2007/4/9 — 15:50 — page1—#1

Inﬂammatory and

Immune Responses to

Tissue Engineered

Devices

James M. Anderson

Case Western Reserve University

7.1 Introduction.............................................. 7-1

7.2 Inﬂammatory Responses ................................ 7-2

7.3 Immune Responses ...................................... 7-6

References ....................................................... 7-10

7.1 Introduction

Tissue-engineered devices are biologic–biomaterial combinations in which some component of tissue

has been combined with a biomaterial to create a device for the restoration or modiﬁcation of tissue

or organ function. Four signiﬁcant goals must be achieved if these devices are to function adequately

and appropriately in the host environment. These four goals are (1) restoration of the target tissue

with its appropriate function and cellular phenotypic expression; (2) inhibition of the macrophage and

foreign body giant cell foreign body response that may degrade or adversely modify device function;

(3) inhibition of scar and ﬁbrous capsule formation that may be deleterious to the function of the device;

and (4) inhibition of immune responses that may inhibit the proposedfunction of the device and ultimately

lead to the destruction of the tissue component of the tissue-engineered device. The range of types of

tissue-engineered devices is large, yet each device is considered to be unique in its combination of tissue

component and biomaterial, thus requiring a unique set of tests to ensure that the four goals are achieved

for the lifetime of the device in its in vivo environment.

The implantation of a tissue-engineered device activates the host defense systems that include the

inﬂammatory and immune responses. The purpose of this chapter is to provide an overview and fun-

damental understanding of the inﬂammatory and immune responses that may be responsive following

the in vivo implantation of a tissue-engineered device. In general, tissue-engineered devices contain a

biomaterials component for which the evaluation of the inﬂammatory and foreign body reaction is of

importance. Tissue-engineered devices also contain an active biological component, that is, proteins and

cells, for which evaluation of the immune responses is of importance to the overall safety and efﬁcacy of the

tissue-engineered device. In addition, tissue-engineered devices are also considered as combinationdevices

7-1

mikos: “9026_c007” — 2007/4/9 — 15:50 — page2—#2

7-2 Tissue Engineering

TABLE 7.1 The Mononuclear Phagocytic System

Tissues Cells

Implant sites Inﬂammatory macrophages, foreign body giant cells

Liver Kupffer cells

Lung Alveolar macrophages

Connective tissue Histiocytes

Bone marrow Macrophages

Spleen and lymph nodes Fixed and free macrophages

Serous cavities Pleural and peritoneal macrophages

Nervous system Microglial cells

Bone Osteoclasts

Skin Langerhans’ cells, dendritic cells

Lymphoid tissue Dendritic cells

and the interaction between the synthetic and biologic components and their interactive inﬂammatory

and immune responses must be considered and evaluated. For clariﬁcation, it should be noted that the

inﬂammatory responses are also known as the innate immune system and immune responses are generally

considered to be the acquired or adaptive immune system.

The inﬂammatory and immune systems overlap considerably through the activity and phenotypic

expression of macrophages that are derived from blood-borne monocytes. Monocytes and macrophages

belong to the mononuclear phagocytic system (MPS) (Table 7.1). Cells in the MPS may be considered

as resident macrophages in the respective tissues that take on specialized functions that are dependent

on their tissue environment. From this perspective, the host defense system may be seen as blood-borne

or circulating inﬂammatory and immune cells as well as mononuclear phagocytic cells that reside in

speciﬁc tissues with specialized functions. As will be seen in the overview of the inﬂammatory and

immune responses, the macrophage plays a pivotal role in both the induction and effector phases of these

responses.

7.2 Inﬂammatory Responses

The process of implantation of a biomaterial, prosthesis, medical device, or tissue-engineered device results

in injury to tissues or organs and the subsequent perturbation of homeostatic mechanisms that lead to

the cellular cascades of wound healing [1–6]. The response to injury is dependent on multiple factors

including the extent of injury, the loss of basement membrane structures, blood–material interactions,

provisional matrix formation, the extent or degree of cellular necrosis, and the extent of the inﬂammatory

response. These events, in turn, may affect the extent or degree of granulation tissue formation, foreign

body reaction, and ﬁbrosis or ﬁbrous capsule development. These host reactions are considered to be

tissue-, organ-, and species-dependent. In addition, it is important to recognize that these reactions occur

very early, that is, within 2 to 3 weeks of the time of implantation, for biocompatible materials or devices

in the normal resolution of the inﬂammatory and wound healing responses.

Table 7.2 identiﬁes the events in the inﬂammatory responses and indicates the predominant cell type

found in these responses. These characteristic cell types are utilized in histological studies to identify the

phase or event in the inﬂammatory and wound healing sequence of events.

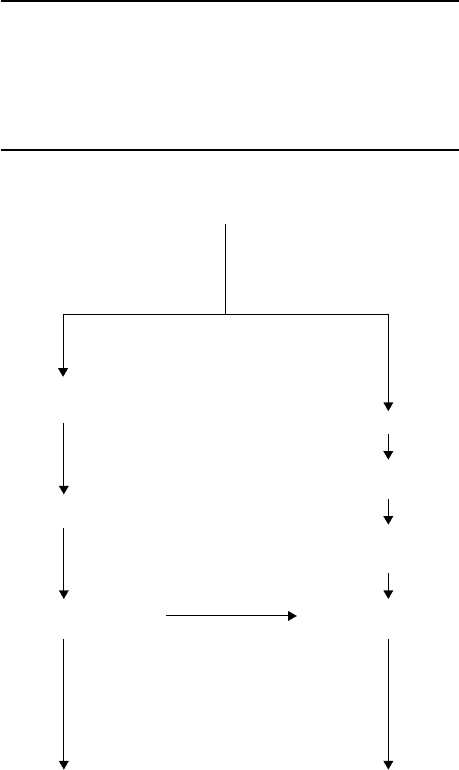
To better appreciate the sequence of inﬂammatory responses that occur within an implant site,

Figure 7.1 illustrates the sequence of events that occur at the tissue/biomaterial interface, that is, for-

eign body reaction, and the events that occur adjacent to the interfacial foreign body reaction and within

the surrounding tissue of the implant site.

Inﬂammation is generally deﬁned as the reaction of vascularized living tissue to local injury, that is,

implantation of a biomaterial, prosthesis, medical device, or tissue-engineered device. Immediately

following injury, blood–material interactions occur and a provisional matrix is formed that consists

mikos: “9026_c007” — 2007/4/9 — 15:50 — page3—#3

Inﬂammatory and Immune Responses 7-3

TABLE 7.2 Principal Cell Types in Inﬂammatory Responses

Response Cell type

Acute inﬂammation Polymorphonuclear leukocyte (neutrophil)

Chronic inﬂammation Monocytes and lymphocytes

Granulation tissue Fibroblasts and endothelial cells (capillaries)

Foreign body reaction Macrophages and foreign body giant cells

Fibrous encapsulation Fibroblasts

Injury, implantation

Inflammatory cell infiltration

Pmns, Monocytes, Lymphocytes

Biomaterial

Exudate/tissue

Acute inflammation

Pmns

Chronic inflammation

Monocytes

Lymphocytes

Fibroblast proliferation

and migration

Granulation tissue

Capillary formation

Th2:IL-4, IL-13

Macrophage fusion

Macrophage mannose

receptor upregulation

Macrophage

differentiation

Monocyte adhesion

Fibrous capsule formation

Foreign body giant

cell formation

FIGURE 7.1 Inﬂammation, wound healing and foreign body responses at the implant site. The biomaterial pathway

occurs at the surface of the biomaterial, whereas the exudate/tissue pathway occurs in the space surrounding the

biomaterial. Both pathways can occur in a simultaneous manner and time frame.

of a platelet/ﬁbrin thrombus/blood clot at the implant surface. As previously indicated, the predomin-

ant cell type (Table 7.2) present in the inﬂammatory response varies with the age of injury. In general,

neutrophils (polymorphonuclear leukocytes) predominate during the ﬁrst several days following injury

and then are replaced by monocytes as the predominant cell type. Three factors occur for this change in cell

type: neutrophils are short-lived and disintegrate and disappear after 24 to 48 h; neutrophil immigration

is of short duration; and chemotactic factors for neutrophil migration are activated early in the inﬂam-

matory response. Following immigration from the vasculature, monocytes differentiate into macrophages

and these cells are very long-lived (up to months). Monocyte immigration may continue for days to weeks

dependent on the injury and implanted device and chemotactic factors for monocytes are activated over

longer periods of time. The size, shape, and chemical and physical properties of the biomaterial or device

mikos: “9026_c007” — 2007/4/9 — 15:50 — page4—#4

7-4 Tissue Engineering

may be responsible for variations in the intensity and duration of the inﬂammatory and wound-healing

processes. Thus, intensity and time duration of the inﬂammatory reaction may characterize the biocom-

patibility of the biomaterial or device. Chemical mediators, released from plasma, cells, and injured tissue

mediate these responses. These mediators include vasoactive amines, plasma proteases, arachidonic acid

metabolites, lysosomal proteases, oxygen-derived free radicals, platelet activating factors, cytokines, and

growth factors.

Acute inﬂammation is dependent on the extent of injury and may be of relatively short duration, lasting

from minutes to days. As seen in Figure 7.1, its main characteristics are the formation of a ﬂuid exudate and

immigration of polymorphonuclear leukocytes across the endothelial lining of blood vessels and into tissue

and the injury (implant) site. Adhesion molecules and receptors present on leukocyte and endothelial

cells facilitate this process that is controlled, in part, by chemotaxis. A wide variety of exogenous and

endogenous substances have been identiﬁed as chemotactic agents. Following localization of leukocytes at

the injury (implant) site, phagocytosis and the release of enzymes occur following activation of neutrophils,

monocytes, and macrophages. The major role of the polymorphonuclear leukocytes in acute inﬂammation

is to phagocytose microorganisms and foreign materials. Phagocytosis is a three-step process in which

the injurious agent undergoes leukocyte attachment, engulfment, and killing or degradation. In regard to

biomaterials, phagocytosis and degradation maynot occur, depending on the properties of the biomaterial.

Biomaterials are not generally phagocytosed by neutrophils or macrophages because of the disparity in size,

that is, the surface of the biomaterial is greater than the size of the cell. In general, particles, microcapsules,

microspheres, or liposomes less than 10 µm in greatest dimension may undergo phagocytosis. The process

of recognition and attachment is expedited when the biomaterial has adsorbed plasma-derived proteins

such as immunoglobulin G (IgG) and the complement-activated fragment, C3b. Fibrinogen has also

been identiﬁed as an adhesion molecule to facilitate leukocyte adhesion to biomaterial surfaces. IgG and

C3b are the two major opsonins. These opsonins are naturally occurring serum factors that facilitate

inﬂammatory cell adhesion. This may be signiﬁcant with tissue-engineered devices in which the synthetic

scaffold material or cell encapsulating synthetic membrane is in direct contact with tissue at the time of

implantation. Thus, depending on the characteristics of the tissue-engineered device, protein adsorption

and cellular adhesion in the inﬂammatory, wound healing and foreign body responses may be important

factors in biocompatibility of the tissue-engineered device as well as its function.

The disparity in size between the biomaterial surface and the adherent cell generally leads to frustrated

phagocytosis, which is the release of cellular enzymes, acid and reactive oxygen and nitrogen intermediates

by either direct extrusion or exocytosis from the cell [7]. These agents may play signiﬁcant roles in the

biodegradation of biodegradable scaffold materials.

Following resolution of the acute inﬂammatory response, chronic inﬂammation with the presence of

monocytes and lymphocytes is predominant. Chronic inﬂammation is characterized by the presence of

monocytes, lymphocytes, and macrophages with the proliferation of blood vessels and connective tissue at

the implant site. With biocompatible materials, the chronic inﬂammatory phase is of short duration and

usually lasts several days and is seen within the ﬁrst week to two weeks following implantation. Persistent

inﬂammatory stimuli and motion of the implant may lead to focal chronic inﬂammation with extended

time periods.

Whereas macrophages and lymphocytes play key roles in immune responses, their presence in the

early inﬂammatory response is generally not considered to be an immune reaction. As will be seen later

under Immune Responses, speciﬁc events in which the macrophages, lymphocytes, and plasma cells

participate can lead to immune responses. Macrophages process and present antigens (foreign materials)

to immunocompetent cells and thus are key mediators in the development of immune reactions.

In the inﬂammatory responses, the macrophage is probably the most important cell in chronic inﬂam-

mation due to the large number of biologically active products that it produces and releases. Important

classes of products produced and secreted by macrophages include neutral proteases, chemotactic factors,

arachidonic acid metabolites, reactive oxygen metabolites, complement components, coagulation factors,

growth-promoting factors, and cytokines. Chemotactic factors, cytokines and growth factors are import-

ant in the development of the next phase of the inﬂammatory and wound healing responses, which is

mikos: “9026_c007” — 2007/4/9 — 15:50 — page5—#5

Inﬂammatory and Immune Responses 7-5

the formation of granulation tissue. Granulation tissue is generally deﬁned as the proliferation of new

small blood vessels and the immigration of ﬁbroblasts into the injury site. Depending on the extent

of injury, granulation tissue may be seen as early as 3 to 5 days following implantation. As seen in

Figure 7.1, at the same time that granulation tissue is being formed, biomaterial adherent macrophages,

derived from monocytes, are fusing to form multinucleated foreign body giant cells on the surface of the

biomaterial [8,9].

The form and topography of the surface of the biomaterial determines the composition of the foreign

body reaction. With biocompatible materials, the composition of the foreign body reaction in the implant

site may be controlled by the surface properties of the biomaterial, the form of the implant, and the

relationship between the surface area of the biomaterial and the volume of the implant. Porous scaffold

materials have high surface-to-volume ratios and can be expected to display large numbers of macrophages

and foreign body giant cells. The foreign body reaction consisting mainly of macrophages and foreign

body giant cells may persist at the tissue/implant interface for the lifetime of the implant.

Macrophages and foreign body giant cells are capable of releasing acid, enzymes, and reactive oxygen

and nitrogen intermediates that can degrade and modify the surfaces to which they are adherent. The

foreign body response with macrophages and foreign body giant cells has been identiﬁed as the principal

cell types responsible for polyurethane biodegradation in clinical devices such as pacemaker leads. It can be

anticipated that macrophages and foreign body giant cells at the surfaces of tissue-engineered devices can

lead to destruction of the device and its components. For these reasons, mitigation and more preferably,

total inhibition, of the foreign body response with macrophages and foreign body giant cells is desirable

for tissue-engineered devices. Although the foreign body response may be inhibited through the use of

pharmacologic agents, that is, dexamethasone, these agents are broad in their action and may adversely

inﬂuence other types of cells and events in the normal wound healing response. Genetic engineering

approaches to modulate macrophage and foreign body giant cell behavior are scientiﬁcally interesting

but may provide tortuous and time-consuming regulatory constraints in their development for human

application. Approaches targeting macrophage adhesion and activation may be helpful in developing

viable tissue-engineered devices. Material surface chemistry may control monocyte adhesion that, of

course, would signiﬁcantly affect subsequent macrophage formation. Also, material surface chemistry may

control adherent macrophage apoptosis, that is, programmed cell death, that renders potentially harmful

macrophages nonfunctional, while the surrounding environment of the implant remains unaffected [10].

The level of adherent macrophage apoptosis appears to be inversely related to the surface’s ability to

promote fusion of macrophages into foreign body giant cells. This appears to be a mechanism by which

adherent macrophages escape apoptosis.

The end-stage healing response to devices is generally ﬁbrosis or ﬁbrous encapsulation. This, of course,

is the replacement of normal or injured tissue by scar or ﬁbrous tissue formation. The replacement of

normal or injured tissue by connective tissue that constitutes the ﬁbrous capsule may be deleterious to

the function of the tissue-engineered device [11,12]. Well-formed ﬁbrous capsules are both acellular and

avascular. The lack of vascularity within the ﬁbrous capsule would certainly indicate that the ﬁbrous

encapsulated tissue-engineered device would not be vascularized and cells in the tissue-engineered device

would eventually undergo ischemic cell death.

It is clear that the end-stage healing response with ﬁbrous encapsulation of the tissue-engineered device

and the presence of the foreign body reaction with macrophages and foreign body giant cells at the

interface between the ﬁbrous capsule and the tissue-engineered device would ultimately lead to failure of

the tissue-engineered device. To achieve viable and functional tissue-engineered devices, at least until the

target tissue or organ has been restored, control of the adverse aspects of the inﬂammatory and wound

healing responses must be achieved. This continues as a challenge for the development of tissue-engineered

devices for human application.

The inﬂammatory (innate) and immune (adaptive) responses have common components. It is possible

to have inﬂammatory responses only with no adaptive immune response. In this situation, both humoral

and cellular components that are shared by both types of responses may only participate in the inﬂam-

matory response. Table 7.3 indicates the common components to the inﬂammatory (innate) and immune

mikos: “9026_c007” — 2007/4/9 — 15:50 — page6—#6

7-6 Tissue Engineering

TABLE 7.3 Common Components in the Inﬂammatory

(Innate) and Immune (Adaptive) Responses

Humoral components

Complement cascade components

Immunoglobulins

Cellular components

Macrophages

NK (natural killer) cells

Dendritic cells

Cells with dual phagocytic and antigen presenting capabilities

TABLE 7.4 Cell Types and Function in the Adaptive Immune System

Cell type Function

Macrophages (APC) Process and present antigen to immunocompetent T cells

phagocytosis

Activated by cytokines, that is, IFN-γ , from other immune cells

T cells Interact with antigen presenting cells (APCs) and are activated through

two required cell membrane interactions

Facilitate target cell apoptosis

Participate in transplant rejection (Type IV hypersensitivity)

B cells Form plasma cells that secrete immunoglobulins (IgG, IgA, and IgE)

Participate in antigen–antibody complex mediated tissue

damage (Type III hypersensitivity)

Dendritic cells (APC) Process and present antigen to immunocompetent T cells

Utilize Fc receptors for IgG to trap antigen–antibody complexes

NK (natural killer) cells Innate ability to lyse tumor, virus infected, and other

(Non-T, Non-B lymphocytes) cells without previous sensitization

Mediates T and B cell function by secretion of IFN-γ

(adaptive) responses. Macrophages are known as professional antigen presenting cells responsible for the

initiation of the adaptive immune response.

7.3 Immune Responses

The acquired or adaptive immune system acts to protect the host from foreign agents or materials and

is usually initiated through speciﬁc recognition mechanisms and the ability of humoral and cellular

components to recognize the foreign agent or material as being “nonself ” [11–15]. Generally, the adaptive

immune system may be considered as having two components: humoral or cellular. Humoral components

include antibodies, complement components, cytokines, chemokines, growth factors, and other soluble

mediators. These humoral components are synthesized by cells of the immune response and, in turn,

function to regulate the activity of these same cells and provide for communication between different

cells in the cellular component of the adaptive immune response. Cells of the immune system arise from

stem cells in the bone marrow (B lymphocytes) or the thymus (T lymphocytes) and differ from each

other in morphology, function and the expression of cell surface antigens (Table 7.4). They share the

common features of maintaining cell surface receptors that assist in the recognition and elimination of

foreign materials. Regarding tissue-engineered devices, the adaptive immune response may recognize

the biological components, modiﬁcations of the biological components, or degradation products of the

biological components, commonly known as antigens, and initiate immune response through humoral

or cellular mechanisms.

mikos: “9026_c007” — 2007/4/9 — 15:50 — page7—#7

Inﬂammatory and Immune Responses 7-7

TABLE 7.5 Effector T Lymphocytes in Adaptive Immunity

TH1 helper cells CD4+

Proinﬂammatory

Activation of macrophages

Produces IL-2, interferon-γ (IFN-γ ), IL-3, tumor necrosis factor-α, GM-CSF, macrophage

chemotactic factor (MCF), migration inhibitor factor (MIF) induce IgG2a

TH2 helper cells CD4+

Anti-inﬂammatory

Activation of B cells to make antibodies

Produces IL-4, IL-5, IL-6, IL-10, IL-3, GM-CSF, and IL-13

Induce IgG1

Cytotoxic T cells (CTL) CD8+

Induce apoptosis of target cells

Produce IFN-γ , TNF-β, and TNF-α

Release cytotoxic proteins

Components of the humoral immune system play important roles in the inﬂammatory responses to

foreign materials. Antibodies and complement components C3b and C3bi adhere to foreign materials,

act as opsonins and facilitate phagocytosis of the foreign materials by neutrophils and macrophages that

have cell surface receptors for C3b. Complement component C5a is a chemotactic agent for neutrophils,

monocytes, and other inﬂammatory cells and facilitates the immigration of these cells to the implant site.

The complement system is composed of classic and alternative pathways that eventuate in a common

pathway to produce the membrane attack complex (MAC), which is capable of lysing microbial agents.

The complement system, that is, complement cascade, is closely controlled by protein inhibitors in the

host cell membrane that may prevent damage to host cells. This inhibitory mechanism may not function

when nonhost cells are used in tissue-engineered devices.

The T (thymus-derived) lymphocytes are signiﬁcant cells in the cell-mediated adaptive immune

response and their cell-adhesion molecules play a signiﬁcant role in lymphocyte migration, activation

and effector function. The speciﬁc interaction of cell membrane adhesion molecules, sometimes also

called ligands or antigens, with antigen-presenting cells produce speciﬁc types of lymphocytes with spe-

ciﬁc functions. Table 7.4 indicates cell types and function in the adaptive immune response. Obviously,

the functions of these cells are more numerous than indicated in Table 7.4 but the major function of these

cells is provided to indicate similarities and differences in the interaction and responsiveness of these cells.

Effector T cells (Table 7.5) are produced when their antigen-speciﬁc receptors and either the CD4 or the

CD8 co-receptors bind to peptide-MHC (major histocompatibility complex) complexes. A second, co-

stimulatory signal is also required and this is provided by the interaction of the CD28 receptor on the T cell

and the B7.1 and B7.2 glycoproteins of the immunoglobulin superfamily present on antigen-presenting

cells. B lymphocytes bind soluble antigens through their cell-surface immunoglobulin and thus can func-

tion as professional antigen-presenting cells by internalizing the soluble antigens and presenting peptide

fragments of these antigens as MHC:peptide complexes. Once activated, T cells can synthesize the T cell

growth factor interleukin-2 and its receptor. Thus, activated T cells secrete and respond to interleukin-2

to promote T cell growth in an autocrine fashion.

Cytokines are the messenger molecules of the immune system. Most cytokines have a wide spectrum

of effects, reacting with many different cell types, and some are produced by several different cell types.

Table 7.6 presents common categories of cytokines and lists some of their general properties. It should

be noted that while cytokines can be subdivided into functional groups, many cytokines such as IL-1,

TNF-α, and IFN-γ are pleotropic in their effects and regulate, mediate, and activate numerous responses

by numerous cells.

Cytokines produce their effects in three ways. The ﬁrst type of effect is the autocrine effect in which

the cytokine acts on the same cell that produced it. An example is when IL-2 produced by activated

T cells promotes T-cell growth. The second way is when a cytokine affects other cells in its vicinity. This