Финаев В.И. Аналитические и имитационные модели
Подождите немного. Документ загружается.

61
непреодолимое препятствие – нестабильность электронных
элементов, на которых осуществлялась реализация
датчиков случайных чисел. Из-за нестабильности эти
датчики необходимо было постоянно настраивать.
Появление высокопроизводительной вычислительной
техники и развитых языков программирования упростило
задачу создания эталонов. Датчики или генераторы
случайных чисел стали создавать программным путем. В
библиотеках языков программирования присутствуют
подпрограммы (процедуры) с названиями random,
randomizir, randu и прочее, которые позволяют получать на
ЭВМ псевдослучайные числа, квазиравновероятно
распределенные в интервале [0, 1].
Строго говоря, для формирования случайных событий с
различными функциями распределения в ЭВМ необходимо
иметь, как эталон, совокупность случайных чисел с
равномерным законом распределения. Эта совокупность
случайных чисел будет эталоном, т.е. базовой
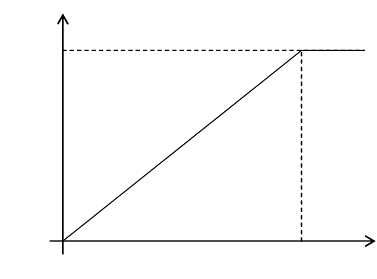
последовательностью случайных чисел. На рис. 4.1 показан
вид функции распределения случайных чисел, равномерно
(равновероятно) распределенных в интервале [0, 1].
F(x)
х
1
1 0
Рис. 4.1

62
Функция распределения вероятностей случайных чисел,
равномерно распределенных в интервале [0, 1], имеет вид
⎪
⎩
⎪
⎨
⎧
>
<≤
<
=
1.x ,1
1;x0 ,x
0;x ,0
)x(F
(4.1)
Математическое ожидание (генеральное среднее)
случайных чисел, равномерно распределенных в интервале
[0, 1], будет равно M[х]=0,5, а дисперсия D[х]=1/12.
Однако применение возможностей ЭВМ не позволяет
теоретически получить последовательность случайных
чисел с равномерным распределением. Действительно,
любое число в ЭВМ формируется в регистре. Если число
разрядов регистра ЭВМ равно k, то число Х в десятеричной
системе счисления будет сформировано согласно формуле
,
∑
−
=
=
1k
0j
j
j
2αX
(4.2)
в которой коэффициенты α
i
∈{0, 1} составляют двоичный
код α
k-1
,α
k
,…,α
2
,α
1
,α
0
случайного десятеричного числа Х.
Десятеричное число Х будет случайным и будет иметь
равномерное распределение, если коэффициенты α
i
=0 с
вероятностью р
i
=0,5 или α
i
=1 с вероятностью р
i
=1-0,5.
Тогда числа Х={i/(2
k
-1)} принимают значения i/(2
k
-1)
(i=0,1,2,...,2
k
-1) с постоянной вероятностью Р=1/2
k
.
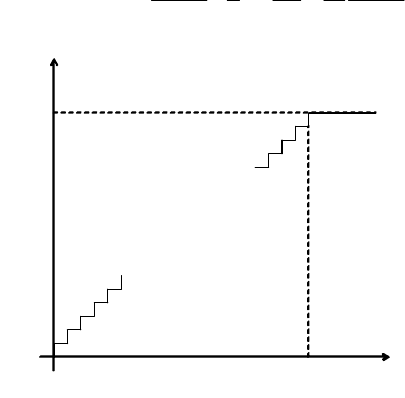
Но полученные при этих условиях случайные числа Х
будут иметь не равномерное, а квазиравномерное
равновероятностное распределение в интервале [0,1], вид
которого показан на рис. 4.2, что связано с дискретностью
чисел Х. Математическое ожидание и дисперсия для
данного распределения определяются соотношениями:
∑
−
=
=⋅
−
=
1
k
2
0i
0,5,
k
2
1
1
k
2
i
M[x]
(4.3)
63
1
k
2
1
k
2
12
1
k
2
1
1
k
2
0i
2
)
2
1
1
k
2
i
(D[x]
−
+
=⋅
−
=
−
−
=
∑
. (4.4)
F(x)
х
1
1 0
Рис. 4.2
Таким образом, математическое ожидание
квазиравномерного равновероятностного распределения в
интервале [0,1] M[х] точно совпадает с генеральным
средним для равномерного распределения в интервале
[0,1], а дисперсия при kÆ∞ асимптотически стремится к
дисперсии для равномерного распределения, равной 1/12.
Практически при k>15 обеспечивается требуемая точность
в имитационных исследованиях.
В ЭВМ нет генератора случайных чисел α
i
,
принимающих значения либо 0, либо 1 с вероятностью
Р=1/2, поэтому аппаратная реализация датчика не имеет
смысла. Датчики случайных чисел разрабатывают в виде
программ, поэтому случайные числа, получаемые на ЭВМ,
не являются случайными. Эти числа формируются на
основе детерминированных преобразований в виде
алгоритмов, поэтому их называют псевдослучайными. Так
64
как алгоритм представляет собой строгую
последовательность действий, то последовательность,
получаемых псевдослучайных, квазиравномерно
распределенных в интервале [0,1] чисел, имеет период Р,
например: Х
0
, Х
1
, Х
2
, Х
3
,...,Х
Р-2
, Х
Р-1
, Х
Р
, Х
0
, Х
1
, Х
2
, Х
3
,...
Датчики псевдослучайных, квазиравномерно
распределенных в интервале [0,1] чисел создают таким
образом, чтобы период Р был как можно более большим и
превосходил в несколько раз число испытаний (опытов),
производимых на ЭВМ в имитационной программе. Если
при моделировании число обращений к программному
датчику случайных чисел оказывается меньше периода,
измеряемого числом различных случайных чисел, то такая
периодичность программного датчика не оказывает
существенного влияния на результаты моделирования.
Рассмотрим, каким образом можно создавать алгоритмы
для получения псевдослучайных, квазиравномерно
распределенных чисел. Методы получения
псевдослучайных квазиравномерных чисел программным
путем делятся на две группы:
а) аналитические;
б) методы перемешивания.
При использовании аналитических методов в
псевдослучайной последовательности Х
0
, Х
1
, Х
2
, …, Х
r-1
очередное число Х
r
получают с помощью некоторого
выбранного рекуррентного соотношения ϕ, аргументами
которого являются одно или несколько предыдущих чисел
последовательности, т.е. Х
r
=ϕ(Х
r-1
, Х
r-2
,..., Х
0
).
Самым простым примером может служить метод
вычетов, в котором для получения числа Х
i+1
используется
следующее рекуррентное соотношение:
Х
i+1
=bХ
i
(mod M), (4.5)
где выражение bХ
i
(mod M) означает остаток от деления
произведения
bХ
i
на число M; Х
i+1
- очередное случайное
65
число; Х
i
- предыдущее случайное число; b - некоторая
константа; M - число, определяющее значение получаемых
случайных чисел.
Рассмотрим пример. Пусть очередное число Х
i+1
определяется по формуле
⎢
⎣
⎡
⎥
⎦
⎤
+
⎟
⎠
⎞
⎜
⎝
⎛
=
−
+
2
i
Bx
i
x
e
xcos
A
i
1i
X , (4.6)
где А и В заданные константы, ]Х
i+1
[ - операция взятия
мантиссы числа Х
i+1
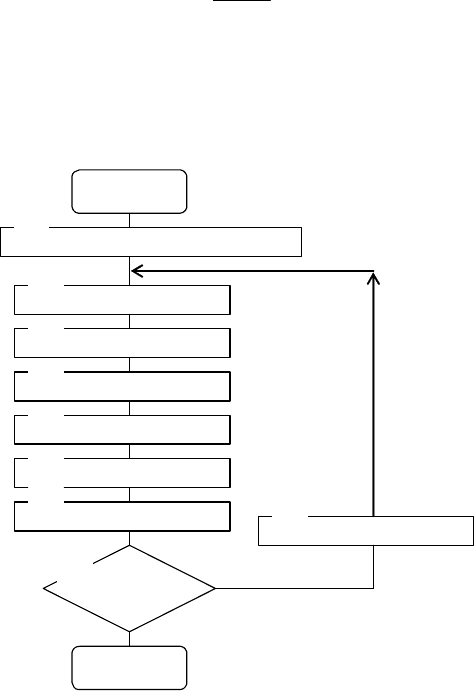
. На рис. 4.3 приведен алгоритм
генератора псевдослучайных, квазиравномерно
распределенных чисел в интервале [0,1].
Вывод X[T+1]
X[T+1]=]A
×
F+G[
6
7
G=X[T]
2
5
F=D/E
4
E=e
B
×
X[T]
3
1
0
Ввод T=0, TZ, Х[T], А, В
1
T
≤
TZ
8
Т=Т+1
9
Начало
D=cosX[Т]
2
Конец
Рис. 4.3
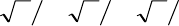
66
В блоке 1 алгоритма осуществляется задание начального
такта моделирования Т=0, заданное число тактов
моделирования (генерации) TZ, равное количеству чисел
Х, которое должно быть получено от датчика. В блоках 2-6
вычисляется очередное число Х[T+1]. В блоке 8
проверяется условие генерации датчиком заданного числа
чисел Х. Если условие Т≤TZ выполняется, то
наращивается в блоке 9 такт моделирования. Таким
образом, генератор псевдослучайных, квазиравномерно
распределенных чисел может быть реализован согласно
заданной формуле (4.6).
При применении методов перемешивания очередное
число псевдослучайной последовательности получается
путем хаотического перемешивания разрядов предыдущего
случайного числа с помощью операций сдвига,
специального сложения и других различных
арифметических операций. В качестве начальной
константы Х
0
для формирования последовательностей
обычно берут иррациональные числа (
55,22,33
).
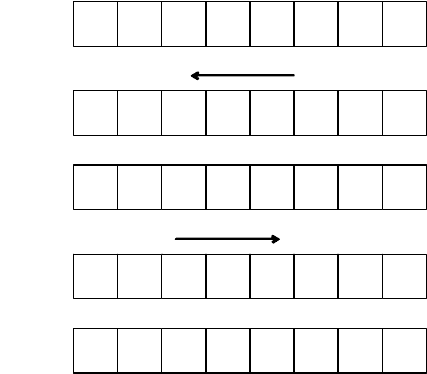
На рис. 4.4 показан пример метода перемешивания.
Число Х
i
вначале циклически сдвигается на три разряда
влево (K=3), а затем полученное после этого сдвига число
поразрядно суммируется по модулю два с начальным
числом Х
i
. Получаем двоичное число Х
i
*.
Затем это число циклически сдвигается на два разряда
вправо (L=2) и полученный результат суммируется
поразрядно по модулю два с числом Х
i
*. В результате
получим последующее число псевдослучайной
последовательности Х
i+1
.
Приведенная процедура легко алгоритмизируется, а
затем по алгоритму составляется программа,
представляющая собой датчик псевдослучайных,
квазиравномерно распределенных чисел.
67
Сдвиг на два разряда вправо
Сдвиг на три разряда влево
Х
i
0 11 10 01 1
1 01 11 00 1
1 10 01 01 0
⊕
=
0 01 01 01 1
⊕
=
1 11 00 00 1
Х
i+1
Х
i
*
Рис. 4.4
Для того чтобы числа были распределены в интервале
[0,1], необходимо провести соответствующее
нормирование, например, считать, что получаемые числа
это дробная часть.
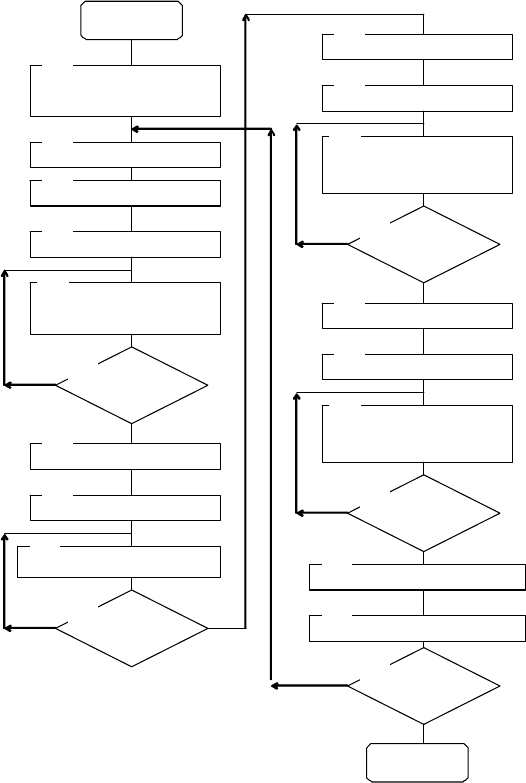
На рис. 4.5 приведен алгоритм датчика
псевдослучайных, квазиравномерно распределенных чисел,
реализованного согласно примеру метода перемешивания.
В блоке 1 алгоритма осуществляется ввод начального
такта моделирования Т=0, заданное число тактов
моделирования (генерации) TZ, начального массива Х0[I]
размерностью IM, значение IM, а также K - число сдвигов
влево и L - число сдвигов вправо. В массиве Х0[I] записана
начальная константа Х
0
. В блоках 3-6 определяется массив
ХK[I], полученный из массива Х0[I] в результате
циклического сдвига его элементов на K разрядов влево.
Например, если
IM=7, а K=3, то при I=0 (блок 4)
ХK[3]=Х0[0] (блок 5), при I=1 ХK[4]=Х0[1], при I=2
ХK[5]=Х0[2], при I=3 ХK[6]=Х0[3], при I=4 ХK[0]=Х0[4],
68
при I=5 ХK[1]=Х0[5], при I=6 ХK[2]=Х0[6]. Результатом
операции (I+K)modIM будет остаток от деления числа I+K
на число IM.
Ввод T=0, TZ,
Х0[I], IM, K, L
1
I=I+1
4
Начало
I=-1
3
Конец
T=T+1
2
XK[(I+K)modIM]=
=X0[I]
5
1
0
I<IM-1
6
I=I+1
8
I=-1
7
XM[I]=X0[I]
⊕
XK[I]
9
1
0
I<IM-1
10
I=I+1
12
I=-1
11
XL[I]=
+XM[(I+L)modIM]
13
1
0
I<IM-1
14
I=I+1
16
I=-1
15
XT[I]=XM[I]
⊕
⊕XL[I]
17
1
0
I<IM-1
18
Вывод массива XT[I]
19
1
0
T<TZ
21
X0[I]=XT[I]
20
Рис. 4.5
69
Затем в блоках 7-10 алгоритма происходит поразрядное
суммирование по модулю два элементов массивов ХK[I] и
Х0[I]. В результате будет получен массив ХМ[I].
В блоках 11-14 определяется массив ХL[I], полученный
из массива ХM[I] в результате циклического сдвига его
элементов на L разрядов вправо. Например, при L=2, при
I=0 (блок 12) ХL[0]=ХM[2] (блок 13), при I=1
ХL[1]=ХM[3], при I=2 ХL[2]=ХM[4], при I=3
ХL[3]=ХM[5], при I=4 ХL[4]=ХM[6], при I=5
ХL[5]=ХM[0], при I=6 ХL[6]=ХM[1].
Затем в блоках 15-18 алгоритма происходит поразрядное
суммирование по модулю два элементов массивов ХМ[I] и
ХL[I]. В результате будет получен массив ХT[I], элементы
которого представляют собой двоичный код мантиссы
искомого псевдослучайного, квазиравномерно распреде-
ленного в интервале [0,1] числа. В блоке 19 элементы
массива ХT[I] присваиваются элементам массива Х0[I]. В
блоке 21 выполняется условие генерации датчиком
заданного числа чисел Х.
Насколько близким к теоретическому равномерному
распределению является программный датчик
псевдослучайных, квазиравномерно распределенных чисел
проверяют на основе анализа результатов статистической
проверки.
4.3. Проверочные тесты
Программная реализация датчика псевдослучайных,
квазиравномерно распределенных чисел может быть
получена любым программистом на основе разработанного
им алгоритма с применением либо аналитических методов,
либо методов перемешивания. Качество датчика
необходимо проверить. Осуществляются проверки путем

70
применения проверочных тестов. Рассмотрим проверочные
тесты.
Тест частот. Отрезок [0,1] разбивается на m (обычно 10-
20) равных интервалов, как это показано на рис. 4.6.
0
n
1
1
….
1 2 3 m
n
2
n
3
n
m
Рис. 4.6
Датчик псевдослучайных, квазиравномерно
распределенных чисел генерирует N величин, каждая из
которых принадлежит одному из m отрезков.
В результате проведения N испытаний будут получены
эмпирические частоты n
i
, представляющие собой число
попаданий чисел датчика в интервал i, i=
m,1
. Деление
частот n
i
на число опытов N даст эмпирические частоты.
Если рассматривать теоретическое равномерное
распределение случайной величины на отрезке [0,1], то
теоретические вероятности попадания в каждый из m
отрезков одинаковы и равны значению 1/m.
Для проверки согласия датчика псевдослучайных,
квазиравномерно распределенных чисел и теоретического
равномерного распределения полученные эмпирические
частости n
i
/N, (i=
m,1
),
N)
m
1i
i
n( =
=
∑
сравнивают с
теоретическими вероятностями 1/m. Согласие проверяется
по критерию χ
2
, т.к. случайная величина
∑
=
−
=
k
1i
i
Np
2
)
i
Np
i
(n
2
χ
(4.7)
подчиняется распределению χ
2
с (m-1) степенями свободы,
где N - объем выборки (число опытов).
