Финаев В.И. Аналитические и имитационные модели
Подождите немного. Документ загружается.


31
точку
)z,...,z,z(Z
0
n
0
2
0
10
=
, символом F. Тогда модель в виде
функции переходов для динамической системы будет
задана в общем виде уравнением
) )]t(X(,Z,t,t(F)t(Z
t
o
t00
=
. (2.9)
Эта функция каждому набору
) )]t(X(,Z,t,t(
t
o
t00
ставит в
соответствие то состояние Z(t), в которое переходит
система за время перехода t-t
0
из фазы (t
0
,Z
0
) под
действием входных параметров
t
o
t
)]t(X(
.
Модель динамической системы в виде функции выходов
в общем виде будет определена уравнением
),)]t(X(,Z,t,t(G)t(y
t
o
t00
=
(2.10)
в котором оператор G каждому набору
))]t(X(,Z,t,t(
t
o
t00
сопоставляет выходной сигнал y
t
=y(t).
Дифференциальные уравнения классифицируются на
линейные и нелинейные, стационарные и нестационарные,
уравнения первого и более высокого порядка, а также
одномерные и многомерные.
Если модель предназначена для описания изменения
состояния z(t) динамической системы, то модель в виде
обыкновенного линейного дифференциального уравнения
q-го порядка с постоянными коэффициентами и правой
частью, выраженной через производные от управляющих
функций, задается в следующем виде:
=λ−−λ−λ−
−
−
−
−
z...
dt
zd
dt
zd
dt
zd
q
2q
2q
2
1q
1q
1
q
q
x...
dt
xd
dt
xd
dt
xd
r
2r
2r
2
1r
1r
1
r
r
0
μ++μ+μ+μ=
−
−
−
−
(2.11)
Если применить оператор дифференцирования
dt
d
p =
,
то с учетом аддитивной ошибки v(t) уравнение (2.11)
запишется в виде

32
z(р)=λ
-1
(р)μ(р)х(р)+v(р),
где λ
-1
(р)=р
q
-λ
1
р
q-1
-λ
2
р
q-2
-…-λ
q
, μ(р)=μ
0
р
r
+μ
1
р
r-1
+ … + μ
r
.
Модели в виде многомерных дифференциальных
уравнений в форме Коши находят наибольшее применение.
Они описываются системами обыкновенных
дифференциальных уравнений первого порядка в форме
Коши, т.е. разрешенными относительно первых
производных. Для стационарной линейной системы,
параметры которой изменяются непрерывно во времени,
модель в общей форме имеет следующий вид:
dZ
= ФZ+GX+ГW, Y = HZ + V
dt
. (2.12)
В уравнении (2.12): Z={z
1
(t),z
2
(t),…,z
n
(t)} - вектор
состояний; Х(t)={х
1
(t),х
2
(t),...,х
m
(t)} – вектор входных
параметров; Y(t)={y
1
(t),y
2
(t),..., y
r
(t)} – вектор выходных
параметров; W={w
1
(t),w
2
(t),…,w
n
(t)} - вектор шума
системы;
T
12 n
dZ dz dz dz
= { , ,..., }
dt dt dt dt
- транспонированный
вектор производных от переменных состояния; матрицы Ф,
G, H
и Г имеют размерности, зависящие от размерностей
векторов Z, Х(t), Y(t), W. Коэффициенты матриц Ф, G, H и
Г имеют смысл коэффициентов передачи, для
стационарной системы не зависят от времени и подлежат
оцениванию. Параметры могут входить и в начальное
условие, которое необходимо добавить для решения
первого уравнения (2.12).
Модель для нестационарной линейной непрерывной
системы отличается от (2.12) тем, что матрицы Ф, G, H и Г
будут зависеть от времени.
Непрерывная нелинейная система может быть описана
моделью
V.),t,X,Z(Y ,W),t(Г),t,X,Z(
dt
dZ
+Θψ=Θ+Θϕ=
(2.13)
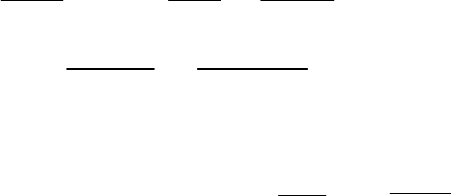
33
Векторные функций ϕ(…), ψ(…) и матрица Г(...)
предполагаются известными с точностью до параметров,
подлежащих оцениванию. Применяя преобразования
Лапласа, можно перенести описание из временной области
в область изображений по Лапласу.
Компьютерное моделирование систем, описываемых
многомерными дифференциальными уравнениями в форме
Коши, осуществляется с применением пакетов программ.
Широко используется подсистема Simulink пакета MatLab.
При моделировании определяется вид дифференциального
уравнения, задаются начальные условия. Результаты
решения отображаются визуально в виде цифровых
данных, а также в виде графических данных.
2.3. Инерционные модели
Динамические системы с последействием (с
предысторией) могут быть формализованы с применением
дифференциальных уравнений с запаздывающим
аргументом.
2.3.1. Дифференциальные уравнения с
запаздывающими аргументами.
В общем случае
дифференциальные уравнения n-го порядка с
запаздывающим аргументом имеют вид
nn-1
nn-1
d z(t) dz(t) d z(t)
= f[t, z(t), ,..., ,z(t - τ),
dt dt dt
n-1
n-1
dz(t - τ)dz(t-τ)
,..., ]
dt dt
. (2.14)
Дифференциальное уравнение (2.14) может быть
сведено к системе дифференциальных уравнений первого
порядка. Введем обозначения:
z=z
1
;
2
dz(t)
=z
dt
;
2
3
2
dz (t)
=z
dt
и

34
т.д. Тогда дифференциальное уравнение (2.14) запишем в
следующем виде:
n
12 n1 2 n
dz(t)
= f[t, z (t), z (t),...,z (t),z (t - τ), z (t - τ),..., z (t - τ)]
dt
.
Из рассмотрения даже простейшего дифференциального
уравнения вида
)]t(z),t(z,t[f
dt
)t(dz
τ−=
, (2.15)
где τ>0, τ=сonst, сложно понять, какие начальные условия
надо задать, чтобы определить решение z(t) для t>t
0
.
Решение дифференциального уравнения (2.15)
определяется из интегрального уравнения
∫
Θτ−ΘΘΘ+=
t
0
t
0
.d)](z),(z,[f)t(z)t(z
(2.16)
Решение уравнения (2.16) осуществляется по
следующему алгоритму.
Следует задать начальное значение для точки t
0
z
0
=z(t
0
)
и функцию z(t) в полуинтервале t
0
-τ≤t<t
0
([t
0
-τ, t
0
)).
Функцию z(t)=W(t) называют начальной функцией ∀t∈[t
0
-
τ,t
0
). При таких условиях можно получить либо
аналитическое решение уравнения (2.16), либо получить
решение для любого Θ>t
0
с применением методов
вычислительной математике и компьютерного
моделирования. Алгоритм решения уравнения (2.16)
представляет собой следующую последовательность
действий.
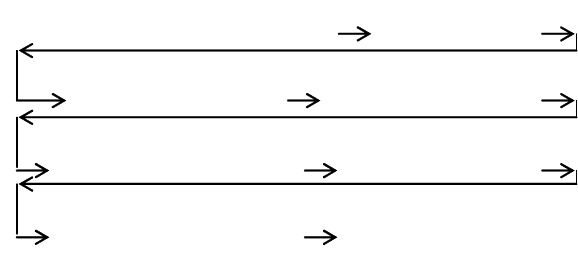
После задания начальных условий следует определить
непрерывное решение z(t) для t>t
0
, при условии, что
z(t)=W(t) для ∀t∈[t
0
-τ,t
0
). Если функции f и W непрерывны
и первая из них удовлетворяет условию Липшица по z, то
искомое решение существует и единственно.
35
Зная W(t) для t
0
-τ≤t<t
0
, найдем z(t) для t
0
≤t<t
0
+τ.
Примем это z(t) за начальную функцию W(t) для t
0
≤t<t
0
+τ.
Определим z(t) для t
0
+τ≤t<t
0
+2τ и т.д.
При поиске решения применен метод последовательного
интегрирования, сущность которого показана на рис. 2.3.
Дифференциальные уравнения с запаздывающим
аргументом применяются для составления моделей
динамической системы с последствием, т.е. систем, для
определения состояний z(t) которых при t>t
0
недостаточно
задать z
0
=z(t
0
).
∀
t
∈
[t
0
+2
τ
,t
0
+3
τ
): z(t)
z
0
=z(t
0
),
∀
t
∈
[t
0
-
τ
,t
0
): z(t)=W(t)
∀
t
∈
[t
0
,t
0
+
τ
): z(t)
z(t)=W(t)
∀
t
∈
[t
0
,t
0
+
τ
)
∀
t
∈
[t
0
+
τ
,t
0
+2
τ
): z(t)
z(t)=W(t)
∀
t
∈
[t
0
+
τ
,t
0
+2
τ
)
z(t)=W(t)
∀
t
∈
[t
0
+2
τ
,t
0
+3
τ
)
………
Рис. 2.3
2.3.2. Модели в виде сумм и интегралов свертки. Если
динамическая система функционирует в дискретные
моменты времени, то ее модель может быть описана в виде
суммы свертки. Математические модели, выражаемые
суммой свертки или интеграла свертки, задаются
следующим образом. Для однооткликовой стационарной
динамической системы, на вход которой действует
управляющая функция х(t), а наблюдения над входом и
выходом производятся только в дискретные моменты
времени с интервалом квантования Δt, математическая
модель может быть выражена с помощью суммы свертки:
36
=Δ+
∑
Δ−ΔΔ=Δ
∞
=
)tk(v)titk(x)ti(h)tk(z
0i
).tk(v)ti(x)titk(h
k
i
Δ+
∑
ΔΔ−Δ=
−∞=
Зададим масштаб t=1, получим
=+
∑
−=
∞
=
)k(v)ik(x)i(h)k(z
0i
).k(v)i(x)ik(h
k
i
+
∑
−=
−∞=
(2.17)
Модель (2.17) является моделью импульсной системы,
h(i) есть импульсная характеристика системы,
представляющая собой отклик системы в данный момент
времени на входное воздействие, приложенное на i
интервалов раньше и имевшее характер единичного
мгновенного импульса в виде функции Дирака.
Импульсная характеристика играет здесь роль весовой
функции.
Если линейная динамическая система нестационарная,
то в выражения (2.17) нельзя применять импульсную
характеристику системы вида h(k-i). Для этого случая
математическая модель примет вид
),k(v)i(x)i,k(h)k(z
k
i
+
∑
=
−∞=
где h(k,i) - реакция системы в момент k на единичный
импульс в момент i.
В модели типа суммы свертки роль величин,
подлежащих определению из экспериментальных данных,
играют значения импульсной характеристики, т.к. данная
модель является непараметрической, т.е. не содержит явно
параметров в виде некоторых численных величин. Если в
динамической системе измерения управляющей функции и
отклика носят непрерывный характер, то модель линейной
системы может
быть записана в виде интеграла свертки:
37
- для линейной системы
∞
∞
∫∫
t
τ=0 τ=-
z(t) = h(τ)x(t - τ)dτ +v(t)= h(t-τ)x(τ)dτ + v(t)
; (2.18)
- для нестационарной системы
∫
+τττ=
−∞=τ
t
).t(vd)(x),t(h)t(z
Модель представлена в виде функционала с аддитивной
ошибкой v(t). Интеграл называется интегралом свертки,
или интегралом Дюамеля. Для определения импульсной
характеристики (весовой функции) используется (для
стационарных систем) представление весовой функции в
форме Релея-Ритца путем разложения функций в ряд по
системе известных ортогональных функций
,)t(Ф),t(h
p
1i
ii
∑
Θ=Θ
=
(2.19)
где Ф
i
(t) - функции системы ортогональных функций при
значениях t, принадлежащих отрезку ортогональности
[t
1
,t
2
]. Это позволяет сделать модель параметрической,
которая содержит ограниченное число параметров Θ
i
,
подлежащих определению. Коэффициенты Θ
i
называют
еще спектром разложения в ряд базисных функций.
К системе базисных функций предъявляются следующие
требования: для любой весовой функции ряд (2.19) должен
сходиться; Ф
i
(t) должна иметь простую аналитическую
форму; Θ
i
должны вычисляться аналитически просто.
Условие ортогональности базисных функций имеет вид
≠
⎧
⎫
⎨
⎬
⎩⎭
∫
2
1
t
ij
i
t
0i
j
Ф (t)Ф (t)dt =
ci=
j
, (2.20)
где число с
i
называют нормой базисной функции Ф
i
(t).
Каждую базисную функцию можно нормировать по ее
норме, причем нормированная функция имеет вид
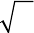
38
iii
Ф (t) = Ф (t)/ c
.
Система (2.20) примет вид
⎧⎫
⎨⎬
≠
⎩⎭
∫
2
1
t
ij ij
i
t
1i=j
Ф (t)Ф (t)dt = = δ
0ij
, (2.21)
где δ
ij
- символ Кронекера.
Для определения Θ
i
умножим правую и левую части
уравнения (2.19) на Ф
i
(t) и проинтегрируем обе части на
отрезке ортогональности
∞
∑
∫∫
22
11
tt
ikki
k=0
tt
h(t)Ф (t)dt = ΘФ(t)Ф (t)dt
.
При k=i правый интеграл равен единице, тогда
∫
2
1
t
ii
t
Θ =S(t)Ф (t)dt
. (2.22)
Модели вида свертки могут использоваться и для
описания многооткликовых линейных инерционных
систем.
2.4. Модели на основе передаточных функций
Рассмотрим однооткликовую импульсную систему с
дискретными сигналами на ее входе и выходе, модель
которой может быть выражена с помощью импульсной
характеристики (весовой функции) в виде уравнения (2.17).
Дискретное Z-преобразование решетчатой функции
v(n)=v
n
задается в следующем виде
ˆ
∞
∑
-n
n
n=0
v(z) = v z
.
Применяя одностороннее Z-преобразование к левой и
правой части этого выражения, получаем
39
ˆ
ˆˆˆ
z(z) = h(z)x(z) + v(z)
/ (2.23)
Z-преобразование однозначно связано с дискретным
преобразованием Лапласа. Взаимосвязь комплексной
переменной z и комплексной переменной преобразования
Лапласа выражается соотношением z=e
s
, которое
используется для перехода от дискретного преобразования
Лапласа к Z-преобразованию и наоборот.
Модель импульсной системы (2.23) устанавливает связь
между Z-преобразованием
)z(z
ˆ
отклика z(k) выходного
сигнала и Z-преобразованием
)z(x
ˆ
входного сигнала х(k).
)z(h
ˆ
- передаточная функция импульсной системы
(дискретная передаточная функция), являющаяся Z-
преобразованием импульсной характеристики h(k).
)z(v
ˆ
-
Z-преобразование случайной составляющей v(k).
Если применять преобразование Лапласа к обеим частям
модели (2.18) для непрерывной однооткликовой системы,
то можно записать z(s)=h(s)х(s)+v(s). В этом уравнении
z(s), h(s), х(s), v(s) - преобразования Лапласа
соответственно от z(t), h(t), х(t), v(t); h(s) - передаточная
функция непрерывной системы, представляющая собой
преобразование Лапласа от импульсной характеристики.
Преобразование Лапласа имеет вид
∞
∞
∫
+
-js
-
x(s) = x(t)e dt
.
Применяя к обеим частям уравнения (2.18) дискретное
преобразование Фурье, получим z(jw)=h(jw)х(jw)+v(jw),
где z(jw), х(jw), v(jw) - преобразования Фурье
соответственно от отклика, входного сигнала и помехи,
h(jw) - частная характеристика системы, которая есть не
что иное, как преобразование Фурье от импульсной
характеристики. Преобразование Фурье имеет вид
40
∞
∞
∫
+
-jwt
-
x(jw) = x(t)e dt
.
В рассмотренных моделях, использующих
преобразования по Лапласу и Фурье, в роли аргументов
выступают соответствующие параметры преобразований z,
s, j. Все модели линейны по входным сигналам, но, как
правило, нелинейные по параметрам.
2.5. Конечные автоматы
Для моделирования динамических систем,
функционирующих в дискретном времени, применяется
аппарат конечных автоматов [7]. Теория конечных
автоматов и их модели используются при синтезе и анализе
вычислительных устройств, дискретных устройств
автоматики. Конечный автомат функционирует в
дискретные моменты времени t, причем в каждый момент
t
i
автомат находится в одном из возможных состояний z(t
i
),
принадлежащем множеству состояний автомата Z.
Математические модели в виде конечного автомата
получили название F-схем от английского finite automata –
конечный автомат.
В каждый момент t
i
(i=1,2,...) на вход конечного
автомата поступает входной параметр - одна из букв х(t
i
)
входного алфавита Х, а на выходе существует выходной
параметр y(t) - буква выходного алфавита Y.
Автомат формально определен набором
A=<Х,Z,Y,z
0
,ϕ,ψ>,
где Х={х
1
,х
2
,...,х
m
} - множество входных параметров;
Z={z
1
,z
2
,...,z
n
} - множество состояний; Y={y
1
,y
2
,...,y
r
} -
множество выходных параметров. Элементы множества
Х, Z, Y называют входным, внутренним и выходным
