Финаев В.И. Аналитические и имитационные модели
Подождите немного. Документ загружается.


91
- получаем от генератора равномерно распределенных
чисел случайное число
Р
2
(см. блок 5);
- из значения числа
Р
2
находим случайную величину
η=Р
2
(С
i
-С
i-1
), т.е. значение числа Р
2
«приводится» к
величине интервала
[С
i-1
, С
i
] (см. блок 6;
- находим случайную величину
Х, имеющую заданную
плотность распределения вероятностей
f(х), по формуле
(см. блок 7)
η
+
=
−
+
=
=−= 1i1[nP][nP]21[nP]
C)СС(PСX
111
.
Подпрограмма STAT предназначена, как и в алгоритме
метода обратных функций, для набора и обработки
статистических данных о значениях случайной величины
Х.
4.5.3. Использование предельных теорем. Для
имитации случайной величины
Х, имеющей нормальный
закон распределения вероятностей, используют свойство
сходимости независимых величин к нормальному
распределению. Для получения нормального
распределения чисел с параметрами: математическое
ожидание
m
Х
=0, среднеквадратичное отклонение
σ
Х
=1
удобен искусственный прием, основанный на центральной
предельной теореме теории вероятностей. На рис. 4.22
приведен алгоритм получения случайный величин
Х с
применением свойств центральных предельных теорем.
Согласно центральной предельной теореме при
достаточно большом значении
n величина Z может
считаться нормально распределенной с параметрами
∑
k
Zi
i=1
m= M[z]=0
,
∑
i
k
2
Zz
i=1
k
σ = σ =
3
.
Для имитации случайной величины Х в качестве
исходных чисел возьмем
k равномерно распределенных на
отрезке [1,-1] случайных чисел, получаемых из интервала
[0,1] по правилу
z
i
=2Р
i
-1 (см. блоки 5,6).
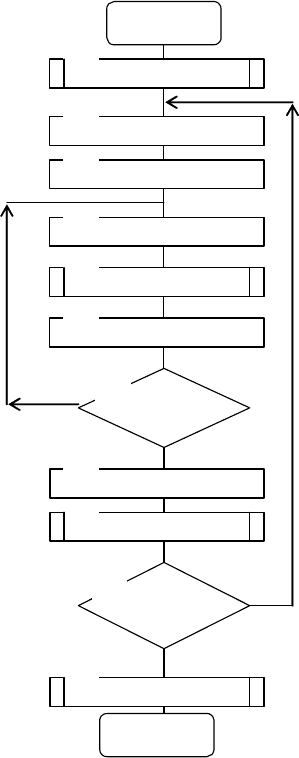
92
I=0, Z=0
3
I=I+1
4
WWOD
1
Начало
N=N+1
2
CEN(P)
5
Z=Z+2(P-1
)
)
6
STAT
10
WIWOD
12
Конец
1
0
N<NZ
11
X=Z×(√3)/(√K)
9
1
0
I<K
7
Рис. 4.22
Сформируем величину
Z согласно следующей формуле
(см. блоки 3 – 7):

93
∑
n
1i
i
zZ
=
=
.
Выполним нормирование величины Z и получим (см.
блок 9)
]
k
1i
1
i
P2[
k
3
z
Z
X
∑
=
−=
σ
=
. (4.11)
Случайная величина Х будет иметь нормальное
распределение с
m
Х
=0,
σ
Х
=1.
Установлено, что при
k>8 формула (4.11) дает хорошие
результаты.
4.6. Имитация марковского процесса
4.6.1. Моделирование дискретной цепи Маркова.
Рассмотрим дискретную цепь Маркова или марковский
процесс с дискретным временем перехода из одного
состояния в другое. Математическая модель дискретной
цепи Маркова задается матрицей вероятностей переходов
||Р
ij
||, имеющей вид
11 12 1n
21 22 2n
ij
n1 n2 nn
P P ... P
P P ... P
P=
... ... ... ...
P P ... P
, (4.12)
где
Р
ij
- вероятность перехода из состояния z
i
в состояние
z
j
в некоторый дискретный момент времени
kΔt (k=1,2,3,...).
Начальное состояние марковского процесса
определяется матрицей-строкой начальных вероятностей
||Р
0
||=|Р
1
(0), Р
2
(0), ..., Р
n
(0)|, где Р
i
(0) - вероятность
нахождения процесса в
z
i
-м состоянии при t=0.
Вероятности перехода
Р
ij
не зависят от времени, т.е.
процесс является однородным.
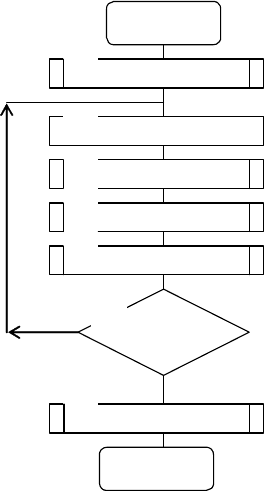
94
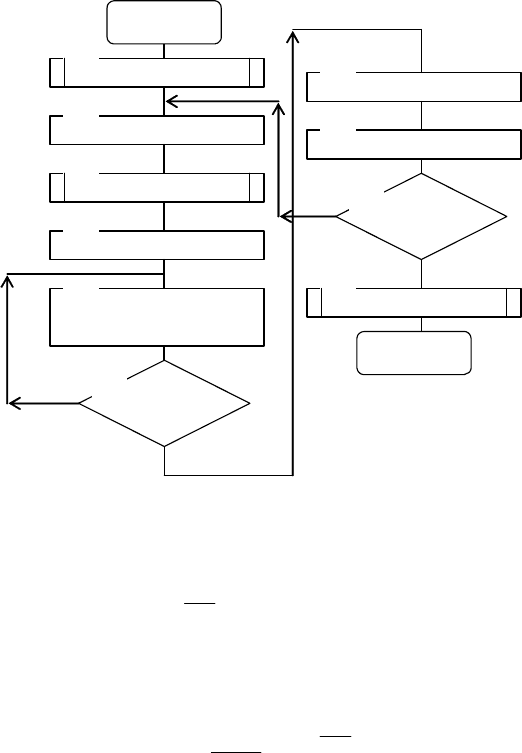
На рис. 4.23 приведен обобщенный алгоритм имитации
дискретной цепи Маркова.
STAT
OPRZ
OPRZ0
3
4
5
WWOD
1
Начало
T=T+1
2
WIWOD
7
Конец
1
0
T<TZ
6
Рис. 4.23
Подпрограммы WWOD и WIWOD реализуют
интерфейсную часть имитационной программы. В
подпрограмме
WWOD осуществляется ввод элементов
массива
Р0[I], в который заносятся вероятности Р
i
(0), и
массива
Р[I,J], в который заносятся вероятности Р
ij
.
Определяется начальный такт моделирования
T=0 и
заданное число тактов моделирования
TZ.
Подпрограмма
OРRZ0 предназначена для определения
начального состояния, а подпрограмма
OРRZ – для
определения состояний в процессе моделирования смены
95
состояний. Подпрограмма
STAT предназначена для набора
статистических данных.
Моделирование марковского процесса основано на
принципе имитации системы случайных событий.
Определяем числовые границы
∑
n
01121 2 n i
i=1
l =0, l =P(0); l =P(0)+P(0),..., l = P(0)=1
.
Исходя из значения случайного числа
Р
0
,
генерированного датчиком случайных чисел, определяется
номер
r начального состояния z
r
(0), для которого будет
справедливо условие
≤
00
r-1 0 r
l<P l
.
Затем датчик случайных чисел вырабатывает случайное
число
Р
1
, которое также сравнивается с границами
∑
n
r0 r1 r1 r2 r1 r2 rn ri
i=1
l = 0, l = P , l = P + P , ..., l = P = 1
.
Путем сравнения устанавливается очередное состояние
и подобным образом осуществляется моделирование
дальше.
Рассмотрим реализации подпрограмм.
На рис. 4.24 приведен алгоритм подпрограммы
OРRZ0.
На рис. 4.25 приведен алгоритм подпрограммы
OРRZ.
На рис. 4.26 приведен алгоритм подпрограммы
STAT.
В алгоритме подпрограммы
OРRZ0 (см. рис. 4.24) в
блоке 1 вырабатывается число
Р датчиком случайных
чисел.
Затем реализуется цикл по переменной
I для сравнения
числа
Р с элементами массива Р0[I]. Для этого введен
идентификатор
А, который в блоке 2 определен А=0.
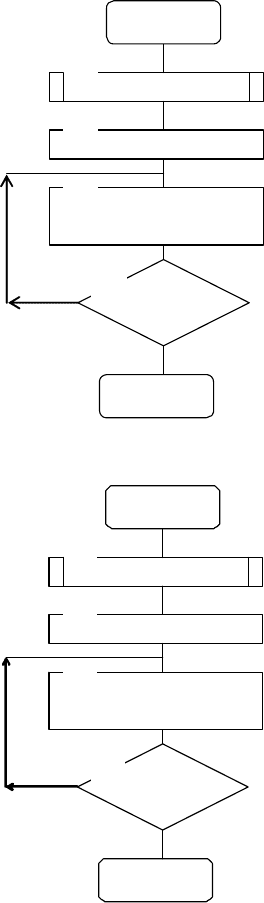
96
СЕN(P)
1
Начало
I=0, A=0
2
I=I+1,
A=A+P0[I]
3
Конец
0
1
P≤A
4
Рис. 4.24
СЕN(P)
1
Начало
J=0, B=0
2
J=J+1,
B=B+P[I,J]
3
Конец
0
1
P≤В
4
Рис. 4.25
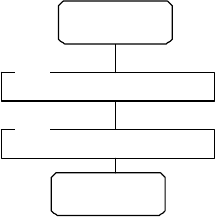
97
K[J]=K[J]+1
1
Начало
I=J
2
Конец
Рис. 4.26
При наращивании переменной I идентификатор А будет
принимать последовательно значения:
I=1, А=Р
1
(0); I=2,
А=Р
1
(0)+Р
2
(0); I=3, А=Р
1
(0)+Р
2
(0)+Р
3
(0); …; I=n,
А=Р
1
(0)+Р
2
(0)+Р
3
(0)+…+Р
n
(0).
При первом же выполнении условия Р≤A считается, что
найден индекс начального состояния
z
i
(0). Таким образом,
выходным параметром подпрограммы
OРRZ0 является
значение индекса
I, при котором выполнено условие
Р≤А=Р
1
(0)+Р
2
(0)+Р
3
(0)+…+Р
i
(0).
В алгоритме подпрограммы
OРRZ (см. рис. 4.25) в
блоке 1 датчиком случайных чисел формируется случайное
число
Р∈[0,1]. Затем реализуется цикл по переменной J для
сравнения числа
Р с элементами массива Р[I,J]. Введен
идентификатор
В. При наращивании переменной J
идентификатор
В будет принимать последовательно
значения:
J=1, А=Р(I,1); J=2, А=Р(I,1)+Р(I,2); …; J=n,
А=Р(I,1)+Р(I,2)+Р(I,3)+…+Р(I,n).
При выполнении условия Р≤B считается, что найдет
индекс состояния
z
j
(T) в текущем такте моделирования T.
Выходным параметром подпрограммы
OРRZ является
значение индекса
J, при котором выполнено условие
Р≤В=Р(I,1)+Р(I,2)+Р(I,3)+…+Р(I,J).
98
В алгоритме подпрограммы
STAT (см. рис. 4.26) в
блоке 1 в счетчиках
K[J] осуществляется подсчет частот
появления событий
z
j
. Затем в блоке 2 осуществляется
присвоение значения индекса
J индексу I, т.е. на
следующем такте моделирования в подпрограмме
OРRZ
будет выполнен анализ
j-й сроки матрицы вероятностей
переходов
||Р
ij
||. Алгоритм имитации дискретной цепи
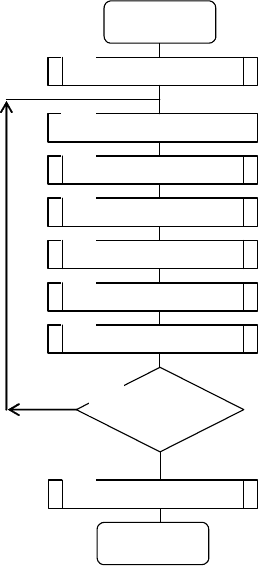
Маркова может быть представлен в более сокращенном
виде, как показано на рис. 4.27. Объединим матрицы
||Р
0
|| и
||Р
ij
|| в обобщенную матрицу вида
nn2n1n
n22221
n1
n0
12
02
11
01
ij
P...PP
............
P...PP
P
P
...
...
P
P
P
P
P =
. (4.13)
В подпрограмме
WWOD осуществляется ввод
элементов массива
Р[I,J], в который заносятся вероятности
Р
ij
, причем
n,oi =
,
n,1j =
. Определяется начальное
значение индекса
I=0, начальный такт моделирования T=0
и заданное число тактов моделирования
TZ.
Так как в первом такте моделирования (
Т=1) I=0, то в
первом такте будет рассматриваться верхняя строка
обобщенной матрицы
||Р
ij
||, т.е. фактически матрицы ||Р
0
||.
В блоке 3 формируется случайное число
Р∈[0,1]. Затем
реализуется цикл по переменной
J для сравнения числа Р с
элементами массива
Р[I,J] при I=0 (см. блоки 4 – 6). При
выполнении условия
Р≤В в соответствующий счетчик K[J]
добавляется единица (см. блок 7). В блоке 8 индексу
I
присваиваются значения индекса
J. Процесс
моделирования продолжается до тех пор, пока не будет
выполнено условие окончания моделирования
T<TZ.
99
СЕN(P)
3
Начало
J=0, B=0
4
J=J+1,
B=B+P[I,J]
5
Конец
0
1
P
≤
В
6
T=T+1
2
K[J]=K[J]+1
7
I=J
8
0
1
T<TZ
9
WWOD
1
WIWOD
10
Рис. 4.27
В счетчиках K[J] после окончания моделирования будут
подсчитаны частоты пребывания марковского процесса в
состояниях
z
j
,
n,1j =
. В подпрограмме WIWOD
осуществляется вывод значений счетчиков
K[J], а также
вывод эмпирических оценок финальных вероятностей
марковского процесса, определяемых по формуле
n1,j ,
TZ
]J[K
v
j
==
.
4.6.2. Моделирование вложенной цепи Маркова. Для
вложенной цепи Маркова, в отличие от дискретной цепи,
переход из состояния в состояние может произойти в
любой случайный момент времени, т.е. время пребывания
марковского процесса в любом состоянии является
100
величиной случайной. Математическая модель
марковского процесса в этом случае определяется:
- распределением вероятностей начального состояния
процесса
Р
i
(0) в момент t
0
;
- матрицей вероятностей переходов
||Р
ij
|| (12);
- матрицей-строкой функций распределения времени
пребывания в состоянии
|A|={A
1
(t), A
2
(t), …, A
n
(t)}, где
A
i
(t) - функция распределения времени пребывания
марковского процесса в состоянии
z
i
.
На рис. 4.28 приведен обобщенный алгоритм имитации
вложенной цепи Маркова.
STAT2
7
OPRTAU
6
STAT1
5
OPRZ
4
OPRZ0
3
T=T+1
2
WWOD
1
Начало
WIWOD
9
Конец
1
0
T<TZ
8
Рис. 4.28
