Финаев В.И. Аналитические и имитационные модели

Подождите немного. Документ загружается.

111

этом случае снижается эффективность имитационного

моделирования.

5.2. Значимость оценки

5.2.1. Статистическая проверка гипотезы

относительно вероятности.

При имитационном

моделировании получают практические (эмпирические)

результаты, которые затем аппроксимируют известными

теоретическими распределениями, т.е. выдвигают гипотезу,

то данное теоретическое распределение аппроксимирует

эмпирическое распределение. Например, необходимо

проверить гипотезу относительно того, что при

выполнении имитационного моделирования частость

=m/N является оценкой вероятности р события.

Пусть проверяется настройка станка на среднюю точку

поля допуска. Проведено 280 независимых испытаний и

интересующее нас событие появилось 151 раз. Модель

появления независимых событий – биноминальное

распределение. Если гипотетическая вероятность события

р=1/2, то математическое ожидание равно

Nр=280(1/2)=140, а среднеквадратичное отклонение

биноминального распределения определится из формулы

××Npq 280

=8,37, где q=1-р – вероятность не

появления события. Надо получить ответ на вопрос: можно

ли считать наблюденную частоту 151 достаточно близкой к

теоретической норме 140, отвечающей гипотезе

р=1/2.

Чтобы получить ответ на заданный вопрос, следует

выбрать границу допустимых при гипотезе отклонений

частот (или частостей) от математического ожидания.

Будет определено критическое отклонение, превышение

которого при выдвинутой гипотезе настолько

112

маловероятно, что его можно считать практически

невозможным. Если превышение критического отклонения

будет наблюдаться, то это указывает на несовместимость

выдвинутой гипотезы с наблюдениями и говорят, что

наблюденная частость значимо отклоняется от

вероятности. Если фактическое отклонение меньше

критической границы, то опыт не противоречит

выдвинутой гипотезе и наблюденное отклонение можно

объяснить случайностью испытаний.

На практике, в соответствии с критерием (5.2), задают

уровень значимости

α, т.е. вероятность практически

невозможных отклонений. Эта вероятность обычно не

превышает значение 0,05. Область больших отклонений,

соответствующую уровню значимости

α, называют

критической областью, а само правило проверки –

критерием значимости. Критическую границу для

отклонений от теоретической нормы можно определить,

пользуясь нормальным приближением к биноминальному

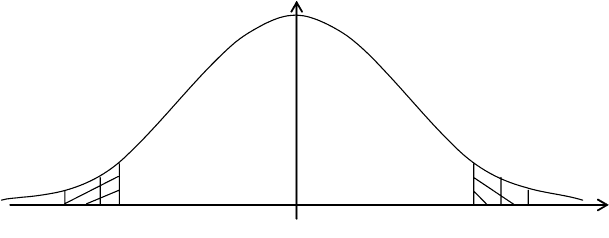
закону. На рис. 5.3 приведены двухсторонние критические

границы для проверки гипотезы

р=1/2.

+1,96-1,96 0

Рис. 5.3

Вероятность 0,95 соответствует при нормированном

нормальном распределении интервалу (-1,96, +1,96) около

центра распределения, т.к. вероятность того, что

113

абсолютная величина нормированного отклонения

превысит значение 1,96, равна 0,05, т.е.

Р(|A|>1,96)=Р(|m-Nр|>1,96σ)≈0,05,

где m – практическая частота.

Уровень значимости 0,01 соответствует границе 2,58,

т.е.

Р(|A|>2,58)=Р(|m-Nр|>2,58σ)≈0,01.

Для рассмотренного выше примера настройки станка на

среднюю точку поля допуска

σ=8,37 и 5% критическая

граница соответствует 1,96

×8,37=16,41, а 1% критическая

граница соответствует 2,58

×8,37=21,59.

Таким образом, область допустимых значений при 5%

критической границы определяется пределами

Nр±1,96σ=140±16,41,

а при области допустимых значений при 1% критической

границы определяется пределами

Nр±2,58σ=140±21,6.

Если выдвинутая гипотеза, что наблюденная частота 151

достаточно близка к теоретической норме 140, отвечающей

вероятности

р=1/2, верна, то отклонение частоты от

теоретической нормы в пяти случаях из 100 может

превышать 16,4, и в одном случае из 100 может превышать

21,6. Так как в рассмотренном примере отклонение

составило 151-140=11, т.е. оно находится в области

допустимых значений, то нет оснований считать гипотезу

р=1/2 противоречащей наблюдениям.

5.2.2. Общая задача проверки гипотез. При наличии

явлений рассеивания признаков случайной величины

требуется провести сравнительную оценку, причем

обоснованный вывод может быть получен путем научно

поставленного анализа статистических данных.

Данные рассматривают как некоторые выборки,

информирующие о поведении случайных величин, и

114

позволяющие делать определенные заключения о законах

распределения этих величин.

Существуют некоторые выборки значений случайной

величины

А. Необходимо сделать заключение о законах

распределения случайной величины

А. Можно сделать

предположение, что тип закона распределения известен

(нормальный, пуассоновский и т.д.), но неизвестны его

параметры, т.е. проверка гипотезы сводится к сравнению

статистических характеристик, оценивающих параметры

выбранных законов распределения.

Для проверки гипотезы согласно критерию выбираются

надлежащие уровни значимости (см. разд. 5.2.1)

α=5%, 2%,

1% и т.д., отвечающие событиям, которые при данном

исследовании считаются практически невозможными.

Затем определяется критическая область (см. рис. 5.3)

данного критерия, вероятность попадания в которую в

точности равна уровню значимости

α, если гипотеза верна.

Значения критерия, лежащие вне критической области,

образуют дополнительную к ней область допустимых

значений (незаштрихованная область на рис. 5.3).

Если

α/100 – уровень значимости, то вероятность

попадания критерия в область допустимых значений при

справедливости выдвинутой гипотезы равна 1-

α/100. Если

значение критерия, вычисленное по произведенным

наблюдениям (опытам), окажется в критической области,

то гипотеза отвергается. Если значение критерия окажется

в области допустимых значений, что наблюденное

значение критерия не противоречит гипотезе.

Чем меньше уровень значимости, тем меньше

вероятность забраковать проверяемую гипотезу, когда она

верна, т.е. совершить ошибку первого рода. С

уменьшением уровня значимости понижается

чувствительность критерия, т.к. расширяется область

допустимых значений и увеличивается вероятность

115

совершения ошибки второго рода, т.е. принятия

проверяемой гипотезы, когда она не верна. Уровень

значимости критерия проверки контролирует лишь ошибки

первого рода и не измеряет степень риска, связанного с

принятием неверной ошибки.

При заданном уровне значимости можно по разному

устанавливать критическую область, гарантирующую этот

уровень. Например, в качестве критерия рассматривается

некоторый показатель, распределенный при проверяемой

гипотезе нормально с плотностью распределения

f(x;a;σ).

В качестве критической области соответствующей уровню

значимости

α=5% можно принять:

- область больших положительных отклонений так, что

Р(t

)=Р(x>a+t

σ)=0,05,

но

)

∞

∫

1q 0q

P(t e dz= -Ф (t )

, (5.11)

тогда из таблицы значений нормированной функции

Лапласа

∫

Ф (z) e dv

определим, что

=1,65;

- область больших отрицательных отклонений

)=Р(x<a-t

σ)=Р(x<a-1,65σ);

- область больших по абсолютной величине отклонений

)=Р(|x-a|>t

σ)=0,05,

определив t из соотношения

)

P(| x - a |> t

116

∞

∫

=1- e dz= -Ф (t )

2π

, (5.12)

так что

=1,96;

- область малых по абсолютной величине отклонений

)=Р(|x-a|>t

σ)=2Ф

(z), (5.13)

так что

≈0,063.

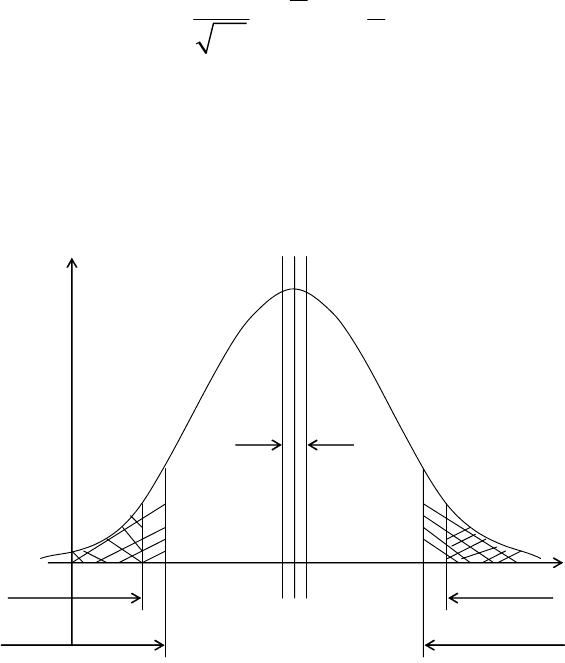
Эти области показаны на рис. 5.4.

3 3

2 1

Значение х критерия

проверки гипотезы

f(x,a,σ

+1,96

-1,96

1 – область больших положительных отклонений;

2 - область больших отрицательных отклонений;

3 - область больших по абсолютной величине отклонений

(состоит из двух половин); 4 - область малых по

абсолютной величине отклонений

Рис. 5.4

5.2.3. Проверка гипотез о законе распределения.

Рассмотренные в предшествующем разделе (см. разд. 5.2.2)

методы проверки предполагали известным закон

117

распределения случайной величины и направлены на

определение параметров распределения. При обработке

результатов имитационного моделирования

(статистических данных) вид закона распределения

является гипотетическим и нуждается в статистической

проверке, т.е. задача о критерии проверки гипотезы по

данным выборки состоит в том, что случайная величина

подчинена закону распределения

Р(х).

Эти критерии, называемые критериями соответствия,

основаны на выборе определенной меры расхождения

между теоретическим и эмпирическим распределениями.

Если такая мера расхождения для рассматриваемого случая

превосходит установленный предел, то гипотеза не

подтверждается.

Рассмотрим наиболее употребительный критерий

(критерий Пирсона). Пусть гипотеза предполагает вид

функции распределения

Р(х). Вся область изменения

случайной величины

Х разбита на конечное число k

множеств

, Δ

, …, Δ

. Если случайная величина Х

непрерывна, то множества

, Δ

, …, Δ

представляют

собой интервалы, а если случайная величина

Х дискретна,

то множества

, Δ

, …, Δ

представляют собой группы

отдельных значений случайной величины

Х. Пусть p

вероятность того, что значения случайной величины

Х при

данном распределении

Р(х) принадлежат интервалу Δ

Объем выборки

N, а m

- число значений случайной

величины

Х в выборке O(x

, x

, …, x

), попавших в

интервал

. Очевидно, что

+ …+p

=1, (5.14)

+ …+m

=N. (5.15)

Если проверяемая гипотеза верна, то

представляет

частоту появления события, имеющего в каждом из

произведенных испытаний вероятность

. В таком случае

118

можно рассматривать как случайную величину,

подчиненную биномиальному закону распределения с

центром в центре в точке

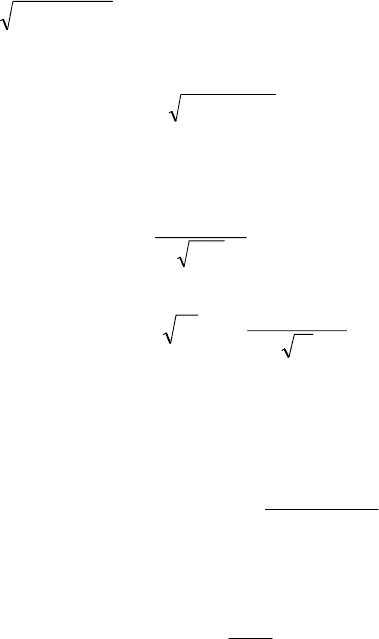
и средним квадратическим

)p1(Np

ii1

−=σ

. Если N достаточно велико, то можно

считать, что частота распределена асимптотически

нормально с центром в центре в точке

и средним

квадратическим

)p1(Np

ii1

−=σ

Если проверяемая гипотеза верна, то можно ожидать,

что в совокупности будут асимптотически нормально

распределены случайные величины

)Npm( −

=ξ

, (i=1,2,…,k), (5.16)

связанные между собой соотношением

∑∑

−

=ξ

)Npm(

, (5.17)

вытекающем из условий (5.14) и (5.15).

В качестве меры расхождения данных выборки

(эмпирических частот)

, m

, …, m

с теоретическими

частотами

, Np

, …, Np

рассмотрим величину

∑∑

−

=ξ=χ

)Npm(

. (5.18)

Для практических приложений можно применять

подобное равенство:

∑

−=χ

. (5.19)

Согласно формуле (5.18) случайная величина

представляет собой сумму квадратов асимптотически

нормально распределенных случайных величин, связанных

линейной зависимостью (5.17).

Из теории вероятностей известна теорема. Если

проверяемая гипотеза верна, то критерий

, определяемый

119

по формуле (5.18), имеет распределение, стремящееся при

N→∞ к распределению χ

с k-1 степенями свободы.

При проведении проверки задают уровень значимости

α% для критерия.

Пусть

обозначает α% предел для закона

распределения

с k-1 степенями свободы. Этот закон

имеет табличное задание и его значения приводятся в

приложениях книг с изложением теории вероятностей.

Если гипотеза верна, то при достаточно большом числе

опытов

N справедливо определение вероятности

100

)(Р

=χ>χ

. (5.20)

После определения случайной величины

по данным

выборки

O(x

, x

, …, x

), будет выполняться одно из

двух условий:

- при

χ>χ

критерий попадает в критическую область

и, следовательно, расхождение выборочных данных с

гипотетическим допущением о законе распределения

случайной величины существенно, гипотеза отвергается;

- при

χ≤χ

несущественно расхождение выборочных

данных с гипотетическим допущением о законе

распределения, гипотеза принимается.

Во втором случае в

α% всех случаев, но неизвестно

каких, гипотеза неверна. Принято считать достаточным

нормальное приближение для практических расчетов, если

≥10 ∀i. Если есть группы со значениями Np

меньшими

10, то рекомендуют соседние группы объединять так,

чтобы новые группы удовлетворяли условию

≥10 ∀i.

Если число степеней свободы

k>30, то

соответствующего значения случайной величины

нельзя

найти в табличном задании закона распределения

. В

120

этом случае применяют следующую приближенную

формулу:

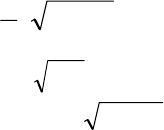
)z12(

+−ν=χ

, (5.21)

основанную на том, что

2χ

оказывается асимптотически

нормальным законом

)1;12(;z(N −ν

, z

2α

- есть 2α%

предел абсолютного уклонения нормальной переменной,

заданный в табличных приложениях книг по теории

вероятностей.

5.3. Формулы и алгоритмы для оценки

результатов моделирования

При реализации моделирующего алгоритма на ЭВМ

вырабатывается информация о состоянии моделируемых

систем, которая представляет собой исходный материал

для определения приближенных искомых величин по

статистическим данным. Желательно так организовать

фиксацию и алгоритмы обработки результатов

моделирования, чтобы статистические оценки для искомых

величин формировались постепенно по ходу

моделирования, без специального запоминания всей

информации о

состояниях системы [8].

Если при моделировании учитываются случайные

факторы, то в качестве оценок для искомых величин

используются средние значения, дисперсия и другие

вероятностные характеристики. В памяти ЭВМ для

формирования оценки желательно занимать как можно

меньше ячеек. При моделировании случайных событий

оценка

Р(A) вероятности Р(A) события A определится по

формуле

Р*(A)=m/N, (5.22)