Финаев В.И. Аналитические и имитационные модели
Подождите немного. Документ загружается.

131
Интересующий интервал
(0,T) разбивается на части с
шагом
Δt. Накапливают значения Х
k
(Δt
i
) реализаций
случайного процесса
Х(t) для фиксированных моментов
времени
Δt
i
. Затем вычисляют оценки для математического
ожидания по формуле
∑
N
iki
k=1
1
MX(Δt)= X (Δt)
N
. (5.29)
Оценки для корреляционной функции B
X
(t
*
,t
**
)
вычисляются по формуле
∑
N
**** *
Xk
k=1
1
B(t,t )= [X(t)-
N-1
*****
k
-X(t )][X (t ) - X(t )]
, (5.30)
где
t
*
и t
**
«пробегают» все значения t. Так при
моделировании при применении формулы (5.30)
необходимо накапливать
N значений X
k
(t
*
) и N значений
X
k
(t
**
). На практике для оценки корреляционной функции
B
X
(t
*
,t
**
) применяют формулу
∑
N
**** * **
X
k=1
1
B (t ,t ) = X (t )X (t ) -
kk
N-1
−
∑∑
NN
***
k=1 k=1
X(t) X(t)
kk
. (5.31)
При применении формулы (5.31) необходимо три
счетчика для подсчета сумм
∑
N
***
k=1
X(t)X(t)
kk
,
∑
N
*
k=1
X(t)
k
,
∑
N
**
k=1
X(t)
k
.
132
6. МОДЕЛИРОВАНИЕ ВЕРОЯТНОСТНЫХ
АВТОМАТОВ
6.1. Аналитическое определение вероятностных
автоматов
6.1.1. Формальное задание и классификация.
Вероятностные автоматы (ВА) относятся к дискретно-
стохастическому классу моделей. Данный тип моделей
служит инструментом изучения динамических систем,
имеющих стохастическую природу функционирования с
дискретным временем. ВА является типичным
представителем таких систем (probabilistic automat) и носит
название P-схемы или P-автомата. В общем виде такой
автомат является потактным преобразователем
информации с памятью, функционирование которого
может
быть описано статистически.
Математический аппарат ВА применим для разработки
методов проектирования дискретных систем, проявляющих
статистически закономерное случайное поведение, для
выяснения возможностей таких систем и обоснования
границ целесообразности их использования, а также при
решении различных задач синтеза. Аппарат ВА
применяется также для моделирования дискретно-
стохастических объектов, у которых подача входных
параметров, изменение
состояния и формирование
выходных параметров осуществляется в дискретные
моменты времени
t
i
(t
0
,t
1
,...,t
i
…). Состояние объекта
определяется через предшествующие состояния и входной
параметр. Выходной параметр определяется через
состояние в данном такте времени, состояние в
предшествующем такте, а также через входной параметр.
133
Для формального описания ВА следует задать
распределение начальных состояний, множество входных
параметров
Х={х
1
,х
2
,...,х
m
}, множество состояний
Z={z
1
,z
2
,...,z
n
}, множество выходных параметров
Y={y
1
,y
2
,...,y
r
}. Элементы множества Х,Z,Y называют
входным, внутренним и выходным алфавитом.
Определение. Вероятностным автоматом называется
математическая схема, которая задается следующим
набором [7,14]:
ВА=<Z,Y,Р
0
,{Р(z
t
,y
t
/z
t-1
,х
t
)}>,
где Р
0
- распределение начальных состояний, Р
0
=||
0
i
P
||,
0
i
P
-
вероятность того, что в такте времени
t
0
автомат будет
находиться в состоянии
z
i
; Р=||Р(z
t
,y
t
/z
t-1
,х
t
)|| -
стохастическая матрица, в которой
Р(z
t
,y
t
/z
t-1
,х
t
)=Р{z(t)=z
t
,
y(t)=y
t
/z(t-1)=z
t-1
, х(t)=х
t
} - условная вероятность того, что в
такте времени
t автомат будет в состоянии z
t
, на выходе
будет иметь параметр
y
t
при условии, что в такте t-1
автомат был в состоянии z
t-1
, а на вход был подан
параметр
х
t
. При моделировании следует определить
функции переходов и выходов. Функцию переходов задают
в виде стохастической матрицы
||Р{z
t
(t)=z(t)/z
t-1
,х
t
}||.
Функция выходов определяет выходные параметры и
задается в виде стохастической матрицы
||Р(y
t
/z
t-1
,х
t
,z
t
)||, в
которой
Р(y
t
/z
t-1
,х
t
,z
t
)=Р{y(t)=y
t
/z(t-1)=z
t-1
,х(t)=х
t
, z(t)=z
t
}.
Определим условную вероятность
Р(y
t
/z
t-1
,х
t
z
t
):
Р(z
t
,y
t
/z
t-1
,х
t
)=Р(z
t
/z
t-1
,х
t
)Р(y
t
/z
t-1
,х
t
,z
t
).
Просуммируем правую и левую части по всем
значениям
y
i
и получим
.)z,x,/zP(y)x,/zP(z)x,/zy,P(z
i
y
tt-1ttt-1tt
i
y
t-1ttt
∑
=
∑
Сумма в правой части равна единице, так как это сумма
вероятностей полной группы событий. Тогда вероятность
Р(y
t
/z
t-1
,х
t
,z
t
) определится формулой

134
∑
=
−
−
−
i
y
t1ttt
t1ttt
tt1tt
)x,z/y,z(P
)x,z/y,z(P
)z,x,z/y(P
.
6.1.2. Классификация ВА. Классификация ВА зависит
от способов определения вероятности
Р(y
t
/z
t-1
,х
t
,z
t
)
функции выходов и вероятности
Р(y
t
/z
t-1
,х
t
) функции
переходов.
Вероятностный автомат называется
автоматом первого
рода
, если функция выходов зависит только от
предшествующего состояния и входного параметра в
данном такте времени:
Р(y
t
/z
t-1
,х
t
,z
t
)=Р(y
t
/z
t-1
,х
t
), (автомат Мили).
Вероятностный автомат называется автоматом второго
рода
, если функция выходов зависит только от состояния и
входного параметра в данном такте времени:
Р(y
t
/z
t-1
,х
t
,z
t
)=Р(y
t
/х
t
,z
t
).
Вероятностный автомат называется правильным, если
функция выходов зависит только от состояния в
предшествующем такте и состояния в текущем такте
времени:
Р(y
t
/z
t-1
,х
t
,z
t
)=Р(y
t
/z
t-1
,z
t
).
Существует правильный ВА первого рода, у которого
Р(y
t
/z
t-1
,х
t
,z
t
)=Р(y
t
/z
t-1
),
и правильный вероятностный автомат второго рода, у
которого
Р(y
t
,z
t-1
,х
t
,z
t
)=Р(y
t
/z
t
), (автомат Мура).
Вероятностный автомат называется автоматом с
детерминированной функцией перехода, если состояние в
каждый такт времени однозначно определяется через
предшествующее состояние и входной параметр:
⎩
⎨
⎧
≠
=
=
−
−
−
).x,z(fz ,0
),x,z(fz ,1
)x,z/z(P
t1tt
t1tt
t1tt
135
Вероятностный автомат будет называться
автоматом с
детерминированной функцией выходов
, если выходной
параметр однозначно задается через предшествующее и
текущее состояние и входной параметр:
⎩
⎨
⎧
ϕ≠
ϕ=
=
−
−
−
).z,x,z(y ,0
),z,x,z(y ,1
)z,x,z/y(P
tt1tt
tt1tt
tt1tt
Вероятностный автомат первого рода с
детерминированной функцией переходов называется
автоматом со случайными реакциями.
Вероятностный автомат первого рода с
детерминированной функцией выходов называется
марковским.
Правильный ВА второго рода с детерминированной
функцией выходов называется
автоматом с отмеченными
состояниями
. Каждому состоянию соответствует свой
входной параметр. Причем, если у этого ВА стохастическое
отображение элементов множества
Z в элементы
множества
Y задается взаимно однозначно, то ВА
называется
абстрактным и для него достаточно
рассматривать алфавит внутренних состояний.
Абстрактный ВА задается в виде набора
ВА=<Х,Z,Р
0
{Р(z
t
/z
t-1
,х
t
}>.
Если мощность множества Z равна единице, то такой
автомат называется
автоматом без памяти.
Если мощность множества
Х равна единице, то такой
автомат называется автономным.
Автономный абстрактный ВА называется
дискретной цепью Маркова
и задается в следующем
виде:
ВА=<Z,Р
0
{Р(z
t
/z
t-1
)}>.
136
6.2. Табличное задание функций переходов и
выходов
Задание условных вероятностных мер Р(z
t
,y
t
/z
t-1
,х
t
)
возможно как задание стохастического отображения
Z×ХÆZ×Y табличным способом. В табл. 6.1 приведен вид
совместного задания функций переходов и выходов.
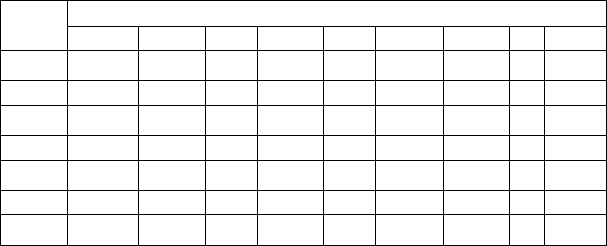
Таблица 6.1
Совместное задание функций переходов и выходов
Z×Y Z×Х
z
1
y
1
z
1
y
2
… z
1
y
r
… z
n
y
1
z
n
y
2
…z
n
y
r
z
1
х
1
11
11
P
11
12
P
…
11
r1
P
…
11
1n
P
11
2n
P
…
11
nr
P
… … … … … … … … … …
z
1
х
m
m1
11
P
m1
12
P
…
m1
r1
P
…
m1
1n
P
m1
2n
P
…
m1
nr
P
… … … … … … … … …
z
n
х
1
1n
11
P
1n
12
P
…
1n
r1
P
…
1n
1n
P
1n
2n
P
…
1n
nr
P
… … … … … … … … … …
z
n
х
m
nm
11
P
nm
12
P
…
nm
r1
P
…
nm
1n
P
nm
2n
P
…
nm
nr
P
Элементы каждой строки табл. 6.1 должны быть
нормированы, т.е.
1P
n
1i
r
1j
pk
ij
=
∑∑
==
.
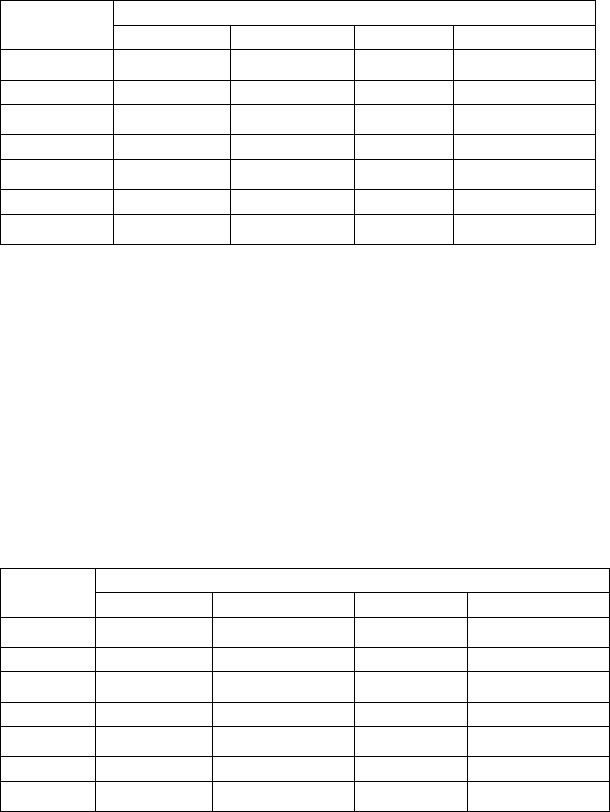
Функция переходов может быть представлена как
стохастическое отображение элементов множества
Z×Х в
элементы множества
Z. В табл. 6.2 приведен общий вид
задания функции переходов. Элементы каждой строки
табл. 6.2 также отвечают условию нормирования, т.е.
.1P
n
1i
pk
i
=
∑
=
Таблица 6.2
Задание функции переходов
137
Z
Z×Х
z
1
z
2
… z
n
z
1
х
1
11
1
P
11
2
P
…
11
n
P
… … … … …
z
1
х
m
m1
1
P
m1
2
P
…
m1
n
P
… … … … …
z
n
х
1
1n
1
P
1n
2
P
…
1n
n
P
… … … … …
z
n
х
m
nm
1
P
nm
2
P
…
nm
n
P
Функция выходов может быть представлена как
стохастическое отображение элементов множества
Z×Х×Z
в элементы множества
Y.
В табл. 6.3 приведен общий вид задания функции
выходов. Элементы каждой строки табл. 6.3 отвечают
условию нормирования, т.е.
∑
r
ρkl
j
j=1
P=1
.
Таблица 6.3
Задание функции выходов
Y
Z×Х×Z
y
1
y
2
… y
n
z
1
х
1
z
1
111
1
P
111
2
P
…
111
n
P
… … … … …
z
n
х
1
z
n
n1n
1
P
n1n
2
P
…
n1n
n
P
… … … … …
z
n
х
m
z
1
1nm
1
P
1nm
2
P
…
1nm
n
P
… … … … …
z
n
х
m
z
n
nmn
1
P
nmn
2
P
…
nmn
n
P
При применении аппарата вероятностных автоматов для
решения задач моделирования сложных систем
необходимо определить множества входных параметров,
состояний и выходных параметров, определить функции
138
переходов и выходов. Следующим этапом в моделировании
будет идентификация значений вероятностей функций
переходов и выходов и проверка адекватности найденной
модели.
6.3. Имитационное моделирование
вероятностных автоматов
Для имитации процесса функционирования ВА
необходимо задать:
- такты моделирования
T, а также цикл по тактам
моделирования от нуля до заданного числа тактов
моделирования
TZ;
- закон (правило) появления (генерации) входных
параметров
х
t
∈Х на входе ВА;
- модель функции переходов
||Р{z
t
(t)=z(t)/z
t-1
,х
t
}||;
- модель функции выходов
||Р(y
t
/z
t-1
,х
t
,z
t
)||;
- определить счетчики для набора статистических
данных.
Закон генерации входных параметров может быть задан
в детерминированном виде и в виде стохастического
распределения.
Детерминированный закон определяет
детерминированные правила появления входного
параметра
х в такте моделирования T.
Стохастический закон появления входного параметра
х в
такте моделирования
T представляет собой распределение
вероятностей
W=|w
1,
w
2,
…
,
w
m
|, где w
i
- вероятность
появления входного параметра
х
i
.
Структурная схема алгоритма имитационной модели ВА
при стохастическом законе появления входного параметра
х приведена на рис. 6.1.
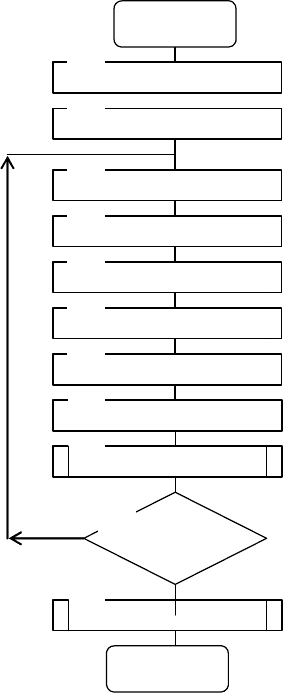
139
0
Начало
WIWOD
11
Конец
1
T<TZ
10
STATY
9
OPRV
8
STATZ
7
OPRZ
6
STATX
5
GENX
4
T=T+1
3
GENZ0
2
WWOD
1
Рис. 6.1
Подпрограмма WWOD, как интерфейсная часть,
предназначена для ввода исходных данных для
моделирования, определенных выше. Подпрограмма
WIWOD составляет также интерфейсную часть
имитационной модели и предназначена для вывода
результатов моделирования. В подпрограмме
GENZ0,
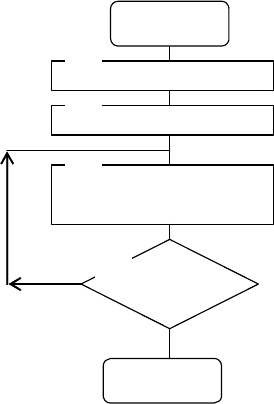
140
исходя из значений вероятностей
00 0
12 n
P , P ,...,P ,
генерируется в схеме случайных событий (см. разд. 4.4)
начальное состояние
z(t
0
) ВА. Алгоритм подпрограммы
GENZ0 приведен на рис. 6.2.
Начало
J=0, A=0
2
J=J+1,
A=A+W[J]
3
Конец
0
1
P≤A
4
СЕN(P)
1
Рис. 6.2
Работает алгоритм подпрограммы GENZ0 следующим
образом. В блоке 1 вырабатывается датчиком случайных
чисел число
Р, равновероятно распределенное на отрезке
[0,1]. В блоках 2 – 4 число Р сравнивается со значениями
0
1
P ,
00
12
P+P,
000
123
P+P+P и т.д. При первом выполнении
условия
Р<
00 0
12 j
P + P + ... + P
считается, что начальным состоянием ВА является
состояние
z
j
. Выходным параметром подпрограммы
GENZ0 является параметр J – индекс состояния z
j
.
