Федосеев В.В. и др. Экономико-математические методы и прикладные модели

Подождите немного. Документ загружается.

Модели прогнозирования экономических процессов 221

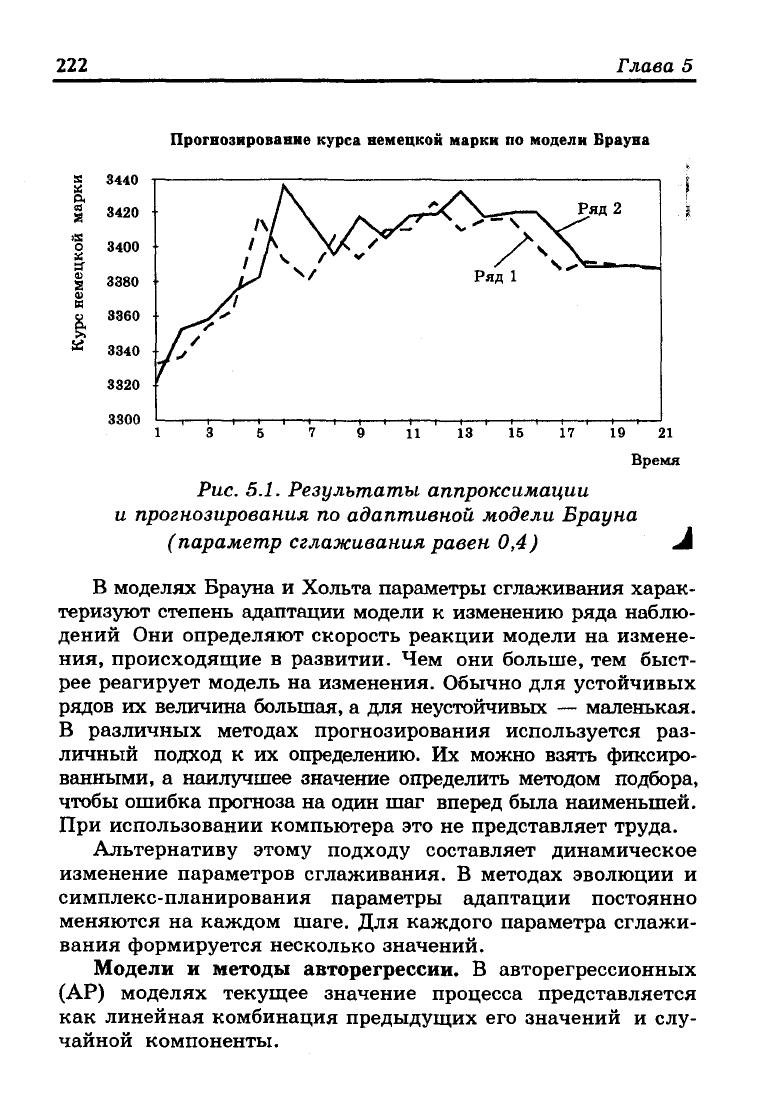
На рис. 5.1 представлены результаты аппроксимации и

прогнозирования по этой модели. Ряд 1 соответствует фак-

тическим данным, ряд 2 — расчетным данным по модели

Брауна, при этом указаны точечные прогнозы на два шага

вперед. Интервальные прогнозы можно получить, используя

приведенные в табл. 5.7 значения £7(1) и 17(2).

Таблица

5.7.

Оценка параметров модели Брауна

Y(t)

3333

3337

3354

3364

3418

3392

3380

3406

3394

3409

3410

3425

3409

3415

3416

3402

3387

3391

3390

3302,1

3331,2

3339,5

3354,7

3365,4

3412,3

3398,9

3385,5

3404,4

3397,5

3408,5

3411,2

3424,0

3412,8

3415,4

3416,6

3404,9

3390,0

3390,5

3389,8

19,7

21,5

19,0

18,3

16,8

22,5

15,7

10,2

11,8

8,3

8,8

7,6

8,6

4,8

4,4

3,8

0,9

-2,2

-1,7

-1,5

Y„(t)

3321,8

3352,7

3358,5

3373,0

3382,3

3434,8

3414,5

3395,7

3416,2

3405,8

3417,3

3418,8

3432,6

3417,6

3419,8

3420,4

3405,8

3387,9

3388,8

3388,3

3386,9

e(t)

11,2

-15,7

-4,5

-9,0

35,7

-42,8

-34,5

10,3

-22,2

3,2

-7,3

6,2

-23,6

-2,6

-3,8

-18,4

-18,8

3,1

1,2

17(1) =

36,31,

£7(2) = 36,86.

222

Глава 5

Прогнозирование курса немецкой марки по модели Брауна

Рис. 5.1. Результаты аппроксимации

и прогнозирования по адаптивной модели Брауна

(параметр сглаживания равен 0,4) А

В моделях Брауна и Хольта параметры сглаживания харак-

теризуют степень адаптации модели к изменению ряда наблю-

дений Они определяют скорость реакции модели на измене-

ния, происходящие в развитии. Чем они больше, тем быст-

рее реагирует модель на изменения. Обычно для устойчивых

рядов их величина большая, а для неустойчивых — маленькая.

В различных методах прогнозирования используется раз-

личный подход к их определению. Их можно взять фиксиро-

ванными, а наилучшее значение определить методом подбора,

чтобы ошибка прогноза на один шаг вперед была наименьшей.

При использовании компьютера это не представляет труда.

Альтернативу этому подходу составляет динамическое

изменение параметров сглаживания. В методах эволюции и

симплекс-планирования параметры адаптации постоянно

меняются на каждом шаге. Для каждого параметра сглажи-

вания формируется несколько значений.

Модели и методы авторегрессии. В авторегрессионных

(АР) моделях текущее значение процесса представляется

как линейная комбинация предыдущих его значений и слу-

чайной компоненты.

Модели прогнозирования экономических процессов 223

Идентификация АР(р) модели состоит в определении ее

порядка р. Одной из предпосылок построения модели этого

типа является применение их к стационарному процессу.

Поэтому в более широком смысле идентификация модели

включает также выбор способа трансформации исходного

ряда наблюдений, как правило, имеющего некоторую тен-

денцию, в стационарный (или близкий к нему) ряд. Один

из наиболее распространенных способов решения этой про-

блемы — последовательное взятие разностей, т.е. переход от

исходного ряда к ряду первых, а затем и вторых разностей.

«Чистые» авторегрессионные процессы имеют плавно за-

тухающую автокорреляционную функцию (АКФ). В этом

случае в качестве порядка модели выбирается лаг, после ко-

торого все частные автокорреляционные функции (ЧАКФ)

имеют незначительную величину. Однако на практике ред-

ко встречаются процессы, которые легко было бы идентифи-

цировать. Поэтому порядок модели обычно определяется ме-

тодом проб из нескольких альтернатив. В число кандидатов

включаются модели, у которых порядок соответствует ЧАКФ,

превышающей стандартное отклонение 1/N. При обработке

разностных рядов иногда ориентируются на АКФ, выбирая

модели, у которых порядок соответствует максимальному ее

значению, при условии, что оно превышает стандартное от-

клонение.

Ряды без тенденции, как правило, не представляют инте-

реса для экономистов. АР-модели вообще не предназначены

для описания процессов с тенденцией, однако они хорошо

описывают колебания, что весьма важно для отображения

развития неустойчивых показателей.

Чтобы сделать возможным применение АР-моделей к

процессам с тенденцией, на первом этапе формируют ста-

ционарный ряд, т. е. исключают тенденцию путем перехода

от исходного временного ряда к ряду Z(t) (t = 1,2, ..., N-d)

первых или вторых разностей (d = 1 или 2).

Z(t) = Y(t), t =

1,2,...,JV

при d = 0;

Z(t) = Y(t+1) - Y(t), t = l,2,...,iV-l, d = 1;

Z(t) = Z(t+1) - Z(t), t = l,2,...,JV-2, d = 2.

224

Глава 5

Например, ряд первых разностей формируется как ряд

приростов, т. е. последовательным вычитанием двух соседних

уровней. С учетом этого АР(р) — модель порядка р имеет вид:

Z(t) =Ло +Al-Z(t - 1) + A2-Z(t - 2) + ... + Ap-Z(t -p).

Параметры этой модели вычисляются по МНК с учетом

сложности модели либо методом адаптивной фильтрации

(МАФ). В обоих случаях необходимо предварительно иден-

тифицировать модель, т. е. правильно определить порядок

разностного ряда d и порядок модели р.

Простейшим способом определения наиболее подходящего

разностного ряда является вычисление для каждого ряда

(d = 0,1,2) его дисперсии, т. е. усредненной суммы квадратов

расхождений его уровней со средним значением Z

. Для

дальнейшей обработки выбирается ряд, у которого величина

этого показателя минимальна.

Для идентификации порядка модели обычно используется

автокорреляционная функция, значения которой определя-

ются по формуле:

r(m) = Z{(Z(t) - Z

)(Z(t - т) -

)}

/£(Z(*) - Z

)

где га — количество уровней стационарного ряда (га = N-d);

т — номер коэффициента автокорреляции (т < га/3).

В качестве порядка модели принимается номер коэффи-

циента автокорреляции г(т), имеющего максимальную ве-

личину. Следовательно, в модели используются р уровней,

которые оказывают на текущий уровень наибольшее влияние.

В соответствии с МНК формируется система из р уравнений,

которая в компактной форме имеет вид:

( Р \

Y,Z(t-i)

ZW-XAjW-j) =0.

( = p+l V ; = 1 J

Например, для р = 2 система принимает вид:

А, X z(t -1)

X z(t - i)Z(t -2)

^г(г- i)Z(t),

A^Z(t

- l)Z(t -2)

A^Zit - 2)

= £Z(f - 2)Z(t).

Модели прогнозирования экономических процессов 225

В ней суммирование проводится по f в пределах от 3 до

n = N - d.

Решив эту систему уравнений, получают числовое значе-

ние

А\,А2,

—

,А

. Оценка свободного члена получается из со-

отношения:

Ао = Z

[1 - (Ai +A

+ ... + А

)].

На основе построенной модели вычисляют прогнозное

значение разностного ряда Z(n+k) на k шагов вперед, а от

него переходят к прогнозной оценке исходного ряда.

Так, для d = 1 имеем:

Y(JV+1) = Y(N) + Z(n+1) при k = 1,

Y(N+2) = Y(N+1) + Z(n+2) при k = 2.

Следовательно, прогнозные оценки базируются как на

фактических, так и на полученных прогнозных уровнях ряда.

Доверительный интервал прогноза рассчитывается на основе

точечного прогноза:

верхняя граница прогноза = Z(N+k) + U(k),

нижняя граница прогноза = Z(N+k) - U(k).

Величина U(k) рассчитывается по формуле:

где Sg — СКО, вычисленное с учетом сложности АР(р)-#

модели; t

— коэффициент, соответствующий табличному

значению статистики Стьюдента с выбранным уровнем зна-

чимости а; коэффициент под квадратным корнем рассчиты-

вается рекуррентно, причем при / = 0 величина С(0) = 1,

а при ;>0

СО) - jA

C(j - 1) + A

C(j - 2)+...+A

(j - р).

В методе адаптивной фильтрации используется АР(р)-модель

без свободного члена. Ее параметры корректируются на ;'-й ите-

рации в каждый момент времени t следующим образом:

226

Глава 5

A{t,i) = A(t-l,i) - 2we(t)Z(t-i),

где A(t,i) и A(t-l,i) — векторы новых и старых значений

параметров (весов) модели;

ш — константа обучения, определяющая скорость адаптации

параметров модели (w>0);

e(t) — ошибка прогнозирования уровня Y(t).

Алгоритм построения модели прогнозирования состоит в

следующем. На первой итерации (у = 1) на основе начально-

го набора весов и первых р уровней ряда вычисляется Z

(t)

и его расхождение с фактическим уровнем, т.е. e(t)=Z(t)-

{t),

t=p+l. Подставляя величину ошибки в уравнение кор-

ректировки весов, получают новый набор весов для следую-

щего момента времени t = р+2. Далее эта процедура повто-

ряется для следующих р-наборов Z(t-i) (i=l,..., p;

t=p+2,...,n),

каждый из которых образован из предыдущего

исключением первого и добавлением одного нового уровня

ряда. Если на итерации j оптимальные веса не получены, то

на следующей итерации надо вернуться к первому набору

уровней ряда Z(p+l-i)

(£=1,...,

p), но уже с новыми началь-

ными весами, взятыми от предыдущей итерации.

Определение начальных весов осуществляется путем ре-

шения уравнения Юла—Уокера, составленного на основе ко-

эффициентов автокорреляции. Процедура корректировки

параметров заканчивается, когда среднеквадратическая

ошибка перестает существенно убывать или при достижении

заданного максимального количества итераций.

Пример 4. Рассмотрим построение прогноза на основе мо-

делей авторегрессии. Ниже в табл. 5.8 и 5.9 приведены рас-

четы построения прогноза курса немецкой марки, выпол-

ненные с использованием программы ОЛИМП; при этом в

качестве лучшей модели из всего класса адаптивных моде-

лей, реализованных в программе, выбрана авторегрессион-

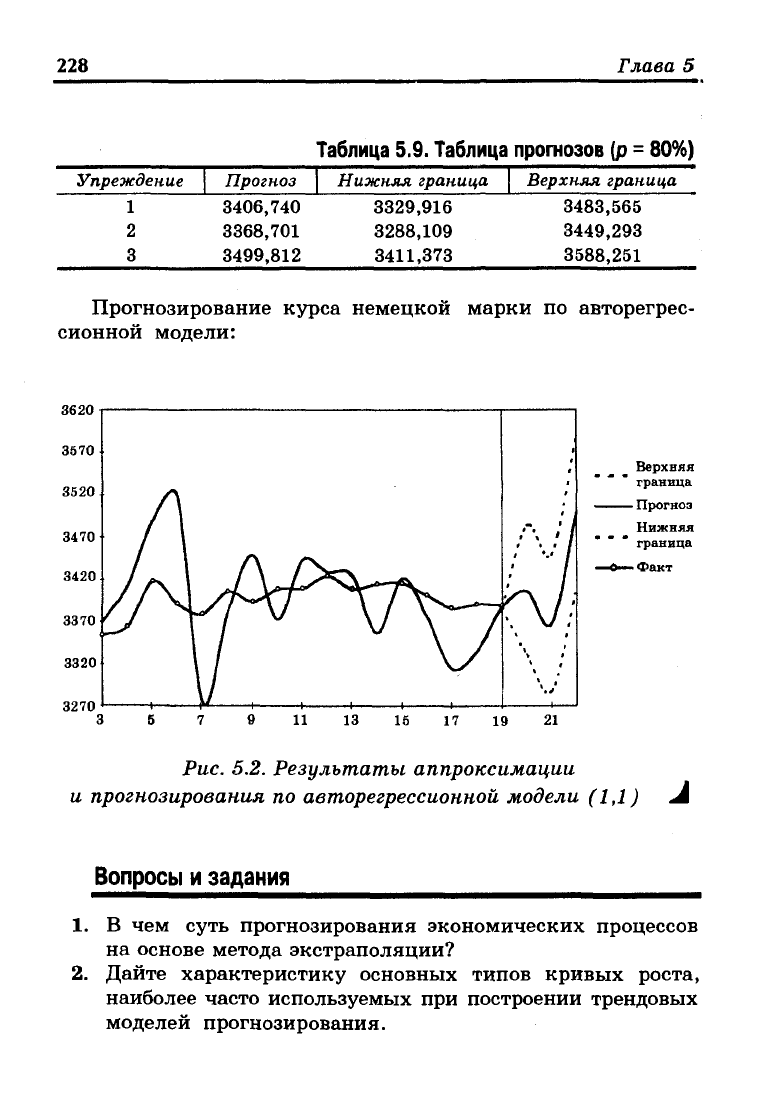
ная модель. На рис. 5.2 представлены результаты аппрокси-

мации и прогнозирования по этой модели.

Модели прогнозирования экономических процессов 227

Таблица 5.8. Модель временного ряда «Немецкая марка»

Лучшая модель АР(1,1)

Модель

АР(1Д)

3,088

-0,248

Таблица остатков

Номер Факт

Расчет

Ошибка

абсолютная

Ошибка

относительная

3354,000

3364,000

3418,000

3392,000

3380,000

3406,000

3394,000

3409,000

3410,000

3425,000

3409,000

3415,000

3416,000

3402,000

3387,000

3391,000

3390,000

3369,699

3412,840

3489,226

3519,090

3274,064

3381,294

3448,631

3373,294

3443,665

3429,435

3425,665

3357,942

3421,874

3377,435

3315,118

3335,030

3387,699

-15,699

-48,840

-71,226

-127,090

105,936

24,706

-54,631

35,706

-33,665

-4,435

-16,665

57,058

-5,874

24,565

71,882

55,970

2,301

-0,468

-1,452

-2,084

-3,747

3,134

0,725

-1,610

1,047

-0,987

-0,129

-0,489

1,671

-0,172

0,722

2,122

1,651

0,068

Характеристики остатков

Характеристика

Значение

Среднее значение

Дисперсия

Средний модуль остатков

Относительная ошибка

Критерий Дарбина-Уотсона

Коэффициент детерминации

F-значение

(п

—

=15)

Уравнение значимо с вероятностью

0,000

3151,663

44,485

1,310

1,901

1,000

54932,906

0,95

228

Глава 5

Упреждение

Прогноз

3406,740

3368,701

3499,812

Таблица 5.9. Таблица прогнозов (р

80%)

Нижняя граница Верхняя граница

3329,916 3483,565

3288,109 3449,293

3411,373 3588,251

Прогнозирование курса немецкой марки по авторегрес-

сионной модели:

Верхняя

граница

- Прогноз

Нижняя

граница

• Факт

Рис. 5.2. Результаты аппроксимации

и прогнозирования по авторегрессионной модели (1,1) А

Вопросы и задания

В чем суть прогнозирования экономических процессов

на основе метода экстраполяции?

Дайте характеристику основных типов кривых роста,

наиболее часто используемых при построении трендовых

моделей прогнозирования.

Модели прогнозирования экономических процессов 229

Укажите методы предварительного выбора кривой рос-

та. Как находятся параметры этих кривых?

Каким образом проводится оценка адекватности трен-

довых моделей? Какие статистические критерии при

этом используются?

Назовите статистические критерии оценки точности

моделей прогнозирования в экономике.

6. Перечислите основные этапы прогнозирования экономи-

ческой динамики на основе одномерных временных ря-

дов с использованием трендовых моделей.

Опишите порядок получения точечного и интервального

прогноза экономического показателя ?а основе трендовых

моделей. От каких факторов зависит ширина довери-

тельного интервала прогноза?

8. Поясните суть адаптивных методов прогнозирования.

Какие типы адаптивных моделей вы знаете?

9. Укажите этапы построения и использования адаптивной

модели Брауна. Как влияет параметр сглаживания на

скорость адаптации моделей этого типа к изменениям

в прогнозируемом процессе?

10.

Дайте краткую характеристику авторегрессионных

моделей прогнозирования. Для каких экономических

процессов применимы методы авторегрессии?

Упражнения

Временной ряд задан в таблице:

* 1

3 4 5 6

7 8 9 10

43 47 50 48 54 57 61 59 65 62

Сделайте предварительный выбор наилучшей кривой роста:

а) методом конечных разностей (Тинтнера);

б) методом характеристик прироста.

Для ряда, приведенного в упр. 1, построить линейную

модель y

—

+ a\t, определив ее параметры методом наи-

меньших квадратов.

230

Глава 5

Для временного ряда из упр. 1 построить адаптивную

модель Брауна с параметром сглаживания а = 0,4 и а = 0,7;

выбрать наилучшую модель Брауна y(k) =

+ a\k, где k —

период упреждения (количество шагов вперед).

Оценить адекватность моделей, построенных в упр. 2 и

на основе исследования:

а) близости математического ожидания остаточной ком-

поненты нулю; критическое значение статистики Стьюдента

принять t

= 1,09 (для доверительной вероятности 0,70);

б) случайности отклонений остаточной компоненты по

критерию пиков (поворотных точек); расчеты выполнить на

основе соотношения (5.9);

в) независимости (отсутствия автокорреляции) уровней ря-

да остатков либо по критерию Дарбина—Уотсона (в качестве

критических используйте уровни dj = 1,08 и d

1,36),

либо

по первому коэффициенту автокорреляции (критический

уровень принять равным г\ = 0,36);

г) нормальности закона распределения остаточной ком-

поненты на основе .RS-критерия (в качестве критических

уровней принять интервал 2,7-3,7).

Оценить точность моделей, построенных в упр. 2 и 3,

используя показатели среднего квадратического отклонения

и средней относительной ошибки аппроксимации.

6. На основе сравнительного анализа адекватности и точ-

ности моделей по результатам упр. 4 и 5 выбрать лучшую

модель, по которой построить точечный и интервальный

прогнозы на два шага вперед (t

1,09).

Результаты про-

гнозирования отразить графически.