Fattorini H.O., Kerber A. The Cauchy Problem

Подождите немного. Документ загружается.

6.1. Improperly Posed Problems

347

the deterministic point of view and to obtain information by other means

(e.g., by probabilistic arguments). This was known to the creators of

probability theory and was explicitly stated by Poincare almost a century

ago. In the words of Hadamard [1923: 1, p. 38]. "But in any concrete

application, "known," of course, signifies "known with a certain approxi-

mation," all kinds of errors being possible, provided that their magnitude

remains smaller than a certain quantity; and, on the other hand, we have

seen that the mere replacing of the value zero for u, by the (however small)

value (15) [here Hadamard refers to the "initial velocity" u, in the Cauchy

problem for the Laplace equation] changes the solution not by very small

but by very great quantities. Everything takes place, physically speaking, as

if the knowledge of Cauchy's data would not determine the unknown

function."

"This shows how very differently things behave in this case and in

those that correspond to physical questions. If a physical phenomenon were

to be dependent on such an analytical problem as Cauchy's for p 2 u = 0, it

would appear to us as being governed by pure chance (which, since

Poincare, has been known to consist precisely in such a discontinuity in

determinism) and not obeying any law whatever."' Earlier in [1923: 1] (p.

32) Hadamard concludes: "But it is remarkable, on the other hand, that a

sure guide is found in physical interpretation: an analytical problem always

being correctly set, in our use of the phrase, when it is the translation of

some mechanical or physical question; and we have seen this to be the case

for Cauchy's problem in the instances quoted in the first place."

"On the contrary, none of the physical problems connected with

p 2 u = 0 is formulated analytically in Cauchy's way." 2

A look at the vast amount of literature produced during the last two

decades on deterministic treatment of improperly posed problems (including

numerical schemes for the computation of solutions) would appear to prove

Hadamard's dictum wrong. However, it may be said to remain true in the

sense that, many times, a physical phenomenon appears to be improperly

posed not due to its intrinsic character but to unjustified use of the model

that describes it; for instance, the model may have " unphysical" solutions

in addition to the ones representing actual trajectories of the system, bounds

and constraints implicit in the phenomenon may be ignored in the model,

the initial or boundary value problems imposed on the equation may be

incorrect translations of physical requirements, and so on. We present in

this section a number of examples where seemingly improperly posed

problems result from neglecting physical considerations, but where the

"discontinuity in determinism" can be removed by careful examination of

'From J. Hadamard, Lectures on Cauchy's Problem in Linear Partial Differential

Equations (New Haven: Yale University Press, 1923).

2Ibid.

348

Some Improperly Posed Cauchy Problems

the relations between model and phenomenon. These examples motivate the

theory in the rest of the chapter.

6.1.1 Example. Solutions of the heat equation that cease to exist in finite

time. Consider the heat-diffusion equation

ut = KuXX

(6.1.1)

in the whole line - oo < x < oo. We can arrange an abstract Cauchy

problem for it as follows. Let a > 0, E = Ca221 where Ca,

is the space of all

functions u defined in - oo < x < oo and such that

(lull =

sup

l u(x)l (l + lxl)exp(- alxla) <00.

-00<X<00

Obviously, each Ca

is a Banach space. The operator A is defined by

Au = u" with domain D(A) consisting of all twice differentiable u in E with

u" E E. Let 0 < b < a,

u(x t) = 1

ebX2/(1 -4bKt)

Then the E-valued function t -p u(., t) is a solution of

u'(t) = Au(t) (6.1.2)

in - oo < t < T= (a - b)/4abK with initial condition u(x,0) = ebXZ, but it

ceases to exist3 for t = T. This type of solutions of an abstract differential

equation (6.1.2) have been called explosive solutions by Hille [1953: 3]. If

(6.1.1) is to be taken as a model for, say, a heat propagation or diffusion

process, the existence of explosive solutions is embarrassing since it would

imply that certain heat or diffusion processes "blow themselves up" without

any obvious cause (such as internal chemical reactions). However, an actual

temperature distribution must be bounded, while the integral of a density

(the total amount of matter) is finite. Both conditions are violated by the

elements of the space E. We must then conclude that the misbehavior of the

model is due to inadequate choice of the "state space" E; indeed, it is well

known that explosive solutions of (6.1.1) do not exist if we take E =

BC(- oo, oo) (the space of bounded continuous functions endowed with the

supremum norm) or E = L'(- oo, oo). In fact, in both these cases the

solution corresponding to the initial condition u(x) is given by the

Weierstrass formula

u(x t) =

roo

e-(X-E)Z/4Ktu(E)

2 7TKt " - o0

for all t > 0 (for uniqueness in both cases see John [1978: 1, Ch. 7], where

the m-dimensional case is also covered).

3 That is, liml l u (t )I I = oo as t

T -

6.1. Improperly Posed Problems

349

6.1.2 Example. Nonuniqueness for the heat equation. Let g(t) be infinitely

differentiable in - oo < t < oo. The function

u(x,

t) - 0

(2n()I)

X2n

is a formal solution of (6.1.1) (with K =1\). If

g(t)-

eXp(-t-2)

(t>0)

0 (t < 0),

(6.1.3)

the series given by (6.1.3) is uniformly convergent (together with all its

derivatives) on compact subsets of the (x, t)-plane; moreover, there exists a

constant 0, 0 < 0 < 1 such that

u(x,t)I<exp

Bt 2t2

(-oo<x<00,t>0). (6.1.4)

(For this result and related information see John [1978: 1, p. 172].) We note

next that

2 4

Ot -

(- 00 < X < 00, t > 0).

2t2 202

Let E = Co4 4 with a > 1/202, the operator A defined as in the previous

example. It is not difficult to see that the function t - u(-; t) is infinitely

differentiable in the sense of the norm of E and solves (6.1.2) for all t. Since

u(0) = 0, solutions of this equation are not uniquely determined by their

initial data. This undesirable behavior of (6.1.1) as a model can again be

traced to the unphysical nature of the space E in this Example.

It is remarkable that lack of uniqueness for solutions of (6.1.1) is also

related to the neglect of the condition u >, 0, which must hold for a density

or an absolute temperature. In fact, it was shown by Widder [1944: 1] (see

also [1975: 1, p. 157]) that an arbitrary solution of (6.1.1) in - oo < x < oo,

t > 0 that vanishes for t = 0 and is nonnegative everywhere must be identi-

cally zero.

We note finally that all the anomalies related to nonuniqueness are

consequence of the unavoidable fact that the line t = 0, carrier of the initial

data, is a characteristic of the equation (6.1.1). For general results on

nonuniqueness in characteristic Cauchy problems see Hormander [1969: 1,

Ch. 5].

For an abstract differential equation u'(t) = Au(t), nonuniqueness,

as well as existence of explosive solutions, are closely related to certain

spectral properties of A. See Hille-Phillips [1957: 1, p. 620] and references

therein for additional information.

350

Some Improperly Posed Cauchy Problems

6.1.3 Example.

The reversed Cauchy problem for the heat equation. Con-

sider the heat equation

ut=1c(U,,+uyy) (6.1.5)

in the square Sl = ((x, y); 0 < x, y < 77) with Dirichlet boundary condition

u = 0 (6.1.6)

on the boundary F. The initial-value problem for (6.1.5), (6.1.6) as an

abstract Cauchy problem in the spaces Cr(S2) and LP(S2), 1 < p < oo was

already examined in Sections 1.1 and 1.3. For the sake of definiteness, we

choose E = Cr(), which is natural if we wish to model a heat propagation

process by means of (6.1.5) (6.1.6). Let t'< T and assume we know the

temperature distribution u at time T,

uT(x, y) = u(x, y, T). (6.1.7)

On the basis of this information, we wish to compute the state of the system

at time t', or more generally, the past states

u(x,y,t)

(t'<t<T).

This reversed Cauchy problem is equivalent (changing t by - t) to the

ordinary Cauchy problem for the equation

ud = - K(uxx + uyy)

(6.1.8)

with boundary condition (6.1.6). Although the reversed Cauchy problem

makes perfect physical sense, it is far from being well posed in the sense of

Section 1.2. It is still true that solutions will exist for a dense set of "final

data" UT; we only have to take UT to be a trigonometric polynomial

M N

UT(x, Y) _ E E amnsin mxsin ny

m=1 n=1

in which case the solution (which is defined for all t) is

M N

u(x, y, t)

E E e-K(m2+n2)(t-T)amnsin mxsin ny

m=1 n=1

(see Section 1.1). However, if we take, say, uT,

(x, y) = sin nx sin ny, we

have I I uT,

11 = 1, but, if un is the corresponding solution,

IIUn(', , t')II =

e2Kn2(T-t')

i 1).

(6.1.9)

This invalidates in practice our model, since small errors in the measure-

ment of uT will foil any attempt at computation of t'). Unlike in the

case of Maxwell's equations (Section 1.6) or the Schrodinger equation

(Section 1.4) in Lp, a "reasonable" renorming of the space of final data will

not help: if we measure UT in, say, the maximum of I UTl and of the modulus

of its derivatives of order < k, I I n -(k+') UT,

l i = n-

I while

Iln-(k+1)un(.,.>t')ll

=n-1e2Kn2(T-Y)

6.1. Improperly Posed Problems

351

This simply means that the Cauchy problem is not even properly posed in

the sense of Hadamard (see Section 1.7). A way out is found, however,

examining more carefully the physical process involved. We add the follow-

ing hypotheses:

(a) The system was in existence at some time t" < t' (we may obvi-

ously assume, by time independence of equation and boundary condition,

that I" = 0).

(b) Ever since the time t" = 0 an a priori bound on the temperature

distribution has been in effect: there exists C > 0 such that

(05t<T),

(6.1.10)

where II'll again indicates the norm of Cr(). We must then eliminate from

consideration every "final state" giving rise to a solution that violates

(6.1.10). It is plain that the class 9 = 6F(T, of "admissible final states"

consists of all UT E Cr(SZ) whose sine Fourier coefficients (amn) satisfy

00 00

m=I n=1

e'(m2+n2)tamnsin

mx sin ny

<C ((x,y)ES2,0<t<T).

(6.1.11)

Although the class Y is not simply characterized, it follows from the

Parseval equality for Fourier series that for any uT E

Iam,,

2Ce-K(m2+n2)T

F-' E ea(m2+n2)(T-t)amnsin

mx sin ny

Let now e > 0 and let UT be an element of Y satisfying I uTI < 6, where 6 is to

be determined later. Then the Fourier coefficients (amn) of uT satisfy

Iamnl < 26.

We have

m=1 n=1

(6.1.12)

(6.1.13)

00 00

E E

eK(m2+n2)(T-t)I

m=I n=1

Dividing the sum in two parts, one corresponding to m, n 5 N, it is easy to

see using (6.1.12) and (6.1.13) that if 6 is sufficiently small we shall have

Iu(x,Y,t)1=

00 00

((x,y)ES2,t'<t<T)

Iu(x,Y,1)1 <E

so that a problem which is in some sense properly posed is obtained. It

should be noted that the misbehavior of the model has not been eliminated,

since the condition that UT E F remains highly unstable with respect to

perturbations. However, numerical methods for treatment of the problem

are available (see the references in Section 6.6).

352

Some Improperly Posed Cauchy Problems

We note, finally, that the two assumptions (a) and (b) are reasonable,

even indispensable in our model: (a) is (almost) necessary for the reversed

Cauchy problem to make sense, while (b) must hold in any heat propagation

process with C (at the very least) the melting point of the material in

question. Hence, the difficulties pointed out at the beginning of this

example can be blamed not on improper modeling but on the neglect of

available information.

6.1.4 Example. An incomplete Cauchy problem for the Laplace equation.

In the theory of probability, equations of the form u,r = - Au appear, with

A an elliptic differential operator in a domain St c R m satisfying adequate

boundary conditions (see Balakrishnan [1958: 1]); the spaces indicated for

the treatment are L'(SZ) and C(F2) or subspaces thereof. To fix ideas, we

examine the equation

urn_-(u"+U.10 (6.1.14)

in the square 9 = ((x, y); 0 < x, y < 7), with Dirichlet boundary condition

u=0 (xEI'). (6.1.15)

Consider two arbitrary trigonometric polynomials

uo (x, y)

a'. sin mx sin ny, u 1(x, y) a' , sin mx sin ny.

The function

00 00

u(x,y,t)

(cosh(m2+n2)112t)amnsinmxsinny

m=1 n=1

°c

(sinh(m2+n2)'"2t)

+ E E i

a;nnsin mxsin ny

m=1 n=1

(m2+n2)

(6.1.16)

is a solution of (6.1.14), (6.1.15) satisfying the initial conditions

u(x,y,0)=uo(x,Y), u'(x,Y,0)=u1(x,Y)

However, the solution does not depend continuously on its initial data. To

see this we take uo, n = n-(k+')sin nxsin ny (which tends to zero uniformly in

SZ together with its partial derivatives of order < k), u1, n = 0, and note that

the corresponding solution is u(x, y, t) = (n-(k+1)coshVnt)sin nxsin ny. In

fact, this is essentially the celebrated counterexample given by Hadamard

[1923: 1] in relation to his formulation of properly posed problems (see the

comments in Section 1.7). However, the subsidiary conditions imposed on

the solutions of (6.1.14), (6.1.15) by their probabilistic interpretation are not

both initial conditions u0, u1, but rather only one of them,

u(x, y,0) = uo(x, y), (6.1.17)

6.1. Improperly Posed Problems 353

and the boundedness condition

(6.1.18)

t>0

(a third requirement is also present, see Balakrishnan [1958: 11, but we leave

it aside for simplicity). This "incomplete Cauchy problem" is easily analyzed

along the lines of Section 1.3; to simplify, we take E = L'(S2). If A denotes

the operator defined in Section 1.3 (with K = 1) and t -. u(., , t) solves the

equation

u"(t)+Au(t)=O (t>,0), (6.1.19)

a calculation entirely similar to (1.3.4) shows that the Fourier series of

u(x, y, t) (for t fixed) must have the form (6.1.16). If we assume in addition

that

supllu(t)II <cc,

(6.1.20)

t>0

the same sort of argument reveals that a;,,n = -(m2 + n2)'/2a°,n, so that

- (m2+n2)1/2t 0

u(x, y, t) - e a,,,nsin mxsin ny. (6.1.21)

n=1 m=1

Among other things, this shows that bounded solutions of (6.1.19) are

uniquely determined by their initial value

u (0) = u0. (6.1.22)

On the other hand, it is easily checked that the series on the right-hand side

of (6.1.21) converges and defines a E-valued solution of (6.1.19) satisfying

(6.1.20) and (6.1.22) for any u0 in the subspace D C L'(Sl) consisting of all

functions whose Fourier coefficients (ao,,) satisfy

00 00

(m2+n2)Iamnl <oo.

m=I n=l

If u is an arbitrary solution, we can write

(6.1.23)

u(x,y,t)= (6.1.24)

where

4 2

2 1,2

K(x,

e -

( +n)

t > 0. The function u(x, y, t) is a classical solution of the Laplace

equation uxx + uyy + utt = 0 in SZ X (0, oo) and tends to zero uniformly when

t - + oo. Arguing as in Section 1.3, but this time on the basis of the

maximum principle for harmonic functions, we can easily show that

K(x, (t> 0, (x, (6.1.26)

354

Some Improperly Posed Cauchy Problems

and

(t>0,(x,y)ESl), (6.1.27)

hence (see (1.3.11)) if is an arbitrary solution of (6.1.19), (6.1.20),

Ilu(t)II < Ilu(0)II

(t , o).

(6.1.28)

Similar inequalities can be easily obtained in the norms of LP(0) and

Cr(Q).

Taking these facts as motivation, we formulate the following incom-

plete Cauchy problem. Let A be a densely defined operator in a (real or

complex) Banach space E. The incomplete Cauchy problem for (6.1.19) is

properly posed in t > 0 if and only if:

(a) There exists a dense subspace D of E such that, for any uo E D

there exists a solution of (6.1.19) satisfying (6.1.20) and

(6.1.22). (A solution is of course any twice continuously differen-

tiable E-valued function satisfying the equation in t >_ 0.)

(b) There exists a nondecreasing, nonnegative function C(t) defined in

t > 0 such that

Ilu(t)II<C(t)Ilu(0)II

(t,0)

for any solution of(6.1.19), (6.1.20), (6.1.22).

Sufficient conditions on the operator A insuring validity of (a) and

(b) will be given in Section 6.5. Many variants of this basic definition are

possible: (6.1.20) may be replaced by other types of bound at infinity, u'(0)

may be preassigned instead of u(0), and so on. Some of these will be

mentioned in Section 6.6.

6.1.5

Example.

Let A be a self-adjoint operator in a Hilbert space H.

Assume - A is positive definite ((Au, u) < 0 for u E D(A)). Then the

incomplete Cauchy problem for (6.1.19) is properly posed in t >, 0 with

D = D(A). Using the functional calculus (see Section 6), we can easily

deduce an explicit formula for the solutions: if u E D(A), the (unique)

solution of (6.1.19), (6.1.20), (6.1.22) is

u(t) =

where P(dX) is the resolution of the identity associated with A.

6.2. THE REVERSED CAUCHY PROBLEM FOR

ABSTRACT PARABOLIC EQUATIONS

It was pointed out in the previous section (Example 6.1.3) that if A is the

Laplacian in the space Cr(SZ), 9 the square defined by 0< x, y < 7r, then the

6.2. The Reversed Cauchy Problem for Abstract Parabolic Equations

355

Cauchy problem for the equation

u'(t)=Au(t) (0<t<T) (6.2.1)

with the value of u prescribed at t = T,

u(T) = uT (6.2.2)

is in general not properly posed (the solution of (6.2.1), (6.2.2), if it exists at

all, does not depend continuously on UT); however, a well-posed problem

results if we restrict our attention to solutions satisfying the a priori bound

Ilu(t)II <C (0<t<T).

(6.2.3)

We prove here a generalization of this result to operators in the class l

in an

arbitrary Banach space E. To simplify ensuing statements we make the

following definition.

The reversed Cauchy problem for (6.2.1) is properly posed for bounded

solutions in 0 < t < T if and only if: for every s, C, t' such that E, C > 0 and

0 < t' < T there exists S = 8(e, C, t') > 0 such that if u(.) is any solution of

(6.2.1) satisfying (6.2.3) and

Ilu(T)II <8,

(6.2.4)

we have

Ilu(t)II<e

(t'<t<T). (6.2.5)

6.2.1 Theorem. Let A E d. Then the reversed Cauchy problem for

(6.2.1) is properly posed for bounded solutions.

For the proof we shall use some elementary results on E-valued

analytic functions. Let S2 be a bounded domain in C whose boundary F

consists of the union of a finite number of disjoint smooth arcs,' and let r,

be a subset of r such that both r, and r\r, are themselves finite unions of

disjoint smooth arcs. The function w(z, r,; 2), which is harmonic in SZ and

assumes the values I on r 0 on r\r is called the harmonic measure of r,

with respect to 2. If r is the union of disjoint arcs,

r = r, u r2 u

urn, (6.2.6)

where each r; satisfies the conditions imposed earlier on r,, it is obvious

that

E w(z,rj,St)=1

(zEn) (6.2.7)

l=I

since the left-hand side is a harmonic function that is identically I on r. A

generalization of (6.2.7) is

4Here "disjoint"

means "having no points other than endpoints in common" or, in

other words, "having disjoint interiors." A smooth arc is by definition the continuously

differentiable image of a closed interval.

356

Some Improperly Posed Cauchy Problems

6.2.2 The N Constants Theorem.

Let I's , I'2, ... , I'n be as in the

comments preceding (6.2.6). Let f be a E-valued function, analytic in Sl and

continuous in l(i.5 Assume that

IIf(z)II<Mj

(zEI..,j=1,2,...,n). (6.2.8)

Then

IIf(z)II < II Mjw (z,r,;'2)

(z E SZ).

(6.2.9)

J=1

The proof can be achieved by applying the n constants theorem for

complex-valued functions (see Nevanlinna [ 1936: 1, p. 411 or Hille [ 1962: 1,

p. 409]) to the function K f(z), u*) for all u* E E*, Ilu*II <1. Details are left

to the reader.

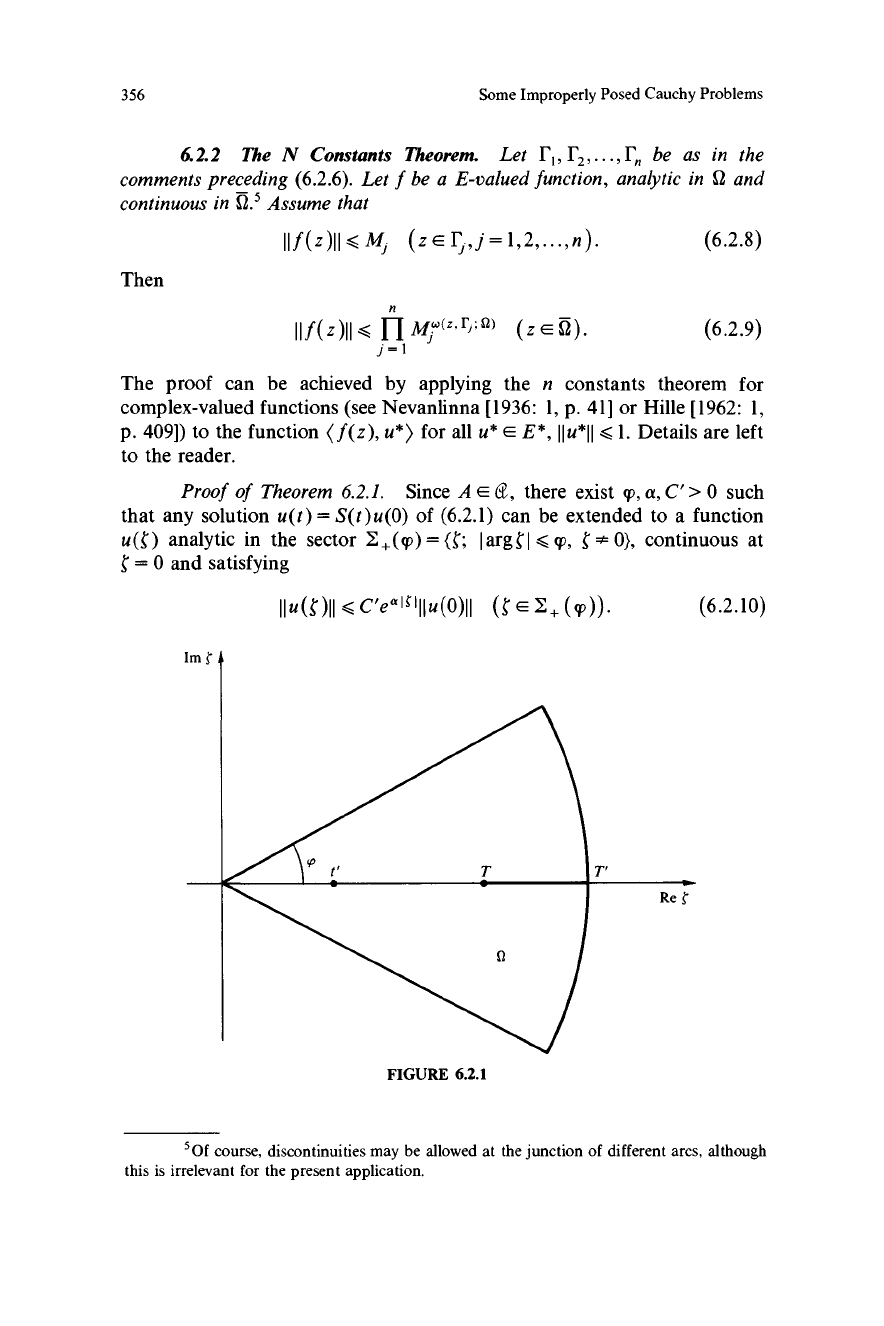
Proof of Theorem 6.2.1.

Since A E d, there exist T, a, C' > 0 such

that any solution u(t) = S(t) u(0) of (6.2.1) can be extended to a function

analytic in the sector I, ((p)

arg

< q2,

0), continuous at

= 0 and satisfying

(6.2.10)

FIGURE 6.2.1

5Of course, discontinuities may be allowed at the junction of different arcs, although

this is irrelevant for the present application.